
OPTIMAL DESIGN OF VARIABLE STRUCTURE LOAD
FREQUENCY CONTROLLER WITH NONLINEARITIES USING
TABU SEARCH ALGORITHM
Naji A. Al-Musabi, Hussain N. Al-Duwaish, A. Mantawy, Zakariya M. Al-Hamouz, Samir Al-Baiyat
King Fahd University of Petroleum and Minerals,Dhahran, Saudia Arabia
Keywords: Variable Structure Control (VSC), Load Frequency Control (LFC), Tabu Search (TS) algorithm
Abstract: This paper discusses the optimal design of Variable Structure Controller (VSC) applied to the Load
Frequency Control (LFC) problem. The controller was designed by an optimal method that utilizes Tabu
Search (TS) algorithm. The proposed method has been applied to a single nonreheat area model that
includes nonlinearities in the form of Generation Rate Constraint (GRC) and governor deadband backlash.
The proposed optimal design was compared with other design methods reported in the literature and showed
improved robust dynamical behavior.
1 INTRODUCTION
The Load Frequency Control (LFC) or Automatic
Generation Control (AGC) has been one of the most
important subjects concerning power system
engineers in the last two decades. Extensive study of
the problem was reported in literature (Fosha &
Elgerd 1970, Elgerd 1971, Nanda & Kaul 1978,
Chan & Hsu 1981, Sivaramakrishanan et. al 1984,
Kumar et. al 1985, Pan & Lian 1989, Das et. al
1991, Beufays et. al 1994, Ha 1998, Al-Hamouz &
Al-Duwaish 2000, Ming-Sheng 2000, Demiroren et.
al 2001, Ryu et. al 2001, Al-Musabi et. al 2003). The
purpose of the LFC is to track the load variation
while maintaining both system frequency and tie-
line power interchanges close to specified values.
Various techniques were utilized in designing the
secondary control loops of LFC. These techniques
include PI and PID methods (Elgerd 1971, Nanda &
Kaul 1978, Moon et. Al 1999, Ryu et. al 2001),
Optimal control (Fosha & Elgerd 1970), Adaptive
control (Pan & Lian 1989), and Neural network
methods (Beufays et. al 1994, Demiroren et. al
2001) . Furthermore, the application of Variable
Structure Control (VSC) to the LFC problem was
investigated by a number of authors (Chan & Hsu
1981, Sivaramakrishanan et. al 1984, Kumar et. al
1985, Das et. al 1991, Ming-Sheng 2000, Ha 1998,
Al-Hamouz & Al-Duwaish 2000, Al-Musabi et. al
2003). Chan and Hsu (1981) designed a VSC
controller and compared it with conventional and
optimal control methods for two equal-area
nonreheat and reheat thermal systems. There study
confirmed the superior performance of VSC over
conventional and optimal control methods.
However, a systematic method for obtaining the
switching vectors and optimum feedback gain
settings were not discussed. Moreover,
Sivaramakrishanan et. al (1984) utilized pole
placement in designing the VSC for a single
nonreheat LFC system. However, optimum gain
settings were not suggested by the authors. Two area
nonreheat and reheat thermal systems were studied
by Kumar et. al (1985) and Das et. al (1991). The
former utilized simple control logic to switch
between proportional and integral controllers
excluding sliding modes. Das et. al (1991) used the
same control logic to switch between VSC and
simple Integral controller. Parameters of the
controllers were optimized using Integral Squared
Error (ISE) technique. Improvement in the
dynamical response of the LFC system was achieved
in comparison to conventional Integral controller.
Using an approximating control law and a new
switching function with integral action, a robust load
frequency controller was designed by Ming-Sheng
(2000). Ming-Sheng method was claimed to reduce
chattering effect of VSC and ensure existence of
sliding mode. However, the author did not show the
behaviour of the control effort. Also, the frequency
response of the designed controller showed
questionable response with the presence of
Generation Rate Constraint (GRC). Applying stricter
GRC was shown to give better dynamic response,
although it is known that a harsher GRC on rate of
27
Al-musabi N., Al-Duwaish H., Mantawy A., Al-Hamouz Z. and Al-Baiyat S. (2004).
OPTIMAL DESIGN OF VARIABLE STRUCTURE LOAD FREQUENCY CONTROLLER WITH NONLINEARITIES USING TABU SEARCH ALGORITHM.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 27-32
DOI: 10.5220/0001142000270032
Copyright
c
SciTePress

generation will cause more degradation in the
performance of the controller. Furthermore, Ha
(1998) proposed a combination of fuzzy, equivalent,
and switching control in designing a robust sliding
mode LFC. Simulations of the system showed both
improved dynamic performance and reduced
chattering.
This paper explores the optimal design of VSC
for the LFC problem using the TS algorithm. It is
considered an extension of the work by Al-Hamouz
and Al-Duwaish (2000) and Al-Musabi et. al (2003),
where the parameters of the VSC controller were
optimized using GA and PSO methods respectively.
However, previously only the feedback gains were
optimized. The switching vector of the controller
was obtained from other design methods. In this
paper, both the switching vector and switching
feedback gains of the VSC are designed optimally
using TS. Moreover, the proposed design of VSC is
applied to LFC models that incorporate the effect of
nonlinearities. The organization of the paper will be
as follows: First, an explanation of the LFC model
will be presented followed by a brief theory of VSC.
Tabu Search algorithm will then be overviewed
followed by a description of the proposed optimal
design procedure. Finally, comparison with other
design methods reported in the literature will be
investigated in the Simulation section.
2 LFC MODEL
The model of a single nonreheat LFC area is shown
in Figure 1(a) (Sivaramakrishanan et. al 1984, Ha
1998). The dynamic model in state variable form can
be obtained from the transfer function model and is
given as
)t(Fd)t(Bu)t(AXX ++=
&
(1)
Where X is a 4-dimensional state vector, u is 1-
dimensional control force vector, d is 1-dimensional
disturbance vector, A is 4x4 input matrix, and F is
4x1 disturbance matrix.
A =
−
−
−−−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
1
00
0
11
0
1
0
11
00 0
T
K
T
TT
RT T T
K
p
p
p
tt
ggg
B
=
T
00
1
0
T
g
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
F
T
= [K
p
/T
p
0 0 0]
T
p
is the plant model time constant, T
t
is the
turbine time constant, T
g
is the governor time
constant, K
p
is the plant gain, K is the integral
control gain, and R is the speed regulation due to
governor action. x
2
, x
3
, and x
4
are respectively the
incremental changes in generator output (p.u. MW) ,
governor valve position (p.u. MW) and integral
control. The control objective in the LFC problem is
to keep the change in frequency (Hz)
∆
ω
= x
1
as
close to zero as possible when the system is
subjected to a load disturbance d by manipulating
the input u.
In this study, nonlinearities will be included in
the LFC models. Figure 1(a) shows these
nonlinearities in the form of limits to the position of
governor valve and the rate of its change. It also
includes the governor deadband backlash. The dead
band of the speed governor is defined as “the
magnitude of the change in steady-state speed within
which there is no resulting change in the position of
the governor-controlled valves or gates” (IEEE
Standard, 1992).
3 VSC THEORY
The fundamental theory of variable structure
systems may be found in (Itkis, 1976). A block
diagram of the VSC is shown in Figure 1(b), where
the control law is a linear state feedback whose
coefficients are piecewise constant functions.
Consider the linear time-invariant controllable
system given by
&
X
A
XBU
=
+
(2)
Where X is n-dimensional state vector, U is m-
dimensional control force vector, A is a n x n system
matrix, and B is n x m input matrix. The VSC
control laws for the system of (2) are given by
∑
=
=−=−=
n
j
jij
T
ii
mixXu
1
,....,2,1;
ψψ
(3)
where the feedback gains are given as
⎪
⎩
⎪
⎨
⎧
=〈−
=〉
=
njxif
mixif
jiij
jiij
ij
,....,1;0,
,....,1;0,
σα
σα
ψ
and
σ
ii
T
XCX i( ) , ,....,== =01m
where C
i
are the switching vectors which are
determined usually via a pole placement technique.
The design procedure for selecting the constant
switching vector C
i
may be found in
(Sivaramakrishanan, 1984).
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
28

4 TABU SEARCH ALGORITHM
Tabu Search Algorithm was proposed a few years
ago by Fred Glover (Glover, 1989) as a general
iterative heuristic method for solving combinatorial
optimization problems. TS is conceptually simple
and elegant heuristic method.
The basic elements of TS are defined as follows:
- Current Solution: x
current
: it is a set of solutions
from which new trial values are generated.
- Moves: the process of generating trial solutions
from x
current
.
- Candidate Moves: it is a set of trial solutions,
x
trial,
generated from neighbourhood of x
current
.
- Tabu list: a list of forbidden moves that
exceeded conditions imposed on moves in general.
- Aspiration Criterion: a device that override the
tabu status of a move. There are different types of
aspiration criteria used in literature (Glover, 1989,
Glover, 1990, Glover & Laguna 1997). The criteria
used here is to override the tabu status of a move if it
produces a better solution than the best solution,
x
best
, seen so far.
- Stopping Criteria: these are the conditions that
terminate the search process. In this study, the
search process will stop when the number of
iterations reaches the maximum limit or if there is no
more improvement for the last 50 iterations. The
Tabu Search algorithm can be described as follows:
Step 1: Generate Random initial solution, x
initial
.
Set x
best
= x
initial
= x
current
.
Step 2: Trial solutions are generated randomly in
the neighborhood of the current solution.
Step 3: The objective function for trial solutions
is computed and compared to best solution objective
function value. If better solution is obtained then x
best
= x
trial
and then Step 4 follows. Otherwise, go to Step
4 directly.
Step 4: Tabu Status of x
trial
is tested. If it is not
in the Tabu list, then add it to the list and set x
current
=
x
trial
and go to Step 7. If x
trial
is in the Tabu list, go to
Step 5.
Step 5: The Aspiration criterion is checked. If
the criterion is satisfied, then the tabu status is
overridden, aspiration is updated, x
current
= x
trial
and
step 7 follows. Otherwise, Step 6 follows.
Step 6: Check all the trial solutions by going
back to Step 4. If all trial solutions are assessed, go
to Step 7.
Step 7: Check the Stopping criterion. If satisfied,
then stop. Otherwise, go to Step 2 for the next
iteration.
5 OPTIMAL DESIGN
PROCEDURE
The VSC for the LFC will be designed optimally as
follows:
1) Generate random values for feedback gains
and switching vector values.
2) Evaluate a performance index that reflects the
objective of the design. In this study the following
objective functions were used:
∫
∞
=
0
2
1
dtJ
ω∆
(4)
∫
+=
0
2
2
2
12
dtuqqJ
∆ω∆
∞
(5)
J
1
minimizes the deviation in fequency. J
2
includes a scaled value of the deviation in the
control effort to reduce the chattering. The effect of
inclusion of this value and a comparison of different
objective functions for different scaling factors q
1
and q
2
may be found in (Al-Musabi et. al, 2004).
3) Use TS to generate new feedback gains and
switching vector values as described in section 4.
4) Evaluate the performance index in step 2 for
the new feedback gains and switching vector. Stop if
there is no more improvement in the value of the
performance index for the last 50 iterations or if the
maximum number of iterations is reached; otherwise
go to step 3.
6 SIMULATION RESULTS
CASE I: In this case comparison with a robust
controller design (Wang et. al, 1993) is investigated.
The following are the parameters of the system:
1/T
p
= 0.0665 1/RT
g
= 6.86
1/T
t
= 3.663 K
p
/T
p
= 8
1/T
g
= 13.736 K = 0.6
A GRC of 0.1 p.u. MW per minute = 0.0017 p.u.
MW/sec was included in the model. The limits were
also applied to integral control signal. The system
was simulated for a 0.01 p.u. load disturbance.
The design procedure described in section 5 was
applied to the system with performance index of
equation (5) applied with q
1
= q
2
=1. The optimal
setting for VSC in this case is obtained as follows:
C = [1.6384 28.9077 9.3736 6.8697]
α
= [0.2616 0.3022 0.8951 0.0335]
The convergence of the performance index and
the dynamical behaviour of the system is shown in
Figure 2.
OPTIMAL DESIGN OF VARIABLE STRUCTURE LOAD FREQUENCY CONTROLLER WITH NONLINEARITIES
USING TABU SEARCH ALGORITHM
29

CASE II: In this case, the design method of Ha
(1998) was compared with the new proposed design
method. The parameters of the studied system are
given below (Ha, 1998) :
T
p
= 20 s K
p
= 120 Hz p.u.MW
-1
T
t
= 0.3 s K = 0.6 p.u. MW rad
-1
T
g
= 0.08 s R = 2.4 Hz p.u. MW
-1
A backlash of 2D = 0.001 and generation limits
= 0.1 p.u.MW/min and
max
.
P
=
max
P∆
0.03
p.u.MW are applied. The system was simulated
for a load disturbance of 0.005 p.u.MW
The design procedure described in section 5 was
again applied to the system with the performance
index of equation (4) applied. The optimal settings
of the VSC are given below. The system response is
shown in Figure 3.
C = [14.8804 37.3156 47.5501 2.9652]
α
= [3.3792 4.7826 4.4277 0.5580]
Figure 1: (a) Single area LFC with nonlinearities (b) Block diagram of Variable Structure controller
(a) (b)
X
C
T
−
α
T
α
T
σ
X
σ
ψ
T
UX
T
=−
ψ
g
T
1
s
1
t
sT+1
1
P
P
sT
K
+1
s
K
R
1
-
-
Figure 2: Case I: (a) Convergence of performance index (b) Frequency deviation (c) Frequency deviation: for a 25%
change in parameters (d) Control effort
(a)
(
b
)
(c)
(d)
L
P
∆
max
P
&
max
P∆
Governor
Backlash
2D
+
- -
-
-
Rate limits
Position
limits
x
1
x
2
x
3
x
4
Load
Disturbance
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
30
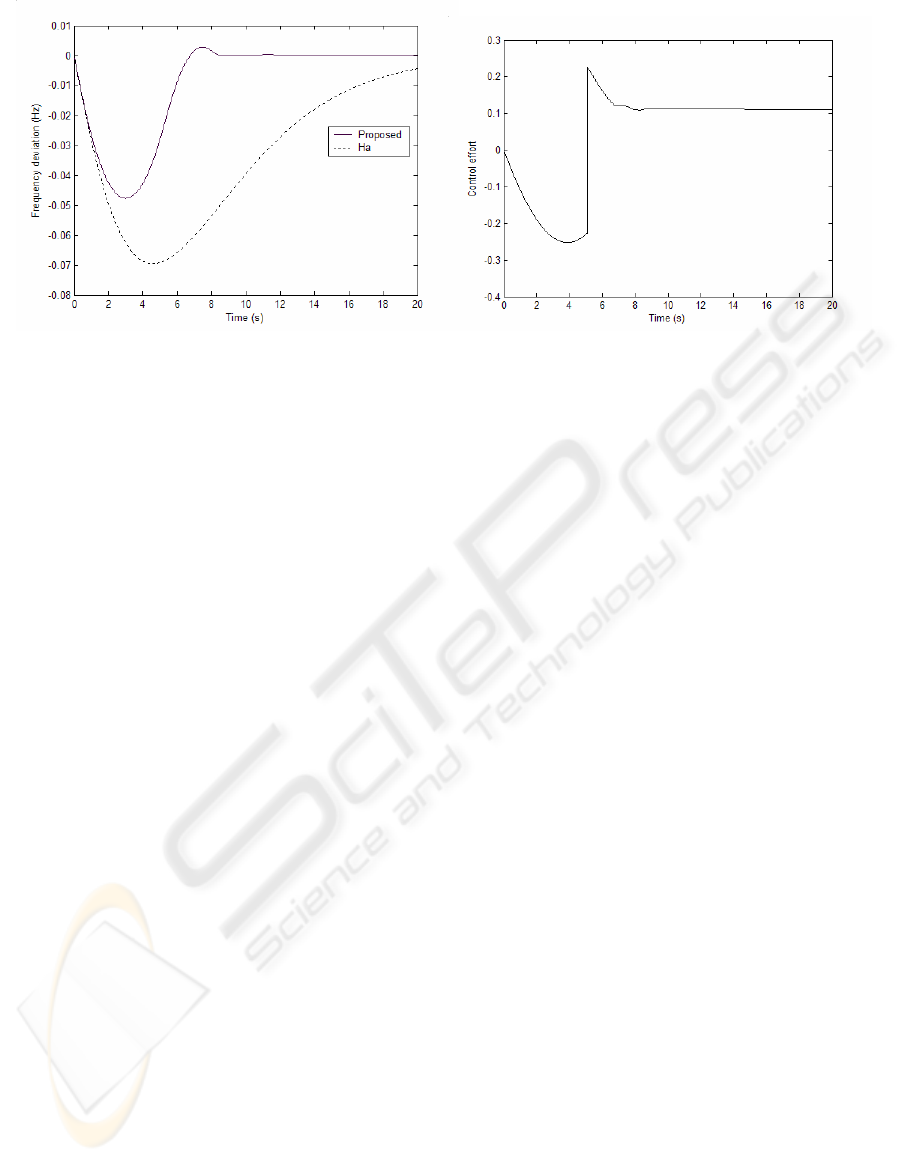
The following can be concluded from the above
results: lts:
1) The new optimal design of VSC using TS
algorithm improves the dynamical
behavior of the LFC system when
compared with other design methods
reported in literature. This is depicted in
Figures 2(b) and 3(a).
1) The new optimal design of VSC using TS
algorithm improves the dynamical
behavior of the LFC system when
compared with other design methods
reported in literature. This is depicted in
Figures 2(b) and 3(a).
2) A smooth control effort is obtained. This
is shown in Figures 2(d) and 3(b).
Inclusion of the deviation in the control
effort into the objective function, equation
(5), reduced the chattering in the VSC.
2) A smooth control effort is obtained. This
is shown in Figures 2(d) and 3(b).
Inclusion of the deviation in the control
effort into the objective function, equation
(5), reduced the chattering in the VSC.
3) The proposed VSC showed a robust
behavior, Figure 2(c).
3) The proposed VSC showed a robust
behavior, Figure 2(c).
4) Nonlinearities can be easily included into
the studied model. In this paper, the
proposed VSC was applied to LFC models
with governor deadband and GRC
nonlinearities.
4) Nonlinearities can be easily included into
the studied model. In this paper, the
proposed VSC was applied to LFC models
with governor deadband and GRC
nonlinearities.
7 CONCLUSION 7 CONCLUSION
In this paper, Tabu Search algorithm was used in the
optimal design of VSC applied to the load frequency
control problem. A robust controller with smooth
control signal was designed efficiently for a single
area LFC system that incorporates nonlinearities.
Comparison with other reported design methods
showed promising results and an improvement in the
dynamical behaviour of the LFC system.
In this paper, Tabu Search algorithm was used in the
optimal design of VSC applied to the load frequency
control problem. A robust controller with smooth
control signal was designed efficiently for a single
area LFC system that incorporates nonlinearities.
Comparison with other reported design methods
showed promising results and an improvement in the
dynamical behaviour of the LFC system.
ACKNOWLEDGEMENT ACKNOWLEDGEMENT
The authors would like to acknowledge the support
of King Fahd university of Petroleum and Minerals.
The authors would like to acknowledge the support
of King Fahd university of Petroleum and Minerals.
REFERENCES REFERENCES
Elgerd, O. I., 1971, Electric Engergy System Theory: An
Introduction, McGraw-Hill, USA.
Elgerd, O. I., 1971, Electric Engergy System Theory: An
Introduction, McGraw-Hill, USA.
Nanda, J., B. L. Kaul, 1978, Automatic Generation control
of an Interconnected Power System, IEE Proc., vol.
125, no. 5, pp. 385-390
Nanda, J., B. L. Kaul, 1978, Automatic Generation control
of an Interconnected Power System, IEE Proc., vol.
125, no. 5, pp. 385-390
Moon, Y.-H., Ryu, H.-S., Choi, B.-K., Cho, B.-H., 1999,
Modified PID Load-Frequency Control with
consideration of valve position limits, Proc. of IEEE
PES Winter Meeting, vol.1, pp. 701-706.
Moon, Y.-H., Ryu, H.-S., Choi, B.-K., Cho, B.-H., 1999,
Modified PID Load-Frequency Control with
consideration of valve position limits, Proc. of IEEE
PES Winter Meeting, vol.1, pp. 701-706.
Ryu, H.-S., Jung, K.-Y., Park, J.-D., Moon, Y.-H., Rhew,
H.-W., 2001, Extended Integral control for load-
Frequency Control with the consideration of
generation rate constraint, IEEE PES Winter Meeting,
vol.3, pp. 1289-1293.
Ryu, H.-S., Jung, K.-Y., Park, J.-D., Moon, Y.-H., Rhew,
H.-W., 2001, Extended Integral control for load-
Frequency Control with the consideration of
generation rate constraint, IEEE PES Winter Meeting,
vol.3, pp. 1289-1293.
Fosha, C. E. and Elgerd, O. I., 1970, The Megawatt-
Frequency control problem: A new approach via
optimal control theory, IEEE Trans. Power Appar.
and Syst., vol. PAS-89, pp. 563-577
.
Fosha, C. E. and Elgerd, O. I., 1970, The Megawatt-
Frequency control problem: A new approach via
optimal control theory, IEEE Trans. Power Appar.
and Syst., vol. PAS-89, pp. 563-577
.
Pan, C. T. and Lian, C. M., 1989, An adaptive controller
for power system load frequency control, IEEE Trans.
on Power Systems, vol. 4, no.1, pp. 122-128.
Pan, C. T. and Lian, C. M., 1989, An adaptive controller
for power system load frequency control, IEEE Trans.
on Power Systems, vol. 4, no.1, pp. 122-128.
Beufays, F., Magid, Y. A., Widrow, B., 1994,
Applications of Neural Networks to load frequency
control in power systems, Neural Networks, vol.7,
no.1, pp. 183-194.
Beufays, F., Magid, Y. A., Widrow, B., 1994,
Applications of Neural Networks to load frequency
control in power systems, Neural Networks, vol.7,
no.1, pp. 183-194.
Demiroren, A., N. S. Semgor, Zeynelgil, H. L., 2001,
Automatic generation control by using ANN
technique, Electric Power Components and Systems,
vol. 29, no.10, pp. 883-896.
Demiroren, A., N. S. Semgor, Zeynelgil, H. L., 2001,
Automatic generation control by using ANN
technique, Electric Power Components and Systems,
vol. 29, no.10, pp. 883-896.
Figure 3: Case II: (a) Frequency deviation (b) Control effort
(b)
(a)
OPTIMAL DESIGN OF VARIABLE STRUCTURE LOAD FREQUENCY CONTROLLER WITH NONLINEARITIES
USING TABU SEARCH ALGORITHM
31

Chan, W. C. and Hsu, Y. Y., 1981, Automatic generation
control of interconnected power system using variable
structure controller, IEE Proc. Part C, vol. 128, no. 5,
pp. 269-279.
Sivaramakrishanan, A. Y., M. V. Hariharan, M. V., M. C.
Srisailam, M. C., 1984, Design of variable structure
load frequency controller using pole assignment
technique, Int. Journal Control, vol. 40, no.3, pp. 487-
498.
Kumar, A., Malik, O. P., Hope, G. S., 1985, Variable
structure system control applied to AGC of an
interconnected power systems, IEE Proc. Pt. C, vol.
132, no.1, pp. 23-29.
Das, D., Kothari, M. L., Kothari, D. P., Nanda, J., 1991,
Variable structure control strategy to automatic
generation control of interconnected reheat thermal
system, IEE Proc Pt. D, vol. 138, no. 6, pp. 579-585.
Ming-Sheng, Y., 2000, Load frequency scheme for power
systems using smoothed switching structure theory,
Proc. IEEE International Symposium on Industrial
Electronics, vol. 1, pp. 191-195.
Ha, Q. P., A Fuzzy sliding mode controller for power
system load frequency control, 1998, Second
International Conference on Knowledge-Based
Intelligent Electronic Systems, vol. 1, pp. 149-154.
Al-Hamouz, Z. and Al-Duwaish, H., 2000, A new load
frequency variable structure controller using Genetic
Algorithms, Electric Power Systems Research, vol. 55,
pp. 1-6.
Al-Musabi, N. A., Al-Hamouz, Z. M., Al-Duwaish, H. N.,
Al-Baiyat, S., 2003, Variable structure load frequency
controller using Particle Swarm Optimization
technique, Proc. of the 10
IEEE International
Conference on Electronics, Circuits and Systems, pp.
380-383.
th
IEEE Standard 122-1991, Recommended practice for
functional and performance characteristics of control
systems for steam turbine-generator units, 1992.
Itkis, 1976, Control systems of variable structure, Keter
Publishing House, Jerusalem.
Glover, F., 1989, Tabu Search-Part I, ORSA Journal on
Computing, vol. 1, No. 3, pp. 190-206.
Glover, F., 1990, Tabu Search-Part II, ORSA Journal on
Computing, vol. 2, No. 1, pp. 4-32.
Glover, F., and Laguna, M., 1997, Tabu Search, Kluwer
Academic Publisher, Boston.
Al-Musabi, N. A., Al-Duwaish, H. N., Al-Hamouz, Z. M.,
Al-Baiyat, S., 2004, Variable structure load frequency
controller: Optimal design and chattering reduction
using particle swarm optimization algorithm, Accepted
in 9
th
International conference on optimization of
electrical and electronic equipment.
Wang, Y., Zhou, R., Wen, C., 1993, Robust load-
frequency controller design for power systems, IEE.
Proc. C, vol. 140, pp. 11-16.
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
32
