
MOMENT-LINEAR STOCHASTIC SYSTEMS
Sandip Roy
Washington State University, Pullman, WA
George C. Verghese
Massachusetts Institute of Technology, Cambridge, MA
Bernard C. Lesieutre
Lawrence Berkeley National Laboratory, Berkeley, CA
Keywords:
jump-linear systems, linear state estimation and control, stochastic network models
Abstract:
We introduce a class of quasi-linear models for stochastic dynamics, called moment-linear stochastic systems
(MLSS). We formulate MLSS and analyze their dynamics, as well as discussing common stochastic models
that can be represented as MLSS. Further studies, including development of optimal estimators and controllers,
are summarized. We discuss the reformulation of a common stochastic hybrid system—the Markovian jump-
linear system (MJLS)—as an MLSS, and show that the MLSS formulation can be used to develop some
new analyses for MJLS. Finally, we briefly discuss the use of MLSS in modeling certain stochastic network
dynamics. Our studies suggest that MLSS hold promise in providing a framework for modeling interesting
stochastic dynamics in a tractable manner.
1 INTRODUCTION
As critical networked infrastructures such as air traffic
systems, electric power systems, and communication
networks have become more interdependent, the need
for models for large-scale and hybrid network dynam-
ics has grown. While the dramatic improvement in
computer processing speeds in recent years has some-
times facilitated predictive simulation of these net-
works’ dynamics, the development of models that al-
low not only prediction of dynamics but also network
control and design remains a challenge in several ap-
plication areas (see, e.g., (Bose, 2003)). In this article,
we introduce and give the basic analysis for a class
of models called moment-linear stochastic systems
(MLSS) that can represent some interesting stochas-
tic and hybrid system/network dynamics, and yet
are sufficiently structured to allow computationally-
attractive analyses of dynamics, state estimation, and
control. Our studies suggest that MLSS hold promise
as a modeling tool for a variety of stochastic and
hybrid dynamics, especially because they provide a
framework for several common stochastic and/or hy-
brid models in the literature, and because they can
capture some network dynamics in a tractable man-
ner.
Our research is partially concerned with hybrid
(mixed continuous- and discrete-state) dynamics.
Stochastic hybrid models whose dynamics are con-
strained to Markovian switching between a finite
number of linear time-invariant models have been
studied in detail, under several names (e.g., Marko-
vian jump-linear systems (MJLS) and linear jump-
Markov systems) (Loparo et al., 1991; Mazor et al.,
1998). Techniques for analyzing the dynamics of
MJLS, and for developing estimators and controllers,
are well-known (e.g., (Fang and Loparo, 2002; Costa,
1994; Mazor et al., 1998)). Of particular interest to us,
a linear minimum-mean-square error (LMMSE) esti-
mator for the continuous state of an MJLS was devel-
oped by (Costa, 1994), and quadratic controllers have
been developed by, e.g., (Chizeck and Ji, 1988). We
will show that similar estimation and control analyses
can be developed for MLSS, and hence can be applied
to a wider range of stochastic dynamics.
We are also interested in modeling stochastic net-
work interactions. There is wide literature on stochas-
tic network models that is largely beyond the scope of
this article. Of particular interest to us, several mod-
els from the literature on queueing and stochastic au-
tomata can be viewed as stochastic hybrid networks
(see (Kelly, 1979; Rothman and Zaleski, 1997; Dur-
rett, 1981) for a few examples). By and large, the
aims of the analyses for these models differ from our
aims, in that transient dynamics are not characterized,
and estimators and controllers are not developed. One
190
Roy S., Verghese G. and Lesieutre B. (2004).
MOMENT-LINEAR STOCHASTIC SYSTEMS.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 190-197
DOI: 10.5220/0001143401900197
Copyright
c
SciTePress

class of stochastic automata of particular interest to
us are Hybrid Bayesian Networks (e.g., (Heskes and
Zoeter, 2003)). These are graphical models (i.e., mod-
els in which stochastic interactions are specified using
edges on a graph) with hybrid (i.e., mixed continuous-
state and discrete-state) nodal variables. Dynamic
analysis, inference (estimation), and parameter learn-
ing have been considered for such networks, but com-
putationally feasible methods are approximate.
We observe that stochastic systems models with
certain linear or quasi-linear structures (e.g., linear
systems driven by additive white Gaussian noise,
MJLS) are often widely tractable: statistics of tran-
sient dynamics can be analyzed, and LMMSE esti-
mators and optimal quadratic controllers can be con-
structed. Several stochastic network models with
quasi-linear interaction structures have also been
proposed—examples include the voter model or inva-
sion process (Durrett, 1981), and our influence model
(Asavathiratham, 2000). For these network models,
the quasi-linear structure permits partial characteriza-
tion of state occupancy probabilities using low-order
recursions. In this article, we view these various lin-
ear and quasi-linear models as examples of moment-
linear models—i.e., models in which successive mo-
ments of the state at particular times can be inferred
from equal and lower moments at previous times us-
ing linear recursions. This common representation
for quasi-linear system and network dynamics moti-
vates our formulation of MLSS, which are similarly
tractable to the examples listed above. The MLSS
formulation is further useful, in that it suggests some
new analyses for particular examples and elucidates
some other types of stochastic interactions that can be
tractably modeled.
The remainder of the article is organized as fol-
lows: in Section 2, we describe the formulation and
basic analysis—namely, the recursive computation of
state statistics—of MLSS. We also list common mod-
els, and types of stochastic interactions, that can be
captured using MLSS. Section 3 contains a summary
of further results on MLSS. In Section 4, we refor-
mulate the MJLS as an MLSS, and apply the MLSS
analyses to this model. We also list other common hy-
brid models that can be modeled as MLSS. Section 5
summarizes our studies on using MLSS to model net-
work dynamics. In this context, a discrete-time flow
network model is developed in some detail.
2 MLSS: FORMULATION AND
BASIC ANALYSIS
An MLSS is a discrete-time Markov model in which
the conditional distribution for the next state given
the current state is specially constrained at each time-
step. These conditional distributions are constrained
so that successive moments and cross-moments of
state variables at each time-step can be found as lin-
ear functions of equal and lower moments and cross-
moments of state variables at the previous time-step,
and hence can be found recursively.
Formally, consider a discrete-time Markov process
with an m-component real state vector. The state (i.e.,
state vector) of the process at time k is denoted by
s[k]. We write {s[k]} to represent the state sequence
s[0], s[1], . . . and s
i
[k] to denote the ith element of
the state vector at time k. We stress that we do not
in general enforce any structure on the state variables,
other than that they be real; the state vector may be
continuous-valued, discrete-valued, or hybrid.
For this Markov process, we consider the con-
ditional expectation E(s[k + 1]
⊗r
| s[k]), for r =
1, 2, . . ., where the notation s[k + 1]
⊗r
refers to the
Kronecker product of the vector s[k + 1] with it-
self r times and is termed the rth-order state vec-
tor at time k. This expectation vector contains all
rth moments and cross-moments of the state variables
s
1
[k + 1], . . . , s
n
[k + 1] given s[k], and so we call the
vector the conditional rth (vector) moment for s[k+1]
given s[k]. We say that the process {s[k]} is rth-
moment linear at time k if the conditional rth moment
for s[k + 1] given s[k] can be written as follows:
E(s[k + 1]
⊗r
| s[k]) = H
r,0
[k] +
r
X
i=1
H
r,i
[k]s[k]
⊗i
,
(1)
for some set of matrices H
r,0
[k], . . . , H
r,r
[k].
The Markov process {s[k]} is called a moment-
linear stochastic system (MLSS) of degree br if it is
rth-moment linear for all r ≤ br, and for all times
k. If a Markov model is moment linear for all r and
k, we simply call the model an MLSS. We call the
constraint (1) the rth-moment linearity condition at
time k, and call the matrices H
r,0
[k], . . . , H
r,r
[k] the
rth-moment recursion matrices at time k. These re-
cursion matrices feature prominently in our analysis
of the temporal evolution of MLSS.
MLSS are amenable to analysis, in that we can find
statistics of the state s[k] (i.e., moments and cross-
moments of state variables) using linear recursions.
In particular, for an MLSS of degree br, E(s[k + 1]
⊗r
)
(called the rth moment of s[k + 1]) can be found in
terms of the first r moments of s[k] for any r ≤ br. To
find these rth moments, we use the law of iterated ex-
pectations and then invoke the rth-moment linearity
MOMENT-LINEAR STOCHASTIC SYSTEMS
191

condition:
E(s[k + 1]
⊗r
) = E(E(s[k + 1]
⊗r
| s[k])) (2)
= E(H
r,0
[k] +
r
X
i=1
H
r,i
[k]s[k]
⊗i
)
= H
r,0
[k] +
r
X
i=1
H
r,i
[k]E(s[k]
⊗i
).
We call (2) the rth-moment recursion at time k. Con-
sidering equations of the form (2), we see that the first
r moments of s[k + 1] can be found as a linear func-
tion of the first r moments of s[k]. Thus, by applying
the moment recursions iteratively, the rth moment of
s[k] can be written in terms of the first r moments of
the initial state s[0].
The recursions developed in equations of the
form (2) can be rewritten in a more concise form,
by stacking rth and lower moment vectors into a
single vector. In particular, defining s
0
(r)
[k] =
£
s
0
[k]
⊗r
. . . s
0
[k]
⊗1
1
¤
, we find that
E(s
(r)
[k + 1]) =
˜
H
(r)
[k]E(s
(r)
[k]), (3)
where
˜
H
(r)
[k] = (4)
H
r,r
[k] H
r,r−1
[k] . . . H
r,1
[k] H
r,0
[k]
0 H
r−1,r−1
[k] . . . H
r−1,1
[k] H
r−1,0
[k]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 . . . 0 H
1,1
[k] H
1,0
[k]
0 . . . 0 0 1
.
Interactions and Examples Captured by MLSS
MLSS provide a convenient framework for represent-
ing several models that are prevalent in the literature.
These MLSS reformulations are valuable in that they
expose similarity in the moment structure of several
types of stochastic interactions, and in that they per-
mit new analyses (e.g., development of linear state es-
timators, or characterization of higher moments) in
the context of these examples. Common models that
can be represented as MLSS are listed:
• A linear system driven by independent, identically
distributed noise samples with known statistics is
an MLSS.
• A finite-state Markov chain can be formulated as
an MLSS, by defining the MLSS state to be a 0–1
indicator vector of the state of the Markov chain.
• An MJLS is a hybrid model that can be reformu-
lated as an MLSS. This reformulation of an MJLS
is described in Section 4.
• A Markov-modulated Poisson process (MMPP) is
a stochastic model that has commonly been used
to represent sources in communications and man-
ufacturing systems (e.g., (Baiocchi et al., 1991),
(Nagarajan et al., 1991), (Ching, 1997)). It con-
sists of a finite-state underlying Markov chain, as
well as a Poisson arrival process with (stochastic)
rate modulated by the underlying chain. An MMPP
can be formulated as an MLSS using a state vector
the indicates the underlying Markov chain’s state
and also tracks the number of arrivals over time
(see (Roy, 2003) for details). The MLSS refor-
mulation of MMPPs highlights that certain state-
parametrized stochastic updates, such as a Pois-
son generator with mean specified as a linear func-
tion of the current state, can be represented using
MLSS. More generally, various stochastic updates
with state-dependent noise can be represented.
• Certain infinite server queues can be represented as
MLSS (see (Roy, 2003) for details).
Observations and Inputs Observations and exter-
nal inputs are naturally incorporated in MLSS. These
are structured so as to preserve the moment-linear
structure of the dynamics, and hence to allow devel-
opment of recursive linear estimators and controllers
for MLSS.
At each time k, we observe a real vector z[k] that
is independent of the past history of the system, (i.e.,
s[0], . . . , s[k − 1] and z[0], . . . , z[k − 1]), given the
current state s[k]. The observation z[k] is assumed to
be first- and second-moment linear given s[k]. That
is, z[k] is generated from s[k] in such a way that the
first moment (mean) for z[k] given s[k] can be written
as an affine function of s[k]:
E(z[k] | s[k]) = C
1,1
s[k] + C
1,0
(5)
for some C
1,1
and C
1,0
, and the second moment for
z[k] given s[k] can be written as an affine function of
s[k] and s[k]
⊗2
:
E(z[k]
⊗2
| s[k]) = C
2,2
s[k]
⊗2
+C
2,1
s[k]+C
2,0
(6)
for some C
2,2
, C
2,1
, and C
2,0
.
We have restricted observations to a form for which
analytical expressions for LMMSE estimators can be
found, yet relevant stochastic interactions that are not
purely linear can be captured. Observation gener-
ation from the state in MLSS admits the same va-
riety of stochastic interactions—e.g., linear interac-
tions, finite-state Markovian transitions, certain state-
parameterized stochastic updates—as captured by the
MLSS state update. This generality allows us to
model, e.g., Hidden Markov Model observations (Ra-
biner, 1986), random selection among multiple lin-
ear observations, and observations of a Poisson arrival
process with mean modulated by the state.
The inputs in our model are structured in such a
way that the next state is first- and second-moment
linear with respect to both the current state and the
current input. Specifically, a system is a 2nd-degree
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
192

MLSS with state sequence {s[k]} and input {u[k]}
if the conditional distribution for the next state is in-
dependent of the past history of the system, given
the current state and input, and if there exist matri-
ces H
1,1
, D
1,1
, H
1,0
, H
2,2
, G
2,2
, D
2,2
, H
2,1
, D
2,1
,
and H
2,0
such that
E(s[k +1] | s[k], u[k]) = H
1,1
s[k]+D
1,1
u[k]+H
1,0
and
E(s[k + 1]
⊗2
| s[k], u[k])
= H
2,2
s[k]
⊗2
+ G
2,2
(s[k] ⊗ u[k]) + D
2,2
u[k]
⊗2
+H
2,1
s[k] + D
2,1
u[k] + H
2,0
. (7)
That is, a Markov process is a 2nd-degree MLSS with
input u[k] if the first and second moments and cross-
moments of the next state, given the current state and
input, are first- and second-degree polynomials, re-
spectively, of current state and input variables.
We have restricted MLSS inputs to a form for
which analytical expressions for optimal quadratic
controllers can be found, yet several relevant types
of input interactions can nevertherless be represented.
The dependence of the state on the input has the same
generality as the state update.
3 FURTHER RESULTS
In the following paragraphs, we summarize four re-
sults on MLSS that are elaborated further in (Roy,
2003).
Cross Moments Cross-moments of state variables
across multiple time-steps can be calculated, by re-
cursively rewriting cross-moments across time-steps
as linear functions of moments and cross-moments at
single times. Our expressions for cross-moments are
similar in flavor to the Kronecker product-based ex-
pressions for higher-order statistics of linear systems
given by, e.g., (Mendel, 1975; Swami and Mendel,
1990), but apply to MLSS.
Asymptotics We develop necessary and sufficient
conditions for convergence (approach to a steady-
state value) of MLSS moments
1
in (Roy, 2003). Con-
ditions for moment convergence are useful because
they can help to characterize asymptotic dynamics:
they can in some instances be used to prove conver-
gence of the state itself, or to prove distributional con-
vergence, for example.
Because the moments satisfy linear recursions,
conditions for convergence can straightforwardly be
1
Our study of moment convergence is limited to the state
update of an MLSS; input-output stability has not yet been
considered.
expressed in terms of the modes of the moment recur-
sion matrices. However, we note that redundancy in
the moment vectors, which is inherent to the MLSS
formulation, complicates development of good con-
vergence conditions because it allows introduction of
spurious unstable modes that do not actually alter the
moments. We therefore develop reduced forms of the
moment recursions to construct the necessary and suf-
ficient conditions for moment convergence. Details
are in (Roy, 2003).
Estimation We have developed a recursive al-
gorithm for linear minimum mean square error
(LMMSE) filtering of MLSS. Because tractability of
estimation and control is a primary goal in our formu-
lation of MLSS, it is worthwhile for us to present our
estimator, and to connect it to related literature.
Our LMMSE filter for an MLSS is a generalization
of the discrete-time Kalman filter (see, e.g., (Catlin,
1989)), in which the state update and observation pro-
cesses are constrained to be moment-linear rather than
purely linear. Equivalently, we can view our filter as
applying to a linear system in which certain quasi-
linear state-dependence of state and observation noise
is permitted. From this viewpoint, our filter is re-
lated to the LMMSE filter introduced in (Zehnwirth,
1988), which allows for state-dependent observation
variance. Also of interest to us are linear estima-
tion techniques for arrival processes whose under-
lying rate processes are themselves random, and/or
arrival-dependent (e.g., (Snyder, 1972),(Segall et al.,
1975)). Segall and Kailath describe a broad class of
arrival processes of this type, for which a martingale
formulation facilitates nonlinear recursive estimation
(Segall et al., 1975). We also can capture some ar-
rival processes with stochastic rates (e.g., MMPPs),
and hence develop recursive state estimators for these
processes. The arrival processes that are MLSS are a
subset of those in (Segall et al., 1975), but for which
linear filtering is possible, and hence exact finite-
dimensional estimators can be constructed.
The derivation of our LMMSE filter for MLSS,
which closely follows the derivation of the discrete-
time Kalman filter, can be found in (Roy, 2003).
Here, we only present the results of our analysis.
We use the following notation: we define
b
s
k|k
as
the LMMSE estimate for s[k] given z[0], . . . , z[k],
and define Σ
k|k
4
= E
¡
(s[k] −
b
s
k|k
)(s[k] −
b
s
k|k
)
0
¢
as the error covariance of this estimate. Also, we
define
b
s
k+1|k
as the LMMSE estimate for s[k +
1] given z[0], . . . , z[k], and let define Σ
k+1|k
4
=
E
¡
(s[k + 1] −
b
s
k+1|k
)(s[k + 1] −
b
s
k|k
)
0
¢
as the er-
ror covariance of this estimate.
As with the Kalman filter, the estimates are found
recursively, in two steps. First, a next-state update is
MOMENT-LINEAR STOCHASTIC SYSTEMS
193

used to determine
b
s
k+1|k
and Σ
k|k
in terms of
b
s
k|k
,
Σ
k|k
, and the a priori statistics of s[k]. The next-state
update for our filter is
b
s
k+1|k
= H
1,1
b
s
k|k
+ H
1,0
(8)
Σ
k+1|k
= H
1,1
Σ
k|k
H
0
1,1
+ M
k
(E(s[k], E(s[k]
⊗2
)) (9)
In (9), M
k
(E(s[k], E(s[k]
⊗2
)) is the (a priori) expec-
tation for the conditional variance of z[k] given s[k];
an explicit expression is given in (Roy, 2003).
Second, a measurement update is used to determine
b
s
k|k
and Σ
k|k
in terms of z[k],
b
s
k|k−1
, Σ
k|k−1
, and the
a priori statistics of s[k]. The measurement update for
our filter is
b
s
k|k
=
b
s
k|k−1
+ Σ
k|k−1
C
0
1,1
(C
1,1
Σ
k|k−1
C
0
1,1
+
N
k
(E(s[k], E(s[k]
⊗2
)))
−1
(z[k] − C
1,1
b
s
k|k−1
− C
1,0
)
Σ
k|k
= Σ
k|k−1
−
Σ
k|k−1
C
0
1,1
(C
1,1
Σ
k|k−1
C
0
1,1
+
N
k
¡
E(s[k]), E(s[k]
⊗2
)
¢
)
−1
C
1,1
Σ
k|k−1
. (10)
In (10), N
k
¡
E(s[k]), E(s[k]
⊗2
)
¢
is the a priori ex-
pectation for the conditional variation of s[k+1] given
s[k]; an explicit expression is given in (Roy, 2003).
Control Considering the duality between linear es-
timation and quadratic control, it is not surprising that
optimal dynamic quadratic control can be achieved
for MLSS, given full state information. In (Roy,
2003), we use a dynamic programming formulation
for the quadratic control problem to find a closed-
form recursion for the optimal control. The optimal
control at each time is linear with respect to the cur-
rent state, in analogy to the optimal quadratic control
for a linear system. The reader is referred to (Roy,
2003) for presentation and discussion of the optimal
controller, as well as a description of relevant litera-
ture.
4 EXAMPLE: MJLS
We describe the reformulation of MJLS as MLSS,
and then present some analyses of MJLS using the
MLSS formulation. For simplicity, we only detail
the reformulation of a Markovian jump-linear state-
update equation here; reformulation of the entire
input-output dynamics is a straightforward extension.
Let’s consider the update equation
x[k + 1] = A(q[k])x[k] + b
k
(q[k]), (11)
where {q[k]} is a 0–1 indicator vector sequence rep-
resentation for an underlying Markov chain with fi-
nite state-space. We denote the transition matrix for
the underlying Markov chain by Θ = [θ
ij
]. We de-
note the number of components of x[k] as n, and the
number of statuses in the underlying Markov chain as
m.
For convenience, we rewrite (11) in an extended
form as
˜x[k + 1] =
˜
A(q[k])˜x[k], (12)
where ˜x[k] =
·
x[k]
1
¸
and
˜
A(q[k]) =
·
A(q[k]) b(q[k])
0 1
¸
.
To reformulate the jump-linear system as an MLSS,
we define a state vector that captures both the con-
tinuous state and underlying Markov dynamics of the
jump-linear system. In particular, we define the state
vector as s[k] = q[k] ⊗ ˜x[k], and consider the first
conditional vector moment E(s[k + 1] | s[k]). Since
s[k] uniquely specifies x[k] and q[k], we can deter-
mine this first conditional vector moment as follows:
E(s[k + 1] | s[k]) = E(s[k + 1] | q[k], x[k])(13)
= E(q[k + 1] ⊗ ˜x[k + 1] | x[k], q[k])
= E(q[k + 1] | q[k]) ⊗
˜
A(q[k])˜x[k]
= Θ
0
q[k] ⊗
˜
A(q[k])˜x[k]
With a little bit of algebra, we can rewrite Equation
13 as
E(s[k + 1] | s[k]) = (14)
θ
11
˜
A(q[k] = e(1)) . . . θ
m1
˜
A(q[k] = e(m))
.
.
.
.
.
.
.
.
.
θ
1m
˜
A(q[k] = e(1)) . . . θ
mm
˜
A(q[k] = e(n))
s[k],
where e(i) is an indicator vector with the ith entry
equal to 1.
Equation (14) shows that the first-moment lin-
earity condition holds for {s[k]}. To justify that
higher-moment linearity conditions hold, let’s con-
sider entries of the rth-conditional moment vec-
tor E(s[k + 1]
⊗r
| s[k]) = E((q[k + 1] ⊗ ˜x[k +
1])
⊗r
| x[k], q[k]). Because q[k] is an indicator, the
non-zero entries of the rth-conditional moment vector
can all be written in the form E(q
i
[k +1]
Q
n
i=1
x
i
[k +
1]
α
i
| x[k], q[k]), where each α
i
≥ 0, and
P
n
i=1
α
i
=
br ≤ r. Given that q[k] = e(i), 1 ≤ i ≤ m,
E(
Q
n
i=1
x
i
[k+1]
α
i
| x[k], q[k]) is an brth degree poly-
nomial of x
1
[k], . . . , x
n
[k], say p
i
[k]. Using that
q[k] is an indicator vector, we can rewrite E(q
i
[k +
1]
Q
n
i=1
x
i
[k + 1]
α
i
| x[k], q[k]) as
P
m
i=1
q
i
[k]p
i
[k].
Hence, we see that each entry in the rth-conditional
moment vector is linear with respect to the entries in
s[k]
⊗r
= (q[k + 1] ⊗ ˜x[k + 1])
⊗r
, and so the state
vector is rth-moment linear. Some bookkeeping is
required to express the higher-moment linearity con-
ditions in vector form; these expressions are omitted.
We believe that the MLSS reformulation of MJLS
is valuable, because it places MJLS in the context of a
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
194

broader class of models, and because it facilitates sev-
eral analyses of MJLS dynamics. Some analyses of
MJLS dynamics that can be achieved using the MLSS
formulation are listed below. Our analyses are illus-
trated using an example MJLS with a two-status un-
derlying Markov chain and scalar continuous-valued
state. The underlying Markov chain for this example
has transition matrix Θ =
·
0.9 0.1
0.3 0.7
¸
. The scalar
continuous state is updated as follows: if the Markov
chain is in the first status at time k, then the time-
(k +1) continuous state is x[k + 1] = −0.9x[k]+0.5;
if the Markov chain is in the second status, the time-
(k + 1) continuous state is x[k + 1] = x[k] + 1.
The MLSS formulation allows us to compute
statistics (moments and cross-moments) for both
the continuous-valued state and underlying Markov
status, as well as conditional statistics for the
continuous-valued state given the underlying Markov
status (at one or several times). Recursions for the
first- and second-moments of the continuous-valued
state are well-known (see, e.g., (Costa, 1994)), though
our second-moment recursion differs in form from the
recursion on the covariance matrix that is common in
the literature. We have not seen general computations
of higher-order statistics, or of statistics across time-
steps: the MLSS formulation provides a concise no-
tation in which to develop recursions for these statis-
tics. The higher-moment recursions are especially
valuable because they can provide characterizations
for MJLS asymptotics. We can specify conditions
for δ-moment stability (see, e.g., (Fang et al., 1991))
for all even integer δ in terms of the eigenvalues of
the higher moment recursions. We can also charac-
terize the asymptotics of MJLS in which the state it-
self does not stabilize, by checking for convergence of
moments (to non-zero values). We are currently ex-
ploring whether the methods of (Meyn and Tweedie,
1994) can be used to prove distributional convergence
from moment convergence.
For illustration, first- and second-order statistics
of the example MLSS are shown along with a fifty
time-step simulation in Fig. 1. Additionally, the
steady-state values for the first three moments of the
continuous-valued state have been obtained from the
moment recursions, and are shown along with the cor-
responding steady-state distribution. We note that the
first three moments provide significant information
about the steady-state distribution and, in this exam-
ple, require much less effort to compute than the full
distribution.
The MLSS formulation allows us to develop con-
ditions for moment convergence in MJLS. In (Roy,
2003), we have presented necessary and sufficient
conditions for moment convergence of an MJLS with
scalar continuous-valued state and two-status under-
lying Markov chain, in terms of its parameters. Our
0 5 10 15 20 25 30 35 40 45 50
−10
−5
0
5
10
Continuous−Valued State: Sample Run and Statistics
Time
Sample Run, Mean,
and 2 σ Bounds
0 5 10 15 20 25 30 35 40 45 50
0
0.2
0.4
0.6
0.8
1
Underlying Markov Chain Status
Time
Sample Run and
Prob. of Status "1"
−20 −15 −10 −5 0 5 10 15 20
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
Steady−State Distribution
Continuous−Valued State
Probability Distribution
Mean = 0.92
St. Dev.=3.4
Skewness=3.8
Figure 1: This figure illustrates the MLSS-based analy-
sis of moments for an example MJLS. The top plot in
this figure specifies the continuous-valued state during a 50
time-step simulation, along with the computed mean value
and two standard deviation intervals for this continuous-
valued state. The middle plot indicates the status of the
underlying Markov chain during the simulation and also
shows the probability that the Markov chain is in status “1”.
The bottom plot shows the steady-state distribution for the
continuous-valued state (found through iteration of the dis-
tribution) and lists the moments of this continuous-valued
state (found with much less computation using the moment
recursions).
example MJLS, with statistics shown in Fig. 1, can
be shown to be moment-convergent. Our study of
moment convergence complements stability studies
for MJLS (e.g., (Fang and Loparo, 2002)), by allow-
ing identification of MJLS whose moments reach a
steady-state but that are not stable (in the sense that
state itself does not reach a steady-state).
The MLSS reformulation can be used to develop
LMMSE estimators for MJLS. LMMSE estimation of
the continuous-valued state of an MJLS from noisy
observations has been considered by (Costa, 1994).
The observation structure (i.e., the generator of the
observation from the concurrent state) assumed by
(Costa, 1994) can be captured using our MLSS for-
mulation, and in that case our estimator is nearly iden-
tical to that of (Costa, 1994); only the squared error
that is minimized by the two estimators is slightly dif-
ferent.
MOMENT-LINEAR STOCHASTIC SYSTEMS
195
Our MLSS formulation allows for estimation for a
variety of observation structures. For instance, we can
capture observations that are Poisson random vari-
ables, with parameter equal to a linear function of
the state variables. (Such an observation model may
be realistic, for example, if the state process modu-
lates an observed Poisson arrival process.) We can
also capture other types of state-dependent noise in
the observation process, as well as various discrete
and continuous-valued state-independent noise. Fur-
ther, hybrids of multiple observation structures can be
captured in the MLSS formulation.
Another potential advantage of the MLSS formula-
tion is that, because the underlying Markov status is
part of the state vector, this underlying status can be
estimated. The accuracy of our estimator for the un-
derlying state remains to be assessed. A direction for
future study is to compare our estimator for the un-
derlying status with the nonlinear estimators of, e.g.,
(Sworder et al., 2000; Mazor et al., 1998).
0 5 10 15 20 25 30 35 40 45 50
−8
−6
−4
−2
0
2
4
6
8
10
Time
x[k] and y[k]
Continuous State and Observations
State x[k]
Observation y[k]
0 5 10 15 20 25 30 35 40 45 50
−8
−6
−4
−2
0
2
4
6
8
Time
x[k] and \hat{x}[k]
Continuous State and Estimate
State x[k]
Estimate \hat{x}[k]
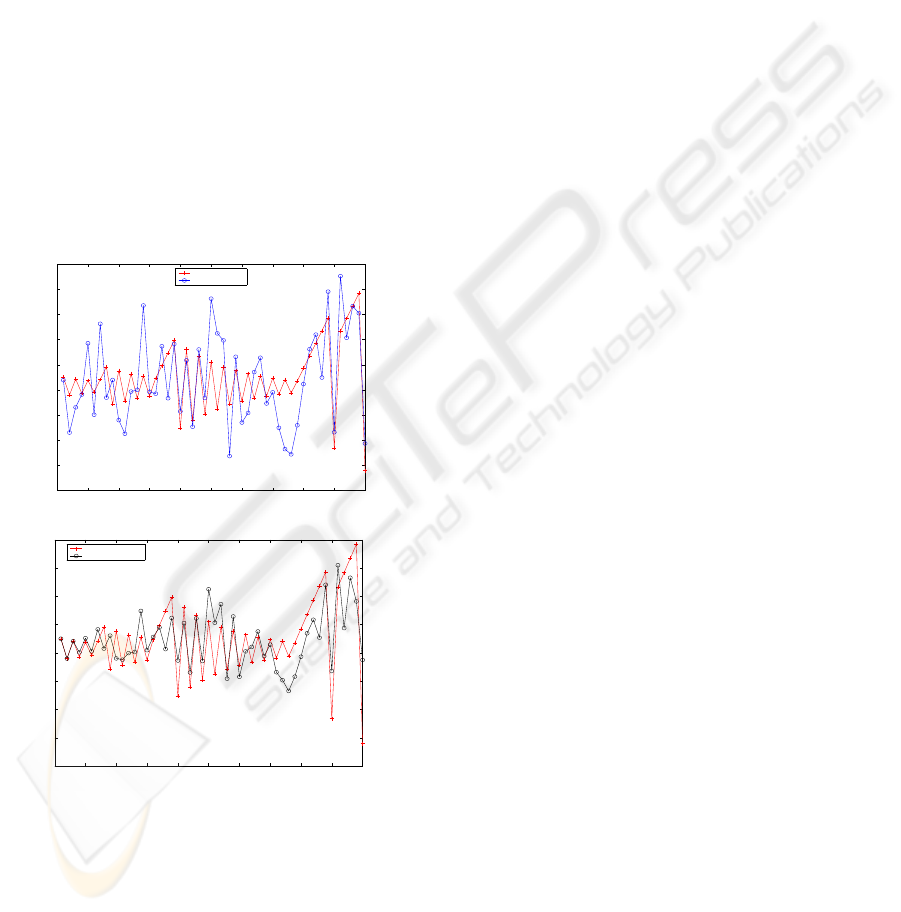
Figure 2: In the left plot, the continuous-valued state and
observations during a 50 time-step simulation of the exam-
ple MJLS are shown. In the right plot, the LMMSE estimate
for the continuous-valued state is compared with the actual
continuous-valued state. The LMMSE estimate is a better
approximation for the continuous-valued state than the ob-
servation sequence.
For illustration, we have developed an LMMSE
filter for our example MJLS. Here, we observe the
(scalar) continuous-valued state upon corruption by
additive white Gaussian noise. Fig. 2 illustrates the
performance of the LMMSE estimator, for a partic-
ular sample run. Our analysis shows that the error
covariance of our estimate is about half the measure-
ment error covariance, verifying that our estimate is
usually a more accurate estimate for the state than the
unfiltered observation sequence.
5 MLSS MODELS FOR
NETWORK DYNAMICS:
SUMMARY
We believe that MLSS representations for networks
are of special interest because analysis of stochastic
network dynamics is quite often computationally in-
tensive (e.g., exponential in the number of vertices),
while MLSS representations can permit analysis at
much lower computational cost. Below, we summa-
rize our studies of MLSS representations for network
dynamics. More detailed description of MLSS mod-
els for network dynamics can be found in (Roy, 2003).
The following are examples of MLSS models for
network dynamics that we have considered.
• The influence model was introduced in (Asavathi-
ratham, 2000) as a network of interacting finite-
state Markov chains, and is developed and mo-
tivated in some detail in (Asavathiratham et al.,
2001). We refer the reader to (Basu et al., 2001)
for one practical application, as a model for con-
versation in a group. The influence model consists
of sites with discrete-valued statuses that evolve in
time through stochastic interaction. The influence
model’s structured stochastic update permits for-
mulation of the model as an MLSS, using 0–1 in-
dicator vector representations for each site’s status.
The rth moment recursion permits computation of
the joint probabilities of the statuses of groups of r
sites, and hence the configurations of small groups
of sites can be characterized using low-order re-
cursions. The MLSS formulation for the influence
model can also be used to develop good state esti-
mators for the model, and to prove certain results
on the convergence of the model.
• MLSS can be used to represent single-server
queueing networks with linear queue length-
dependent arrival and service rates, operating under
heavy-traffic conditions. The MLSS formulation
allows us to find statistics and cross-statistics of the
queue lengths. Of particular interest is the possi-
bility for using the MLSS formulation to develop
queue-length estimators for these state-dependent
models and, indirectly, for Jackson networks (see,
e.g., (Kelly, 1979)).
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
196

• In (Roy et al., 2004), we have developed an MLSS
model for aircraft counts in regions of the U.S.
airspace, and have used the MLSS formulation to
compute statistics of aircraft counts in regions. In
the context of this MLSS model, we have also de-
veloped techniques for parameter estimation from
data.
REFERENCES
Asavathiratham, C. (2000). The Influence Model: A
Tractable Representation for the Dynamics of Net-
worked Markov Chains, Ph.D. Thesis. EECS Depart-
ment, Massachusetts Institute of Technology.
Asavathiratham, C., Roy, S., Lesieutre, B. C., and Verghese,
G. C. (2001). The influence model. IEEE Control
Systems Magazine.
Baiocchi, A., Melazzi, N. B., Listani, M., Roveri, A., and
Winkler, R. (1991). Loss performance analysis of
an ATM multiplexer loaded with high-speed on off
sources. IEEE Journal on Selected Areas of Commu-
nications, 9:388–393.
Basu, S., Choudhury, T., Clarkson, B., and Pentland, A.
(2001). Learning human interactions with the influ-
ence model. MIT Media Lab Vision and Modeling
TR#539.
Bose, A. (2003). Power system stability: new opportuni-
ties for control. Stability and Control of Dynamical
Systems with Applications.
Catlin, D. E. (1989). Estimation, Control, and the Discrete
Kalman Filter. Springer-Verlag, New York.
Ching, W. K. (1997). Markov-modulated Poisson processes
for multi-location inventory problems. International
Journal of Production Economics, 52:217–233.
Chizeck, N. J. and Ji, Y. (1988). Optimal quadratic con-
trol of jump linear systems with Gaussian noise in
discrete-time. Proceedings of the 27th IEEE Confer-
ence on Decision and Control, pages 1989–1999.
Costa, O. L. V. (1994). Linear minimum mean square er-
ror estimation for discrete-time markovian jump lin-
ear systems. IEEE Transactions on Automatic Con-
trol, 39:1685–1689.
Durrett, R. (1981). An introduction to infinite particle sys-
tems. Stochastic Processes and their Applications,
11:109–150.
Fang, Y. and Loparo, K. A. (2002). Stabilization of
continuous-time jump linear systems. IEEE Transac-
tions on Automatic Control, 47:1590–1603.
Fang, Y., Loparo, K. A., and Feng, X. (1991). Modeling is-
sues for the control systems with communication de-
lays. Ford Motor Co., SCP Research Report.
Heskes, T. and Zoeter, O. (2003). Generalized belief propa-
gation for approximate inference in hybrid bayesian
networks. Proceedings of the Ninth International
Workshop on Artificial Intelligence and Statistics.
Kelly, F. P. (1979). Reversibility and Stochastic Networks.
John Wiley and Sons, New York.
Loparo, K. A., Buchner, M. R., and Vasuveda, K. (1991).
Leak detection in an experimental heat exchanger pro-
cess: a multiple model approach. IEEE Transations on
Automatic Control, 36.
Mazor, E., Averbuch, A., Bar-Shalom, Y., and Dayan, J.
(1998). Interacting multiple model methods in target
tracking: a survey. IEEE Transactions on aerospace
and electronic systems, 34(1):103–123.
Mendel, J. M. (1975). Tutorial on higher-order statistics
(spectra) in signal processing and system theory: the-
oretical results and some applications. Proceedings of
the IEEE, 3:278–305.
Meyn, S. and Tweedie, R. (1994). Markov
Chains and Stochastic Stability.
http://black.csl.uiuc.edu/ meyn/pages/TOC.html.
Nagarajan, R., Kurose, J. F., and Towsley, D. (1991). Ap-
proximation techniques for computing packet loss in
finite-buffered voice multiplexers. IEEE Journal on
Selected Areas of Communications, 9:368–377.
Rabiner, L. R. (1986). A tutorial on hidden markov models
and selected applications in speech recognition. Pro-
ceedings of the IEEE, 77(2):257–285.
Rothman, D. and Zaleski, S. (1997). Lattice-Gas Cellular
Automata: Simple Models of Complex Hydrodynam-
ics. Cambridge University Press, New York.
Roy, S. (2003). Moment-Linear Stochastic Systems and
their Applications. EECS Department, Massachusetts
Institute of Technology.
Roy, S., Verghese, G. C., and Lesieutre, B. C. (2004).
Moment-linear stochastic systems and networks. Sub-
mitted to the Hybrid Systems Computation and Con-
trol conference.
Segall, A., Davis, M. H., and Kailath, T. (1975). Nonlinear
filtering with counting observations. IEEE Transac-
tions on Information Theory, IT-21(2).
Snyder, D. L. (1972). Filtering and detection of doubly
stochastic poisson processes. IEEE Transactions on
Information Theory, IT-18:91–102.
Swami, A. and Mendel, J. M. (1990). Time and lag re-
cursive computation of cumulants from a state space
model. IEEE Transactions on Automatic Control,
35:4–17.
Sworder, D. D., Boyd, J. E., and Elliot, R. J. (2000). Modal
estimation in hybrid systems. Journal of Mathemati-
cal Analysis and Applications, 245:225–247.
Zehnwirth, B. (1988). A generalization of the Kalman fil-
ter for models with state-dependent observation vari-
ance. Journal of the American Statistical Association,
83(401):164–167.
MOMENT-LINEAR STOCHASTIC SYSTEMS
197
