
REALISTIC DYNAMIC SIMULATION OF AN INDUSTRIAL ROBOT
WITH JOINT FRICTION
Ronald G.K.M. Aarts, Ben J.B. Jonker
University of Twente, Faculty of Engineering Technology
Enschede, The Netherlands
Rob R. Waiboer
Netherlands Institute for Metals Research
Delft, The Netherlands
Keywords:
Realistic closed-loop trajectory simulation, Industrial robot, Perturbation method, Friction modelling.
Abstract:
This paper presents a realistic dynamic simulation of the closed-loop tip motion of a rigid-link manipulator
with joint friction. The results from two simulation techniques are compared with experimental results. A
six-axis industrial St
¨
aubli robot is modelled. The LuGre friction model is used to account both for the sliding
and pre-sliding regime. The manipulation task implies transferring a laser spot along a straight line with a
trapezoidal velocity profile.
Firstly, a non-linear finite element method is used to formulate the dynamic equations of the manipulator
mechanism. In a closed-loop simulation the driving torques are generated by the control system. The computed
trajectory tracking errors agree well with the experimental results. Unfortunately, the simulation is very time-
consuming due to the small time step of the discrete-time controller.
Secondly, a perturbation method has been applied. In this method the perturbed motion of the manipulator is
modelled as a first-order perturbation of the nominal manipulator motion. Friction torques at the actuator joints
are introduced at the stage of perturbed dynamics. A substantial reduction of the computer time is achieved
without loss of accuracy.
1 INTRODUCTION
Robotic manipulators for laser welding must pro-
vide accurate path tracking performance of 0.1 mm
and less at relatively high tracking speed exceed-
ing 100 mm/s. High speed manipulator motions are
accompanied by high-frequency vibrations of small
magnitudes whereas velocity reversals in the joints
lead to complicated joint friction effects. These dy-
namic phenomena may significantly effect the weld
quality, since laser welding is sensitive to small varia-
tions in the processing conditions like welding speed
as well as to disturbances of the position of the laser
spot with respect to the seam to be welded. To study
the applicability of industrial robotic manipulators as
in Fig. 1 for laser welding tasks, a framework for real-
istic dynamic simulations of the robot motion is being
developed. Such a simulation should predict the path
tracking accuracies, thereby taking into account the
dynamic limitations of the robotic manipulator such
as joint flexibility, friction and limits of the drive sys-
tem like the maximum actuator torques. Obviously
the accuracy of the simulation has to be sufficiently
high with respect to the allowable path deviations.
Unfortunately, closed-loop dynamic simulations
with a sufficient degree of accuracy are computation-
ally expensive and time consuming especially when
static friction, high-frequency elastic modes and a
digital controller operating with small discrete time
steps are involved. In an earlier paper we discussed
a so-called perturbation method (Jonker and Aarts,
2001) which proved to be accurate and computation-
ally efficient for simulations of robotic manipulators
with flexible links. In this paper a similar perturbation
scheme is presented for the closed-loop dynamic sim-
ulation of a rigid-link manipulator with joint friction.
The extension to an industrial robot with elastic joints
is still a topic of ongoing research.
We consider the motion of a six axes industrial
robot (St
¨
aubli RX90B), Fig. 1. The unknown robot
manipulator parameters, such as inertias of the ma-
nipulator arms, the stiffness and the pretension of a
gravity compensation spring are determined by means
of parameter identification techniques. The friction
characteristics are identified separately. The con-
troller model is based on manufacturer’s data and has
been verified experimentally using system identifica-
tion techniques. Details of the identification tech-
48
Aarts R., Jonker B. and Waiboer R. (2004).
REALISTIC DYNAMIC SIMULATION OF AN INDUSTRIAL ROBOT WITH JOINT FRICTION.
In Proceedings of the First Inter national Conference on Informatics in Control, Automation and Robotics, pages 48-55
DOI: 10.5220/0001143500480055
Copyright
c
SciTePress

Axis 1
Axis 2
Axis 3
Axis 4
Axis 5
Axis 6
Figure 1: The six axes St
¨
aubli RX90B Industrial robot
Axis 5
Hinge 1 (q
1
)
Hinge 2 (q
2
)
Hinge 3 (q
3
)
Hinge 4 (q
4
)
Hinge 5 (q
5
)
Hinge 6 (q
6
)
End-effector
Base
Beam 1
Beam 2
Beam 3
Beam 4
Beam 5
Beam 6
Truss 1 (k
s
, σ
(c,0)
)
Figure 2: The 6 DOF Finite Element Model.
niques are outside the scope of this paper and will be
outlined elsewhere (Waiboer, 2004).
The present paper will focus on two simulation
techniques and a comparison of numerical and exper-
imental results. At first, a non-linear finite element
method (Jonker, 1990) is used to formulate the dy-
namic equations of the manipulator mechanism, sec-
tion 2. The finite element formulation and the pro-
posed solution method are implemented in the pro-
gram SPACAR (Jonker and Meijaard, 1990). An inter-
face to MAT LAB is available and the closed-loop sim-
ulations are carried out using SIMULIN K’s graphical
user interface. A driving system is added to the ma-
nipulator model, section 3, and the influence of joint
friction is taken into account, section 4. The LuGre
friction model (Wit et al., 1995) has been used as it
accounts for both the sliding and pre-sliding regimes.
Finally the closed-loop model is assembled by includ-
ing the control system, section 5.
The second approach is the so-called perturbation
method, section 6. The differences between the actual
manipulator motion and the nominal (desired) motion
are modelled as first order perturbations of that nomi-
nal motion. The computation of the perturbed motion
is carried out in two steps. In the first step, the finite
element method permits the generation of locally lin-
earised models (Jonker and Aarts, 2001). In the sec-
ond step, the linearised model can simulate the per-
turbed motion of the manipulator accurately as long
as it remains sufficiently close to the nominal path.
The perturbation method is computationally more ef-
ficient as the non-linear model only has to solved dur-
ing the first step in a limited number of points along
the nominal trajectory. This is the solution of an in-
verse dynamic analysis along a known path, so with
only algebraic equations. The friction torques at the
actuator joints and the control system are introduced
at the stage of perturbed dynamics in the second step.
In section 7, the simulation results will be compared
with the experimental results. Also results acquired
with the perturbation method will be compared with
those obtained from a full non-linear dynamic simu-
lation.
2 FINITE ELEMENT
REPRESENTATION OF THE
MANIPULATOR
In the non-linear finite element method, a manipu-
lator mechanism is modelled as an assembly of fi-
nite elements interconnected by joint elements such
as hinge elements and (slider) truss elements. This
is illustrated in Fig. 2, where the St
¨
aubli robot with
six degrees of freedom is modelled by three different
types of elements. The gravity compensation spring
is modelled as a slider-truss element. The manipu-
lator arms are modelled by beam elements. Finally,
the joints are represented by six cylindrical hinge ele-
ments, which are actuated by torque servos. The ma-
nipulator mechanism is assembled by allowing the el-
ements to have nodal points in common. The con-
figuration of the manipulator is then described by the
vector of nodal coordinates x, some of which may
be the Cartesian coordinates, while others describe
the orientation of orthogonal triads rigidly attached
at the element nodes. The motion of the manipulator
mechanism is described by relative degrees of free-
dom which are the actuator joint angles denoted by
the vector q. By means of the geometric transfer func-
tions F
(x)
and F
(e,c)
, the nodal coordinates x and the
elongation of the gravity compensating spring e
(c)
are
expressed as functions of the joint angles q
x = F
(x)
(q) (1)
and
e
(c)
= F
(e,c)
(q) . (2)
REALISTIC DYNAMIC SIMULATION OF AN INDUSTRIAL ROBOT WITH JOINT FRICTION
49

Differentiating the transfer functions with respect to
time gives
˙
x = DF
(x)
˙
q (3)
and
˙e
(c)
= DF
(e,c)
˙
q, (4)
where the differentiation operator D represents partial
differentiation with respect to the degrees of freedom.
The acceleration vector
¨
x is obtained by differentiat-
ing (3) again with respect to time,
¨
x = DF
(x)
¨
q + (D
2
F
(x)
˙
q)
˙
q. (5)
The geometric transfer functions F
(x)
and F
(e,c)
are
determined numerically in an iterative way (Jonker,
1990).
The inertia properties of the concentrated and dis-
tributed mass of the elements are described with the
aid of lumped mass matrices. Let M(x) be the global
mass matrix, obtained by assembling the mass matri-
ces of the individual elements and let f (x,
˙
x, t) be
the global force vector including gravity forces and
the velocity dependent inertia forces. Then the equa-
tions of motion described in the dynamic degrees of
freedom are given by
¯
M
¨
q + DF
(x)T
h
M(D
2
F
(x)
˙
q)
˙
q − f
i
+ DF
(e,c)T
σ
(c)
= τ ,
(6)
where
¯
M = DF
(x)T
MDF
(x)
is the reduced mass
matrix and σ
(c)
is the total stress in the gravity com-
pensating spring. The vector τ represents the joint
driving torques. The constitutive relation for the grav-
ity compensating spring is described by
σ
(c)
= σ
(c,0)
+ k
s
e
(c)
, (7)
where σ
c,0
and k
s
denote the pre-stress and the stiff-
ness coefficients of the spring, respectively.
This finite element method has been implemented
in the SPACAR software program (Jonker and Mei-
jaard, 1990).
3 THE DRIVING SYSTEM
The robot is driven by servo motors connected via
gear boxes to the robot joints. The inputs for the drive
system are the servo currents i
j
and the outputs are the
joint torques τ
j
, where the subscript j = 1..6 denotes
either the motor or the joint number. A schematic
model of the drives of joints 1 to 4 is shown in Fig. 3.
The relations between the vector of motor angles ϕ,
the vector of joint angles q and their time derivatives
are given by
ϕ = Tq, (8)
˙
ϕ = T
˙
q, (9)
¨
ϕ = T
¨
q, (10)
q
j
c
(m)
j
ϕ
j
J
(m)
j
n
j
i
j
τ
j
τ
(f )
j
Figure 3: Schematic representation of the drives for joints 1
to 4.
where T is the transmission model for the joints. For
joints j = 1..5 only the respective gear ratio n
j
of the
joint plays a role. The drives for the wrist of the robot,
drives 5 and 6, are coupled. This causes an extra term
leading to
T =
n
1
0 0 0 0 0
0 n
2
0 0 0 0
0 0 n
3
0 0 0
0 0 0 n
4
0 0
0 0 0 0 n
5
0
0 0 0 0 n
6
n
6
. (11)
The friction torque in each joint is denoted τ
(f)
j
with
j = 1..6. Due to the coupling in the wrist, an addi-
tional friction torque τ
(f)
7
is identified on the axis of
motor 6. The vector of joint friction torques is then
defined as
τ
(f)
=
h
τ
(f)
1
, τ
(f)
2
, τ
(f)
3
, τ
(f)
4
, · · ·
τ
(f)
5
+τ
(f)
7
, τ
(f)
6
+τ
(f)
7
i
T
.
(12)
The joint friction modelling is continued in section 4.
The drives are equipped with permanent magnet,
three-phase synchronous motors, yielding a linear re-
lation between motor currents and torque. The vector
of joint driving torques τ is then given by
τ = T
T
C
(m)
i − T
T
J
(m)
¨
ϕ − τ
(f)
, (13)
where the matrices C
(m)
and J
(m)
are diagonal ma-
trices with the motor constants c
(m)
j
and rotor inertias
J
(m)
j
, respectively. Substitution of (10) and (13) into
(6) and some rearranging yields
¯
M
(n)
¨
q + DF
(x)T
h
M(D
2
F
(x)
˙
q)
˙
q − f
i
+ DF
(e,c)T
σ
(c)
= τ
(n)
,
(14)
where the mass matrix
¯
M
(n)
is defined by
¯
M
(n)
=
¯
M + T
T
J
(m)
T , (15)
as the rotor inertias T
T
J
(m)
T obviously have to be
added to the reduced mass matrix
¯
M in the equations
of motion (6). Furthermore, the vector of net joint
torques is defined as
τ
(n)
= T
T
C
(m)
i − τ
(f)
. (16)
The inertia properties and spring coefficients have
been found by means of parameter identification tech-
niques (Waiboer, 2004).
ICINCO 2004 - ROBOTICS AND AUTOMATION
50

4 JOINT FRICTION MODEL
For feed-forward dynamic compensation purposes
and robot inertia identification techniques it is com-
mon to model friction in robot joints as a torque τ
(f)
which consists of a Coulomb friction torque and an
additional viscous friction torque for non-zero veloc-
ities (Swevers et al., 1996; Calafiore et al., 2001).
These so-called static or kinematic friction models
are valid only at sufficiently high velocities because
they ignore the presliding regime. At zero velocity
they show a discontinuity in the friction torque which
gives rise to numerical integration problems in a for-
ward dynamic simulation. To avoid this problem we
apply the LuGre friction model (Wit et al., 1995), that
accounts for both the friction in the sliding and in the
presliding regime.
In the LuGre friction model there is an internal state
z that describes the average presliding displacement,
as introduced by Heassig et al. (Haessig and Fried-
land, 1991). The state equations with a differential
equation for the state z and an output equation for the
friction moment τ
(f)
are
˙z = ˙q −
| ˙q |
g( ˙q)
z, (17)
τ
(f)
= c
(0)
z + c
(1)
˙z + c
(2)
˙q . (18)
Note that a subscript j = 1 . . . 7 should be added to all
variables to distinguish between the separate friction
torques in the robot model, but it is omitted here for
better readability. For each joint friction model with
j = 1..6 the input velocity equals the joint velocity ˙q
j
.
For the extra friction model τ
(f)
7
the input velocity is
defined as the sum of the joint velocities of joints 5
and 6.
In general, the friction torque in the pre-sliding
regime is described by a non-linear spring-damper
system that is modelled with an equivalent stiffness
c
(0)
for the position–torque relationship at velocity re-
versal and a micro-viscous damping coefficient c
(1)
.
At zero velocity, the deformation of the non-linear
spring torque is related to the joint (micro) rotation
q.
The viscous friction torque in the sliding regime is
modelled by c
(2)
˙q, where c
(2)
is the viscous friction
coefficient. In addition, at a non-zero constant veloc-
ity ˙q, the internal state z, so the average deformation,
will approach a steady state value equal to c
(0)
g( ˙q).
The function g( ˙q) can be any function that represents
the constant velocity behaviour in the sliding regime.
In this paper the Stribeck model will be used, which
models the development of a lubricating film between
the contact surfaces as the relative velocity increases
from zero. The Stribeck model is given by
c
(0)
g( ˙q) = τ
(c)
+ (τ
(s)
− τ
(c)
)e
−(| ˙q|/ω
s
)
δ
, (19)
where τ
(c)
is known as Coulomb friction torque, τ
(s)
is the static friction torque and ω
s
and δ are shaping
parameters. The values for the static friction torque
τ
(s)
and Coulomb friction torque τ
(c)
may be differ-
ent for positive and negative velocities and are there-
fore distinguished by the subscripts + and −, respec-
tively.
For each friction torque in the robot model, the
parameters describing the sliding regime of the Lu-
Gre friction model are estimated separately using
dedicated joint torque measurements combined with
non-linear parameter optimisation techniques (Wai-
boer, 2004). The parameters describing the pre-
sliding regime are approximated by comparing the
pre-sliding behaviour in simulation with measure-
ments.
5 CLOSED-LOOP ROBOT
MODEL
The SPAC A R model of the manipulator mechanism,
the controller, the friction models and the robot drives
are assembled into a complete model of the closed-
loop robot system, Fig. 4.
The CS7B controller used in the St
¨
aubli RX90B
is an industrial PID controller based on the Adept
V+ operating- and motion control system. The con-
troller includes six SISO controllers, one for each
servo-motor. A trajectory generator computes the set-
points ¨q
(r)
, ˙q
(r)
and q
(r)
at a rate of 1 kHz. The
actual joint position q is compared with the set-point
q
(r)
and the error ² is fed into the P I-block of the
controller, which includes the proportional part and
the integrator part. The acceleration set-points
¨
q
(r)
and velocity set-points
˙
q
(r)
are used for accelera-
tion feed-forward and friction compensation, both in-
cluded in the F F -block. The friction compensation
includes both Coulomb and viscous friction. The ve-
locity feedback
˙
q is fed into the D-block, represent-
ing the differential part of the control scheme. The
block C represents the current loop, including the
power amplifier. Note that the position loop runs
at f
(1)
s
= 1 kHz and the velocity loop and current
loop run at f
(2)
s
= 4 kHz. The transfer functions
of the different blocks have been identified and im-
plemented in a SI MULINK block scheme of the robot
controller (Waiboer, 2004).
The current vector i is fed into the drive model
where the joint torques are computed. The LuGre
friction models compute the friction torques from
the joint velocities
˙
q. The net joint torque τ
(n)
in
(14) is the input for the non-linear manipulator model
(SPACAR). The output of the manipulator model con-
tains the joint positions, and velocities, denoted by q
REALISTIC DYNAMIC SIMULATION OF AN INDUSTRIAL ROBOT WITH JOINT FRICTION
51
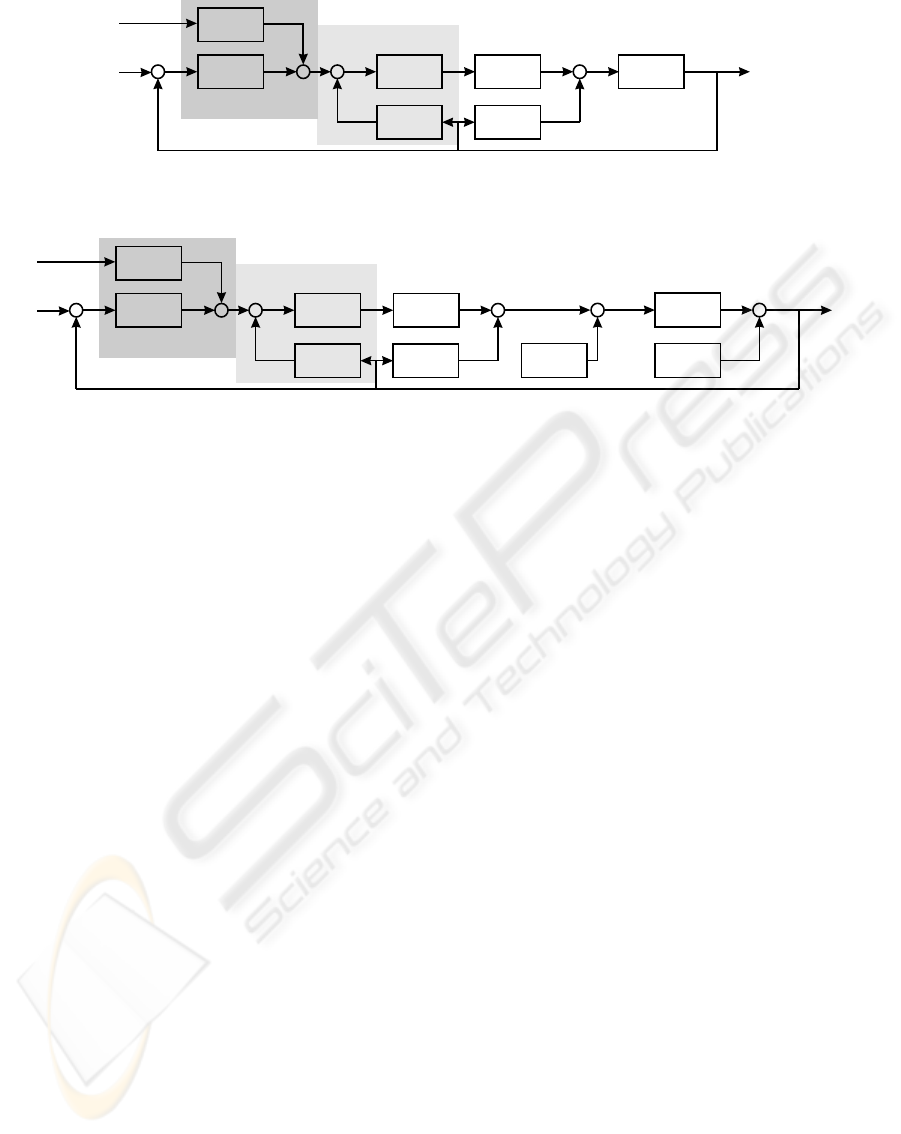
+
++
+
+
−
−
−
q
(r)
˙
q
(r)
¨
q
(r)
q
˙
q
˙
q
q
τ
(n)
τ
(f)
f
(1)
s
= 1kHz
f
(2)
s
= 4kHz
i
F F
P I
D
C
Drives
Friction
SPACAR
Figure 4: Assembly of the closed-loop robot model for a simulation with the non-linear finite element method (SPACAR
block).
+
++
+
+
+
++
−
−
−
−
q
(r)
˙
q
(r)
¨
q
(r)
q
˙
q
˙
q
q
F F
P I
D
C
i
Drives
Friction
τ
(n)
τ
(f)
f
s
= 1kHz
f
s
= 4kHz
y
0
read y
0
δy
δτ
(n)
τ
0
(n)
read τ
0
LT V
Figure 5: Perturbation scheme with the linearised equations of motion (LTV block).
and
˙
q, respectively.
6 PERTURBATION METHOD
In the presented closed-loop model, both the SPACAR
model and the friction model are continuous in time,
while the controller sections are discrete and running
at 1 kHz and 4 kHz, respectively. In SIMULINK this
implies that the SPACAR model is simulated at a time
step equal to 0.25 ms or even smaller if this is re-
quired by SIMUL I NK’s integrator. Due to the fact that
the position, computed within the SPACAR simulation
model, is obtained in an iterative way, the computa-
tion effort is quite elaborate. This results in long sim-
ulation times. In order to overcome this drawback,
the perturbation method (Jonker and Aarts, 2001) is
applied.
In the perturbation method, deviations from the
(nominal) desired motion (q
0
,
˙
q
0
,
¨
q
0
) due to joint
friction and errors of the control system are modelled
as first-order perturbations (δq, δ
˙
q, δ
¨
q) of the nomi-
nal motion, such that the actual variables are of the
form:
q = q
0
+ δq, (20)
˙
q =
˙
q
0
+ δ
˙
q, (21)
¨
q =
¨
q
0
+ δ
¨
q, (22)
where the prefix δ denotes a perturbation. Expanding
(1) and (3) in their Taylor series expansion and disre-
garding second and higher order terms results in the
linear approximations
δx = DF
0
·δq, (23)
δ
˙
x = DF
0
·δ
˙
q + (D
2
F
0
·
˙
q
0
)·δq. (24)
The subscript 0 refers to the nominal trajectory.
The nominal motion is computed first and is de-
scribed by the non-linear manipulator model. The
non-linear equations of motion (14) for the nominal
motion become
¯
M
(n)
0
¨
q
0
+ D
q
F
T
0
£
M
0
(D
2
F
0
·(
˙
q
0
))·(
˙
q
0
) − f
¤
+ DF
(e,c)
0
σ
(c)
0
= τ
(n)
0
,
(25)
where σ
(c)
0
= σ
(c,0)
+ k
s
e
(c)
0
. The right hand side
vector τ
(n)
0
represents the nominal net input torque
necessary to move the manipulator along the nomi-
nal (desired) trajectory. It is determined from an in-
verse dynamic analysis based on (25). Note that τ
(n)
0
is computed without the presence of friction. Obvi-
ously, the desired nominal motion (
¨
q
0
,
˙
q
0
, q
0
) equals
the reference motion (
¨
q
(r)
,
˙
q
(r)
, q
(r)
) of the closed
loop system.
Next the perturbed motion is described by a set
of linear time-varying equations of motion, which
are obtained by linearising the equations of motion
around a number of points on the nominal trajectory.
The resulting equations of motion for the perturba-
tions of the degrees of freedom δq are
¯
M
(n)
0
δ
¨
q + C
0
δ
˙
q +
¯
K
0
δq = δτ
(n)
, (26)
where
¯
M
(n)
0
is the reduced system mass matrix as in
(14), C
0
is the velocity sensitivity matrix. Matrix
¯
K
0
is a shorthand notation for the combined stiffness ma-
trices
¯
K
0
= K
0
+ N
0
+ G
0
, (27)
ICINCO 2004 - ROBOTICS AND AUTOMATION
52
where K
0
denotes the structural stiffness matrix, N
0
and G
0
are the dynamic stiffening matrix and the ge-
ometric stiffening matrix, respectively. The matrices
¯
M
(n)
0
, K
0
and G
0
are symmetric, but C
0
and N
0
need not to be symmetrical. Expressions for these
matrices are given in (Jonker and Aarts, 2001).
Fig. 5 shows the block scheme of the closed-loop
perturbation model. Note that the non-linear manip-
ulator model (SPACAR) is replaced by the LTV-block
which solves (26). Its input δτ
(n)
is computed ac-
cording to
δτ
(n)
= τ
(n)
− τ
(n)
0
, (28)
where τ
(n)
represents the vector of the net joint
torques as defined by (16). The perturbed output vec-
tor δy is added to the output vector y
0
of the nominal
model, yielding the actual output y. This output vec-
tor will be discussed below.
Within the SIMULINK framework the LTV block
represents a linear time-varying state space represen-
tation of a system
˙
x
ss
= A
ss
x
ss
+ B
ss
u
ss
y
ss
= C
ss
x
ss
(29)
where u
ss
, y
ss
and x
ss
are the input, output and state
vectors, respectively, and A
ss
, B
ss
and C
ss
are the
time-varying state space matrices. Equation (26) is
written in this representation by defining the state and
input vectors
x
ss
= [δ
˙
q, δq]
T
,
u
ss
= δτ
(n)
.
(30)
The state space matrices A
ss
and B
ss
are then com-
puted from the matrices in (26) using a straightfor-
ward procedure :
A
ss
=
"
0 I
−
¯
M
(n)
0
−1
¯
K
0
−
¯
M
(n)
0
−1
C
0
#
,
B
ss
=
"
0
¯
M
(n)
0
−1
#
.
(31)
The output matrix C
ss
depends on the output vector
y
ss
that is defined by the user. It may consist of (first
derivatives of) the degrees of freedom δq present in
x
ss
or (first derivatives of) nodal coordinates δx that
are computed from x
ss
using (23) and (24). E.g. the
coordinates δx in y
ss
are computed using
C
ss
= [
DF
0
0
] . (32)
For a practical implementation of the perturba-
tion method the total trajectory time T is divided
into intervals. The state space matrices and the vec-
tors τ
0
and y
0
are computed during a preprocess-
ing run at a number N of discrete time steps t = t
i
(i = 0, 1, 2, ..., N ) and stored in a file. During the
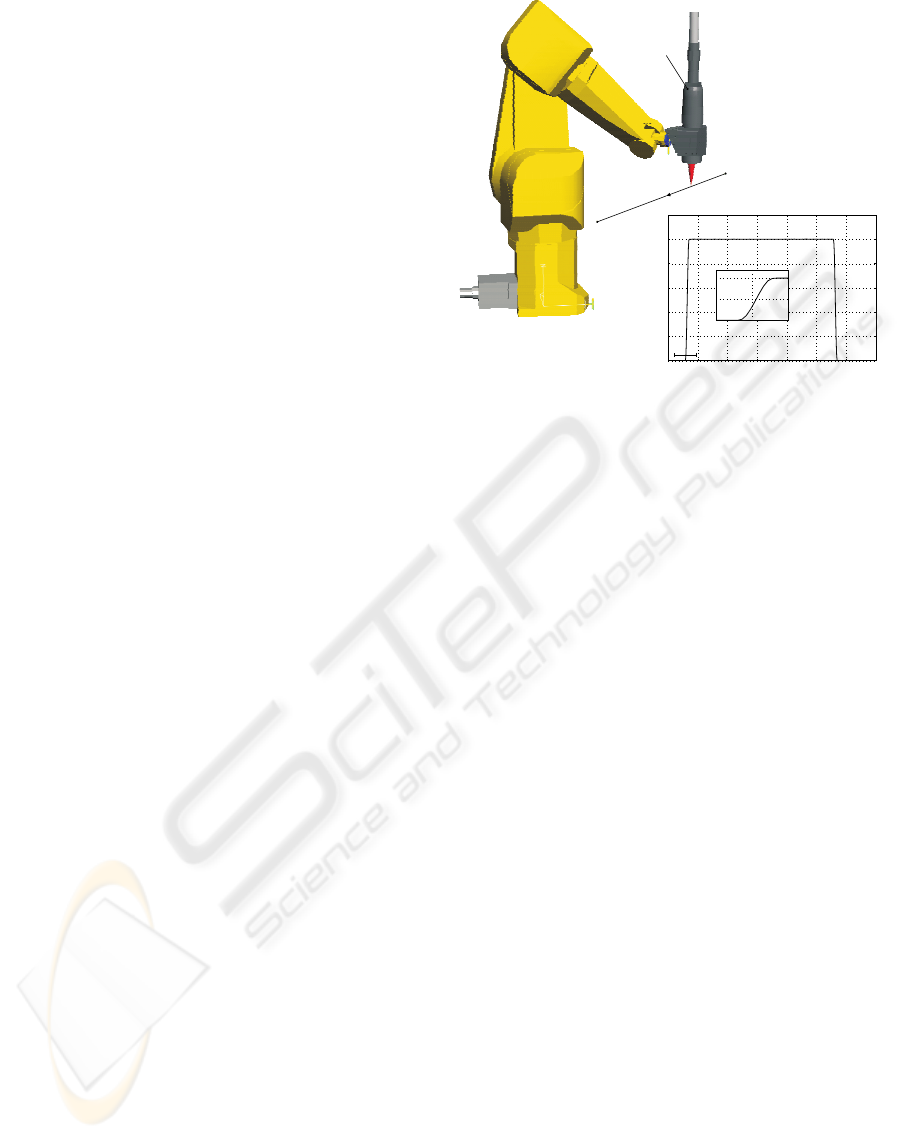
Welding
head
A
B
0
2 4
6 8 10
12 14
1
1.25 1.5
0
0
50
100
100
20
40
60
80
120
time [s]
Tip velocity [mm/s]
Figure 6: The simulated straight line path and the path ve-
locity.
simulation runs the matrices and vectors are then read
back from this file. Between two time steps the co-
efficients of the state space matrices are interpolated
linearly. Cubic interpolation is used for the vectors τ
0
and y
0
.
7 SIMULATION RESULTS
In Fig. 6 an experiment is defined in which a straight
line motion of the robot tip has to be performed in the
horizontal plane with a velocity profile as presented
in the insert. The welding head remains in the verti-
cal position as shown in Fig. 6. The joint set-points
are computed with the inverse kinematics module of
the SPACAR software. The joint velocities are shown
in Fig. 7. The figures show clearly the non-linear be-
haviour of the robot. Note the velocity reversal of
joints 2 and 3 nearly halfway the trajectory.
First, the trajectory will be simulated with the non-
linear model. The simulation has been performed in
SIMULIN K using the ode23tb integration scheme,
which is one of the stiff integrators in SIMULIN K.
The stiff integration scheme is needed due to the high
equivalent stiffness in the pre-sliding part of the fric-
tion model (18).
The path performance as predicted by the model
will be compared to measurements carried out on the
actual robot. In both the measurements and simula-
tions, the path position is based on joint axis positions
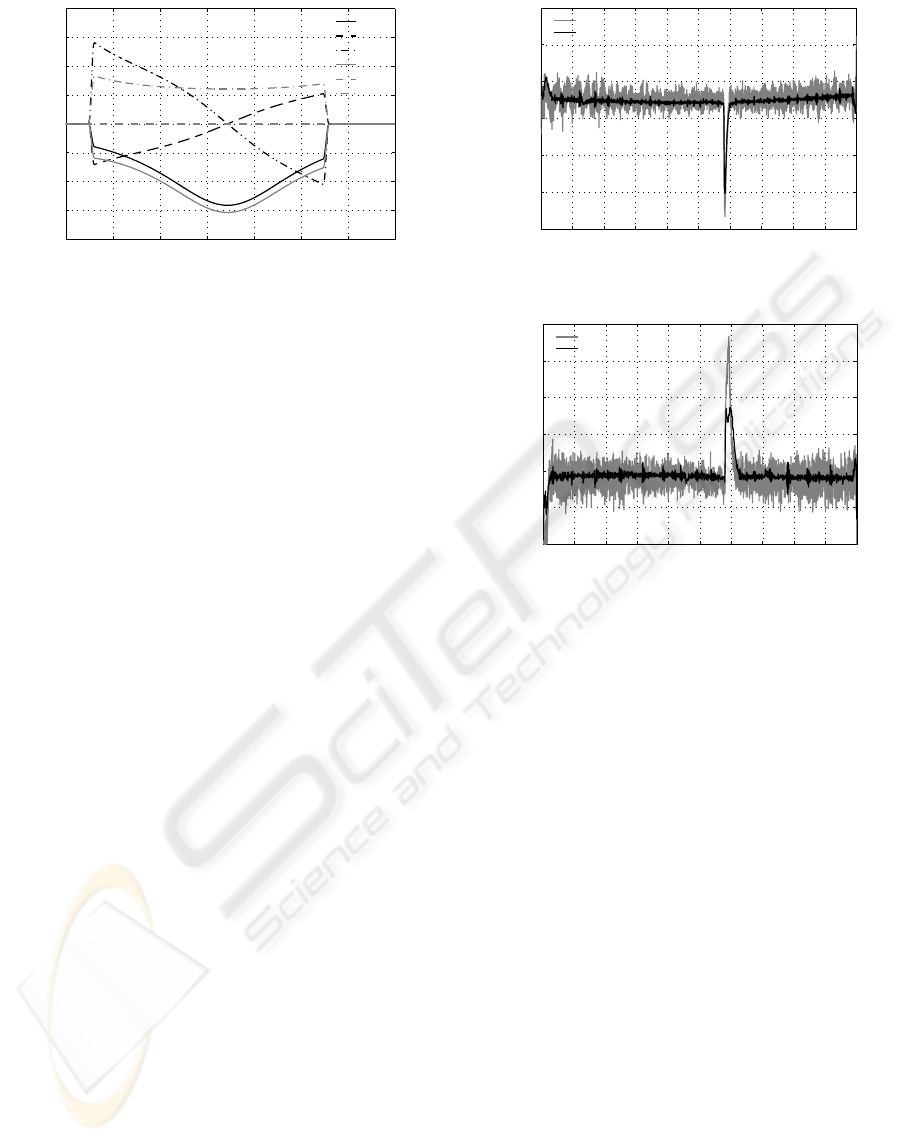
and the nominal kinematic model. In Fig. 8, the hor-
izontal and vertical path deviations are shown. The
results show that the agreement between the simu-
lated prediction and the measurement is within 20 µm
REALISTIC DYNAMIC SIMULATION OF AN INDUSTRIAL ROBOT WITH JOINT FRICTION
53
0
2
4
6 8 10
12
14
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
time [s]
V elocity [rad/s]
q
1
q
2
q
3
q
4
q
5
q
6
Figure 7: The joint velocity.
which is well within the range of accuracy required
for laser welding. At about 600 mm on the trajec-
tory, at the velocity reversal in joints 2 and 3, there is
a jump of the friction force, resulting in a relatively
large path error.
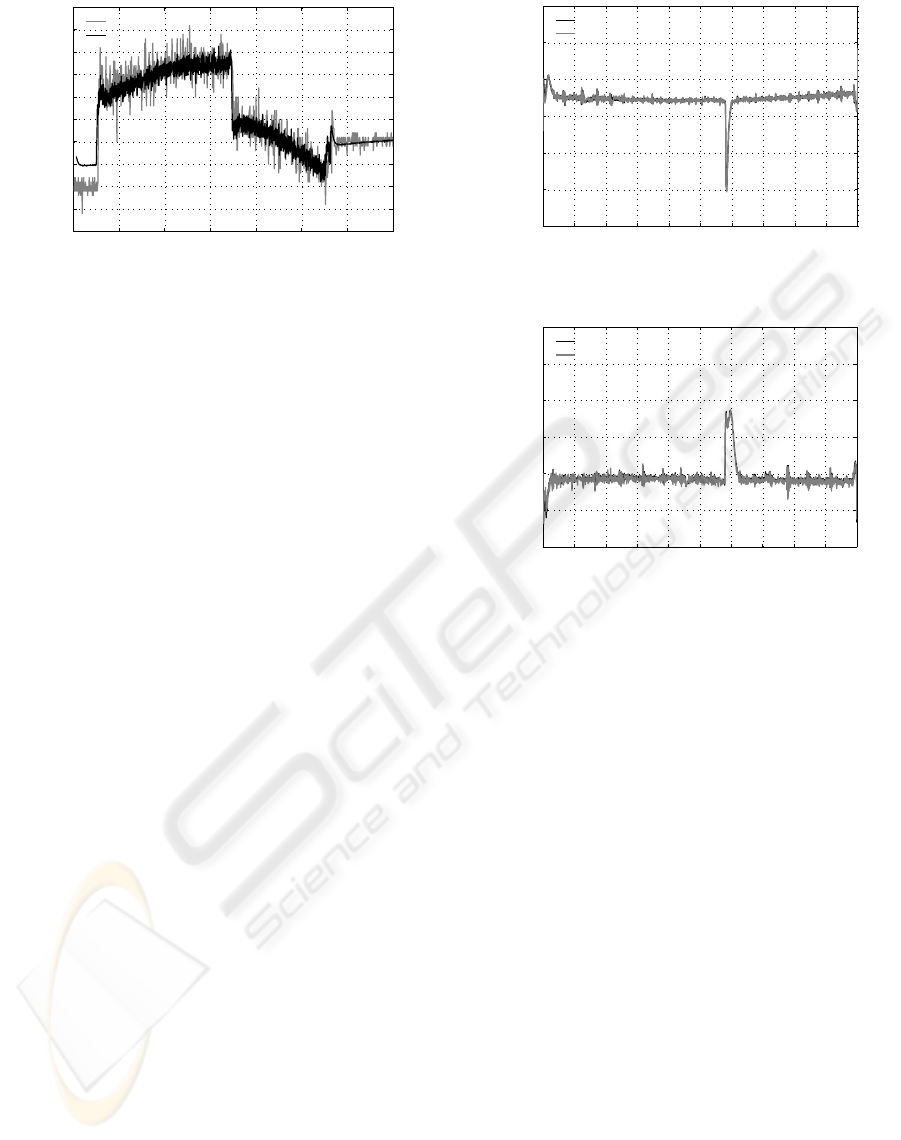
During the experiment the motor currents were
recorded. In Fig. 9 the measured motor currents of
joint 3 is compared with the simulated motor current
as an example. The simulation shows good agreement
with the measurements. It can be observed that the
motor currents are predicted quite accurately in the
sliding regime and near the velocity reversal. How-
ever, the model is unable to predict the stick-torques
with a high level of accuracy. This can be explained
by the fact that the stiction torque can be anywhere be-
tween τ
(s)
−
and τ
(s)
+
over a very small position range
of tenths of µrad, due to the high equivalent stiffness
c
(0)
in (18).
The required simulation time with the non-linear
simulation model was about 70 minutes on a 2.4 GHz
Pentium 4 PC, which indicates that it is computation-
ally quite intensive. This is caused by the small time
steps at which the manipulator configuration, see (1)
and (2), needs to be solved by an iterative method. To
overcome this drawback, the perturbation approach
will be used next.
For the perturbation method the number of points
along the trajectory N at which the system is lin-
earised is taken to be 400. The simulation results of
the perturbation method and the non-linear simulation
have been compared. Fig 10 shows the path accuracy
along the trajectory. There is no noticeable difference
between the results at this scale. The error stays well
below 10 µm and is mostly less than 2 µm. Also the
agreement between the simulated motor currents for
both the non-linear simulation and the perturbation
method is good, especially when the manipulator is in
motion. At rest, the torques in the stick or pre-sliding
regime shows some differences as before. A signifi-
cant reduction of simulation time by about a factor 10
0 200 400 600 800 1000
−0.08
−0.06
−0.04
−0.02
0
0.02
0.04
Measurement
Simulation
position [mm]
deviation [mm]
a. Horizontal deviation.
a. Horizontal deviation
0 200 400 600 800 1000
0.08
0.06
0.04
0.02
0
−0.02
−0.04
Measurement
Simulation
position [mm]
deviation [mm]
b. Vertical deviation.
b. Vertical deviation
Figure 8: Simulated and measured path deviation.
has been achieved.
8 CONCLUSIONS
In this paper a realistic dynamic simulation of a rigid
industrial robot has been presented. The following
components are essential for the closed-loop simula-
tion:
• A finite element-based robot model has been used
to model the mechanical part of the robot. Robot
identification has been applied to find the model pa-
rameters accurately.
• Furthermore, joint friction has been modelled using
the LuGre friction model.
• Finally, a controller model has been identified and
implemented.
The complete closed-loop model has been used for
the simulation of the motion of the robot tip along
a prescribed trajectory. The simulation results show
good agreement with the measurements. It was
found that a closed-loop simulation with the non-
linear robot model was very time consuming due
ICINCO 2004 - ROBOTICS AND AUTOMATION
54
0
2
4
6 8 10
12
14
−900
−800
−700
−600
−500
−400
−300
−200
−100
0
100
time [s]
Current [Counts]
Measurement
Simulation
Figure 9: Measured and simulated motor current for joint 3.
to the small time step imposed by the discrete con-
troller. Application of the perturbation method with
the linearised model yields a substantial reduction in
computer time without any loss of accuracy. The
non-linear finite element model and the perturbation
method can relatively easy be extended to account for
flexibilities in the robot.
ACKNOWLEDGMENT
This work was carried out under the project num-
ber MC8.00073 in the framework of the Strate-
gic Research programme of the Netherlands In-
stitute for Metals Research in the Netherlands
(http://www.nimr.nl/).
The authors acknowledge the work carried out on
the identification of the controller, inertia parameters
and friction parameters by W. Holterman, T. Harde-
man and A. Kool, respectively.
REFERENCES
Calafiore, G., Indri, M., and Bona, B. (2001). Robot
dynamic calibration: Optimal excitation trajectories
and experimental parameter estimation. Journal of
Robotic Systems, 18(2):55–68.
Haessig, D. and Friedland, B. (1991). On the modeling
and simulation of friction. Transactions of the ASME,
Journal of Dynamic Systems, Measurement and Con-
trol, 113(3):354–362.
Jonker, J. (1990). A finite element dynamic analysis of flex-
ible manipulators. International Journal of Robotics
Research, 9(4):59–74.
Jonker, J. and Aarts, R. (2001). A perturbation method for
dynamic analysis and simulation of flexible manipu-
lators. Multibody System Dynamics, 6(3):245–266.
Jonker, J. and Meijaard, J. (1990). Spacar-computer pro-
gram for dynamic analysis of flexible spatial mech-
0 200 400 600 800 1000
−0.08
−0.06
−0.04
−0.02
0
0.02
0.04
Non-linear
perturbation
position[mm]
deviation[mm]
a. Horizontal deviation.
a. Horizontal deviation
0
200 400 600 800 1000
0.08
0.06
0.04
0.02
0
−0.02
−0.04
Non-linear
perturbation
position[mm]
deviation[mm]
b. Vertical deviation.
b. Vertical deviation
Figure 10: Simulated path deviation (non-linear versus per-
turbation method).
anisms and manipulators. In Schiehlen, W., ed-
itor, Multibody systems handbook, pages 123–143.
Springer-Verlag, Berlin.
Swevers, J., Ganseman, C., Schutter, J. D., and Brussel,
H. V. (1996). Experimental robot identification using
optimised periodic trajectories. Mechanical Systems
and Signal Processing, 10(5):561–577.
Waiboer, R. R. (to be published, 2004). Dynamic robot sim-
ulation and identification – for Off-Line Programming
in robotised laser welding. PhD thesis, University of
Twente, The Netherlands.
Wit, C. d., Olsson, H.,
˚
Astr
¨
om, K., and Lischinsky, P.
(1995). A new model for control of systems with
friction. IEEE Transactions on Automatic Control,
40(3):419–425.
REALISTIC DYNAMIC SIMULATION OF AN INDUSTRIAL ROBOT WITH JOINT FRICTION
55
