DYNAMIC TOOLS TO CONTROL COMPLEX SYSTEMS
Mahfoud MABED
Laboratoire d’Ingenièrie des systèmes automatisés LISA FRE 2656 CNRS
Université d’Angers, 4 boulevard Lavoisier 49100 Angers, France
Keywords: Discrete event systems, Modeling, Petri nets, Scheduling
Abstract: The idea of complex sequencing is strongly related to scheduling and real time systems. It appears when a
resource has to be shared by more than one user or when a job must be handled by some concurrent entities.
The originality of our research is mainly to build a dynamic link between a scheduling solution and a
simulation approach based on Petri Nets (PN). This paper addresses with the modeling of an electroplating
line with max plus algebra theory and Petri Nets. As a schedule representing a sequence that contains a
series of jobs, we can obtain a corresponding polynomial by using Lagrange interpolation. Then, we can use
these polynomials to ensure a real time connection between a schedule procedure and a Petri nets
simulation. The use of this approach will lead us to deal with different disturbances. Indeed, for any
disturbance we should calculate a new schedule and a new polynomial will be found. This polynomial will
be assigned to Petri nets Model without modifying its structure.
1 INTRODUCTION
The scheduling approach is realized by using max
plus algebra theory. It is based on a model that we
have previously developed. We first look for a
mathematical model to find a cyclic schedule for
the hoist Scheduling Problem (HSP) (Bloch, 1999).
Therefore, concurrence appears for resource
utilization and only deterministic discrete event
systems can be described in the max algebra
(Gaubert, 1992). A relaxation is then proposed to
find a first solution. Then some heuristics (rules)
are introduced to respect resource constraints and
an admissible solution (schedule) is proposed.
The second approach is based on Petri nets
(PN) their practical use for discrete event systems
are well known in the literature. Nevertheless,
more powerful tools are necessary to deal with
some complex systems. The functions attached to
arcs in Colored Petri nets (CPN) sometimes seem
to be more difficult to understand. We propose
here to use Z/pZ Petri nets to model some complex
sequencing. A mathematical structure is defined to
represent the relation between the colors (Mabed,
2003).
This algebraic structure is an isomorphism
between a set of colors and a finite field Z/pZ.
2 PETRI NETS AND EVENT
GRAPH
A PN is a bipartite directed graph with two types
of nodes: the places and the transitions. These
nodes are joined by directed arcs. A transition X
i
is
enabled if and only if each of its input places
contains at least one token (assuming that the
weight of each arc is equal to 1).
It is also possible to assign a time to each place
or transition. In that case, the Petri net is called
respectively P-timed or T-timed Petri nets. Such a
time represents the time taken by the related
transition to fire.
In a P-Timed Petri Nets (P-TPN), a firing is
initiated by removing token from each of the input
places after a period of time equals to the time
assigned to the place. Then, one token appears in
each output place at the instant when the firing
terminates. The reader is referred to (Mabed, 2002)
for details.
An event graph is a Petri net such that each
place has exactly one input transition and one
output transition and such that every arc is 1-
weighted. In this way only synchronization
constraints (logical AND) can be represented,
whereas alternative choices (corresponding to
277
MABED M. (2004).
DYNAMIC TOOLS TO CONTROL COMPLEX SYSTEMS.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 277-284
DOI: 10.5220/0001144402770284
Copyright
c
 SciTePress

logical OR) cannot be represented. Figure (1) gives
an example of a P-timed event graph. Transition X
1
(resp X
2
) will be fired if there is a token in both
places P
1
and P
6
(resp P
3
and P
5
). In P
1
and P
3
,
token must spend a period of time equals
respectively to 1 and 2. This is the time assigned to
these tokens in these places before leaving.
3 MAX PLUS THEORY
The dioid IRmax = (IR∪{-∞},max,+) is an
algebraic structure with two operations, max as
addition (denoted by ⊕) and + as multiplication
(denoted by ⊗ or simply omitted). e= -∞ plays the
role of the null element for ⊕ (such that e⊕a=a)
and ε=0 plays the role of the unit element for ⊗
(such that a⊗ε=ε⊗a=a). We refer the reader to
(Cohen, 1989) (Spacek, 1998) to learn the main
properties of this structure.
The combinatorial properties of dioids (i.e.
associativity, commutativity of ⊕ and ⊗ and
distibutivity of ⊗ over ⊕), allow matrix
manipulations in a conventional way. It is no hard
to see that the following equations must hold for
the above example in figure 1.
X
i
(k) represents the date of the k
th
firing of
transition X
i
.
X
1
(k) ≥ U
1
(k) + 1 and X
1
(k) ≥ X
2
(k-1)
X
2
(k) ≥ U
2
(k-1) + 2 and X
2
(k) ≥ X
1
(k)
X
3
(k) ≥ X
1
(k) and X
3
(k) ≥ X
2
(k)
or
X
1
(k) ≥ max (X
2
(k-1),U
1
(k) + 1)
X
2
(k) ≥ max (X
1
(k), U
2
(k-1) + 2)
X
3
(k) ≥ max(X
1
(k), X
2
(k))
For instance X
2
(k) can be fired if the transitions
X
1
(k) and U
2
(k-1) have been fired and if the
minimum duration allowed to the places has been
respected.
X(k)≥
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
ε
εε
εεε
ee
e
X(k)⊕
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
εεε
εεε
εε e
X(k-1)
⊕
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
εε
εε
ε1
U(k) ⊕
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
εε
ε
εε
2
U(k-1)
We can easily write :
≥)k(X
v
0i=
⊕ A(i) X(k-i) ⊕
w
0j=
⊕ B(j) U(k-j)
We can solve this problem via rational methods
familiar in language theory (introducing “star”
operation A*=e ⊕ A ⊕ A
2
⊕ …⊕A
n
)
X(k) ≥
v
1i=
⊕ )ik(X)i(A − ⊕
w
0j=
⊕ )jk(U)j(B −
With
)i(A = (A(0))* A(i) and )j(B = (A(0))* B(j)
Figure 1:An event graph
ICINCO 2004 - ROBOTICS AND AUTOMATION
278

4 DESCRIPTION OF THE
PROBLEM
Production line fed with one or more hoists are
used in a large number of cyclic industrial
applications. The moving devices (hoists) transport
products from one station to another, according to
a sequence order. This problem is characterized by
the nature of the processing times, which are
variables of the model. Each of them has to take a
value in a given interval [t
i
, T
i
]. The result of a
schedule is firstly the sequence of the movements
and secondly the values of all processing times.
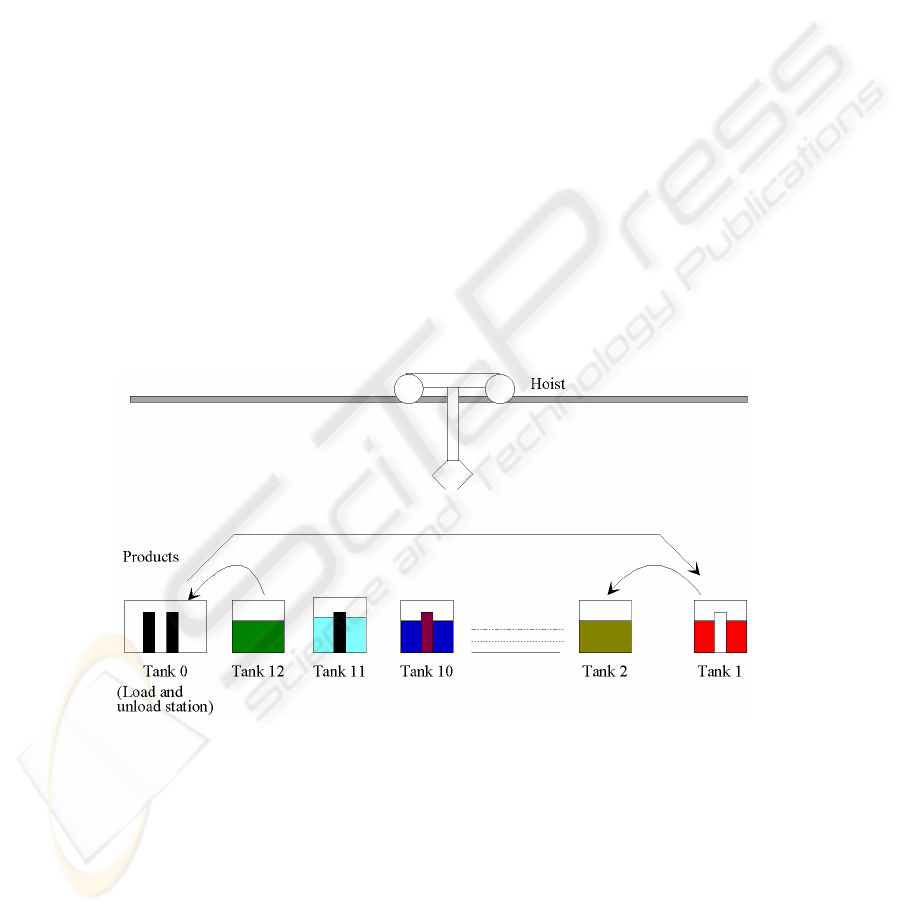
We consider a production line with 13 different
stations and one hoist. These stations are arranged
in a row and are fed with one hoist (Baptiste, 1993)
(Bloch, 1999).
The first station represented by tank (0), is a
shared station for both loading and unloading
purpose. A soak operation is performed in each
other station see figure 2. The hoist is programmed
to perform inter-process moves of the products.
Each one consists of four simple hoist operations:
− Raise a product from a process tank;
− Pause over the tank to allow drip-off;
− Transport the product to the next process tank
− Lower the product in that process tank
After performing an inter-process move, the
hoist travels to another process tank for the next
scheduled move. The following assumptions will
be respected throughout this presentation:
− The processing time in each tank is bounded
between a minimal and a maximum duration [t
i
, T
i
]
: i = 0 to 12;
− Each tank can receive only one product at the
same time;
− No buffer exists between tanks;
− We deal with mono-product case: each
product must respect the same sequence S=0,1,2,
3, …, 11, 12, 0.
5 SCHEDULING
Let us study the mono-products modeling case
(one hoist, tanks with unit capacity, same
processing for all the products, n products on the
line).Each product will be successively treated in
several tanks and then deposed into the load \
unloading station (tank(0)). There are two major
statuses: product transfer from a tank to another
one and processing. We will consider the notations
given below.
− X
i
(k) : the starting time to enable transition
Xi for the kth time;
− r
(i, i+1)
: the in charge hoist traveling time
from tank i to tank (i+1);
− t
i
, T
i
: minimum and maximum soak time
limits in tank i ;
− P
j
: Place number j
− Dv
(i, i+1)
: the empty hoist traveling time
from tank i to tank (i+1) ;
− U
i
(k) : command vector representing the
availability of the hoist;
Figure 2: An Electroplating line (1 hoist and 13 tanks)
DYNAMIC TOOLS TO CONTROL COMPLEX SYSTEMS
279

5.1 P-Timed Event Graph
Two labels are given with each place. The first one
(t) is the minimum time that a token entering the
place must spend. The second label (T) is the
maximum time that this token can spend in this
place. Each tank has its own given bounded time
intervals. If a token enters a place of Timed
Colored Petri Nets (TCPN), it must spend a
minimum time t
i
in this place and leave it at a
maximum time T
i
at the latest. Each time a tank is
emptied, it is immediately available for the next
product on the line. The last operation of each
product sequence is to unload it. We represent this
problem by an event graph figure 3.
The first tank (token(0)) filling the unloading
and loading tank, we will assume that there is no
event before this.
In figure 3 each time a transition is fired, it will
mean either a product is being transported from a
tank to another or that it is processed. We suppose
that the hoist is always available (otherwise
concurrence will appears for resource utilisation)
5.2 Mathematical Model
According to the previous example, we can
represent the event graph presented on figure 3 by
the following equations:
X
1
(k) ≥ X
3
(k-1) ⊕ (X
2
(k)⊗(-T
1
)) ⊕ V(k)
X
2
(k) ≥ U
1
(k) ⊕ (X
1
(k)⊗t
1
) ⊕ (X
3
(k)⊗(-r
1,2
))
X
3
(k) ≥ X
5
(k-1) ⊕ (X
4
(k)⊗(-T
2
)) ⊕ (X
2
(k)⊗r
1,2
)
X
4
(k) ≥ U
2
(k) ⊕ (X
3
(k)⊗t
2
) ⊕ (X
5
(k)⊗(-r
2,3
))
.
.
X
26
(k) ≥ U
13
(k) ⊕ (X
25
(k)⊗t
13
) ⊕ (X
27
(k)⊗(-r
13,1
))
X
27
(k) ≥ X
26
(k)⊗r
13,1
This system can be also written with matrix
notations:
and gives the vector :
)k(Vb)k(UB)1k(XA)k(*X
1
⊗⊕⊗⊕−⊗=
These vectors (k=1, 2,…,n) are represented by
a matrix. In each column, we can find the starting
time of transport or processing for each product k.
Nevertheless, this solution must be performed
according to the hoist constraints (ie. only one
hoist is available in the line). The hoist availability
constraint is the most restrictive one as the hoist
corresponds to a critical resource of the problem.
Each move of product k from the tank where its i
th
treatment occurs to the tank where its i+1
th
one
occurs, takes place in the following interval [X
i
(k),
X
i
(k)+ r
(i, i+1)
]. As all the movements are realized
by the same hoist, we must express that all these
intervals are disjoined. The objective here is to find
an admissible schedule from the solution proposed
by the (max, +) theory and then improve it to find
an optimal or a near optimal solution.
For all couples of transport operations of the
product k (resp k+1) from tank (i) (resp j) to tank
(i+1) (resp. j+1) either transport operation of k
preceeds transport operation of k+1 (case 1) or
Figure 3: Hoist scheduling P-Timed event graph
))k(UB())1k(XA())k(XA()k(X
10
⊗⊕−⊗⊕⊗≥
))k(Vb( ⊗⊕
ICINCO 2004 - ROBOTICS AND AUTOMATION
280

transport operation of k+1 preceeds transport
operation of k (case 2).
This kind of constraints are called disjunctions,
it corresponds to two mutually exclusive
constraints.
As we can see on the example detailed on
figure 4, we have two products k and (k+1) and
two operations request the same resource (hoist)
during a period of time:
− Move product k from tank 4 to tank 5, during
the interval [461,485]
− Move product k+1 from tank 2 to tank 3,
during the interval [443,472]
To deal with this conflict, we have to choose
between two cases as seen before. In figure 4 we
choose the case 2: transport operation of k+1
preceeds transport operation of k. It means that a
delay will affect the others tasks for this product.
The question is: how to choose how a conflict can
be treated? The transcription of our model into a
computable version is simply the translation of all
linear equations. When a solution is found, we
check that the hoist constraints are respected, if not
we try to resolve this conflict by an adapted
heuristic. We can notice that each conflict
corresponds to two alternatives and needs to make
a choice during the resolution.
In fact, when the resolution procedure reaches
a choice point it divides the search space into two
branches. Exploring all these solutions will take us
a long time. The situation has led us to develop a
new robust method governed by stochastic
methods. These methods (not developed in this
paper) serve as a meta-strategy to choose the best
way to deal with the management of the hoist
conflicts. The objective of this work is to explain
how to build a dynamic link between a scheduling
solution and a simulation approach based on PN.
Before modeling the electroplating line we
should present how we can translate this schedule
to a polynomial. As a schedule represents a
sequence that contains a series of jobs, we can
obtain a corresponding polynomial by using
Lagrange interpolation. Then, this polynomial will
be used to valuate PN arcs.
5.3 Example
Let us consider a simple sequence S representing a
schedule:
S =(S
0
,S
1
,…,S
(p-1)
)
We can obtain the corresponding polynomial
P(X) by defining a finite ring structure with p
distinct elements {0, 1, 2, …, p-1} isomorphic with
Z/pZ (p: prime). On this set, we define a
polynomial function P(X) as an automorphism of
Z/pZ.
∑
−
=
=
1p
0i
P(X)
a
i
X
i
Fi
g
ure 4: How to deal with conflicts
(
case 2
)
DYNAMIC TOOLS TO CONTROL COMPLEX SYSTEMS
281

1p1p1p1p
1)2p()1p(0
1p)2p)(1p()1p)(1p(0
1)2p()1p(0
0001
)4p()4p(
)3p()3p(
)2p()2p(
−−−−
−−
−−−−−
−−
−−
−−
−−
K
KKKKK
K
K
K
K
6666666
1234560
6355360
1161660
6533560
1452360
0000001
A polynomial in Z/pZ[X] is completely given
by its coefficients A
0
to A
(p-1)
. We already prove
that a matrix [L
p
] exists there, making the
correspondence between the p elements of S.
t
[A
0
, A
1
, …, A
(p-1)
]=[L
p
].
t
[S
0
S
1
… S
(p-1)
]
[
p
k
L
(X)]= [1 X X
2
… X
(p-1)
]. [L
p
]. [I
k
]
Where I
k
is a column matrix whose elements: equal
1 in k
th
row and = 0 elsewhere.
[
p
k
L
(X)] is a (p-1) degree polynomial verifying the
conditions:
[
p
k
L (k)]=1 and [
p
k
L (X)]= 0, ∀ X≠k
This polynomial is the interpolation Lagrange
polynomial, which can be written, if considering
the first theorem of Fermat :
[
p
k
L (X)]= 1+(p-1)(X+p-k)
(p-1)
When we develop (X+p-k)
(p-1)
by Newton’s
binomial in Z/pZ, we obtain [L
p
] matrix:
[L
p
]=
Let us apply this method to the sequencing
vector S=(0,6,1,4,2,5,3), for p=7 the matrix [L
7
] is
:
[L
7
]=
P(X)= [1 X X
2
… X
6
].[L
7
].[F]
with [F]=
t
[P(0) P(1) P(2) P(3) P(4) P(5) P(6)] thus
equal to
t
[6 4 5 0 2 3 1].
We obtain P(X) =6+6.X+6.X
2
+X
4
+6.X
5
and easily verify that P(0)=6, P(6)=1, P(1)=4,
P(4)=2, P(2)=5, P(5)=3, P(3)=0;
As said before if the length of the sequence
does not correspond to a prime number (n<p), we
go back to the previous case and consider (p-m)
fictitious tasks that will not be used.
6 MODELING :Z/PZ TPN
REACTIVE MODEL
A complex system needs to be dynamically
controlled. Even, if the polynomials introduced in
this presentation show a clear evolution of the
standard functions used in traditional TCPN, a
characteristic does remain specific to all these
polynomials. It consists of the definition of the
color set. In Z/pZ TPN, there is only a global color
set and all the polynomials take its values in it.
This is why a circumstantial readjustment is
always possible (Mabed, 2003).The first tank
(token (0)) filling the unloading and loading tank,
we will assume that there is no event before this. In
this Petri Nets, tokens represent tanks. Each time a
transition is fired, it means either a product is being
transported from a tank to another, or that it is
processed.
We are interested here in modeling an
electroplating line with Z/pZ Timed Petri Nets
(TPN). It illustrates that these nets can be easily
applied to various industrial problems. Modifying
a sequence leads to change the Z/pZ TPN
parameters (i.e. polynomial) while the net structure
remains the same.
NB: For a simple use of Petri Nets parameters we
replace T
i
(the maximum duration in tank i) by δ
i
,
T
i
will represent the transition i.
Petri nets have been traditionally employed in
simulating approaches based on discrete event
systems. Here we create a dynamic link between
two fields:
− Scheduling approach: based on several
stochastic or deterministic methods.
− Simulation approach based on Petri nets.
We present in figure 5 a global model for the
HSP problem. This model was built in two
sections: first, we create a PN model and secondly
we assign polynomials to this PN. When we
elaborate this model, several difficulties were
encountered due to the two associated stations
(loading, unloading) represented by tank (0). The
first operation is to load the product, which is
represented by a processing (color (0) in place P
3
).
After a minimal duration of soak the product can
leave this tank (represented by color (0)) to another
one (represented by the successor of (0)+1=(1))
according to the set definition
E={0,1,2,3,4,5,…,10,11,12}. Each product will be
successively treated in several tanks and then
deposed into the load \ unloading station (tank(0)).
There are two major statuses:
ICINCO 2004 - ROBOTICS AND AUTOMATION
282

− Product transfer from a tank to another one:
The sequence representing the schedule has been
realized by the calculus of a polynomial SC. This
polynomial characterizes the results of max plus
approach.
− Processing
These operations will continue until we use the
color (12), its successor will be (0) and the
transition T
8
will be fired to unload the product.
Each evolution or disturbance lead this set
unchanged. Only the parameters are to be changed.
The model presented below allows a dynamic
management.
7 CONCLUSION
The originality of this study is mainly to apply
both: max plus algebra theory and Z/pZ TPN for
modeling and evaluating an industrial problem. We
have seen in this paper that a model can be
dynamically controlled by combining existing
tools.
We first use max plus algebra theory to find a
schedule for an industrial application known as a
hoist scheduling problem. Using the analogy
between timed event graphs and conventional
linear systems lead us to propose a schedule
approach. The critical point in this work is to
improve the results in order to find an optimal
solution. The use of stochastic methods to explore
more solutions can be the best way to reach this
objective.
After this, we present a model by using Z/pZ
Timed Petri Nets in order to control this system. A
structure of field Z/pZ is proposed to allow the
processing of colors succession with mathematics.
This mathematical structure allows an easy
modeling of sequences by polynomials and
symbolic calculation.
Furthermore, mathematical support may enable
us to consider various problem of optimization,
particularly those dealing with the resolution of
scheduling problems, one of our points of interest.
Figure 5: Z/pZ TPN Reactive Model
DYNAMIC TOOLS TO CONTROL COMPLEX SYSTEMS
283

We also note that this approach offers many
advantages to deal with complex models.
Developing these polynomials to evaluate models
facilitates modeling any kind of systems. This new
tool can be used as basis for further studies on
scheduling.
REFERENCES
Bacelli, F., Cohen, G., Olsder, G.J., Quadrat, J.P. (1992).
Synchronisation and linearity : An algebra for
discrete Event Systems. John Wiley and Sons, New
York.
Baptiste, P., Legeard, B. (1993). Optimisation with
constraint logic programming : The Hoist scheduling
problem solved with various solvers. 8th
International Conference on Applications of
Artificial Intelligence in Engineering, AIENG/93,
Toulouse, France.
Bloch, C. (1999). Contribution à l'ordonnancement
dynamiques de lignes de traitement de surface.
Thèse de Doctorat, Laboratoire d'Automatique de
Besançon (UMR CNRS 6596), Université de
Franche-Comté.
Borevitch, Z-I., Chafarevitch, I-R (1967). Théorie des
Nombres, (Gauthier-Villars), Paris.
Bourcerie, M., Morel, J-Y. (1997). Algebraically
structured coloured Petri nets to model sequential
processes. IEEE Transactions on Systems, Man and
Cybernetics, Part B : Cybernetics, Vol. 27, n°4.
Cohen, G., Dubois, Quadrat, J.P., Viot, M. (1985). A
linear system theoric view of discret-event processes
and its use for performance evaluation in
manufacturing. IEEE Trans. Automatic Control, 30 :
210-220.
Cohen, G., Moller, P.,Quadrat, J.P.,Viot, M.,: Algebraic
tools for the performance evaluation of discrete
event systems. Proceeding of the IEEE, Vol.77, pp.
39-58, 1989.
Gaubert, S. (1992). Théorie des systèmes linéaires dans
les dioïdes. Thèse de doctorat, Ecole des mines de
Paris.
Mabed, M. (2002).Thèse de doctorat intitulée,
Utilisation de l’Algèbre (Max, +) et des réseaux de
Petri Z/pZ dans l’étude d’un processus industriel.
Université d’Angers, octobre 2002.
Mabed, M., Bourcerie, M., Bousseau, F. (2001). Z/pZ
Petri nets model with application to an electroplating
line. IEEE International Conference on Systems,
Man and Cybernetics october 7-10, 2001, Tucson,
Arizona, USA.
Mabed, M., Bourcerie, M. (2003). Real-time model for
processing both scheduling and petri nets
approaches. European Simulation and Modelling
conference ESMC’03, October 27-29, 2003, Italy.
Marteau, S., Bourcerie, M. (1995).Complex sequencing
by methods of interpolation in Z/pZ colored Petri
nets, 4th International Conference on Emerging
Technologies and Factory Automation INRIA /
IEEE ETFA'95, p 573-581, France.
Marteau, S., Bourcerie, M. (1996). Dynamic evolution of
Z/pZ colored Petri nets models. In : Computational
Engineering in Systems Applications, Symposium
on Discrete Events and Manufacturing Systems
(IEEE-SMC CESA'96), p. 48-52, Lille, France.
Proth, J-M. Xie, X.(1994) Les réseaux de Petri pour la
conception et la gestion de systèmes de production,
Masson, Paris.
Spacek, P. (1998). Modélisation, analyse et commande
des systèmes à événements discrets par l'algèbre des
dioïdes, Application aux lignes de galvanoplastie.
Thèse de troisième cycle, Université de Franche
Comté
ICINCO 2004 - ROBOTICS AND AUTOMATION
284