
AN LMI-BASED GENETIC ALGORITHM FOR GUARANTEED
COST CONTROL
G.A.Papakostas, O.I. Kosmidou and I.E. Antonakis
Democritus University of Thrace, Department of Electrical and Computer Engineering, 67100 Xanthi, Greece
Keywords: Genetic Algorithms, Linear Matrix Inequalities, Robust Control, Guaranteed Cost Control
Abstract: In this paper a new approach for the Guaranteed Cost Control Problem (GCCP) is presented, using two
efficient tools, Linear Matrix Inequalities (LMIs) and Genetic Algorithms (GAs). A linear system with
parametric uncertainty is considered for which a control law is to be found, minimizing a performance
index. In a previous paper, an efficient method has been presented by using an LMI optimisation technique.
A combined use of LMIs and GAs is proposed in the present approach that allows further improvement of
the design procedure.
1 INTRODUCTION
The guaranteed cost control problem (GCCP) has
drawn considerable attention in the last few years
(Kosmidou, 1991), since the inclusion of
uncertainties in the system model, with the
appearance of robust control theory, is a standard
practice. Most of the approaches to this problem
make use of linear optimization techniques to find
best solutions that satisfy some constraints of a
specified problem. For convex problems, LMI
techniques are now very efficient (Fischman, 1996).
However, searching methods have the major
drawback due to the fact that they may converge to a
local minimum or maximum.
Genetic Algorithms (GAs) come to negotiate this
drawback, providing an alternative stochastic
searching process, in which the natural evolutionary
theory is adapted. Successive application of GAs in
control theory has led to very promising results
(Kundu, 1996).
In this paper, a new genetic algorithm is
presented, which makes use of the LMI tool to
compute the fitness value, of its candidate solution
of the current population.
The paper is organized as follows: In Section 2
the guaranteed cost control problem is formulated. A
general presentation of Genetic Algorithms and the
basic operators they used is given in Section 3. The
main idea of the proposed technique is described in
details in Section 4, while an experimental
verification of this method is performed through a
numerical example, in Section 5. Finally, Section 6
presents conclusions and perspectives.
2 PROBLEM FORMULATION
Consider the linear uncertain system in state-space
representation
() ()( )() ()()
tutBBtxtAAtx ∆++∆+=
0
.
()
(1)
where x(t)∈R
n
is the state vector, u(t)∈R
m
is the
control vector, A
0
and B
0
are the state and control
matrices, respectively, having appropriate
dimensions.
The system uncertainties are described by
() () ()
() () ()
1,
1,
2
1
2
1
≤=∆
≤=∆
∑
∑
=
=
tbBtbtB
taAtatA
i
q
i
ii
i
p
i
ii
(2)
where the scalars a
i
(t), b
i
(t) are uncertain parameters,
possibly time-varying, belonging to specified ranges,
and A
i
, B
i
are given constant matrices determining
the uncertainty structure. Without loss of generality,
one can always assume that A
i
, B
i
have unity rank
327
A. Papakostas G., I. Kosmidou O. and E. Antonakis I. (2004).
AN LMI-BASED GENETIC ALGORITHM FOR GUARANTEED COST CONTROL.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 327-333
DOI: 10.5220/0001145303270333
Copyright
c
SciTePress

and thus they may be decomposed in form of
products of vectors of appropriate dimensions, as
follows:
T
iii
T
iii
gfBedA == ;
(3)
This is called the rank-1 decomposition. By
using these vectors, define the matrices
[
]
[
]
[] [ ]
() (
qp
T
q
T
p
qp
ttdiagTssdiagS
ggGeeE
ffFddD
...:...:
...:...:
...:...:
11
11
11
==
==
==
)
(4)
where s
i
, i=1,…,p and t
i
, i=1,…,q are positive
scalars. Since decomposition (3) is not unique, these
scalars may be chosen to determine a suitable rank-1
decomposition in order to satisfy different design
requirements. In other words the elements S, T will
be treated as free parameters, in the design
procedure.
Consider also the quadratic performance index of
the form:
()( ) () () () ()
∫
∞
+=
0
000
][, dttuRtutxQtxtuxJ
TT
(5)
with Q
0
>0, R
0
>0 .
As shown in (Kosmidou, 1996, Fischman, 1996)
the guaranteed cost control law of the form
() ()
tPxBRtu
T1* −
−=
δ
(6)
ensures an upper bound of the quadratic
performance index (5) for all parameter variations
consistent with (2), called guaranteed cost,
()
(
)
() ()
00
**
PxxJtuJ
T
=≤
(7)
The nxn matrix P is the positive definite solution
of the modified Riccati equation associated with the
GCC problem,
0]
)
([
1
111
1
=++−−
−−+
−
−−−
−
QESEPDSDFTF
BGRTGBR
BBRPPAPA
TTT
TT
TT
δ
δ
has been proposed in
(Fis
thod, by involving genetic algorithms,
for the searching of the free parameters (S, T, δ) of
the system.
, depending on the specific
app
, there are some specific
pro
he sequel, terminology in the field of genetic
me ods for optimization and searching purposes is
giv
is a solution of a problem satisfying
the
cha
ystems. The fitter
(8)
The scalar δ and the scaling matrices S, T are
chosen by the designer.
Since the GCC problem is often related with
conservatism, i.e. the resulting upper bounds are too
large with respect to the minimal J obtained from the
LQR optimal design for the system without
uncertainty, it is desirable to make J
*
as small as
possible. This leads to an auxiliary optimization
problem, which is often analytically not tractable.
An efficient solution
chman, 1996) by solving an LMI objective
minimization problem.
That approach is being improved using the
proposed me
3 GENETIC ALGORITHMS
Genetic Algorithms (GAs) have played a major role
in many applications of the Engineering Science. As
mentioned above, GAs constitute a powerful tool to
optimization tasks. In other words, a simple GA is a
stochastic method that performs searching in wide
search spaces and depends on some probability
values. For these reasons as well as its parallel
nature, it has the ability to converge to the global
minimum or maximum
lication, and to skip possible local minima or
maxima, respectively.
The main idea in which GAs are based, was first
inspired by J. Holland (Holland, 2001). He tried to
find a method to imitate the evolutionary process
that characterizes the evolution of living organisms.
This theory is based on the mechanism qualified by
the survival of the fittest individuals over a
population. In fact
cedures taking place until the predominance of
the fittest individual.
In t
th
en:
Individual
constraints and demands of the system in which
it belongs.
Population is a set of candidate solutions of the
problem, which contains the final solution.
Fitness is a real number value, which
racterizes any solution and indicates how proper
is this solution for the problem under consideration.
Selection is an operator applied to the current
population, in a manner similar to the one of natural
selection found in biological s
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
328
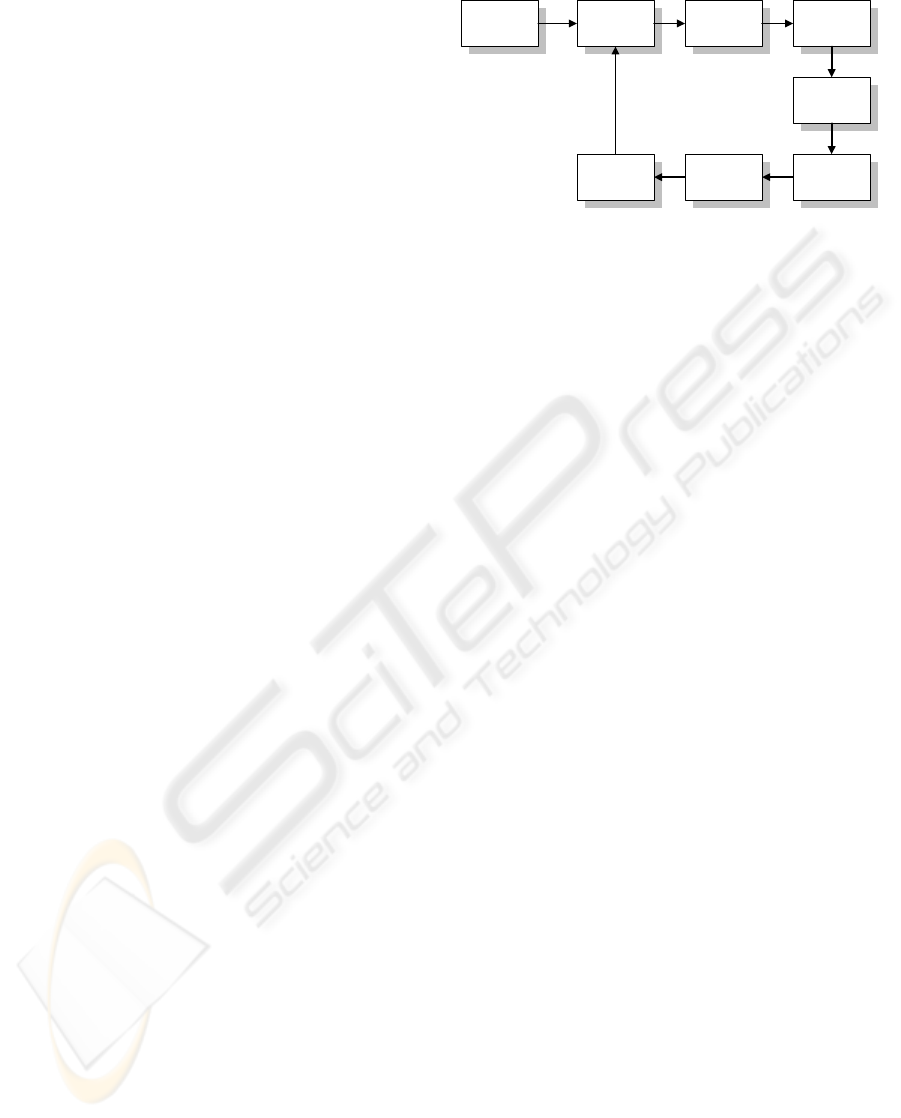
indi
d and new
can
sin
ext population, and also an
acc
. According to this
pro
ue until a predefined
num
imple Genetic Algorithm, which uses some
of the operations discussed above, is presented in
Fig.1.
viduals are promoted to the next population and
poorer individuals are discarded.
Crossover is the second operator that follows the
previous one. This operator allows solutions to
exchange information, in such a way that the living
organisms use in order to reproduce themselves.
More specifically, two solutions are selected to
exchange their sub-strings from a single point and
after (single point crossover), according to a
predefined probability P
c
. The resulting offsprings
carry some information from their parents. In this
way new individuals are produce
Initial
population
Decode
the
population
Find
Fitness
Selection
Crossover
MutationReplace
New
population
didate solutions are tested in order to find the one
that satisfies the appropriate objective.
Mutation is the third operator that can be applied
to an individual. According to this operation each
Figure 1: Block diagram of a simple GA
In the next section, an LMI-based genetic
algorithm is proposed and applied to the guaranteed
cost control problem described in Section 2.
gle bit of an individual binary string, can be
flipped with respect to a predefined probability P
m
.
There is a different procedure that can be
considered for a single iteration of a genetic
algorithm, called Elitism. During this operation the
probability of discarding the fittest individual is
minimized, since at each generated population, the
fittest individual is checked whether it has a lower
fitness than the elite member of the previous
generation. If so, a randomly selected individual is
replaced by the old elite member. Thus, it is
guaranteed that the fittest individual will be
promoted to the n
4 LMI-GENETIC METHOD
As previously mentioned, a first attempt of using
LMI optimizations in Guaranteed Cost Control
(Fischman, 1996) appeared very promising. Besides,
genetic algorithms seem to be very efficient in
solving various optimization problems in which the
searching space is complex.
In the proposed method, a combination of two
optimization tools is used. More precisely, the
genetic algorithm is used to find a suitable variable
set (S, T, δ), while the LMI optimization, used in
(Fischman, 1996) is applied to find an optimum
matrix P that satisfies some prespecified constraints.
By using the obtained matrix P, a fitness value is
assigned to the corresponding candidates and
process goes on.
eleration of the overall speed of the algorithm is
derived in this way.
In the present algorithm, an elitism based
reinsertion method is used
cess, a predefined number of individuals (the
least suitable) are replaced.
Since these operators have been applied to the
current population, a new population will be formed
and the generational counter will be increased by
one. This process will contin
This method can be viewed as a simple genetic
algorithm that uses the LMI tool to find the fitness
of the resulting candidate individuals of the problem,
under consideration.
ber of generations is attained or some form of
convergence criterion is met.
A s
To be more specific, consider the modified
genetic algorithm depicted in Fig. 2. This algorithm
is similar to the simple genetic algorithm of Fig.1,
with the difference that an LMI optimization
mechanism is used, to compute the objective value
of the current candidate solutions.
AN LMI-BASED GENETIC ALGORITHM FOR GUARANTEED COST CONTROL
329
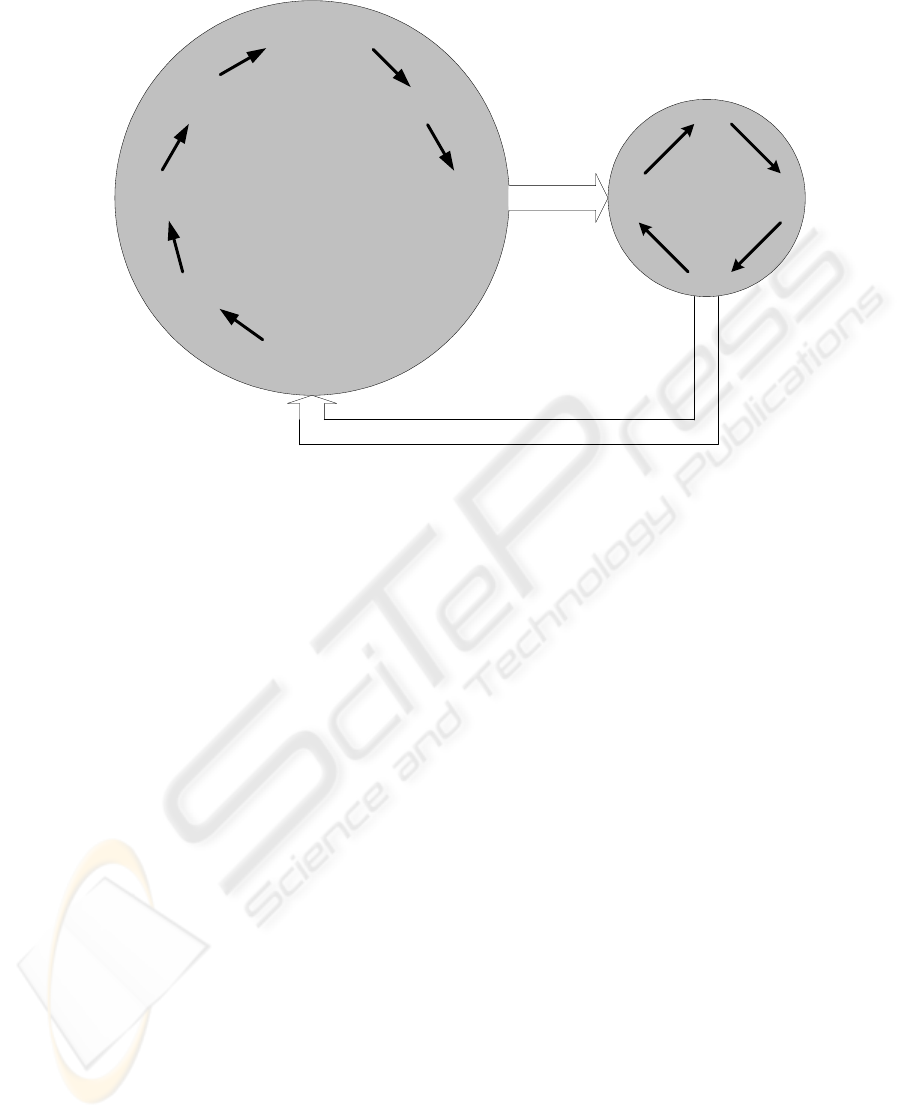
J
Genetic
Algorithm
LMI
Optimization
S, T, δ
Fitness
Assignment
Crossover
Selection
Mutation
Reinsertion
Population
Figure 2: The proposed LMI-based Genetic Algorithm
The LMI optimization procedure described in
Fig.2, consists of the following Theorem which is a
modified version of Theorem 3 in (Fischman, 1996)
and stated as,
Theorem
The minimization of the value of the guaranteed
cost (5) for the uncertain system (1) is ensured by a
control law of the form (6), if the optimization
problem described by equation (9) has a non empty
set of feasible solutions (M, W) with M, W being
symmetric positive definite matrices, and P = W
-1
.
The difference of the above Theorem from
Theorem 3 of (Fischman, 1996) is that the matrices
S, T and the scalar δ, are not variables of the LMI
optimization process, but constant values that come
from the genetic algorithm.
In other words, the genetic procedure manages to
find candidate sets of the (S, T, δ) variables, and
passes these sets into the LMI optimization for
finding optimal value of the matrix P.
The resulted matrix P is used in equation (7) to
derive the corresponding guaranteed cost, with a
known initial condition x
0
.
Before the beginning of the proposed algorithm,
one has to take some decisions about the parameters
that must be defined, in order to initialize the
procedure. Some of these parameters are (Coley,
2001)
• Type of individual representation (real,
binary, etc.)
• Population size (typical values are 20-
100)
• Length of individuals (L, depends on
the range of the parameters)
• Crossover probability (P
c
: typical
values are 0.4-0.9)
• Mutation probability (P
m
=1/L, 0.01)
• The selection operator
• Number of Generations
The proposed algorithm can be summarized in the
following steps:
Algorithm
Step 1: Generation of the initial population,
consisting of 100 individuals. Each
individual contains, three variables (S,
T, δ), in binary representation, of
length 20 each one.
Step 2: The candidate sets of the variables (S,
T, δ) are appeared as solutions of the
problem. Each one of this set, is
passed as constant matrices into
equation (9), and the LMI procedure is
started.
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
330

Step 3: The resulted matrix P is used to
compute the guaranteed cost that
corresponds to the set of (S, T, δ), by
using (7).
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−−
−−
=
00000.100
3229.17070.02855.01002.0
0208.40024.00100.10482.0
4555.00188.00271.00366.0
0
A
,
()
()
()
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
>
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−+−−
>
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−−
0
00
00
00
0
1
0
1
0
1
0
1
0
,
min
QW
TBGR
SEW
WGBRWEFTFDSDBBRAWWA
ii
WI
IM
i
MTr
T
TTTTTT
WM
δ
δδ
(9)
Step 4: The computed cost J, consists the
objective value of the respective set
(S, T, δ), and is used for the fitness
assignment operator of the genetic
algorithm.
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
00
9900.45200.5
5922.70447.3
1761.04422.0
0
B
Step 5: The algorithm continues, by applying
the genetic operators, presented in
Fig.2, with the appropriate settings.
with the uncertainty matrices:
Step 6: A new population is obtained and the
algorithm goes to Step 2 until a fixed
number of generations is achieved.
()
() ()
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=∆
0000
2031.102192.00
0000
0000
11
tata
tA
When the above algorithm has been terminated,
the individual with the higher fitness value is the
solution of the respective problem. Thus the
variables that consist the fitter individual, is the
optimum set of problem variables (S, T, δ), which
obtains a minimum guaranteed cost control J*.
()
()
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=∆
00
00
00673.1
00
1
tb
tB
The above algorithm is now illustrated by means
of a numerical example.
Let the uncertainty decomposition matrices be as
follows:
5 NUMERICAL EXAMPLE
[]
,101822.00,
0
2031.1
0
0
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
= ED
A common problem (Kosmidou, 1996, Fischman,
1996) is considered in this section in order to
investigate the performance that can be achieved by
using the proposed method.
This problem represents a 4
th
order model of a
helicopter in a vertical plane for an airspeed range of
60 knots to 170 knots. For this range of operating
conditions significant changes occur in elements a
32
,
a
34
and b
21
of the system matrices, where the
nominal matrices are the following:
[]
05.0,
0
0
1346.2
0
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
= GF
while the R
0
= I
2
and Q
0
= I
4
.
AN LMI-BASED GENETIC ALGORITHM FOR GUARANTEED COST CONTROL
331
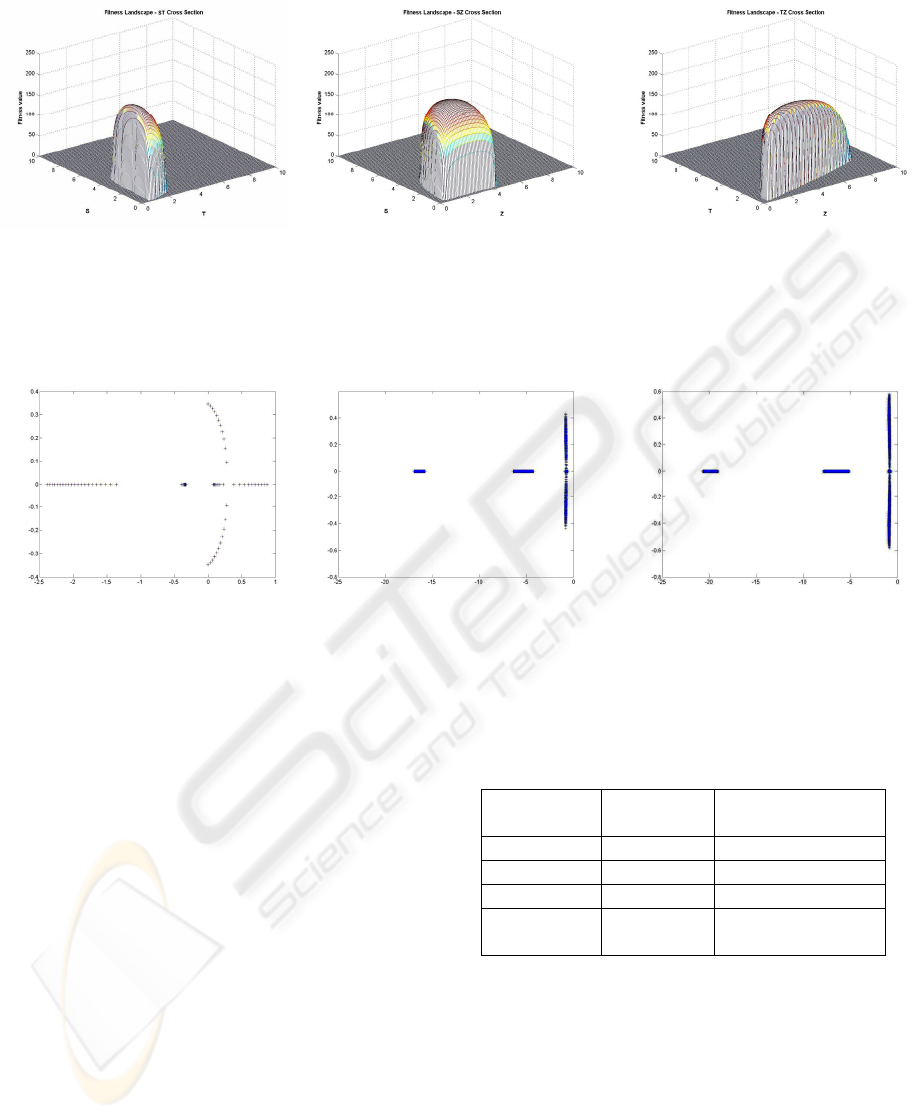
(a)
(b) (c)
Figure 3: Fitness landscape in three cross sections, of the proposed genetic algorithm, (a) ST, (b) SZ and (c) TZ cross sections
(a)
(b)
(c)
Figure 4: The complex plane with the poles of (a) open system, (b) closed loop system with the control law of (
Fischman,
1996),
and (c) closed loop system with the control law obtained by the proposed algorithm
By applying the proposed LMI-based Genetic
algorithm the following values of the three degrees
of freedom are obtained
S = 2.1663 T = 1.2036 d = 2.4998
The corresponding guaranteed cost control law
is:
() ()
txtu
⎥
⎦
⎤
⎢
⎣
⎡
=
∧
1.8963-0.3127-1.59561.2727
3.88762.4866 0.6334 2.5665-
The guaranteed cost obtained by the proposed
method is lower than those of the previous methods
(Kosmidou, 1996, Fischman, 1996), and it is more
close to the optimal one, as illustrated in the
following Table 1. For the computation of the
guaranteed cost, equation (7) is used with initial
condition
[
]
′
= 1111
0
x
Table 1: Guaranteed cost and gain norms for the case of
the three methods
Method
Guaranteed
Cost
Norm of the gain
Proposed 4.8978 5.7141
Fischman’s 5.8000 3.0400
Kosmidou’s 5.2591 4.4038
Optimal
Control
3.4890 2.0545
In Figure 3, the landscape of the proposed
genetic algorithm is presented in three cross
sections. The combination of these three landscapes
consists the entire search space of the algorithm.
Also, in Figure 4, the poles of open system and
the closed loop system, for a range of uncertainties
(|a
i
(t)|
≤
1, |b
i
(t)|
≤
1) applying the control law derived
by using the proposed method and the method of
(Fischman, 1996) are depicted. As can be seen, by
this figure, the open system is unstable, while in the
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
332

case of the proposed law, is more stable than the one
obtained by (Fischman, 1996).
Finally, the state responses of the closed
systems, in the case of the proposed law and the
(Fischman, 1996) one, are presented in Figure 5.
This figure points, that the proposed gain feedback,
behaves quite more efficiently than the other, since
the responses are smoother.
(a)
(b)
Figure 5: State responses (a) proposed method and (b)
Fischman’s method
6 CONCLUSIONS
A novel method of finding a robust control law, that
guarantees an upper bound of a quadratic
performance index, has been presented in this paper.
The proposed method is based on the
combination of the Genetic Algorithms and the LMI
optimization tool (Gahinet, 1995). It makes use of an
LMI approach to the guaranteed cost, presented in
(Fischman, 1996), of the form of an objective
computation method.
The LMI proposed in (Fischman, 1996), is
modified to find only an optimal matrix P, while the
rest of free parameters are derived through a
genetically processed algorithm.
The results are very promising, since the resulted
guaranteed cost is lower than previous ones
(Kosmidou, 1996, Fischman, 1996),
with an
additional quite better system behavior, in the sense
of stability.
REFERENCES
Coley D.A., 2001. “An Introduction to Genetic
Algorithms for Scientists and Engineers”, World
Scientific Publishing.
Fischman A., Dion J.M., Dugard L. and Trofino Neto A.,
1996. “A Linear Matrix Inequality Approach for
Guaranteed Cost Control”, IFAC World Congress, San
Francisco-USA.
Gahinet P., Nemirovski A., Laub A.J., Chiladi M., 1995.
“LMI Control Toolbox”, The Mathworks Partner
Series.
Holland J.H., 2001. “Adaptation in Natural and Artificial
Systems”, MIT Press.
Kosmidou O.I., Abou-Kandil H., Bertrand P., 1991. “A
Game Theoritic Approach for Guarantedd Cost
Control”, European Control Conference (ECC1991),
pp. 2220-2225, Grenoble-France.
Kundu S., Kawata S., 1996. “Genetic Algorithms for
Optimal Feedback Control Design”, Artif. Intell. Vol.
9, No. 4, pp. 403-411.
AN LMI-BASED GENETIC ALGORITHM FOR GUARANTEED COST CONTROL
333
