USING A DISCRETE-EVENT SYSTEM FORMALISM FOR THE

MULTI-AGENT CONTROL OF MANUFACTURI

NG SYSTEMS

Guido Maione

DIASS, Politecnico di Bari, Viale del Turismo, 8, 74100, Taranto, Italy

David Naso

DEE, Politecnico di Bari, Via Re David, 200, 70125, Bari, Italy

Keywords: Multi-Agent Systems, Discrete Event Dynamic Systems, Distributed Manufacturing Control, Heterarchical

Manufacturing Systems

Abstract: In the area of Heterarchical Manufacturing Systems

modelling and control, a relatively new paradigm is that

of Multi-Agent Systems. Many efforts have been made to define the autonomous agents concurrently

operating in the system and the relations between them. But few results in the current literature define a

formal and unambiguous way to model a Multi-Agent System, which can be used for the real-time

simulation and control of flexible manufacturing environments. To this aim, this paper extends and develops

some results previously obtained by the same authors, to define a discrete event system model of the main

distributed agents controlling a manufacturing system. The main mechanism of interaction between three

classes of agents is presented.

1 INTRODUCTION

Nowadays, the study of appropriate tools for

modelling and designing Multi-Agent Systems

(MAS) technologies is a key-issue involving all their

application areas, including telecommunication and

computer networks, communities of intelligent

robots, web-based agents for information retrieval,

to mention a few. Moreover, considerable research

efforts have been devoted to the definition of

standards and to the development of platforms for

unambiguous agent specification, especially in the

context of software engineering.

Focusing on the specific con

text of industrial

manufacturing, this paper proposes an approach

based on the Discrete EVent System (DEVS)

specification (Zeigler et al., 2000) to obtain a

complete and unambiguous characterization of a

multi-agent control system. By using the DEVS

formalism, we describe agents as atomic dynamic

systems, subject to external inputs from (and

generating outputs to) other agents. Furthermore, we

directly obtain the model of the entire network of

agents by specifying the relationships between the

atomic agents. The DEVS technique is fully

compatible with the heterarchical design principles,

and leads to MAS where all information and control

functions are distributed across autonomous entities.

In particular, the DEVS formalism is an interesting

alternative to other recently proposed tools for MAS

specification, e.g. the UML (Huhns and Stephens,

2001), Petri Nets (Lin and Norrie, 2001). The

success of this formalism is due to its suitability for

developing useful models both for discrete event

simulation, and for implementation of the software

controllers on plant’s operating system. Namely, the

DEVS formalism can effectively model many recent

MAS architectures, such as part-driven heterarchical

manufacturing systems (Duffie and Prabhu, 1996,

Prabhu and Duffie, 1999) and schemes inspired by

the Contract Net protocol (Smith, 1980, Parunak,

1994, Sousa and Ramos, 1999).

As in most MAS for manufacturing control

(

Heragu, 2002, Shen and Norrie, 1999), in our

model all the agents use decision algorithms

emulating micro-economic environments. Each

agent uses a fictitious currency to buy services from

other seller agents which, on their turn, use pricing

strategies. Sellers and buyers have to reach an

equilibrium between conflicting objectives, i.e. to

maximize profit and to minimize costs, respectively.

Maione G. and Naso D. (2004).

USING A DISCRETE-EVENT SYSTEM FORMALISM FOR THE MULTI-AGENT CONTROL OF MANUFACTURING SYSTEMS.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 84-91

DOI: 10.5220/0001145400840091

 SciTePress

Recently, there have been efforts to develop

analytical models of negotiation processes using, for

instance, Petri nets (Hsieh, 2004), underlining the

need of a systematical analysis and validation

method for distributed networks of autonomous

control entities. Many other researches have focused

on the experimental validation of MAS on

distributed simulation platforms (Shattenberg and

Uhrmacher, 2001, Logan and Theodoropoulos,

2001), which allow to perform detailed

investigations on the interaction schemes. Sharing

the same motivations with the mentioned researches,

our work focuses on the development of DEVS

models of MAS, which combines the rigor of a tool

suitable for performing the theoretical analysis of

structural properties of the MAS, with its efficiency

in directly translating the model in a detailed

simulation environment, and its flexibility in testing

both the individual and collective dynamics of the

autonomous entities. Namely, our main goal is to

find a multi-agent design platform that allows users

to assess the relative effectiveness of agents’

decision and interaction strategies, with special

interest to adaptive learning mechanisms that allow

agents to improve their performance during their

operation (Maione and Naso, 2003a).

In this paper, we develop a detailed model of the

interactions between the main agents in a

manufacturing system. This contribution extends

previous researches by the authors, in which, for

sake of simplicity, the interactions with transport

units were not considered in detail, and illustrates

the basic mechanisms of the modelling procedure.

The paper also outlines other main directions of the

research in progress. Section 2 introduces the basic

components of the proposed MAS, and specifies

their roles and relations. Section 3 specifies how to

model agents as atomic DEVS. Section 4 focuses on

the main interactions between agents, describing the

negotiation for a manufacturing process on a part.

Sections 5 and 6 give some experimental results,

overview the advantages of the approach, and

enlighten the issues open for further research.

2 THE MULTI-AGENT SYSTEMS

CONTROL APPROACH

We consider each Part Agent (PA) as a control unit

connected to the corresponding physical part (piece)

flowing through the system. In accordance with the

related literature (Duffie and Prabhu, 1996, Heragu,

2002, Prabhu and Duffie, 1999), we associate each

part into a batch of identical items in process with a

PA that identifies in real-time (i.e. shortly before a

part is ready for a new process) the most suitable

workstation for the imminent operation on that part

and, consequently, the most suitable vehicle to

transfer it to the station. The selection is based on

real-time updated information directly received from

the alternative stations and transport vehicles,

through an exchange of messages with other agents.

Namely, a Workstation Agent (WA) is a software

entity controlling a workstation or a cell of machines

performing the same operations, and a Transport

Agent (TA) is associated with the transport system

or with a single or group of transport units.

At each operation step, by interacting with WAs

and TAs, a PA chooses the machine servicing the

associated part and the transport device moving the

piece from its current position (the output buffer of

the occupied machine) to the chosen workstation.

In this framework, one can consider also specific

agents designed to execute other tasks necessary for

the global operation of the manufacturing plant

(Maione and Naso, 2003b). In particular, one can

associate an Order Agent (OA) with each different

order issued by the management level. The OA

retains information on quantity and type of products

to be processed. Similarly, one can define a Loading

Agent (LA) to manage the loading/unloading station

where the raw/completed parts enter/exit the system.

The global control of the manufacturing floor

emerges from the concurrent actions of the various

agents in the system. The careful analysis of their

interactions is fundamental to understand how to

obtain the desired global behaviour. For instance, the

OA interacts with PAs to control the release of the

quantity and type of raw parts necessary to realize

that order. The PAs interact with the LA to negotiate

the loading/unloading of raw/completed parts. Here,

we concentrate on the interactions between a PA and

WAs and TAs when a part is ready for a new

process and its PA has to decide the resources

(workstation and transport device) necessary to fulfil

the operations, among a set of available alternatives.

The high-level agents’ decisions are executed by

low-level plant controllers that are not modelled

here. One can also view the network of interacting

agents as a distributed controller supervising and

synchronizing the underlying physical hardware.

3 THE DISCRETE-EVENT

MODELLING FRAMEWORK

The agents operating in our MAS model interact one

with another by exchanging event messages. Outputs

from an agent become inputs for other agents. The

agent state is updated by external input events

(inputs) and internal events. Each event in the life of

an agent is considered an instantaneous or “atomic”

USING A DISCRETE-EVENT SYSTEM FORMALISM FOR THE MULTI-AGENT CONTROL OF

MANUFACTURING SYSTEMS

action without duration. Time-consuming actions are

represented by a pair of events, the first denoting its

start and the second denoting its finish.

So, unambiguous models for the agents in the

system are identified by all the classified events

which affect the dynamics of each type of agent. The

internal events are generated by the internal

dynamics of the agent, and the exogenous events are

inputs which are not determined by the agent.

Finally, the external output events (or outputs)

represent the reaction of the agents. Then, it is

important to define the sequential state of each

agent. Namely, events change the state. An agent

stays in a state until either it receives an input, or an

amount of time determined by a time advance

function elapses. In the latter case, an internal event

occurs to change state according to a specified

internal transition function. Otherwise, if an agent

receives an input, an external transition function

specifies the state transition according to the current

total state of the agent, defined by the sequential

state, the time elapsed since the last transition and

some additional information. Finally, agents

generate outputs according to an output function.

Delays and faults in the communication process are

also considered in our model. Although the effects

of these phenomena are often neglected in technical

literature, we evaluate their effects both on overall

production performance and on the efficiency of the

MAS, expressed by ad-hoc performance measures.

This allows us to track, monitor and optimize the

interaction among agents.

To conclude, each agent may be modeled as an

atomic DEVS as follows:

A = < X, Y, S,

int

ext

, ta > (1)

where X is the set of inputs, Y is the set of outputs, S

is the set of sequential states,

int

: S→S is the

internal transition function,

ext

: Q×X→S is the

external transition function,

: S→Y is the output

function, ta: S→ℜ

is the time advance function

(ℜ

set of positive real numbers with 0 included),

Q = {(s,e,DL) | s∈S,0≤e≤ta(s)} is the total state set.

The sequential state s contains the main

information on the status, specifying the condition

of an agent between two successive events. Other

data strictly depend on the type of the agent. E.g.,

for a PA, one can consider the current residual

sequence of operation steps necessary to complete

the procedure, the set of available machines for the

negotiated operation, and prospected time in current

state before the next internal event. For a WA, s

includes the queues of the requests received from

PAs for availability, information and confirmation of

negotiated operations (see below), and the time

before the next internal event. For a TA, s may

contain similar queues of requests received from

PAs, and the time before the next internal event.

The total state q depends on s, the time e elapsed

since the last transition and the decision law DL

used by the agent to select and rank the offers

received from other agents and to decide its action.

Usually, to build the models, one observes that

each agent may require or offer a service to other

agents. A precise mechanism usually defines the

negotiation protocols working according to a cycle

“announce-offer-reward-confirm”: an agent starts a

bid by requiring availability for a service to one or

more agents, requests the available agents

information representing an offer for the negotiated

service, collects the replies from the queried agents,

selects the best offer, sends a rewarding message,

waits for a confirmation and finally acquires the

service from the rewarded agent.

In this paper, we focus on the interactions of a

PA with WAs and TAs when contracting for an

operation in the procedure to be accomplished for a

part in process. We describe the main part of the PA

DEVS model, by concentrating on the mechanism

ruling the status-transitions of a PA, which are

triggered by inputs or internal events, and the

outputs generated for each status. We don’t go into

the details of the DL used by each agent. To this

aim, we exploit the models already defined and

developed in precedent papers (Maione and Naso,

2003a,b) for PAs, WAs and TAs, but we expand and

better clarify them to put them together.

4 THE INTERACTIONS OF A PA

WITH WAS AND TAS

To accomplish the manufacturing tasks, each PA

interacts with WAs to choose the workstation for the

next operation and with TAs to select the vehicle

moving the part from the station currently occupied

to the next one. We assume that the PA firstly

communicates exclusively with WAs, then with TAs

only.

For t<t

let the PA associated with a generic

part, say P, be in a quiescent status (QUIESC) and

let it begin its activity at t

(event X

). Then P

spends the interval [t

, t

] to send outputs Y

P01

P02

,…, Y

P0w

at instants t

, t

,…, t

. These

messages request the availability to all the WAs of

the alternative stations (w in number) that can serve

the part. The sequence of requests cannot be

interrupted by any internal or external occurrence.

For sake of simplicity, instead of modelling a

sequence of w status-values, we refer to REQWAV

for the whole duration of the activity and assume

that P makes transition at t

(event I

In [t

, t

] P waits for answers (WAIWAV).

Namely, the request P transmits to each WA may

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

queue up with similar ones sent by other PAs. Next

transition occurs at t

when either P receives all the

answers from the queried WAs (X

), or a specified

time-out of WAIWAV expires before P receives all

the answers. In case it receives no reply within the

timeout (I

), P returns to REQWAV and repeats the

request procedure. In case of time-out expiration and

some replies received (I

), P considers only the

received answers to proceed. The repeated lack of

valid replies may occur for system congestion, for

machine failures or communication faults, or for

other unpredictable circumstances. In all cases

permanent waits or deadlocks may occur. To avoid

further congestion and improve system fault-

tolerance, we use time-outs and let P repeat the

cycle REQWAV-WAIWAV only a finite number of

times, after which P is unloaded from the system.

If all or some replies are received before the

time-out expiration, P starts requesting service to the

m≤w available WAs at t

. In [t

, t

] P requests

information to these WAs by sending them Y

P11

P12

, …, Y

P1m

at instants t

, t

,…, t

. If the

sequence of requests cannot be interrupted, we refer

to REQWSE for the whole activity. We assume that

at t

P makes transition (I

Then, P spends [t

, t

] waiting for offers from

the available WAs (WAIWOF), as the request P

transmits to each WA may queue up with those sent

by other PAs. Next transition occurs at t

when

either P receives all the answers from the queried

WAs (X

) or a time-out of WAIWOF expires. In

case it receives no reply within the timeout (I

), P

returns to REQWSE and repeats the procedure. In

case of time-out expiration and some replies are

received (I

), P considers only the received offers to

select the next server. Again, to avoid congestion, P

repeats the cycle REQWSE-WAIWOF a finite

number of times, then it is discharged.

Once received the offers from WAs, P utilizes

, t

] to take a decision for selecting the

workstation (TAKWDE). At t

the decision

algorithm ends (I

), after selecting a WA and

building a queue to rank all the offers of other WAs.

Subsequently, P reserves the chosen machine by

transmitting a booking message (Y

) to the

corresponding WA. So P takes [t

, t

] for

communicating the choice to the WA (COMCHW).

At t

the communication ends (I

). Now, the WA

has to send a rejection if there is a conflict with

another PA or a booking confirmation (X

). Hence,

P uses [t

, t

] to wait for a confirmation from the

selected WA (WAIWCO). The confirmation is

necessary because during the decision interval the

condition of the plant can be modified by actions of

other PAs, and the selected server can be no longer

available. If P receives a rejection (X

), or does not

receive any reply within a time-out (I

), it returns to

COMCHW, sends a new request of confirmation to

the second WA in the decision rank. If P has no

other alternative destinations and the rejection (X

)

or the time-out (I

P10

) occurs, it returns to REQWAV

and repeats the negotiation. Also WAIWCO,

WAIWAV and WAIWOF cannot lead to deadlocks,

thanks to the time-out.

At t

, after receiving a confirmation from the

selected WA, P starts the negotiation with TAs for a

device to carry the part from the current position to

the input buffer of the selected workstation, where

the last negotiated operation is to be made. Then P

opens the bid and spends [t

, t

] to send Y

P31

, Y

P32

…, Y

P3v

at instants t

, t

,…, t

to all the v

possible TAs to request their availability

(REQTAV). In [t

, t

] after the end of transmission

P11

), P waits for availability-answers (WAITAV)

until a time-out expires: if no reply is received, P

gets back to REQTAV (I

P12

) to repeat the request.

Otherwise, if all replies are received before the time-

out expiration (X

) or u≤v replies are received and

the time-out expires (I

P13

), at t

P starts requesting

service to the u available TAs (REQTSE).

Then P uses [t

, t

P10

] to send outputs Y

P41

, Y

P42

…, Y

P4u

at instants t

, t

,…, t

P10

to all the

available TAs and, after the transmission is

completed (I

P14

), P waits for offers from TAs

(WAITOF) in [t

P10

, t

P11

] until a time-out expires. If

no offer is received (I

P15

), the PA repeats the request.

If only some offers arrive and the time-out expires

P16

) or all offers arrive before the time-out (X

), P

can take a transport-decision (TAKTDE) for

selecting the best offering TA in [t

P11

, t

P12

]. After

selection (I

P17

), in [t

P12

, t

P13

] P communicates its

choice by sending Y

to this TA (COMCHT). After

this communication (I

P18

), P waits for a rejection or

a confirmation from the selected TA (WAITCO)

until a time-out expires. If no reply is received in the

waiting period [t

P13

, t

P14

] and a time-out expires (I

P19

)

or a rejection is received (X

), in case other offers

from TAs are available P gets back to COMCHT

and selects a new TA; in case no other TA is

available and there is a time-out expiration (I

P20

) or a

rejection (X

), the availability request is repeated

and P gets back to REQTAV.

If a confirmation is received (X

P10

), P makes a

transition to issue a transport command (TRANSP).

It takes the interval [t

P14

, t

P15

] to issue the command

to load the part on the vehicle associated with

the selected TA and to start the transport process.

When, at time t

P15

, the command is complete (I

P21

P gets back to QUIESC. In case of the last

operation, Y

also signals the completion of the

working procedure to a controller, which influences

and adapts the DL the PA uses for ranking the offers

(Maione and Naso, 2003a). In this case, P leaves the

system.

USING A DISCRETE-EVENT SYSTEM FORMALISM FOR THE MULTI-AGENT CONTROL OF

MANUFACTURING SYSTEMS

In general, from t

P15

to the beginning of the next

operation (if any), P stops making decisions,

receiving and sending messages and remains

quiescent. The associated part is loaded on the

transport vehicle and transferred to the next

workstation where it is downloaded in the input

buffer. Here, it waits in queue until receiving

service, after a proper set-up. After the operation, the

part reaches the output buffer and is ready for the

next destination. All the above processes are driven

by low-level controllers and do not involve agent

activities. So, only when the processes are over, P is

again ready to start a new negotiation phase. If for

t>t

P15

faults occur to the selected machine or vehicle,

P remains in QUIESC and there is no need to restart

negotiations with WAs or TAs. In fact, the plant

controllers manage the repair process: when the

normal operating conditions are restored, the part is

transported to the selected machine.

Note that, after the negotiation cycle is complete,

when the chosen and confirmed WA (or TA) signals

to the PA the end of the operation (or transport)

process, the PA can take into account its new

availability. If, at this time, the PA is requesting or

waiting for availability or information from other

WAs (or TAs), or is taking a decision for operation

(transport) on other parts, the received messages

from the past-selected WA (or TA) wait in a queue

until the PA gets to REQWSE (or REQTSE). In this

case, the PA will send an output Y

P1m+1

(or Y

P4u+1

)

also to this new available WA (TA).

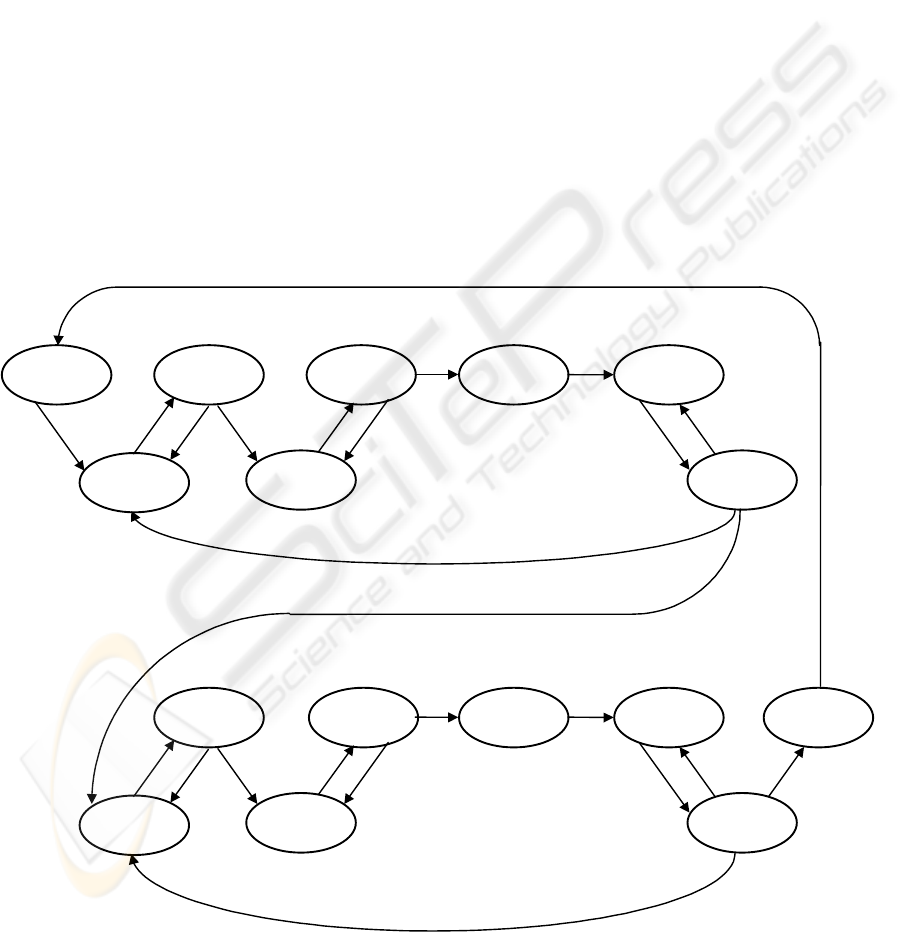
Figure 1 depicts all this complex interaction

dynamics. Circles represent the PA status-values,

arrows represent the events, and the outputs, directly

associated with status-values, are encapsulated into

the circles. As the figure shows, the PA may receive

confirmation from a WA (or a TA) after several

successive couples COMCHW-WAIWCO (or

COMCHT-WAITCO). Also, time-outs can bring the

PA back to REQWAV (from WAIWAV when no

answer is received from WAs or from WAIWCO

after a WA-rejection) or to REQTAV (from

WAITAV when no answer is received from TAs or

from WAITCO after a TA-rejection).

)

QUIESC

P21

P15

)

P18

P13

)

/ I

P20

P14

)

P14

, t

P15

]

)

/ I

P10

)

/ I

)

, t

] [t

, t

]

, t

]

, t

]

, t

] [t

P10

, t

P11

] [t

P11

, t

P12

] [t

P12

, t

P13

]

P13

, t

P14

]

COMCHT

P10

P14

)

/ I

P19

P14

)

WAITCO

TRANSP

WAITAV

, t

P10

]

/ I

P13

)

REQTSE

P41

…Y

P14

P10

)

P15

P11

)

P17

P12

)

/ I

P16

P11

)

TAKTDEWAITOF

P12

)

P11

)

, t

]

REQTAV

P31

…Y

P3v

, t

]

REQWSE

P11

…Y

)

, t

]

REQWAV

P01

…Y

P0w

/ I

)

, t

]

WAIWCO

COMCHW

)

/ I

)

TAKWDEWAIWOFWAIWAV

Figure 1: dynamics of a PA when negotiating with WAs and TAs.

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

On one hand, one could simplify the model by

merging REQWAV, WAIWAV, REQWSE and

WAIWOF, i.e. by considering the PA sending

requests for availability and information all together.

So, each WA would offer availability and the

information necessary to the PA decision at the same

time. Only two status-values would be necessary,

the first for the request, the second for the wait. The

same reduction is possible for REQTAV, WAITAV,

REQTSE and WAITOF.

On the other hand, the more detailed model of

the PA activities, which considers two different

time-outs for the two different waiting conditions

previously defined, can be more effective in

reducing the PA waiting times and in avoiding

deadlocks. In fact, the effect of delays and losses of

messages due to workstation or transport

unavailability (faults, malfunctions, overloaded

workstations, etc.) and to communication faults are

reduced. Also, the cyclic repetition of requests and

waits and the consequent delays in the decision

processes are limited. As a consequence, the risk of

discharging PAs from the system is reduced.

To better enlighten the negotiation mechanism,

we summarize in Tables I-III the status-values,

inputs, internal events and outputs.

Table I: status-values for a Part Agent

Status Agent’s Activity Description

QUIESC Agent inactive

REQWAV Request availability to all possible WAs

WAIWAV Wait for availability signal from WAs

REQWSE Request service to available WAs

WAIWOF Wait for offers from available WAs

TAKWDE Take decision for the best WA offer

COMCHW Communicate choice to selected WA

WAIWCO Wait confirm./reject. from selected WA

REQTAV Request availability to all possible TAs

WAITAV Wait for availability signal from TAs

REQTSE Request service to available TAs

WAITOF Wait for offers from available TAs

TAKTDE Take decision for the best TA offer

COMCHT Communicate choice to selected TA

WAITCO Wait confirm./reject. from selected TA

TRANSP Command selected TA to move the part

Figure 1 shows that the negotiation mechanism

maintains a well defined structure with other agents

participating to a negotiation process.

In a similar way, a DEVS model can be defined

for other interactions between classes of agents

(Maione and Naso, 2003b). The common structure

of the negotiation mechanism is advantageous for

building up complex models in a modular way.

The DEVS model of the agents’ interactions is

particularly suitable for developing a complete

simulation platform for the analysis of the dynamics

of the complex MAS controlling a manufacturing

plant. In particular, our model allows the simulation

of both the plant processes and their macroscopic

hardware components (machines, AGVs, parts, etc.),

and the details of the control activities performed by

agents (inputs, outputs, states, time-outs). So, we can

evaluate the classical indices of a manufacturing

system performance (throughput, number of

completed items, lateness, etc.), but also the effects

of agents and their decision policies and the MAS

efficiency (number of negotiation cycles, number of

requests). Also, we can measure the agents’ behavior

in steady-state operating conditions and their

adaptation to abrupt disturbances (shortages of

materials, workload changes, hardware faults, etc.).

In this sense, we made all these measures when

agents were using different decision policies, to see

how they dynamically react to disturbances (Maione

and Naso, 2003a,c). We compared other MAS that

use conventional decision heuristics (based on the

delivery time of parts to machines, the distance to

the next workstation, the required set-up time) with

our MAS, both with and without adaptation. We let

agents use a set of decision rules for a limited

amount of time (the agent life-cycle) and then we

replace the rules by using the most successful ones.

The replacement at the end of life-cycle was guided

by a mechanism emulating the ‘survival of the

fittest’ natural selection process and propagating the

fittest rules to the next population of agents. The

fitness of each decision rule was the average lateness

of the parts controlled (Maione and Naso, 2003a).

Table II: inputs received and outputs sent by a PA when negotiating with WAs and TAs

Inputs Time Description

Outputs Description

Start negotiation for a new operation

P01

P02

… Y

P0w

Requests of availability

Last reply for WA availability received

P11

P12

… Y

P1m

Requests of service to available WAs

Last reply for WA offer received

Choice communication to the selected WA

Rejection & alternative WAs in the PA rank

P31

P32

… Y

P3v

Requests of availability TAs

Rejection & no alternative WA in the PA rank

P41

P42

… Y

P4u

Requests of service to available TAs

Confirmation from a WA

Choice communication to the selected TA

Last reply for TA availability

Transport command

P11

Last reply for TA offer

P14

Rejection & alternative TAs in the PA rank

P14

Rejection & no alternative TA in the PA rank

P10

P14

Confirmation from a TA

USING A DISCRETE-EVENT SYSTEM FORMALISM FOR THE MULTI-AGENT CONTROL OF

MANUFACTURING SYSTEMS

Table III: internal events of a PA when negotiating with WAs and TAs

Internal Event Time Description

End of WA availability request process

Time-out and no availability signal received from WAs

Time-out and some (m) availability signals received from WAs

End of WA service request process

Time-out and no offer received from the m available WAs

Time-out and some offers (o<m) received from the available WAs

End of workstation-decision process

End of choice communication to the selected WA

Time-out and no confirmation received from the selected WA when other ranked WA offers are available

P10

Time-out and no confirmation received from the selected WA when no other ranked WA offers are available

P11

End of TA availability request process

P12

Time-out and no availability signal received from TAs

P13

Time-out and some (u) availability signals received from TAs

P14

P10

End of TA service request process

P15

P11

Time-out and no offer received from the u available TAs

P16

P11

Time-out and some offers (o<u) received from the available TAs

P17

P12

End of transport-decision process

P18

P13

End of choice communication to the selected TA

P19

P14

Time-out and no confirmation received from the selected TA when other ranked TA offers are available

P20

P14

Time-out and no confirmation received from the selected TA when no other ranked TA offers are available

P21

P15

End of transport command

5 SOME EXPERIMENTAL

RESULTS AND FUTURE PLANS

The DEVS model is particularly suitable for

developing a simulation platform for the analysis of

the complex dynamics of distributed multi-agent

control systems. Differently from traditional discrete

event models of manufacturing plants, mainly

devoted to simulate the macroscopic components,

our model considers also the detailed dynamics of

the software agents (exchanged event messages,

internal events and outputs). In this way, we may

study also the effects of hardware faults, congestion

of the communication network, message losses or

similar circumstances.

For instance, it is possible to compare various

decision policies used by the various agents to

negotiate operations in a detailed simulation model,

as done in (Maione and Naso, 2003a).

The simulation model also allows us to perform

comparative analysis in dynamic conditions, and

define reactive policies that minimize the effects of

disturbances, e.g. a workstation fault. For example

Figure 2 compares four different agents’ decision

policies by throughput: minimizing the distance

between consecutive workstations (A), minimizing

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

x 10

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

Com parison by Average Throughput

tim e [s ]

Throughput [parts/min]

D [8]

Figure 2: comparison of performance in dynamic conditions (workstation fault at t = 1 0^5 s).

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

the wait for set-up of the workstation (B),

minimizing the wait in queue at the workstation (C),

and using a learning strategy (D). It can be noted

how the reactive policy (D), designed with the aid of

the DEVS model, outperforms the common (static)

decision rules using MAS.

Future research aims at applying the proposed

approach to other complex distributed control and

optimization problems, such as those involved in

large-scale logistic or supply chains.

6 CONCLUDING REMARKS

In this paper, we used the DEVS formalism to

specify the model of the main agents operating in a

MAS controlling part-driven heterarchical

manufacturing systems. In this context, we detailed

the interactions guiding the negotiations related to a

generic step in a working procedure associated with

a part process. The model respects heterarchical

principles and can be used in a simulation platform

which allows us to analyze both the classical

performance indices of a manufacturing system and

the effectiveness of the MAS, using decision

policies which implement adaptation strategies.

The proposed method leaves many interesting

issues open for further research. The next step

toward the experimentation of the multi-agent

control system on an automated manufacturing

plant, is to test the DEVS model on a distributed

network of computers, each hosting one or more of

the agents in the heterarchical network. This aims at

investigating and properly addressing the critical

issues related to distributed autonomous controllers

that cannot be examined when simulating the whole

set of agents on a centralized platform.

REFERENCES

Duffie, N.A., Prabhu, V.V., 1996. Heterarchical control of

highly distributed manufacturing systems.

International Journal of Computer Integrated

Manufacturing, Vol. 9, No. 4, pp. 270-281.

Han, W., Jafari, M.A., 2003. Component and Agent-Based

FMS Modeling and Controller Synthesis. IEEE Trans.

Sys., Man, and Cybernetics – Part C, Vol. 33, No. 2,

pp. 193-206.

Heragu, S.S., Graves, R.J., Kim, B.-I., Onge, A.St., 2002.

Intelligent Agent Based Framework for Manufacturing

Systems Control. IEEE Trans. Sys., Man, and Cyber. -

Part A, Vol. 32, No. 5.

Hsieh, F.-S., 2004. Model and control holonic

manufacturing systems based on fusion of contract

nets and Petri nets. Automatica, 40, pp. 51-57.

Huhns, M.N., Stephens, L.M., 2001. Automating supply

chains. IEEE Int. Comput., Vol. 5, No. 4, pp. 90-93.

Kotak, D., Wu, S., Fleetwood, M., Tamoto, H., 2003.

Agent-based holonic design and operations

environment for distributed manufacturing. Computers

in Industry, 52, pp. 95-108.

Lee, J.S., Hsu, P.L., 2004. Design and Implementation of

the SNMP Agents for Remote Monitoring and Control

via UML and Petri Nets. IEEE Trans. Control Sys.

Techn., Vol. 12, No. 2, pp.293-302.

Lin, F., Norrie, D.H., 2001. Schema-based conversation

modeling for agent-oriented manufacturing systems.

Computers in Industry, Vol. 46, pp. 259-274.

Logan, B., Theodoropoulos, G., 2001. The distributed

Simulation of Multiagent systems. Proceedings of the

IEEE, Vol. 89, No.2, pp. 174-185.

Maione, G., Naso, D., 2003a. A Genetic Approach for

Adaptive Multi-Agent Control in Heterachical

Manufacturing Systems. IEEE Trans. Sys., Man, and

Cyb. – Part A: Spec. Issue Collective Intelligence in

Multi-Agent Systems, Vol. 33, No. 5, pp. 573-588.

Maione, G., Naso, D., 2003b. A Discrete-Event System

Model for Multi-Agent Control of Automated

Manufacturing Systems. In IEEE SMC’03, Int. Conf.

on Sys., Man and Cyb., Washington D.C., USA.

Maione, G., Naso, D., 2003c. A Soft Computing Approach

for Task Contracting in Multi-Agent Manufacturing

Control. Comp. Ind., Vol. 52, No. 3, pp. 199-219.

Parunak, H.V.D., 1994. Applications of Distributed

Artificial Intelligence in Industry. In O’Hare,

Jennings, (Eds.), Foundations of Distributed Artificial

Intelligence, Wiley-Inter-Science.

Prabhu, V., Duffie, N., 1999. Nonlinear dynamics in

distributed arrival time control of heterarchical

manufacturing systems, IEEE Trans. Control Systems

Technology, Vol. 7, No. 6, pp. 724-730.

Shattenberg, B., Uhrmacher, A.M., 2001. Planning Agents

in James. Proc. of the IEEE, Vol. 89, No. 2, pp. 158-

173.

Shen, W., Norrie, D.H., 1999. Agent-Based Systems for

Intelligent Manufacturing: A State-of-the-Art Survey,

Knowledge and Information Systems, an International

Journal, Vol. 1, No. 2, pp. 129-156.

Smith, R.G., 1980. The Contract Net Protocol: High Level

Communication and Control in a Distributed Problem

Solver. IEEE Trans. Computers, Vol. 29, No. 12, pp.

1104-1113.

Sousa, P., Ramos, C., 1999. A distributed architecture and

negotiation protocol for scheduling in manufacturing

systems. Computers in Industry, Vol. 38, pp. 103-113.

Zeigler, B.P., Praehofer, H., Kim, T.G., 2000. Theory of

Modelling and Simulation, Academic Press, 2nd edit..

USING A DISCRETE-EVENT SYSTEM FORMALISM FOR THE MULTI-AGENT CONTROL OF

MANUFACTURING SYSTEMS