
NEW METHOD FOR STRUCTURAL CHANGE DETECTION OF
TIME SERIES AS AN OPTIMAL STOPPING PROBLEM
Hiromichi Kawano, Ken Nishimatsu
NTT Service Integration Laboratories, Musashino-shi, Tokyo, 180-8585 Japan
Tetsuo Hattori
School of Enginieering, Kagawa University, Takamatsu City, Kagawa, 761-0396 Japan
Keywords: Time series, Structural change, Dynamic Programming, Optimal stopping problem
Abstract: In general, an appropriate pred
iction expression and/or model is constructed to fit a time series though, the
model begins to unfit (or not to fit) the time series from some time point, especially in the field that relates
to human activity and social phenomenon. In such case, it will be important not only to quickly detect the
unfitting situation but also to rebuild the prediction model after the detection as soon as possible. In this
paper, we formulate the structural change detection problem in time series as an optimal stopping problem,
using the concept of DP (Dynamic Programming) with a cost function that is the sum of unfitting (or not
fitting) loss and action cost to be taken after detection. And we propose a method for optimal solution and
show the correctness by proving a theorem. Also we clarify the effectiveness by showing the numerical
experimentation.
1 INTRODUCTION
Change point detection (CPD) problem in time series
is to find that a structure of generating data has
changed at some time point by some cause. We
consider that the problem is very important and that
it can be applied to a wide range of application
fields.
For example, degradation detection in
com
munication system (R.Jana and S.Dey, 2000),
object detection on a radar screen ( R.M.Gagliardi
and I.S.Reed, 1965), speech processing (R.J.Di
Francesco, 1990), and fault detection (A.S.Willsky,
1996), (D.Kauame, et al., 1996) are such application
examples of the CPD problem.
The processing method for the CPD problem is
ro
ughly divided into two types: one is batch
processing that checks all generated data in the past
and another is sequential processing that checks if
the structure has changed or not at every new data
generation.
As the former representative method, Chow test
is well kn
own and is often used in econometrics
(Chow,G.C., 1960). It does a statistical test by
setting the hypothesis that the change has occurred at
time t. However, the problem of Chow test exits in
that we have to give the change time t for the
hypothesis setting, and also in that the test lacks the
rapidity to detect the change point.
As the latter representative method, there are
B
ayes’ method (S.MacDougall, A.K.Nandi and
R.Chapman, 1998), (V.V.Veeravalli and
A.G.Tartakovsky, 2002) and CUSUM one
(E.S.Page, 1954), (C.Han, P.k.Willet and
D.A.Abraham, 1999), (S.D.Blostein, 1991), (Y.Liu
and S.D.Blostein, 1994), (M.Basseville and
I.V.Nikiforov, 1993), (M.Basseville, 1988), based on
sequential probability ratio test. The Bayes’ method
can detect the change point, based on the sequential
estimation of posterior probability, if the generation
distribution of time series data is known at the time
before and after the change point. So the Bayes’
method can solve the problem in the Chow test, but
it requires that the generation distribution for the
time series data is already known.
24
Kawano H., Nishimatsu K. and Hattori T. (2004).
NEW METHOD FOR STRUCTURAL CHANGE DETECTION OF TIME SERIES AS AN OPTIMAL STOPPING PROBLEM.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 24-31
DOI: 10.5220/0001147500240031
Copyright
c
SciTePress

Moreover, in practical situation, we have to
consider not only that a loss cost is involved with
prediction error but also that an action to be taken
after the change detection will need a cost.
Conversely, the CPD is necessary in order to judge
when to take the action.
Taking the field of network management for
example, time series data (e.g. error rate and delay)
of the quality are always monitored, and when the
structural change is detected, some action for the
quality improvement is taken.
In the structural change detection under such
situations, we must consider the trade-off between
loss by the degradation and cost for the quality
reformation.
However, as far as the authors can know, no
such conventional CPD method considering the
action cost has been proposed, in spite of the fact
that such method is very useful at practical level.
In this paper, in order to solve difficulties in
conventional methods for structural change detection
in time series, we propose a new and practical
method based on an evaluation function of loss cost.
And we formulate the CPD problem as an optimal
stopping problem using the concept of DP (Dynamic
Programming) and give the optimum solution in the
formulation. We consider that our method is
effective in the sense as follows.
1. Differently from the Chow test, it does not need to
set the change point in a priori.
2. Unlike the Bayes’ method, it does not need to give
the generation distribution of time series data.
3. It can quickly detect the structural change point by
the sequential processing.
4. It minimizes the evaluation function that sums up
the loss involved with prediction error and action
cost to be taken after the change detection.
5. It is a meta-level method so that we can apply it to
any prediction model in the evaluation function.
Also in this paper, we present the correctness of our
solution by proving a theorem and show the
effectiveness by numerical experimentation results.
2 FORMULATION
2.1 Evaluation Function
We formulate the CPD problem as an optimal
stopping one based on an evaluation function that
sums up the cost involved by prediction error and
action cost to be taken after the change detection.
For example, a prediction expression is given in the
following equation as a function of time t, where y
t
,
β
1
, β0, ε mean the function value, two constant
coefficients, and error term, respectively.
ε
+
β
+
⋅
β
=
01
ty
t
(1)
The error term ε is given as a random variable of the
normal distribution of variance σ and average of 0,
i.e., ε~N(0, σ).
A time series data based on the Equation (1) is
shown in Figure 1, that is generated by making
normal random numbers of average 0 and variance 1
for ε, and by setting β
1
=0.2, β0=1 for the time
t=1,2,…,70, and β
1
=0.8, β0=-41 for the time after
t=71.
The tolerant error interval or tolerance zone between
two broken lines as shown in Figure 1 is decided
using the first time series data from t=1 to t=20.
Using those data, the prediction expression is
made by the least squares method, and the tolerant
interval of error is calculated as 95% confidence
interval of the sample variance of residual ε.
Note that the tolerant error interval is not based
on the confidence interval of regression formula
given in the following Equation (2), but is defined
based on the distribution of error term ε of Equation
(1)(
N.R.Draper, H.Smith, 1996).
xy
10
ˆˆ
β+β=
e
xx
V
S
xx
n
nt
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
++α−±
2
)(1
1),2(
(2)
where t, α ,
x , and n denote t distribution,
significance level, average, and the number of data,
respectively, and let
be prediction error in time
, and are defined as follows.
i
e
i
t
e
V
xx
S
neV
n
i
ie
∑
=
=
1
2
2
1
)(
∑
=
−=
n
i
ixx
xxS
.
0
5
10
15
20
25
30
35
40
45
1 112131415161718191
obser vat ion
dat a
forecasting
dat a
‐2σ
2σ
y
t
Figure 1: Example of time series data.
NEW METHOD FOR STRUCTURAL CHANGE DETECTION OF TIME SERIES AS AN OPTIMAL STOPPING
PROBLEM
25

In Figure 1, it can be read that the generated
data runs out frequently from the tolerance zone
since after t=70. From the fact, when the difference
(or observation error) between the observed data and
forecasted value exceeds a specified tolerance (i.e.,
when the observed data goes out from the tolerance
zone), we can think that that there is a high
possibility that the structural change has occurred.
For simplicity, we think two situations; one is
the situation that the observed data is out from the
tolerance zone, and another the situation that the
observed data is in the zone. Then we call the former
situation “
unfitting” and the latter “fitting”. Based on
this discussion, we consider that the structure has
changed, when the unfitting occurs between
sequentially observed data and forecasted value by
continuing
N times. This specified tolerance is
defined as, e.g., 2σ of the distribution on error ε that
is estimated at the time when the prediction
expression is made.
The evaluation function is given in (3) as the
sum of two kinds of cost: the damage caused by the
unfitting (i.e., unfitting loss) and action cost to be
taken after the change detection.
Total_cost=cost (
A)+cost(n) (3)
where cost(
n) is the sum of the loss by continuing n
times unfitting before the structural change
detection, and cost(
A) is the cost involved by the
action after the change detection.
Taking the quality control problem for example,
the above cost(
n) means the loss caused by the
quality degradation and superfluous quality. And the
cost(
A) means the cost involved by some facility
replacement.
Since the observed time series data is a random
variable and the unfitting event is stochastic, the
value of the evaluation function Total_cost also
becomes a random variable. Then we have to find
the number of times
N that minimizes the
expectation value of Total_cost, under the
assumption that the structural change occurs
randomly. Note that the evaluation function can be
defined if only the distribution of error ε is given, so
there is no need for the prediction expression to be
such a form like equation (1).
2.2 Structural Change Model
We assume that the structural change is Poisson
occurrence of averageλ , and that, once the change
has occurred during the observing period, the
structure does not go back to the previous one. The
reason why we set such a model is that we focus on
the detection of the first structural change in the
sequential processing (or sequential test). The
concept of the structural change model is shown in
Figure 2.
Figure 2: Structural change model
Moreover, we introduce a more detailed model.
Let
R be the probability of the unfitting when the
structure is unchanged. Let
Rc be the probability of
the unfitting when the structure change occurred. We
can consider that
Rc is greater than R, i.e., Rc>R.
The detailed internal model for the State Ec and
E are illustrated as similar probabilistic finite state
automatons in Figure 3 and 4, respectively.
Figure 3: Internal model of the State E.
Figure 4: Internal model of the State E
C.
out
in
1-
R
R
R
E
1-
R
out in
1-
R
c
1-
R
c
R
c
R
c
E
c
1-λ
1.0
E
c
λ
E
Ec : State that the structural change occurred.
E : State that the structure is unchanged.
λ : Probability of the structural change
occurrence. (Poisson Process.)
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
26

2.3 Evaluation Function Using DP
Let the cost(n) be a・n as a linear function for n,
where
a is the loss caused by the unfitting in one
time. And for simplicity, let
C and A denote the
Total_cost and cost(
A), respectively. Then, the
evaluation function in (3) is denoted as the following
equation (4).
naAC ⋅+=
(4)
Using the concept of the DP (Dynamic
Programming), we introduce a function
to
obtain the optimum number of times
n that
minimizes the expectation value of the evaluation
function of Equation (4).
),( NnEC
Let
N be the optimum number. Let the function
be the expectation value of the evaluation
function at the time when the unfitting has occurred
),( NnEC
in continuing
n times, where n is less than or equal to
N, i.e., 0≦ n≦ N. Then the function is
recursively defined as in the following equation.
),( NnEC
(if
n=N )
NaANNEC ・
+
=),(
(5)
(if
n<N )
naSSPNnEC
nn
・・)|(),(
1+
=
),1())|(1(
1
NnECSSP
nn
+−+
+
(6)
where
S
n
is the state of unfitting in continuing n
times,
1+n
S
is the state of fitting for the (n+1)-th
time observed data, and
)|(
1 nn
SSP
+
is the
conditional probability that the state
1+n
S
occurs
after the state
n
The first term in the right-hand side (RHS) of
Equation (6) indicates the expectation value of the
evaluation function at the time when the fitting
happens for the (
n+1)-th time observed data after the
unfitting occurred for continuing
n times.
S
occurred.
The second term in the RHS of Equation (6)
indicates the expectation value of the evaluation
function at the time when the unfitting happens for
the (
n+1)-th time observed data after the unfitting
occurred for continuing
n times.
Note that, from the definition of the function
, the N that minimizes EC(0,N) is the same
as
n that minimizes the expectation value of the
evaluation function of (4).
),( NnEC
2.4 Minimization
For the aforementioned EC(0,N), the following
theorem holds, and gives the
n that minimizes the
expectation value of the evaluation function of (4).
Theorem.
The N that minimizes EC(0,N) is given as the largest
number
n that satisfies the following Inequality (7).
)|()(
1−
+<
nn
SSPaAa ・
(7)
where the number
N+1 can also be the optimum one
that minimizes
EC(0,N), i.e., EC(0,N) = EC(0,N+1)
, only if
)|()(
1 NN
SSPaAa
+
+= ・
.
Proof (Outline).
Since the strict detailed proof needs many pages, we
present the outline of the proof for the Theorem.
In order to prove this Theorem, we derive a
contradiction with two assumptions under a premise
as follows.
Premise: a number
N
′
is the largest number n
that satisfies the Inequality (7).
Assumption 1: There exists a number
N
′
′
such that
'" NN
<
and
)',0()",0( NECNEC <
Assumption 2: There exists a number
N
′
′
such that
"' NN
<
and
),0(),0( NECNEC
′
′
>
′
.
We can derive the above contradiction by three
steps, as described below. At Step 1, we prove the
following fundamental lemmas: Lemma 1-1 and
Lemma 1-2. At Step 2, two lemmas, Lemma 2-1,
and Lemma 2-2, are proved.
Using those lemmas, we can show that the
above Assumption 1 contradicts the Premise.
Similarly, at Step 3, it is proved that the Assumption
2 contradicts the Premise, using two lemmas:
Lemma 3-1 and Lemma 3-2.
(A) Lemmas in Step1
Lemma 1-1:
Let
be the event that the structural change
occurs once during the period of observation in
continuing
n times. Let be the
conditional probability that the
occurs under
the condition that failing occurs in continuing
n
times. Then,
is an increase function
for
n.
cn
E
)|(
ncn
SEP
cn
E
)|(
ncn
SEP
Lemma 1-2:
The conditional probability
)|(
1 nn
SSP
+
is a
decrease function for
n.
Those Lemmas are strictly proved subsequently
in the Appendix.
(B) Lemmas in Step2
Lemma 2-1:
If
'" NN
<
, then
),(),( NNECNNEC
′′′′
<
′
′
′
.
NEW METHOD FOR STRUCTURAL CHANGE DETECTION OF TIME SERIES AS AN OPTIMAL STOPPING
PROBLEM
27

Lemma 2-2:
If
, then, for m ( ),
'" NN <
Nm
′′
≤<0
),(),( NmNECNmNEC
′
′
−
′′
<
′
−
′′
By putting
Nm
′
′
=
in the Lemma 2-2, we
have
in case of
),0(),0( NECNEC
′′
<
′
'" NN
<
.
This inequality contradicts the Assumption 1: There
exists a number
such that and
.
"N '" NN <
)',0()",0( NECNEC <
(C) Lemmas in Step3
Lemma 3-1:
If
, then
"' NN < )','()",'( NNECNNEC ≥
where the equality holds only if
and
1'" += NN
)|()(
'1' NN
SSPaAa
+
+= ・
Lemma 3-2:
If
, then, for ( ),
"' NN <
m
'0 Nm ≤<
),(),( NmNECNmNEC
′
−
′
≥
′′
−
′
,
where the equality holds only if
and
1'" += NN
)|()(
'1' NN
SSPaAa
+
+= ・
.
By putting
in the Lemma 3-2, we have
in case of
'Nm =
)',0()",0( NECNEC ≥
NN
′
′
<
′
.
This contradicts the Assumption 2: There exists a
number
such that
N
′′
"' NN
<
and
.
),0(),0( NECNEC
′′
>
′
After all,
),0(),0( NECNEC
′′
≤
′
(
'" NN
<
or
), where the equality holds only if
and
NN
′′
<
′
1'" += NN
)|()(
'' NN
SSPaAa
1+
+= ・
.
It means that
minimizes . And, when
N
′
),0( NEC
)|()(
'1' NN
SSPaAa
+
+= ・
, also minimizes
, i.e.,
1'+N
),0( NEC
)1',0(),0( +
=
′
NECNEC
.
This completes the proof of the aforementioned
Theorem.
3 EXPERIMENTATION
3.1 Feature of Evaluation Function
We have experimented the proposed method, and
evaluated the feature of the evaluation function,
using the probability of the structural change
occurrence λ and each constant of the Equation (4),
i.e.
A and a, as parameters.
First, by numerical computing, we show the
decreasing situation of the probability
)|(
1−nn
SSP
for
n in Figure 5. In this case, the probability
approaches to 0.05 (5 %) by letting
n become
greater. It meets to the aforementioned Lemma 1-2.
0
0.2
0.4
0.6
0.8
1
12345678910
●:
λ
=0.0001
▲:
λ
=0.001
○:
λ
=0.01
n
)|(
1−nn
SSP
Figure 5: The probability
)|(
1−nn
SSP
for three kinds of
λ (occurrence probability of structural change) in the case
of
Rc=0.95
That is, we have examined the relation between
the ratio of
aAa /)(
+
and the optimum number of
times n (that is the same as aforementioned
N), by
varying the probability λ .
Experimental condition:
(i) Structural change probability λ:(three types)
0.1, 0.05, and 0.01.
(ii)
aAa /)(
+
:1.5~10.0.
(iii)Tolerance of prediction: 2σ of the distribution on
error ε.
(iv)Unfitting probability when the structure is
unchanged:
R=0.1.
(v)Unfitting probability when the structure has
changed:
Rc=0.9.
Result:
The result is shown in Figure 6, where horizontal
axis is
aAa /)(
+
and vertical axis is n. We can see
that the tendency meets our intuition, as follows.
(i) The optimum number of times
n tends to be
larger when the action cost A after the CPD is
bigger than the unfitting cost
. That is, the n
grows in the case of A > a, because the action
cost A after the change detection becomes
dominant over the loss cost
by prediction
error, and the
n decreases in the case of A < a
for the reverse reason.
a
a
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
28
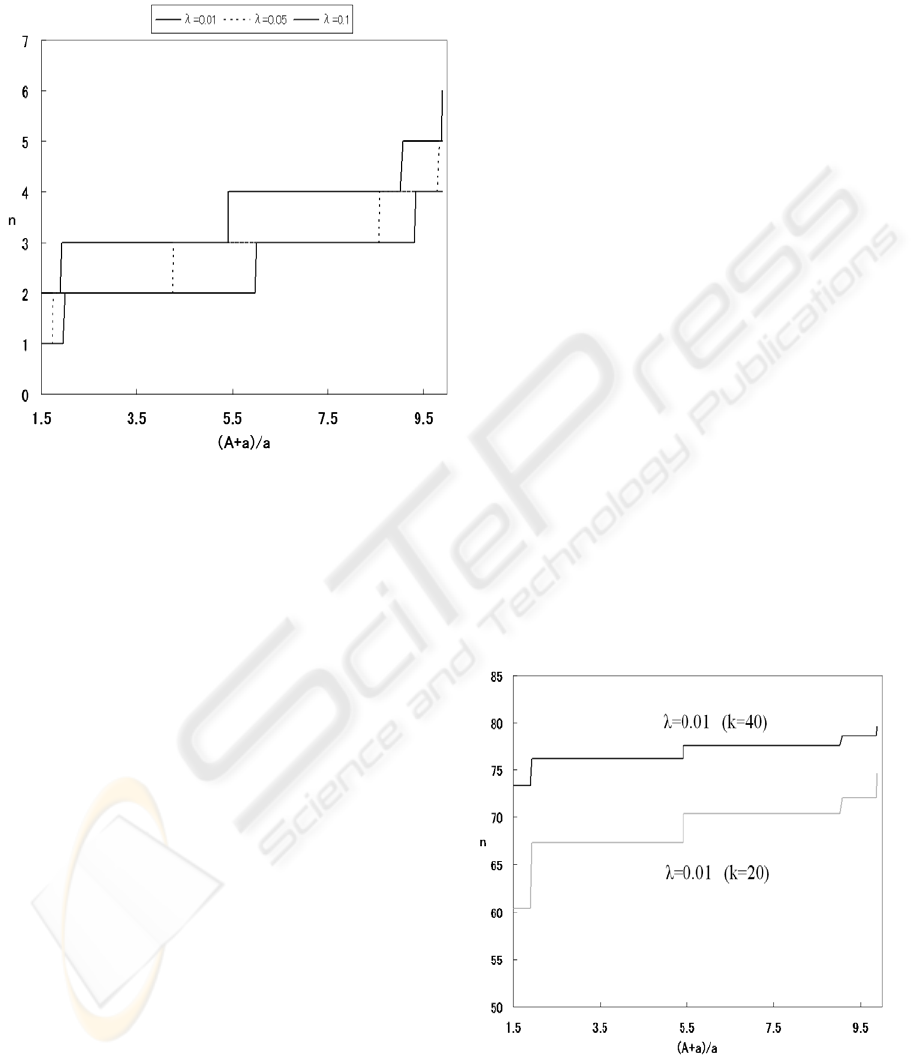
(ii) The n for the CPD increases when the
probability λ of the structural change occurrence
becomes smaller.
Figure 6: Relation between the ratio and the
optimum number of times
n
aAa /)( +
3.2 Application to Time Series Data
Since the tolerant error in the proposed method is
decided based on the residual sample distribution
when the prediction expression is estimated, the
accuracy of CPD depends on the accuracy of
prediction (or the prediction model). We examine the
fact using the time series data shown in Figure 1.
Outline of experimentation:
(i)Generate the time series data (Figure 1) based on
the Equation (1) as aforementioned in the Section
2.1, by making normal random numbers of
average 0 and variance 1.0 for ε, and by setting
β
1
=0.2, β0=1 for the time t=1,2,…,70, and β
1
=0.8,
β0=-41 for the time after t=71.
(ii)Make prediction expression, using a sequence of
data at the time t=1,…,k from the above generated
time series.
(iii)Decide the tolerant error interval.
(iv)Based on the proposed method, measure the
number of times when the observed data goes out
from the tolerance zone (or tolerant error interval)
for observation data after the time at k+1, and
detect the structural change point.
(v)Perform the above things repeatedly by M times,
and calculate the average of the structural change
point.
Experimental condition:
(i)Tolerant error interval: ± 2σ of the distribution on
error ε.
(ii)The number of data for the decision of prediction
expression: k=20, 40 (2 types).
(iii)Parameter value of the evaluation function:
λ =0.01, and
aAa /)(
+
is changed in a range of
1.5~10.0.
(iv)Repeating times: M=100.
Result:
The result is illustrated in Figure 7, where horizontal
axis shows
aAa /)(
+
and vertical axis shows the
detected change point n that is the average of 100
times computation.
Although the detection of the change point depends
on the value of
aAa /)(
+
, it is expected that the
change point will be detected around the time at
t=70, because the structure of the time series is
changed at t=70. We have verified that the result
meets our intuition very well as follows.
(A) In case of k=20, because the number of the data
for the prediction expression is less than the
case of k=40, the prediction accuracy is
considered to be so much worse. Therefore, the
unfitting frequency increases and the change
point tends to be detected early.
(B) In case of k=40, the change is detected within
the time at t=70~80. We consider that the
proposed method has appropriately detected the
change point.
Figure 7: Detected change point n for the time series in
Figure 1
NEW METHOD FOR STRUCTURAL CHANGE DETECTION OF TIME SERIES AS AN OPTIMAL STOPPING
PROBLEM
29

4 CONCLUSION
We have proposed a sequential processing method
for structural change detection of time series data,
which we formulated as an optimal stopping
problem with a cost evaluation function. We have
presented the algorithm for the optimum solution,
and have shown the correctness by proving a
theorem. The proposed method is effective in the
sense as follows.
1. Differently from the Chow test, it does not need to
set the change point in a priori.
2. Unlike the Bays’ method, it does not need to give
the generation distribution of time series data.
3. It can quickly detect the structural change point by
the sequential processing.
4. It minimizes the evaluation function that sums up
the loss involved with prediction error and action
cost to be taken after the change detection.
5. It can be applied to any prediction model.
Moreover, we have shown some numerical
experimentation results, where the resultant
situations by obtaining optimum solutions well meet
our intuition and the change point of artificially
generated time series data.
APPENDIX: PROOF OF LEMMA IN
THE STEP 1
Lemma 1-1.
The conditional probability
is an
increase function for
n.
)|(
ncn
SEP
Proof. Based on the model (see Figure 2-4), the
event
is given in (8).
cn
E
(
)
U
1
0
−
=
−
∩=
n
i
in
c
i
cn
EEE
(8)
where
E is the event that there is no structural
change,
is the event that the structural change
occurred, and
is defined as .
c
E
n
E
I
n
i
in
EE
1=
=
The probability of the event
defined in (8) is
given as follows.
cn
E
(
)
(
)
in
c
i
n
i
n
i
in
c
i
cn
EEPEEPEP
−
−
−
−
=
−
∩=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∩=
∑
1
0
1
0
)(
U
λλ−=
∑
−
=
1
0
)1(
n
i
i
(9)
Then the joint event between
and , and
the probability are given by (10) and (11),
respectively.
cn
E
n
S
(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∩∩=∩
−
=
−
U
1
0
n
i
in
c
i
ncnn
EESES
)
(10)
()
in
c
i
n
i
i
cnn
RRESP
−
−
=
λλ−=∩
∑
1
0
)1(
(11)
Therefore, using (9) and (11), we have
)(
)(
)|(
cn
cnn
cnn
EP
ESP
ESP
∩
=
∑
∑
−
=
−
=
−
λλ−
λλ−
=
1
0
1
0
)1(
)1(
n
i
i
n
i
in
c
ii
RR
(12)
According to the Bayes’ theorem, the posterior
probability
is given by the following
(13).
)|(
ncn
SEP
)()(
)(
)|(
n
ncnn
cnn
ncn
ESPESP
ESP
SEP
∩+∩
∩
=
∑
∑
−
=
−
−
=
−
λ−+λλ−
λλ−
=
1
0
1
0
)1()1(
)1(
n
i
nnin
c
ii
n
i
in
c
ii
RRR
RR
∑
−
=
−
−
−
+
=
1
0
λλ)1(
λ)1(
1
1
n
i
in
c
ii
nn
RR
R
)(1
1
nD+
=
(13)
where
∑
−
=
−
−
−
=
1
0
λλ)1(
λ)1(
)(
n
i
in
c
ii
nn
RR
R
nD
.
The D(n) is also expressed as the following (14).
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
30

∑
∑
−
=
−
=
λ
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
λ−λ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
λ−
=
1
0
1
0
X
X
)1(
)1(
)(
n
i
i
n
n
i
i
c
i
n
c
n
R
R
R
R
nD
⎟
⎠
⎞
⎜
⎝
⎛
⋅⋅⋅++λ
=
−
XX
1
X
1
1
1
1
+
nn
(14)
where
c
R
R
)(1X λ-=
.
Since
, , and ,
then 0 < X < 1. So, the D(n) becomes a monotonous
decrease for n. Therefore, the probability
of (13) is a monotonous increase
function for n. Lemma 1-1 is proved.
10 <λ≤ 110 ≤λ−<
RR
c
>
)|(
ncn
SEP
Remark: Lemma 1-1 indicates that, if the
number of times of the unfitting n increases, the
probability that the structural change has occurred
increases. This meets our intuition clearly.
Lemma 1-2.
The conditional probability
)|(
1 nn
SSP
+
is a
decrease function for n.
Proof. Based on the model in Fig. 3, we have
))|(1)(1()|(
1 ncnnn
SEPRSSP −−=
+
)|()1(
ncnc
SEPR−+
(15)
The first term in the RHS of (15) shows the
probability that the fitting occurs for the (n+1)-th
time observed data when the structure is unchanged.
The second term shows the probability that the
fitting occurs for the (n+1)-th time observed data
when the structure changed.
From (15), we have
))(|(1)|(
1 cncnnn
RRSEPRSSP −+−=
+
(16)
By Lemma 1-2,
is an increase
function, and
, therefore,
)|(
ncn
SEP
c
RR <
)|(
1 nn
SSP
+
is a
decrease function for n. Lemma 1-2 is proved.
Remark: Lemma 1-2 indicates that, if the
number of times of continuous unfitting increases,
the probability of the fitting for the next observed
data after those continuous unfitting decreases. This
is intuitively clear, because, by Lemma 1-1, the
probability of the structural change increases if the
number of times of the continuous unfitting
increases.
REFERENCES
R.Jana and S.Dey, 2000. Change detection in Teletraffic
Models. IEEE Trans. Signal Processing, vol.48, No.3,
pp.846-853, March 2000.
R.M.Gagliardi and I.S.Reed, 1965. On the Sequential
detection of Emerging Targets. IEEE Trans.
Information Theory, vol.6, pp.260-263, April 1965.
R.J.Di Francesco, 1990. Real-Time Speech segmentation
Using Pitch and Convexity Jump Models. IEEE Trans.
Acoustics, Speech, Signal Processing, vol.38, pp.741-
748, May 1990.
A.S.Willsky, 1996. A survey of design methods for failure
detection in dynamic systems. Automatica, Vol.12. pp.
601-611, Sept. 1996.
D.Kauame and J.P.remenieras et al., 1996. Effect of The
Compensation In Abrupt Model Change Detection
Problem.
Proc. of IEEE Digital Signal Processing
Workshop, pp.311-314, Sept. 1996.
Chow,G.C., 1960. Tests of Equality Between Sets of
Coefficients in Two Linear Regressions.
Econometrica, Vol.28, No.3, pp.591-605, July 1960.
S.MacDougall, A.K.Nandi and R.Chapman, 1998.
Multisolution and hybrid Bayesian algorithms for
automatic detection of change points.
Proc. of IEEE
Visual Image Signal Processing, vol.145, No.4,
pp.280-286, August 1998.
V.V.Veeravalli and A.G.Tartakovsky, 2002. Asymptotics
of quickest change detection procedures under a
Bayesian criterion.
ITW2002, pp.100-103, Bangalore,
India, Oct. 2002.
E.S.Page, 1954. Continuous inspection schemes.
Biometrika, Vol. 41, pp.100-115, 1954.
C.Han,P.k.Willet and D.A.Abraham, 1999. Some methods
to evaluate the performance of Page's test as used to
detect transient signals. IEEE Trans. Signal
processing, vol.47, No.8, pp.2112-2127, August 1999.
S.D.Blostein, 1991. Quickest detection of a time-varying
change in distribution. IEEE Trans. Information
Theory, vol.37, No.4, pp.1116-1122, July 1991.
Y.Liu, S.D.Blostein, 1994. Quickest detection of an abrupt
change in a random sequence with finite change-time.
IEEE Trans. Information Theory, vol.40, No.6,
pp.1985-1993, Nov. 1994.
M.Basseville and I.V.Nikiforov, 1993. Detection and
Application, Prentice Hall, Inc., April 1993.
M.Basseville, 1988.Detecting Changes in signals and
systems– A survey. Automatica,Vol.24, pp.309-
326, 1988.
N.R.Draper, H.Smith, 1996. Applied Regression Analysis,
John Wiley & Sons Inc, 1966.
NEW METHOD FOR STRUCTURAL CHANGE DETECTION OF TIME SERIES AS AN OPTIMAL STOPPING
PROBLEM
31
