Neural Networks and Rainfall-Runoff Model, its

Calibration and Validation

U.Ghani

A.R. Ghumman

, M.A.Shamim

1, 2, 3

Civil Engineering Department - University of Engineering & Technology, Taxila –

Pakistan

Keywords. Rainfall-runoff, Watershed, Neural networks.

Abstract. In this study a rainfall-runoff model was developed with the help of

neural networks. Input to the model is precipitation and potential

evapotranspiration (both on monthly basis). Output from the model is the

simulated runoff at the watershed outlet. The model was calibrated and tested

for Brandu river catchment of Pakistan.The data was collected from

Meteorological Department Pakistan. Statistical results showed that the model

preformed well. The correlation co-efficient between the simulated and

measured data was found to be 87.5%.

1 Introduction

Structural and non-structural designs of some hydraulic structures, reservoir operation

and water resources development projects need river flow hydrographs. For such

hydrographs simulation of watershed response to hydrologic inputs is required.

Various researchers have developed monthly water balance models, Pitman

(1973), Mather (1981), Alley (1984), Vandewiele et al (1992), Xu & Vandewiele

(1995), Huges (1995) and Vandewiele et al (1998). These models are rarely static.

They undergo frequent modifications by their developer or by a subsequent user.

Stefan et al (1999), Liden (2000), Madsen (2000) and Shan (2000) studied the

performance of a conceptual rainfall runoff models. The complexity of models varies

according to data availability, type of hydrologic quantity to be modeled, scale of

operation, required accuracy, computer facilities and economic considerations.

Generally, there is no universal model, which

could be applied successfully to all

hydrologic basins as the natural processes are highly random and models are data

dependent.

Neural network techniques have provided solution to this problem up to

some extent. Although these models do not provide understanding of the watershed

response but still the model results have many important

applications. Researchers in

the field of Hydrology have started modeling using neural networks Oscar R.Dolling

& Eduardo A.Varas (2002); Tawatchai Tingsanchali (2003) ; Yi-Ming, Kuo Chen –

Wuing Liu & Kao-Hung Lin(2004).

Ghani U., Ghumman A. and Shamim M. (2004).

Neural Networks and Rainfall-Runoff Model, its Calibration and Validation.

In Proceedings of the First International Workshop on Artiﬁcial Neural Networks: Data Preparation Techniques and Application Development, pages

60-66

DOI: 10.5220/0001150000600066

 SciTePress

The present study is an effort to address the problem of simulating runoff

from a watershed with the help of neural networks. A mathematical model was

developed and run on a P-IV computer. The model was tested using measured data of

watershed. Statistical tests were performed to examine the performance of the model.

2 Description of the study areas

The watersheds selected for calibration and validation of the model was based on two

criteria: (a) there is no snow melt contribution to total runoff which cannot be

simulated by the model, (b) a continuous record of observed runoff is available, which

is used for calibration and validation of the model. Brandu River Watershed, was

selected for study.

Brandu River Watershed is located in Swat district of NWFP, Pakistan.

The elevation ranges between 732 m to 2134 m above mean sea level. The drainage

area of Brandu River is 598 km

. The climate of the study area is sub-tropical sub-

humid continental, and has a record of 1025.72 mm mean annual precipitation. The

soils and landforms are loess plains, piedmont plains, river alluvium and

miscellaneous areas (rough broken land, gulled land, rough mountainous land, stony

land). The land in the valley of the study area is cultivated and has good vegetation

cover due to the availability of very shallow groundwater, whereas the hill slopes of

the watershed are sparsely vegetated. The main season of rainfall in the study area is

the monsoon from July to September, which is the major contribution of flow in the

river. The other seasons of the year have low rainfall rate, but occasionally high

storms of single event do occur. Therefore high flows in the river are occurring during

summer season and low flows during the other seasons. Baseflow and groundwater

are contributing to the Brandu River flows. This is indicated from some high flows

against low rainfall rate from the data of the watershed and reported studies of the

area (Soil Survey of Pakistan 1975). According to this the groundwater is available at

shallow depths.

3 Neural networking Models

As mentioned in our first paper the Artificial Neural networks are increasingly used in

predicting and forecasting water resource variables (Nash, J.E. and Sutcliffe (1970),

French et, M.N. (1992), Zhu, M.L. and Fujita, M. (1994), Dawson C. W. & Wilby R.

L.(2001), Yi-Ming Kuo (2003)). Hydrologic models can be divided into three broad

categories, namely: Physical distributed models, lumped conceptual models and black

box models.

Physical based distributed models require excessive field data whereas in

case of lumped conceptual models, large number of parameters and subsequent

difficulty in calibration is involved. Both of these models are used where detailed

understanding of the hydraulic phenomenon is necessary. Black box models do not

contribute much in enhancing the understanding of hydrological and hydraulic

phenomena; nevertheless in operational hydrology and hydraulic Engineering their

usefulness is of utmost importance. Neural Networking models can be considered as

black box models. These are easy to use and have comparatively less data

requirements. This is the reason why they are becoming popular and are recently

being used in the field of Water Resources Engineering also. EasyNN model based on

Neural Networking was used to simulate runoff from a catchment area.

4 Training

This has also been described in our first paper submitted for this conference. The

training process estimates the Artificial Neural Networks (ANN) weights and is

similar to the calibration of a mathematical model. The ANNs are trained with a

training set of input and known out put data. The weights are initialized either with a

set of random values, or based upon some previous experience. These weights keep

on changing till the goal is achieved. The goal of learning is to determine a set of

weights that will minimize the error function.

5 Training and Validation

The input data of the model were taken as the observed monthly rainfall and

evaporation for Brandu River Catchment. The monthly measured runoff data for the

same catchment were used as the target in the EasyNN model calibration and

validation. The aim was to forecast monthly runoff from the catchment if rainfall and

evaporation is known. By considering the data from1971-1980 the training was

carried out. This was done in twelve steps taking ten years data for a specific month

for each step. For validation the measured data of rainfall, evaporation and runoff for

1981 to 1989 was used.

6 Calibration and Validation tests

Ten years (1971 to 1980) rainfall runoff and evaporation data was used for model

calibration. The model was tested using other set of data from 1981 to 1989 for the same

catchment. Statistical analysis was performed using four statistical parameters,

mathematically given as (Mutreja 1986):

[]

)(

∑

−

ojo

ojc

(1)

= (C

)

(2)

()

[]

jcjo

∑

−

)(

(3)

Where: C

is coefficient of correlation, C

is coefficient of determination and S

standard error of estimates.

is mean observed runoff and is equal to

joo R

R )(

∑= , where N is the length of record.

7 Results and Discussion

Figures 1 presents a comparison between observed and simulated run off .The graphs

shows good similarity between observed and simulated runoff. The goodness of fit of

these graphs is measured by three statistical parameters, C

, C

& S

which were

described in previous section. . The results of these tests are given in table 1.

The model developed in this study performed well. The statistical measures

in case of calibration have better results than that in case of

verification. It usually

happens that the error variance during validation is in excess of the error variance

during fitting period.

Table 1 shows that model developed in this study performed better than the

Pitman model although the present model is a black box model.

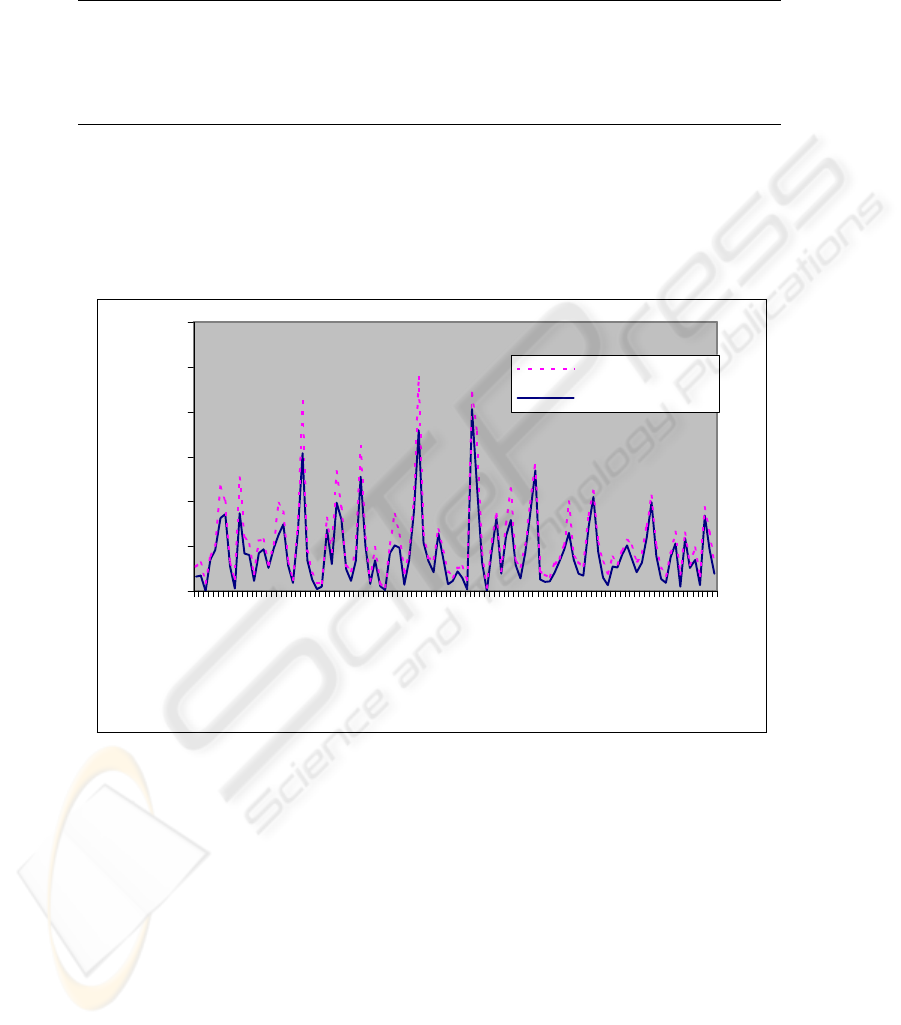
Table 1. Results of statistical tests (Validation of model).

100

200

300

400

500

600

106

months

runoff (mm)

Sim runoff(mm)

Obs runoff(mm)

8 Conclusions

A model has been developed which is robust and works as black box model. The

model has a good performance over a wide range of climatic conditions. Working

with measured data of rainfall and runoff requires great efforts for calibrating model

parameters due to the influence of the quality of observed data. Because the

parameters act as “catch all parameters”, black box model based on neural networks

can be adopted for such conditions, thus reducing complexity of calibration and the

problem of non-availability of data required for the analysis.

Watershed

Statistical

Parameter

Developed

Model

Pitman Model

(from M.S.Abulohom.2001)

0.875 0.81

Brandu

River

0.766 0.67

8.9 11.96

References

1. Abulohom, M. S. 1997. Calibration of a mathematical model for generating monthly River

Flows from meteorological data for a selected catchment. M.Sc thesis, CEWRE, UET,

Lahore, Pakistan.

2. Abulohom, M. S&.S. M .S. Shah, A.R.Ghumman 2001. Development of a Rainfall-Runoff

Model, its Calibration and Validation. Journal of Water Resources Management. Vol. 15

No.3. 2001

3. Alley, W.M. 1984. On the treatment of evapotranspiration, soil moisture accounting an

aquifer recharge in monthly water balance models. Water resources Research Vol. 20(8):

1137-1149.

4. C,-Y.XU & Vandewiele, G.L. 1995. Sensitivity of monthly rainfall-runoff models to input

errors and data length. Hydrological Sciences Journal. Vol. 39(2): 157-176.

5. Dawson, C. W. and Wilby, R. L.2001. “ Hydrological Modeling using Artificial Neural

Networks”, Progress in Physical Geography, Arnold.

6. French, M.N.; Krajewski, W.F. and Cuykendall, R.R.1992. “Rainfall forecasting in space

and time using a neural network”, Journal of Hydrology, Vol. 137, 1-31.

7. Hughes, D.A. 1995. Monthly rainfall-runoff models applied to arid and semiarid catchments

for water resources estimation purposes. Hydrological Sciences Journal. Vol. 40(6): 751-

769.

8. Liden, R. & Harlin. J. 2000. Analysis of conceptual rainfall-runoff modeling performance in

different climates. Journal of Hydrology Vol. 238: 231-247.

9. Madsen, H. 2000. Automatic calibration of a conceptual rainfall-runoff model using

multiple objectives. Journal of Hydrology Vol. 235: 276-288.

10.Mather, J.R 1981 Using computed streamflow in watershed analysis. Water resources

bulletin vole 17(3): 474-482

11.Mutreja, K.M. 1986. Hydrologic synthesis and simulation. Applied Hydrology. Pp. 613-668.

12.Nash, J.E. and Sutcliffe, J.V.1970, “River flow forecasting through conceptual models, part

I, A discussion of Principles”, Journal of Hydrology, 10(3), pp. 282-290.

13.Oscar R.Dolling and Eduardo A. Varas. 2002. Artificial Neural Networks For

Streamflow.Prediction. Journal of Hydraulic Research Vol 40,2002,No.5.

14.Pitman, W.V. 1973. A mathematical model for generating monthly River Flows from

meteorological data in South Africa. A Ph.D. thesis, Hydrological Research Unit, University

of Witwatersrand, South Africa.

15.Soil survey of Pakistan department, 1975. Reconnaissance soil survey. Soil survey of

Pakistan.

16.Stefan Uhlenbrook, Jan Scibert, Christian Leibundgut and Allan Rodhe. 1999. Prediction

uncertainty of conceptual rainfall-runoff models caused by problems in identifying model

parameters and structure. Hydrological Sciences Journal Vol 44(5): 779-797.

17.Tawatchai Tangsanchali. Forecasting Model of Chao Phraya River Flood Levels at

Bangkok.

18.Vandewiele, G.L, and Atlabachew, E. 1995. Monthly water balance of ungauged

catchments obtained by geographical regionalization. Journal of Hydrology, Vol. 170: 277-

291.

19.Vandewiele, G.L, Chong-Yu Xu, and Ni-Lar-Win. 1992. Methodology and comparative

study of monthly water balance models in Belgium, China and Burma. Journal of

Hydrology, Vol. 134: 315-347.

20.Vandewiele, G.L. and Ni-Lar-Win 1998. Monthly water balance models for 55 basins in 10

Countries. Hydrological Sciences Journal. Vol. 43(5): 687-699.

21.Victor Miguel Ponce. 1989. Ctachment Routing. Engineering Hydrology. Pp.306-331.

22.Yi-Ming Kuo, Chen-Wuing Liu, Kao-Hung Lin. Evaluation of the ability of an Artificial

Neural network model to assess the variation of Groundwater quality in an area of blackfoot

disease in Taiwan. Water Research 38(2004) 148-158.

23.Yu Pao-Shan & Chang-Yan Tao. 2000. FUZZY multi objective function for rainfall-runoff

model calibration. Journal of Hydrology Vol 238: 1-14.

24.Zhu, M.L. and Fujita, M.1994, “Comparison between fuzzy reasoning and neural networks

methods to forecast runoff discharge”, Journal of Hydro science and Hydraulic Engineering,

Vol. 12, No. 2, 131-141.