
Global Path Planning Based on Neural Network and
Genetic Algorithm in A Static Environment
Huahua Chen, Xin Du, Weikang Gu
Department of Information Science and Electronics Engineering, Zhejiang University,
310027 Hangzhou, China
Abstract. Mobile robot global path planning in a static environment is an im-
portant
problem all along. The paper proposes a method of global path planning
based on neural network and genetic algorithm. The neural network model of
environmental information in the workspace for a robot is constructed. Using
this model, the relationship between a collision avoidance path and the output
of the model is established. Then the two-dimensional coding for the via-points
of path is converted to one-dimensional one and the fitness of the collision
avoidance path and that of the shortest distance are fused to a fitness function.
The simulation results show that the proposed method is correct and effective.
1 Introduction
The path planning problem of a mobile robot can be stated as: given a start location, a
goal location, and a set of obstacles distributed in a workspace: find a safe and effi-
cient path for the robot. Thus the robot can go from the start location to the goal loca-
tion without colliding with any obstacles along the path. In addition to the fundamen-
tal problem, we might also seek to optimize the plan in some way, say to minimize
time required or distance traveled[1][2][3][4].
The popular methods are the visibility graph algorithm
and the artificial potential
field algorithm. However, the former is lack of flexibility and the latter is prone to
suffer from difficulties with local minima[5][6][7].Genetic algorithm is multi-search
algorithm based on the principles of natural genetics and natural selection[8].The
major advantages of genetic algorithm are that they provide a robust search in com-
plex spaces and are usually computationally less expensive when compared to other
search algorithms. Genetic algorithm searches from a population of points and is less
likely to be trapped in a local optimum. Many results exist in the literature which
show the better application of genetic algorithm in robot path planning[9][10][11].
Autonomous navigation, in general, assum
es an environment with known and un-
known obstacles. It includes global path planning algorithms to plan the robot’s path
among the known obstacles, as well as local path planning for real time obstacle-
avoidance[3][4].There is a very important problem about how to plan an optimal path
in a static environment which is called static path planning and has a wide range of
applications[12].In this paper, a new technique based on the concepts of neural net-
work and genetic algorithm is proposed.
Chen H., Du X. and Gu W. (2004).
Global Path Planning Based on Neural Network and Genetic Algorithm in A Static Environment.
In Proceedings of the First International Workshop on Artificial Neural Networks: Data Preparation Techniques and Application Development, pages
32-40
DOI: 10.5220/0001150700320040
Copyright
c
SciTePress
In Section 2, we construct a neural network model of environmental information in
the workspace for a robot and establish the relationship between a collision avoidance
path and the output of the model using this model. Section 3 converts the two-
dimensional via-points of path to one-dimensional one and fuses the fitness of both
the collision avoidance path and the shortest distance to a simple fitness function.
Section 4 presents the computer simulation about a robot path planning problem.
Section 5 is the conclusion.
2 Environment Modeling by Neural Network
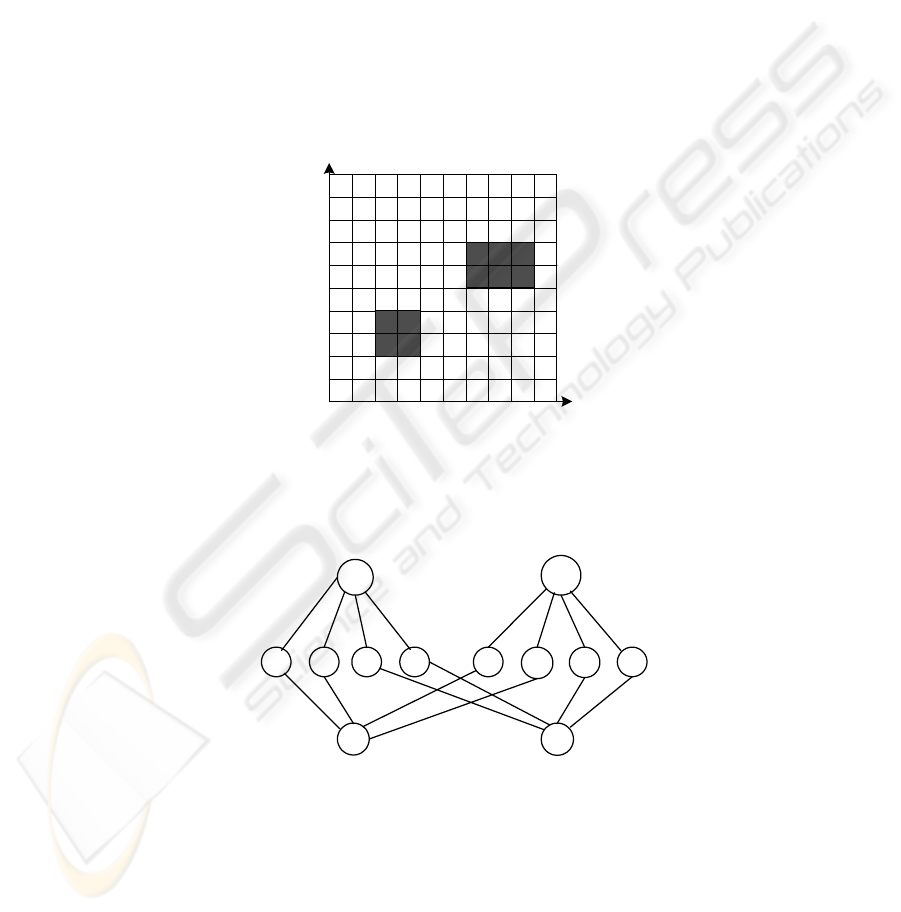
Firstly, we suppose the workspace for the robot coincides with conditions below:
(1)the robot moves in a limited two-dimensional space.
Y
X
O
Fig. 1. The workspace for a robot
-3.5
-2
-2
4
4
-6
9
-5
7
X
i
Yi
1
i
C
2
i
C
I
T
11 1 1
11 11
M
m
O
f
M
m
I
1
1
1
1
-1
-1
-1
-1
x
m
w
ym
w
-3.5
f
Fig. 2. The neural network for the environment
(2)the robot can be considered as a particle if the boundary of each obstacle is extend
the half size of the robot’s maximal dimension in length or width direction.
33

(3)the obstacles in the workspace can be described as convex polygons.
Without loss of generality, suppose the workspace for a robot is shown in Fig. 1,
and the shadowed parts represent the obstacles. According to [13], the environment
can be described by the neural network shown in Fig. 2 which can be represented by
equations (1).
1
1
()
()
iI
M
IMmT
m
Mm Mm
Mm xm i ym i Mm
CfT
TO
OfI
IwXwY
θ
θ
=
⎫
=
⎪
⎪
=+
⎪
⎬
⎪
=
⎪
=++
⎪
⎭
∑
.
(1)
where
C
i
1
,C
i
2
: the outputs of the nodes of the top layer
I
T
: the input of the nodes of the top layer
T
θ
: the threshold of the nodes of the top layer
M
m
O
: the output of the mth node of the medium layer
M
m
I
: the input of the mth node of the medium layer
M
m
θ
: the threshold of the mth node
xm ym
ww,
: the weights from the input layer to the medium layer
() 1(1 )
xT
fx e
−
=+ : the excited function
(X
i
,Y
i
): a random point in the workspace
The output of the neural network model of each point in the workspace is 0 or 1.
When C
i
k
=1 (k=1,2) it implies that (X
i
,Y
i
) is in the kth obstacle region otherwise it
doesn’t.
If the radius of the robot could be ignored, the robot can be regarded as a particle.
When the robot arrives (X
i
,Y
i
) whose output of the neural network model is C
i
k
=1
(k=1,2), it collides with the kth obstacle in the workspace. On the contrary, it doesn’t.
Thus the collision avoidance path can be described as the path in which each (X
i
,Y
i
)
whose output of the neural network model is C
i
k
=0 (k=1,2).
In Fig. 1, the workspace is made of two obstacles and the neural network model is
simple. If more than two obstacles in the workspace, the model will be complex cor-
respondingly. It is described in Fig. 3.
34
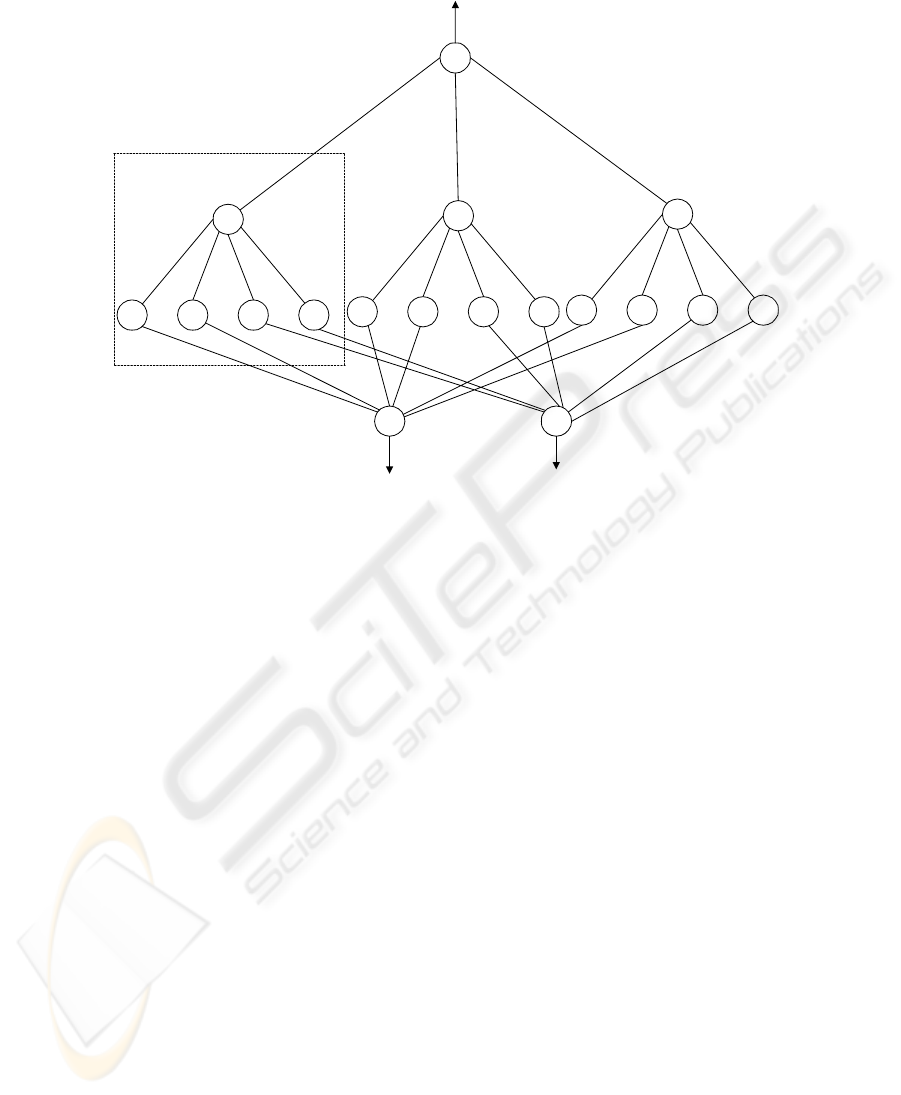
...
Xi Yi
1
i
C
2
i
C
n
i
C
1
n
k
i
k
C
=
∑
1
st obst acl e
2
nd obst acl e
n
th obstacle
Fig. 3. The neural network for the multi-obstacle environment
3 Path Planning Based on Genetic Algorithm
3.1 Path Coding
In genetic searching algorithm, the coding technique is important in that the length of
binary strings, from the parameter sets made of the via-points of a path , as well as the
size of search space determines the computational time for a given fitness function.
We devise a simple coding technique to shorten the length of the binary string by
projecting the two-dimensional data to one- dimensional ones as shown in Fig. 4. The
aim of the algorithm is to determine the node points (x
i
,y
i
) (i=1,2,…,n) that consti-
tutes the start to the goal position. In order to reduce the length of the string, we
convert the workspace XOY, in which each node point of path is two-dimensional, to
a new coordinate space xo’y, whose x axis is the line determined by the start and the
goal position, in which each node point of path is one-dimensional. Then the set of
the node points x
i
is located in the equal distance along the x axis. Therefore, y
i
be-
comes the search space for each via-point of the robot path and the via-point candi-
dates are specified by the one-dimensional data.
The coding is done in float type and its structure is shown in Fig. 5.
35

Y
XO
st ar t
goal
y
x
1
x
i
x
n
x
1
y
i
y
n
y
O
'
Fig. 4. Projecting of search space. XOY is workspace and xo’y is the converted coordinate
space
y
1
y
2
y
3
y
n
Fig. 5. The coding structure
3.2 Fitness Function
The fitness function is an important factor to the convergence and the stability of
genetic algorithm. The path planning should be satisfied with collision avoidance and
the shortest distance. The summation of each evaluation function weight is a typical
method to construct the fitness function[11][14], but it is prone to instable and its
weight coefficients are difficult to tune and determine for they are variable as the path
and the obstacles change. So when we construct the fitness function, the number of
evaluation functions is as small as possible. On the other hand, the two evaluation
functions, collision avoidance and the shortest distance, must be fused in a fitness
function.
Collision avoidance is essential to path planning and make the mobile robot travel
in the workspace safely. Collision avoidance can be depicted as:
(1)each via-point y
i
is not in the any obstacle, whose fitness value is fit11;
(2)each section y
i
y
i+1
does not intersect the any obstacle, whose fitness value is
fit12.
Suppose the workspace for the robot is shown in Fig. 4, the via-point y
i
can not be
in the obstacle regions. Combined with the output of the neural network model, the
fitness function of collision avoidance fit1 can be described as the equation (2).
11112
f
it fit fit
=
×
,
(2)
36

10(
11
0
k
i
if C k
fit
others
⎧
==
=
⎨
⎩
1,2)
∑
,
1
0
12
1
ii
y y obstacle
fit
others
+
⎧
=
⎨
⎩
I
.
where i is the ith point in the path. The equation (2) implies that the path is collision
avoidance if the fitness value of the each via-point in the path is 1 otherwise is 0.
In addition to collision avoidance, the path can be optimized for minimum distance
and its fitness function fit2 can be described as the equation (3).
1
22
11
0
2( )(
n
ii ii
i
)
f
it x x y y
−
++
=
=−+−
∑
.
(3)
Thus the final fitness function is constructed as the equation (4). This not only
makes computation simple but also overcomes the disadvantage of the instability
from the summation of evaluation function weights.
12
f
it fit fit
=
×
.
(4)
3.3 Genetic Operations Definition
Initial population is generated by choosing the node points randomly, in the lines
through the set x
1
, x
2
,…,x
n
and perpendicular to the x axis in the workspace. The size
of the population indicates the number of the path in the workspace. The larger size
produces the more accurate path and the global optimum is likely to find, but compu-
tation time is longer correspondingly. In general, the size of the population is between
[20,100], in this paper it is 30.
Selection or reproduction: It is a process in which individual strings are copied into
the next population according to their fitness, i.e., the “better” strings survive to re-
produce and the less highly fit strings “die”. Fitness of a string is determined by the
objective function which is to be optimized. There are several different methods for
determining how effectively a given string “competes” in the reproduction process. In
this paper, Monte Carlo method is used. Besides, the individual smallest fitness value
in the next generation is replaced by the individual highest fitness value in the previ-
ous one in order to make the optimal individual undestoyed during the evolutionary
process.
Crossover: The above operation can find the optimum in the existing population
but can’t produce the individuals that are different to the previous ones. Then cross-
over can do this by swapping characters according to some probability to create new
strings so that “better “ ones can be produced. The probability determines the fre-
quency of crossover. The higher frequency gets the higher speed to the optimum, but
it is probable to converge before the optimum arises. In general, the probability is
37

between [0.4,0.9].In the proposed algorithm, one-point crossover is done and the
crossover position and the number of points are generated randomly.
Mutation: The Reproduction and the crossover can find the optimum in the exist-
ing character arrays, but sometimes fail to produce new characters that make the
problem found the best solution for premature convergence. The mutation changes
the characters in an individual string with a very small probability between
[0.001,0.4]. Mutation brings in new possibilities for improvements and takes care of
some of the lost information during crossover and reproduction. Then the fitness
values of the new population’s strings are evaluated. To mutate an individual, zero
mean white Gaussian noise is added to y
i
.
4 Simulation Results
Fig. 6. Simulation results of the global path planning for Fig.4
To show how the algorithm proposed in this paper works, suppose that the number of
initial population is 30, the crossover probability is 0.65, the mutation probability is
0.25, and maximal offspring generation is 1000. In this case, the final answer is
showed in Fig. 6. Obstacles, start and goal position are marked as rectangles and
circles respectively.
Besides, we give two further examples under multi-obstacle environment, and the
results are showed in Fig. 7 and Fig. 8. In Fig. 7, the simple environment is made of
five obstacles and they are depicted as rectangles. In section 2, we suppose the obsta-
cles are convex polygons. In Fig. 8, the complicated environment is made of many
obstacles and they are indicated as different shape, but all of them can be imple-
mented using the model shown in Fig. 3 by properly extending the size of obstacles.
Fig. 6,7 and 8 show that the robot can go from the start to the goal position without
colliding with any obstacle in a static environment. The experiment results which
demonstrate successful usage of the proposed global path planning algorithm are
correct and effective.
38

Fig. 7. Simulation results of the global path planning for multi-obstacle simple environment
Fig. 8. Simulation results of the global path planning for multi-obstacle complicated environ-
ment
5 Conclusion
In this paper, a global path planning algorithm based on neural network and genetic
algorithm is proposed for mobile robot navigation in a static environment. Computer
simulation and experimental results are given to show the feasibility of the proposed
algorithm.
References
1. Wu, K. H., Chen, C. H., Lee, J. D.: Genetic-based Adaptive Fuzzy Controller for Robot Path
Planning. Proceedings of the Fifth IEEE International Conference on Fuzzy Systems,Vol.3.
(1996) 1687 –1692
2. Sadati, N., Taheri, J.: Genetic Algorithm in Robot Path Planning Problem in Crisp and
Fuzzified Environments. IEEE International Conference on Industrial Technology, Vol.1.
(2002) 175 –180
39

3. Ramakrishnan, R., Zein-Sabatto S.: Multiple Path Planning for A Group of Mobile Robots in
a 3D Environment Using Genetic Algorithms. Proceedings of IEEE SoutheastCon, (2001)
65 –71
4. Ramakrishnan, R., Zein-Sabatto S.: Multiple Path Planning for A Group of Mobile Robots in
a 2D Environment Using Genetic Algorithms. Proceedings of IEEE SoutheastCon, (2002)
359–363
5. Alexopoulos, C., Griffin, P. M. : Path Planning for a Mobile Robot. IEEE Transactions on
Systems, Man and Cybernetics, Vol.22. (1992) 318 –322
6. Chen, L., Liu, D. Y.: An Efficient Algorithm for Finding a Collision-Free Path Among Poly-
hedral
Obstacles. Journal of Robotics Systems, Vol.7. (1990) 129 –137
7. Borenstein, J., Koren Y.: Real-Time Obstacle Avoidance for Manipulators and Mobile Ro-
bots. IEEE Transactions on Systems, Man and Cybernetics, Vol.19. (1989) 1179 –1187
8. Goldberg, D. E.: Genetic Algorithm in Search, Optimization and Machine Learning. Assion-
Wesley Publishing Company, Inc.(1989)
9. Khoogar, A. R., Parker, J. K.: Obstacle Avoidance of Redundant Manipulators Using Ge-
netic Algorithms. Proceedings IEEE International Conference on Robotics and Automation,
Vol.1. (1991) 317 –320
10.Ram, A., Arkin, R., Boone, G.: Using Genetic Algorithms to Learn Reactive Control Pa-
rameters for Autonomous Robotic Navgation. Adaptive Behavior, Vol.2. (1994) 277 –305
11.Noboru, N., Hideo,T.: Path Planning of Agricultural Mobile Robot by Neural Network and
Genetic Algorithm. Computers and Electronics in Agriculture, Vol.18. (1997) 187 –204
12.Wang ,C., Soh, Y. C., Wang,H.: A Hierarchical Genetic Algorithm for Path Planning in A
Static Environment with Obstacles. IEEE Canadian Conference on Electrical and Computer
Engineering, Vol.7. (2002) 1652 –1657
13.Zhu, Y., Chang, J., Wang, S.: A New Path-planning Algorithm for Mobile Robot Based on
Neural Network. IEEE Region tenth Conference on Computers, Communications, Control
and Power Engineering, Vol.13. (2002) 1570 –1573
14.Woonggie, H., Seungmin, B., Taeyong, K.: Genetic Algorithm Based Path Planning and
Dynamic Obstacle Avoidance of Mobile Robots. IEEE International Conference on Compu-
tational Cybernetics and Simulation,
Vol.3. (1997) 2747 –2751
40
