STRUCTURED DOCUMENTS REPRESENTED BY

CONCEPTUAL GRAPHS

A simple formalism for presenting structured documents

Vanyo G. Peychev

Computer Science Dept., Sofia University, 5 James Baucher, 1164 Sofia,Bulgaria

Jimmy C. Dubuisson

IT Division, Voltimum, Geneva, Switzerland

Vladimir T. Dimitrov

FMI, Sofia University, 1164 Sofia, Bulgaria

Zhechka A. Toteva

EP Department, CERN, CH-1211 Geneva, Switzerland

Keywords: structured document, conceptual graphs, formal

document model, XML, DTD

Abstract: Each structured document can be represented by means of XML and an associated DTD. The goal of this

article is to present a formal model of a structured document, and to make a representation of a document

described by the model with a conceptual graph and a related DTD.

1 INTRODUCTION

A text document usually has some structure on its

own. Such a document can be divided into chapters,

pages, sentences, paragraphs, sections, volumes,

lines, verses and stanzas. A document may include a

title, a preface, a summary, an epilogue, some

quotes, references, emphasized parts, digressions or

notes. The characteristics of documents vary a lot. A

document may have an identified author, or it may

be anonymous; it may be precisely dated, or not

dated at all; it may be part of a larger work, or it may

be a standalone document. Each document is

structured differently and this structure may even

vary from part to part inside the same document.

We could consider the document processing as

obligatory part of the contemporary information

systems. This means that a structured presentation of

document is a way for improving the document

processing. A structured presentation allows the

application of well-known search methods. Another

advantage of using a structured presentation of

documents concerns the data visualization, which is

achieved by processing operations. Defined structure

is a way for programming the possibilities for

visualization, especially for equipments with limited

resources, e.g. PDA, mobile devices, etc. The lack of

a formal model for structured presentation of a

document, as well as the mentioned advantages, is

another motif for researching the possibilities for

structural presentation of documents. The goal of the

work is to present a formal model for structured

documents.

This article concerns only documents containing

tex

t information, while hypertext documents will not

be considered in this article.

1.1 Related works

Researches made over structural documents are

oriented to the modeling of documents, either from

the point of view of operations over a document or,

257

G. Peychev V., C. Dubuisson J., T. Dimitrov V. and A. Toteva Z. (2004).

STRUCTURED DOCUMENTS REPRESENTED BY CONCEPTUAL GRAPHS - A simple formalism for presenting structured documents.

In Proceedings of the First International Conference on E-Business and Telecommunication Networks, pages 257-262

DOI: 10.5220/0001383002570262

 SciTePress

from the point of view of subject area. Clarke

(Clarke, 1994) supposes that every structured

document is labeled and he defines a metric for it.

He creates a model for a text database as a string of

concatenated symbols drawn from a text alphabet

and a stoplist alphabet. The goal of his

investigations is the definition of operations over a

structured document. Query algebra is presented and

it expresses searches over structured texts.

Calvanese, De Giacomo and Lenzerini (Calvanese,

1999 and Groß-Hardt, 2002) consider structured

documents in terms of XML and DTD. Again, the

goal of their research is the definition of operations

over structured documents using description logic.

1.2 Article structure

The article consists of four parts. There is a formal

presentation of a structured document model in the

first one. The model presents a description of a

document, without taking into account the

operations over it, as the operations over different

types of documents are quite different. In the second

part the model is transformed into the language of

conceptual graphs. In the third one, there is a

summary algorithm presented for conversion of CG

in a related DTD.

2 STRUCTURED DOCUMENT

MODEL – A FORMAL

PRESENTATION

The information, which can be stored and

reproduced in an electronic format, is known as

document information. A document is assumed to be

a random text, stored on a holder as a single

information unit.

Every random text consists of a set of sentences,

which in turn consist of words. A sentence begins

with an upper-case letter and ends with a full stop,

denoting the end of it. A sentence with no words and

no ending point is an empty sentence. Sentences are

gathered together in logical structures, called

paragraphs. Each paragraph is a separate part of the

document. Paragraphs serve for separating

information into logically differentiated units. This

type of separation helps introduce a logical order in

a document, and process an information search.

Sentences exist only in paragraphs. A paragraph will

be called empty paragraph, if it consists of no

sentence or only empty sentences. The empty

paragraphs do not have information (meaningful)

contents. Therefore a document is an empty

document, if it consists of no paragraphs or only

empty paragraphs.

There are two document categories:

• Documents that have a predefined logical

order of their paragraphs

• free format documents, i.e. documents that

have no predefined logical order of their

paragraphs.

We are interested in creating a model for

documents, having a predefined logical order of

their paragraphs.

There is no exact definition for the term

structured document. There are only intuitive

assumptions, which are used depending on the

desired goals. For the goals of the present article we

shall introduce the following definitions:

Definition 1: A structured document is assumed

to be a document, for which the paragraphs can be

named and a relation ‘order’ is defined.

The relation ‘order’ applied for paragraphs can

be a strict one or a free one. Each document that has

paragraphs with a free order relation can be

transformed into a new document having a strict

order relation of the paragraphs by fixing the

paragraphs’ sequence. Paragraph naming and

paragraph ordering are called document labeling.

The document labeling consists in splitting up the

document into sets of tags, each of them consisting

of a part of the document text. Generally, repetition

of the same tags, consisting of the same part of the

text is allowable.

Let D be the set of structured documents.

Let X be the set of all elements (tags) for a given

set of documents D.

X = { nomenclature of elements (tags)

of a given document }

The tags are the metadata of a document. They

describe the document structure. This means that

every document can hold, besides its own

information tags, information part driven from outer

document of another type. Generally, the outer

document is not obligatory to be a structured one.

Hyperlinks can point toward a part of the document

itself.

Let T be the set of all paragraphs or texts for a

given set of documents D.

T = { paragraphs }

A document we assume to be a subset of the set

. Then for every document d that is a

member of the set

D it is true that . XTd ×⊆

We assign

to be the set containing the

separate tags of a given document.

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

∈∀= ∧ Ν∈ DX

d I, [1]

ICETE 2004 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

258

seqXX

[2]

NXX

[3]

The set

defines the type and the order of the

elements for each document

d. There is no

restriction that two different documents not have the

same elements order of the same type. A structured

document we assume to be a subset of the set

d is a document ( ), then d is a

structured document, if

XT ×

XTd ×⊆

We define the representation of the set

T in the

set

as a sequence of the partial functions:

XTd ×⊆

eqX

a [4]

We describe the structure and the text of a

random structured document

d by the set of partial

functions defined in eq. (4).

Let

be the elements of T. Then for each

document d, the text of the document is stored in the

elements of the set

⎪

⎭

⎪

⎬

⎫

⎪

⎨

∧ Ν∈∀= TT

tiit

⎪

⎩

Therefore

⎧

[5]

{}

dnddd

TtttTTT

ttt :,...,,

:,...,:,:

[6]

stores the text of a given document d. The whole

text of the document with the paragraphs order are

represented by

,...,:,:

dddd

XTXT

tt aa

{}

ddndd

seqXTtttXT

t aa :,...,,

[7]

3 REPRESENTATION OF A

STRUCTURED DOCUMENT

USING CONCEPTUAL GRAPHS

There are different models that can be used for

automatic processing of structured documents. Some

often-used models for structuring, storing and

processing of documents are: formatting languages

like SGML (Rubinsky, 1997) and XML (Hunter,

2000), textual DB, hypertext systems, etc.

We consider conceptual graphs in the terms

determined by Sowa (Sowa, 1984). A conceptual

graph is a net of conceptual and relational nodes.

Conceptual nodes present entities, attributes or

events. They are denoted with square brackets.

Relational nodes determine the type of the relation

between two conceptual nodes. They are denoted

with brackets (ISO, 2001).

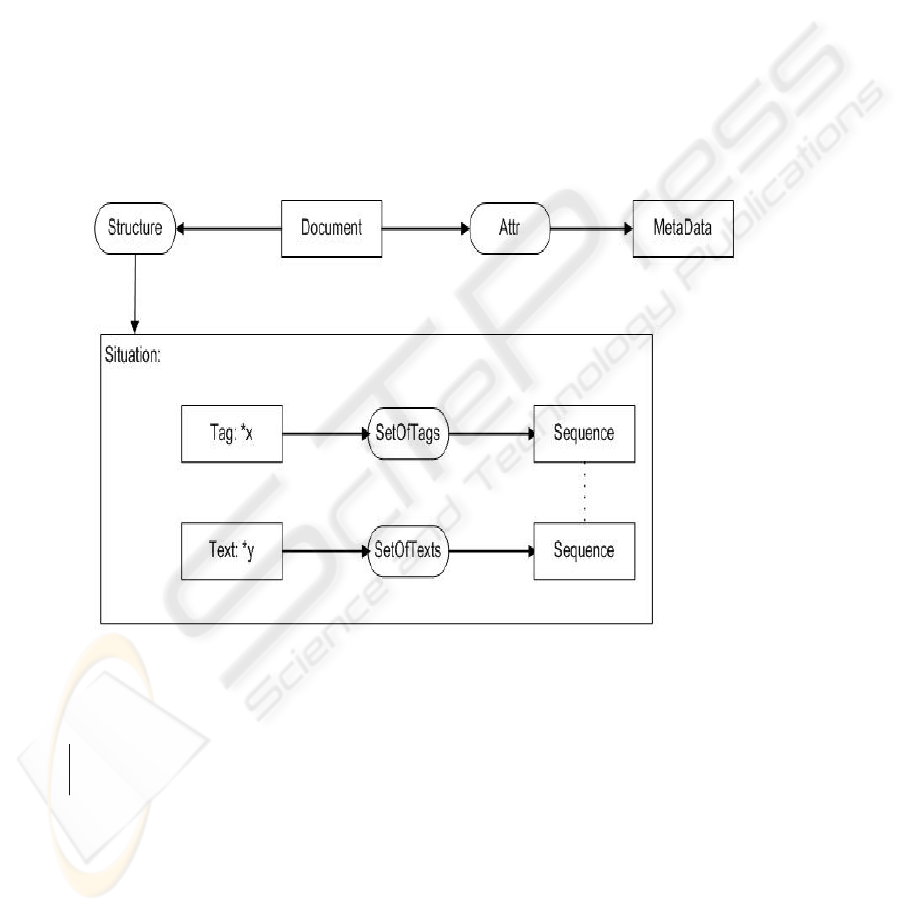
Figure1:A structure of a document represented by the usage of CG

The generated model is appropriate to be

presented by CG formalism. According to the

model, every structured document is an ordered set

of relations of the type:

<tag, text>

as the following restrictions are kept:

• Each text is presented only in a tag

• Each tag consists of either text, or tag, or is

empty

• Metadata for each document are described

with tags

With the above made assumptions, each textual-

based document can be represented by CG, as it is

shown in fig. 1.

STRUCTURED DOCUMENTS REPRESENTED BY CONCEPTUAL GRAPHS - A simple formalism for presenting

structured documents

259

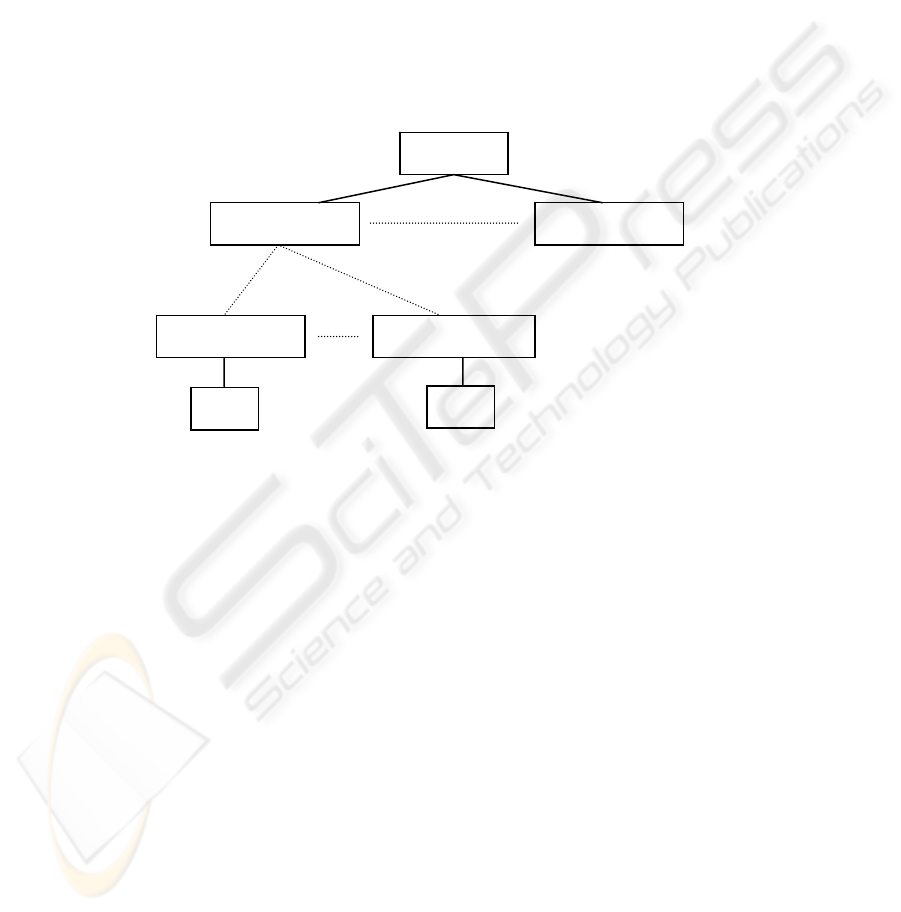
Figure 2: Hierarchy of types

For the formulated CG a hierarchy of types is

built, as it is shown on fig. 2

The description of the hierarchy types is as

follow:

1. Conceptual type

Tag. It represents the

elements of the set

X according to the

formulated model.

Type Tag is

[Tag: *x] –

´ (TagName) ´ [Name: ?x]

´ (Parent) ´ [Tag]

´ (Text) ´ [Text]

2. Conceptual type Text. It represents all the

texts of a document, i.e. the set T according to

the formulated model.

Type Text is

[Text: *x]

3. Conceptual type MetaData. It stores the

information for a document. Meta information

is stored in tags, which is analogous to the

storing of text in a document. The tags for

meta information are predefined.

Type MetaData is

[MetaData: *x]

´ (Attr) ´ [Tag: ?x]

4. Relational type SetOfTags. For each tag in

the document its parent is determined. In this

way a hierarchy of the tags is defined and as a

result a hierarchy of the document is defined

too.

Relation SetOfTags *x, *y is

[Tag: *x]

³ (Order) ³ [Sequence: ?y]

5. Relational type Structure. For each

document an order of its elements is

determined. An order set of relations of type

<tag, text> is defined. In this way the texts for

each tag of a document, with an already

defined structure, are set.

Relation Structure *x, *y, *z, *n is

[Document: ?x] -

´ (Attr) ´ [Tag: ?y]

´ (Attr) ´ [Text: ?z]

´ (Attr) ´ [Sequence: ?n]

6. Conceptual type Document. The document

d, according to the formulated model, is

presented as:

Type Document is

[Document: *x] –

´ (DocName) ´ [Name: ?x]

´ (Structure) ´ [Situation:

[Tag]

³ (SetOfTags) ³ [Sequence]

[Text]

³ (SetOfTexts) ³ [Sequence]

]

´ (Meta) ´ [MetaData]

Creating a CG for a concrete structured

document type, described with the presented model

is an algorithmical process. The algorithm for

presenting a structured document by CG is the

following one:

ICETE 2004 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

260

1. Create a CG for the declarative description of

tags and metadata of a document (the set

X).

2. Define a hierarchy for the already defined

conceptual types, i.e. the set

. The

hierarchy of the conceptual types defines the

document structure.

3. The texts of the document for the different

conceptual types are separated. The

separation of the texts for the different

concepts of the document could be made

automatically with a known precision.

4. There is an order relation created for the

conceptual types and their related texts. As a

result we get a structured presentation of a

document. The graphical representation of

document structure is shown on fig.3.

4 REPRESENTATION OF A

CONCEPTUAL GRAPH USING

XML

The document structure is described by CG. The

main purpose is the creation of DTD for a given

document type, described by CG. A valid XML is

generated from the created DTD. The text of the

XML document nodes is entered by a referent of the

relating conceptual types.

From the concept types and relation types

hierarchy a DTD is defined for the document types,

represented by CG as it is shown below:

1. To each concept type confront ELEMENT.

2. If concept type has Attr (attribute), which is a

text, i.e. the construction is like:

[Concept type] ´ (Attr) ´ [Text]

then we define the element as an element with

data, i.e.:

<!ELEMENT name (#PCDATA)>

3. If concept type has Attr (attribute), which is

not a text, i.e. the construction is like:

[Concept type] ´ (Thme) –

´ [Concept type 1]

……………………

´ [Concept type N]

then we define the element as an element with

sub-elements, i.e.:

<!ELEMENT name (ChildElement1, ….,

ChildElementN)>

4. A document type is defined, using the DTD

described above. A valid XML is generated

for it, using some of the specialized products

for XML generation, for example XMLSPY

(http://www.xmlspy.com), XMLwriter

(http://xmlwriter.net), etc.

5. The text of XML nodes is entered by a

referent in the conceptual nodes of CG. The

matching of XML nodes and CG nodes is

defined by the hierarchy of concept types.

As a result of the presented transformation, an

XML representation is produced for which a specific

structure is defined.

5 CONCLUSION

The article presented introduces a formal structured

document model. On the basis of the formulated

model there are conceptual types created for

Document

Tag 1 of level 1

Tag N of level 1

Tag 1 of level K Tag M of level K

Text

ure 3: A structured re

resentation of a document

STRUCTURED DOCUMENTS REPRESENTED BY CONCEPTUAL GRAPHS - A simple formalism for presenting

structured documents

261

describing the structure and the hierarchy of the

document. As a result, for each structured document

a DTD and the related XML description of the

document are generated. The presentation of a

random document with XML is not a trivial task.

The authors consider that the creation of a formal

description of documents is a step towards automatic

generation of documents structure.

REFERENCES

Calvanese, D, G. de Giacomo, M. Lenzerini, 1999,

Representing and Reasoning on XML Documents: A

Description Logic Approach, Journal of Logic and

Computation, Vol. 9, Issue 3, pp. 295-318.

Clarke, C, G. Cormack, F. Burkowski, 1994, An Algebra

for Structured Text Search and A Framework for its

Implementation, Technical Report CS-94-30,

University of Waterloo, Canada.

Groß-Hardt, M., 2002, Concept based querying of

semistructured data, Proceedings of the workshop

XML technology for the Semantic Web, Lecture Notes

in Informatics, Bonner Köllen Verlag.

Hunter, D., 2000, Beginning XML, Wrox Press.

ISO, 2001, Conceptual Graphs, Draft, ISO/JTC1/SC

32/WG2 N000.

Rubinsky, Y., M. Maloney, 1997, SGML on the Web,

Prentice Hall PTR.

Sowa, J., 1984, Conceptual Structures: Information

Processing in Mind and Machine, Addison Wesley,

Reading, Mass.

Louis, R., 1999. Software agents activities. In ICEIS’99,

1st International Conference on Enterprise

Information Systems. ICEIS Press.

ICETE 2004 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

262