
COMPRESSION OF HYPERSPECTRAL IMAGERY
VIA LINEAR PREDICTION
Francesco Rizzo, Bruno Carpentieri
Dipartimento di Informatica ed Applicazioni “R.M. Capocelli”, Università degli Studi di Salerno, Via S. Allende, Baronissi
(SA), Italy
Giovanni Motta, James A. Storer
Computer Science Department, Brandeis University, Waltham 02454 MA, USA
Keywords: Predictive Coding, Data Compression, Remote Sensing, 3D Data.
Abstract: (Motta et al., 2003) proposed a Locally Optimal Ve
ctor Quantizer (LPVQ) for lossless encoding of
hyperspectral data, in particular, Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) images. In this
paper we first show how it is possible to improve the baseline LPVQ algorithm via linear prediction
techniques, band reordering and least squares optimization. Then, we use this knowledge to devise a new
lossless compression method for AVIRIS images. This method is based on a low complexity, linear
prediction approach that exploits the linear nature of the correlation existing between adjacent bands. A
simple heuristic is used to detect contexts in which such prediction is likely to perform poorly, thus
improving overall compression and requiring only marginal extra storage space. A context modeling
mechanism coupled with a one band look ahead capability allows the proposed algorithm to match LPVQ
compression performances at a fraction of its space and time requirements. This makes the proposed method
suitable to applications where limited hardware is a key requirement, spacecraft on board implementation.
We also present a least squares optimized linear prediction for AVIRIS images which, to the best of our
knowledge, outperforms any other method published so far.
1 INTRODUCTION
In the last three decades, air-borne and space-borne
remote acquisition of high definition electro-optic
images has been increasingly used in military and
civilian applications to recognize objects and
classify materials on the earth’s surface. By
analyzing the spectrum of the reflected light it is
possible to recognize the material(s) composing the
observed scene. The development of new detector
technologies has made possible the introduction of
new classes of aircraft spectrometers capable of
recording a large number of spectral bands over the
visible and reflected infrared region. For this reason
the data sets they produce are often referred to as
hyperspectral. These instruments have reached
spectral resolution sufficient to allow very accurate
characterization of the spectral reflectance curve of a
given spatial area. For example, images acquired
with the JPL’s Airborne Visible/Infrared Imaging
Spectrometer, AVIRIS (NASA, 2003), have pixels
covering an area of approximately 20x20 meters,
with radiance decomposed into 224 narrow bands,
approximately 10nm wide each, in the range
400-2,500nm. Spectral components are represented
with a 16 bits precision.
Hyperspectral imagery is a rapidly growing
so
urce of remote sensed data, even though its
precision pales compared to the millions of channels
of a truly high resolution lab spectrometer. The
technology seems mature enough to use higher
resolution, space-borne spectrometers. In fact,
increasing the number of bands, i.e. the spectral
resolution, allows for more sophisticated analysis
and increases the data rate by only a linear amount.
The problem is that the acquisition of these images
already produces large amounts of highly correlated
317
Carpentieri B., Rizzo F., Motta G. and A. Storer J. (2004).
COMPRESSION OF HYPERSPECTRAL IMAGERY VIA LINEAR PREDICTION.
In Proceedings of the First International Conference on E-Business and Telecommunication Networ ks, pages 317-324
DOI: 10.5220/0001391703170324
Copyright
c
SciTePress

data (e.g., in the range 140-1,000 Mb for AVIRIS
images) in the form of a two dimensional image
matrix each pixel consisting of many components,
one for each spectral band (Figure 1).
Since hyperspectral imagery is acquired at cost
and often used in critical tasks like classification
(assignment of a label to every pixel) or target
detection (identification of a somewhat rare
instance), compression algorithms that provide
lossless or near-lossless quality (for classification
and detection purposes) may be required. In
addition, it may be desirable to have low complexity
that allows efficient on-board implementation with
limited hardware. Traditional approaches to the
compression of hyperspectral imagery are based on
differential prediction via DPCM (Aiazzi, 2001;
Abousleman, 1995; Abousleman et al., 2002), direct
vector quantization (Manohar and Tilton, 2000;
Ryan and Arnold, 1997; Mielikäinen and Toivanen,
2002; Pickering and Ryan, 2001) or dimensionality
reduction through Principal Component Analysis.
In (Motta et al., 2003) a locally optimal design of
a partitioned vector quantizer (LPVQ) for the
encoding of high dimensional data is presented. The
algorithm is applied to lossless, near-lossless and
lossy compression of AVIRIS data. LPVQ’s lossless
compression, is aligned with the current state of the
art. Its design and coding process, on the other hand,
are computationally intensive (although highly
parallelizable), while decoding is just table lookup.
The asymmetrical nature of the algorithm makes it
most appropriate for systems in which the codebook
design does not have to be performed on-board. An
inter-band linear prediction approach based on least
square optimization is presented in (Mielikäinen et
al., 2002). This compression method optimizes the
parameters of a linear predictor with spatial and
spectral support. Such optimization is performed for
each sample.
Using linear prediction, least square
optimization, and optimal band reordering, in
Section 2 we show how to encode efficiently the
quantization indices produced by LPVQ, improving
upon the baseline algorithm. We also exploit
successfully the fact that spectral correlation in the
original data is preserved in LPVQ indices after
quantization.
In Section 3 we target the linear nature of the
spectral correlation of AVIRIS data with a simple
linear prediction method. The proposed method is
composed by an intra-band predictor, similar to the
one in LOCO-I (Weinberger et al., 2000), for the
few bands with strong spatial correlation. The rest is
encoded using a novel inter-band predictor. This
predictor shares the same low complexity of the
intra-band one, and requires buffering of at most two
scan-lines from each of the previous three bands. It
also uses a simplified version of the context
modeling mechanism in LOCO-I that allows to
mach the compression performance of LPVQ.
Finally we discuss experimental results and current
research directions.
Figure 1: AVIRIS data cube Moffett Field, scene 1
(NASA, 2003)
2 IMPROVING ENTROPY
CODING OF LPVQ’S
QUANTIZATION INDICES
(Motta et al., 2003) compress hyperspectral data by
using a modified version of the Generalized Lloyd
Algorithm to perform a dimensionality reduction of
the original data. The D-dimensional input vectors
are broken into L sub–vectors (L=16 in the reported
experiments). Each sub–vector is then encoded with
the 8–bit index of the closest match in the codebook
generated by LPVQ, while the quantization error is
encoded separately. The spatial correlation in the
original data is preserved in the index files (planes),
so they look very much like “natural” grayscale
images. The index files are then encoded using
LOCO-I.
In this section we focus on improving the
compression of the quantization indices. We note
that spectral dependency is still observable among
index files. To take advantage of this phenomenon,
we propose three methods (summarized in Table 1)
two of which extend the LOCO-I/JPEG-LS
predictor. They compute the prediction, based on a
causal data subset (Figure 2),
kji
of the pixel
in the i-th row, j-th column of the k-th plane.
x
,,
ˆ
k
The first method in Table 1 is the one used by
LOCO-I, reported here as a reference. The second,
that we call INTER predictor, is similar to the one
presented in (Barequet an Feder, 1999), while
3D-MED is a novel, general extension of LOCO-I to
an inter-band context. These two methods share the
ji
x
,,
ICETE 2004 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
318

Table 1: linear predictors for encoding of LPVQ quantization indices.
),,Median(
ˆ
,1,1,,1,1,,,1,1,ILOCO kjikjikjikjikji
xxxxxx
−−−−−−−
−+=
),,Median(
ˆ
,3,2,1,2,11,,INTER kkkkkkji
DDDDDxx
−
+
+=
−
1,1,,1,,1 −−−
−=
kjikjik
xxD
, ,
1,,1,,1,2 −−−
−=
kjikjik
xxD
1,1,1,1,1,3 −−−−−
−=
kjikjik
xxD
)
,,,,Median(
1,,11,,,,1
,1,1,1,,,1,,1,1,,1,1,1,,,,1,1,MEDD3
−−−−
−−−−−−−−−−−−
−+
−
ˆ
+
−
+
=
kjikjikji
kjikjikjikjikjikjikjikjikji
xxx
xxxxxxxxxx
∑
=
−
=
j
jj
xx
1
LSQD3
ˆ
α
N
Figure 2: Prediction Template
same low complexity of the JPEG-LS standard, and
hence a highly efficient implementation is possible.
The third method, 3D-LSQ, is more aggressive
and computationally more expensive: given a
reference plane and a 3D subset of causal data, an
optimal linear predictor, in the least square sense, is
determined for each sample. The prediction structure
and the notation used in the following is similar to
the one presented in (Brunello et al., 2002).
Two different context enumerations are defined
based on the distance functions
Figure 3: 2D and 3D contexts and pixel enumerations
22
,,,,2
)()(),( qnpmxxd
kqpknmD
−+−=
⎪
⎩
⎪
⎨
≠−+−+
⎧
22
xx ≡
N
j
jxx ),0()0,0(
ˆ
α
=−+−
=
ijqnpm
ijqnpm
xxd
jqpinmD
22
,,,,3
)()(
4
1
)()(
),(
The resulting 2D and 3D context templates are
showed in Figure 3.
In the following, by
we denote the i-th pixel
in the above enumeration of the 2D context of
kji ,,
. Moreover, denotes the j-th pixel in the
3D context of
. The N-th order prediction of the
current pixel (
,, knm
, we drop the subscript
and the parenthesis when referring to the current
pixel) is computed as
)(ix
x
),( jix
)(ix
)0,0(
∑
=
⋅=
j
1
The coefficients
[
]
t
N
,,
10
minimizing
the energy of the prediction error
ααα
K=
M
ixixP
2
)0,(
ˆ
)0,(
()
∑
=
−=
i
1
are calculated using the well-known theory on
optimal linear prediction. Notice that the data used
in the prediction are a causal, finite sub–set of the
past data and no side information needs to be sent to
the decoder.
Using matrix notation, we write
)()( XCXC −⋅−=
αα
t
P
COMPRESSION OF HYPERSPECTRAL IMAGERY
319

where,
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎣
=
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎣
=
)0,(
),()1,( MxNMxMx
M
L
MOM XC
⎤
⎡
⎤
⎡
)0,1(),1()1,1( xNxx L
By taking the derivative with respect to
α
and
setting it to zero, the optimal predictor coefficients
are the solution of the following linear system
XCCC
tt
=⋅
0
)(
α
Once the optimal predictor coefficients for the
current sample have been determined, the prediction
error
⎣
xx
ˆ
−=
⎦
ε
is encoded in the same way of the
previous two methods.
3 OPTIMAL BAND ORDERING
Because each index file represents a subset of
contiguous spectral bands, and because the
correlation between two bands is not always
inversely proportional to the distance of their
wavelengths, a sequential encoding of the index files
is generally suboptimal. In order to address this
issue, given a function
representing the cost
of encoding plane j using plane i as reference, it is
possible to find the optimal plane ordering using
standard graph theory results. Similar ideas could be
find in (Tate, 1997; Motta and Weinberger, 2001).
()fij,
Given the cost
, we can define a complete
weighted graph with L nodes where the weight of
the edge
,ij
is equal to . We add a fictitious
node 0 connected by an edge to each node j. The
weight
,
()fij,
w
()fij,
j
w
0
represents the cost of encoding plane j
without using any reference plane (e.g., using
LOCO-I). The problem of optimal plane ordering is
equivalent to the problem of finding the minimum
spanning tree of the resulting graph (if
()fij
,
is not
symmetrical then the graph is directed and one
should compute the optimal branching rooted at
0
(Gabow et al., 1986)).
As a proof of concept, we used the first order
entropy of the difference between each pair of
planes as a cost function.
3.1 Context Modeling
The underlying assumption of the previous section is
that the index planes generated by LPVQ look very
much as “natural” images. This justifies the use of
off-shelf image-oriented techniques to encode these
data. This behavior is the by-product of the
lexicographical sorting of the centroids generated by
LPVQ, which are “scaled/translated” version of each
other. Similar behaviors are experienced in standard
VQ image compression when code-vectors are
arranged by increasing norm. This is not surprising
because if the VQ is not rate-distortion optimal (like
in most practical applications), then there must exist
some inter-codeword correlation. Given the structure
of LPVQ, there must be some correlation between
the codeword of adjacent sub-vectors as well, hence
the previous assumption is sub-optimal.
A lossless block coding of VQ code-vectors
specifically designed for image compression,
Address-VQ, was proposed in (Nasrabadi and Feng,
1990). Improvements were presented in (Wu et al.,
1998; Gong et al., 2000), which exploited the inter-
codeword correlations by means of context
modeling and conditional entropy. These methods
are off-line algorithms based on Bayes’ theorem
),(
)|,(
),|(
21
21
21
XXP
XXXP
XXXP =
where
X
is the VQ index to be coded,
1
X
and
2
X
causal neighbor of
X
).
The 3-dimensional nature of the LPVQ index
planes suggests the use of a 3-D causal context. In
order to assess the potentials of a Bayesian context
modeling scheme, we analyzed the empirical
probability
,, ,, 1 , 1, 1,,
()
i jk i jk i j k i jk
Px x x x
−− −
|
,−
, and
,, ,, 1
(
ijk ijk
Px x
−
)
|
for each index plane. In general, the
value of the pixel in the current plane is better
predicted by the value of the corresponding pixel in
the previous plane. This suggests a very simple,
on-line scheme named PREV: define 256 entropy
coders; encode
,,ijk
x
using the -th coder
(without any form of prediction).
,, 1ijk
x
−
proc PREV
def EC[256], EC1 as entropy_coder
; encode x
i,j,1
using EC1
EncodePlane(1,EC1)
for K = 2 to L do
for I = 1 to ROWS do
for J = 1 to COLS do
Encode(x
i,j,k
,EC[x
i,j,k-1
])
end proc
ICETE 2004 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
320
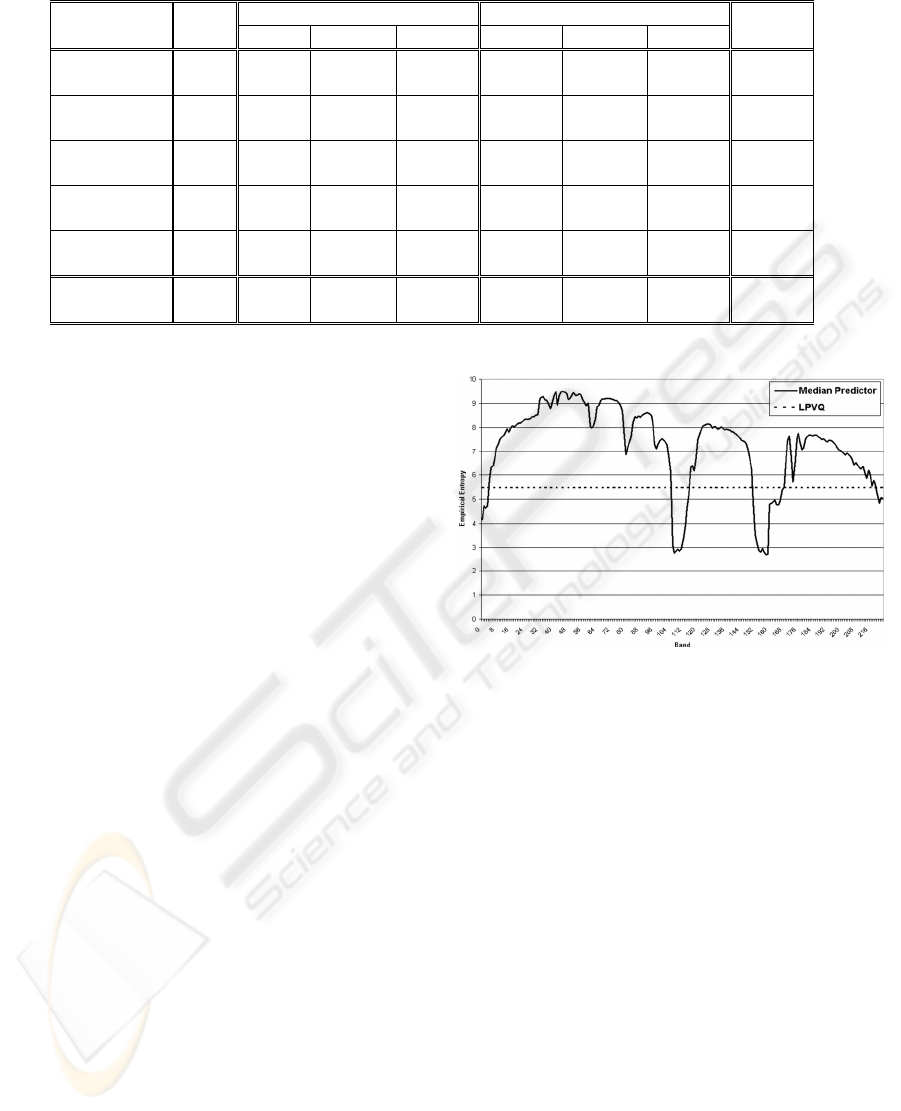
Table 2: entropy coding results for LPVQ indices.
Sequential Coding Optimal Band Ordering
LOCO
INTER 3D-MED 3D-LSQ INTER 3D-MED 3D-LSQ
PREV
43.44 44.97 48.82 47.30 46.11 50.28 50.52
Cuprite 40.44
+7.42% +11.19% +20.73% +16.96% +14.01% +24.33% +24.93%
35.99 37.75 39.13 38.06 38.39 39.88 47.31
Jasper Ridge 35.02
+2.77% +7.82% +11.76% +8.68% +9.64% +13.89% +35.09%
40.61 42.10 45.96 44.33 43.15 47.12 51.93
Low Altitude 39.10
+3.86% +7.67% +17.54% +13.38% +10.36% +20.52% +32.78%
46.30 48.00 51.22 49.42 48.91 52.38 57.72
LunarLake 44.45
+4.15% +7.99% +15.23% +11.18% +10.04% +17.85% +29.85%
43.35 44.28 47.34 46.53 45.28 48.76 55.70
Moffet Field 40.92
+5.92% +8.19% +15.67% +13.70% +10.65% +19.14% +36.12%
41.94 43.42 46.49 45.13 44.37 47.68 52.64
AVERAGE 39.99
+4.87% +8.59% +16.28% +12.86% +10.96% +19.25% +31.63%
3.2 Experimental results
Table 2 reports results in terms of compression far
all schemes presented so far. The reported results for
3D-LSQ are obtained with M=90 and N=9.
As expected, when sequential coding is used,
3D-LSQ is better than the 3D-MED and the INTER
predictor. Compared to the baseline LOCO-I coding,
on average the improvements attained are
respectively +16%, +8.54% and +4.87. When the
optimal plane ordering is in use, the improvements
are much higher (+19.25% for 3D-LSQ). More
interestingly, the PREV prediction/compression
scheme is more than 10% better than 3D-LSQ with
optimal ordering, and more than 30% better than
LOCO-I, used in (Motta et al., 2003). Furthermore,
PREV is more than
times faster than 3D-LSQ
on a AMD Athlon(tm) MP 1900+ based personal
computer.
200
4 INTER-BAND LINEAR
PREDICTION
Remote sensed images, like AVIRIS, show two
forms of correlation: spatial (the same material tends
to be present in many adjacent pixels: e.g., the water
of a river) and spectral (one band can be fully or
partially predicted from other bands). From our
investigations emerges that the spectral correlation is
generally much stronger than the spatial correlation.
Furthermore, dynamic range and noise levels
(instrument noise, reflection interference, aircraft
movements, etc.) of AVIRIS data are much higher
than those in photographic images. For these reasons
the spatial predictor of LOCO-I (Table 1) tends to
fail on this kind of data. Figure 4 shows the
performance in terms of bit per sample of this
predictor. From our simulations it is clear that the
median predictor of JPEG-LS is inefficient almost
everywhere, and especially in the visible part of the
spectrum that accounts for almost half of the data
and it is characterized by large dynamic ranges.
Nevertheless, JPEG-LS fast and efficient
compression would be highly desirable to an on-
board, hardware implementation.
Figure 4: Empirical band entropy of the Median
predictor
Motivated by these considerations, we propose a
novel compression method for AVIRIS data using a
a novel predictor for bands marked inter-band (IB
set) and a linear predictor in the style of JPEG-LS
for the rest.
This new predictor uses a simple heuristic to
detect contexts in which it is likely to fail. In such
cases the prediction is corrected using information
about the behavior of the inter-band predictor in the
previous two bands. After this prediction step, the
prediction error is computed and entropy coded with
a simple arithmetic coder. See Figure 5 for a formal
description. After the prediction step, the prediction
error is computed and entropy coded with a simple
arithmetic coder.
COMPRESSION OF HYPERSPECTRAL IMAGERY
321

⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
∉
≥−∈
⎥
⎦
⎥
⎢
⎣
⎢
−+−
+
<−∈
⎥
⎦
⎥
⎢
⎣
⎢
++
+−=
=
−
=
=
−−−−
=
=
IBkkjix
TDDIBk
fxfx
f
TDDIBk
DDD
xf
x
ILOCO
kd
d
kd
d
kjikjikjikji
kji
kd
d
kd
d
kkk
kjikji
kji
),,(
ˆ
)(min)(max,
2
)()(
)(min)(max,
3
1
ˆ
,
3,2,1
,
3,2,1
2,,1,,1,,1,,
,,
,
3,2,1
,
3,2,1
,3,2,1
,,,,
,,
Figure 5: Inter-Band Linear Predictor
4.1 Least Squares Optimization
In order to set an upper bound for the achievable
compression by the proposed linear prediction
method and for the data under examination, we
decided to implement a prediction scheme optimized
for each pixel and for each band based on least
squares optimization. We apply the 3D-LSQ (here
named SLSQ) approach of Section 2 directly to the
224 AVIRIS bands, rather than the 16 LPVQ index
planes, with M=4 and N=1.
The lossless compression results achieved by
this method on AVIRIS images are, at the best of
our knowledge, better than those published so far.
4.2 Experimental Results
Table 3 reports the compression ratio obtained by
LP and SLSQ on the five “standard” publicly
available AVIRIS images. We compare it with
JPEG-LS, JPEG2000 (Taubman and Marcellin,
2001), and LPVQ. We do not report the compression
results of (Mielikäinen et al., 2002) (claiming
average compression ratio of 3.06:1). This is
because their experimental results refer to a data sets
that seems to be a subset of the one we are using and
that we do not have currently available (furthermore
(Mielikäinen et al., 2002) reports non-standard
dimensions for AVIRIS images). LP has been
applied with IB=Σ-
{1…8}, where Σ is the set of
bands, and no prediction threshold. The proposed LP
method is comparable to LPVQ at a fraction of the
computational cost and it is sensibly superior to the
standard lossless image coders.
We also tested an extension of LP and SLSQ
based on the considerations taken from Figure 4. For
each scene of each cube (28 total) we checked which
band was better compressed spatially (LOCO-I)
rather than spectrally (LD/SLSQ). For any given
band i,
if and only if it has been compressed
in intra mode more than 15 times over 28 (HEU
option). A more aggressive approach (OPT) assumes
that the encoder checks for the best method first.
This requires virtually no side information (1
bit/band) and a one band look-ahead capability. For
LP we also introduced a simplified version of the
context modeling mechanism described in
(Weinberger et al., 2000), named LP-CTX.
IBi ∈
Results of improved algorithms are reported in
Table 4. We report also results of differential JPEG-
LS and differential JPEG2000, where by
“differential” we mean that the previous band is
subtracted from the current one for spectral
decorrelation before applying JPEG-LS or
JPEG2000. This pre-preprocessing steps improves
the two standard algorithms by 40% and 53%
respectively, but better compression is achieved by
LP and SLSQ. As we can see, the LP-CTX with on
band look-ahead improves by more than 2% the LP
method, matching LPVQ compression performance
at a cost of a small increase of storage requirements
over baseline LP, while being 5% better than
differential JPEG-LS/JPEG2000. Finally,
SLSQ-OPT achieves the overall best compression.
While this method needs a one band look-ahead, it
has the advantage of requiring virtually no side
information (1 bit/band), and since inter and intra
mode could be performed in parallel, compression
time is practically unchanged.
5 CONCLUSIONS
In the first part of this paper we present and analyze
three linear prediction schemes for the encoding of
the index planes generated by the LPVQ algorithm.
The best method achieves ≈20% improvement upon
the basic schemes presented in (Motta et al., 2003).
In the final subsection we show that the assumption
that the index planes are comparable to “natural”
images is not completely true. We also show how a
very simple context modeling can achieve even
better compression.
In the second part of the paper we propose a
novel approach for lossless coding of AVIRIS data.
It is based on an inter-band, linear predictor that,
coupled with a simple entropy coder, competes with
the current state of the art. The low complexity of
the proposed method and its raster scan nature,
makes it amenable for on-board implementations.
Since the proposed method depends loosely on
the entropy coder, it would be also possible to
remove the arithmetic coder and use the CCSDS
standard algorithm for lossless data compression for
space applications (CCSDS, 1997), whose hardware
implementation is widely used on many satellites.
ICETE 2004 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
322

Table 3: Compression Results.
JPEG-LS JPEG2000 LPVQ LPVQ-PREV LP SLSQ
Cuprite 2.09 1.91 3.13 3.18 3.03 3.15
Jaspder Ridge 2.00 1.80 2.82 2.88 2.94 3.15
Low Altitude 2.14 1.96 2.89 2.94 2.76 2.98
Lunar Lake 1.99 1.82 3.23 3.28 3.05 3.15
Moffett Field 1.91 1.78 2.94 3.00 2.88 3.14
AVERAGE 2.03 1.85 3.00 3.06 2.93 3.12
Table 4: Improvements of baseline LP and SLSQ algorithms.
LP-CTX SLSQ
Differential
JPEG-LS
Differential
JPEG2000
IB =
Σ-{1…8}
60% OPT 60% OPT
Cuprite 2.91 2.92 3.04 3.07 3.09 3.23 3.24
Jasper Ridge 2.81 2.82 2.96 2.98 3.00 3.22 3.23
Low Altitude 2.70 2.69 2.79 2.79 2.83 3.02 3.04
Lunar Lake 2.93 2.94 3.06 3.08 3.10 3.23 3.23
Moffett Field 2.84 2.83 2.93 2.94 2.96 3.20 3.21
AVERAGE 2.84 2.84 2.96 2.97 3.00 3.18 3.19
We are currently working to improve the
inter-band predictor and perform a formal analysis
of the remaining correlation after prediction, in order
to find suitable context modeling mechanisms that
will indubitably improve current performances.
Near-lossless extensions are also under
consideration.
REFERENCES
Abousleman, G. P. (1995). Compression of hyperspectral
imagery using hybrid DPCM/DCT and entropy
constrained trellis coded quantization. In Storer, J. A.
and Cohn, M., editors, Proceedings Data Compression
Conference, pages 322–331. IEEE Computer Society
Press.
Abousleman, G. P., Lam, T.-T., and Karam, L. J. (2002).
Robust hyperspectral image coding with
channeloptimized trellis-coded quantization. IEEE
Transactions on Geoscience and Remote Sensing,
40(4):820–830.
Aiazzi, B., Alparone, L., and Baronti, S. (2001).
Nearlossless compression of 3-D optical data. IEEE
Transactions on Geoscience and Remote Sensing,
39(11):2547–2557.
Barequet, R. and Feder, M. (1999). SICLIC: A simple
intercolor lossless image coder. In Storer, J. A. and
Cohn, M., editors, Proceedings of the Data
Compression Conference, pages 501–510, Snowbird,
Utha. IEEE Computer Society Press.
Brunello, D., Calvagno, G., Mian, G. A., and Rinaldo, R.
(2002). Lossless video coding using optimal 3D
prediction. In Proceedings of the 9th IEEE
International Conference on Image Processing (ICIP
2002), volume 1, pages 89–92, Rochester, NY. IEEE
Signal Processing Society.
CCSDS (1997). Consulting Committee for Space Data
Systems, ”Recommendation for space data system
standards: Lossless data compression”. CCSDS
121.0-B-1, Blue Book.
Gabow, H. N., Galil, Z., Spencer, T., and Tarjan, T. R.
(1986). Efficient algorithms for finding minimum
spanning trees in undirected and directed graphs.
Combinatorica, 6(2):109–122.
Gong, Y., Fan, M. K. H., and Huang, C.-M. (2000). Image
compression using lossless coding on VQ indexes. In
Storer, J. A. and Cohn, M., editors, Proceedings of the
Data Compression Conference, page 583, Snowbird,
Utha. IEEE Computer Society Press.
Manohar, M. and Tilton, J. C. (2000). Browse level
compression of AVIRIS data using vector quantization
on massively parallel machine. In Proceedings AVIRIS
Airborne Geoscience Workshop.
Mielikäinen, J., Kaarna, A., and Toivanen, P. (2002).
Lossless hyperspectral image compression via linear
prediction. Proceedings of SPIE, 4725(8):600–608.
Mielikäinen, J. and Toivanen, P. (2002). Improved vector
quantization for lossless compression of AVIRIS
images. In Proceedings of the XI European Signal
Processing Conference, EUSIPCO-2002, Toulouse,
France. EURASIP.
Motta, G., Rizzo, F., and Storer, J. A. (2003). On the
compression of hyperspectral imagery. In Storer, J. A.
and Cohn, M., editors, Proceedings of the Data
Compression Conference, Snowbird, Utha. IEEE
Computer Society Press.
Motta, G. and Weinberger, M. J. (2001). Compression of
polynomial texture maps. Technical Report 143 (R.2),
HP Laboratories Palo Alto.
NASA (2003). AVIRIS home page.
http://popo.jpl.nasa.gov.
COMPRESSION OF HYPERSPECTRAL IMAGERY
323

Nasrabadi, N. M. and Feng, Y. (1990). Image compression
using address-vector quantization. IEEE Transactions
on Communication, 38:2166–2173.
Pickering, M. and Ryan, M. (2001). Efficient
spatialspectral compression of hyperspectral data.
IEEE Transactions on Geoscience and Remote
Sensing, 39(7):1536–1539.
Ryan, M. J. and Arnold, J. F. (1997). The lossless
compression of AVIRIS images by vector
quantization. IEEE Transactions on Geoscience and
Remote Sensing, 35(3):546–550.
Tate, S. R. (1997). Band ordering in lossless compression
of multispectral images. IEEE Transactions on
Computers, 46:477–483.
Taubman, D. and Marcellin, M. W. (2001). Jpeg2000:
Image Compression Fundamentals, Standards, and
Practice. Kluwer Academic Publishers, Boston, MA.
Weinberger, M. J., Seroussi, G., and Sapiro, G. (1996).
LOCO-I: A low complexity, context-based, lossless
image compression algorithm. In Storer, J. A. and
Cohn, M., editors, Proceedings of the Data
Compression Conference, pages 140–149, Snowbird,
Utha. IEEE Computer Society Press.
Wu, X., Barthel, K. U., and Zhang, W. (1998). Piecewise
2D autoregression for predictive image coding. In
Proceedings of the International Conference on Image
Processing (ICIP 1998), volume 3, pages 901–904.
IEEE Signal Processing Society.
ICETE 2004 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
324
