
PACKET SCHEDULING FOR MAXIMIZING REVENUE IN A
NETWORK NODE
Jian Zhang, Timo H
¨
am
¨
al
¨
ainen, Jyrki Joutsensalo
Dept. of Mathematical Information Technology
University of Jyv
¨
askyl
¨
a, FIN-40014 Jyv
¨
askyl
¨
a, Finland
Keywords:
Packet scheduling, QoS, pricing, revenue maximization.
Abstract:
In the future Internet, different applications such as Voice over IP (VoIP) and Video-on-Demand (VoD) arise
with different demands on Quality of Service (QoS). Different kinds of service classes (e.g. gold, silver,
bronze) should be supported in a network node. In the network node, packets are queued using a multi-
queue system, where each queue corresponds to one service class. The customers of different classes will pay
different prices to network providers based on multi-class pricing models. In this paper, we considered the
optimization problem of maximizing the revenue attained in a network node under linear pricing scenario. A
revenue-aware scheduling approach is introduced, which has the closed-form solution to the optimal weights
for revenue maximization derived from revenue target function by Lagrangian optimization approach. The
simulations demonstrate the revenue maximization ability of our approach.
1 INTRODUCTION
Integrated packet switched service networks must
carry a wide range of different traffic types being
still able to provide performance guarantees to real-
time sessions such as Voice over IP (VoIP), Video-
on-Demand (VoD), or video-conferencing. Efficient
and effective communication needs careful Quality of
Service (QoS) design in the future multi-service In-
ternet. In QoS design, different demands of different
types of traffic classes (VoIP, VoD etc.) and different
prices paid by different classes (gold, silver, bronze
etc.) must be taken into account for giving plausible
and fair service.
Packet scheduling discipline is an important fac-
tor of a network node. The choice of the discipline
impacts the allocation of restricted network resources
among competing sessions of the communication net-
work. On the other hand, network operators can
handle resource reservations by using traffic differ-
entiation and design different kind of pricing strate-
gies for customers with different service classes. The
open question still arises: how to put these two is-
sues together. Pricing research in the networks has
been quite intensive during the last few years (e.g.,
(Mackie-Mason et al, 1994), (Kelly, 1994), (Kelly,
1997), (Kelly et al, 1998), (Courcoubetis et al, 2000),
(Paschalidis et al, 2000), (La et al, 2002), (Pascha-
lidis et al, 2002)) and also novel fair scheduling algo-
rithms have been proposed (e.g., (Parekh et al, 1993),
(Golestani, 1994), (Stiliadis et al, 1995), (Stiliadis et
al, 1996)), but combination of them have not been an-
alyzed widely.
Our research differs from the above studies by link-
ing pricing and queuing issues together and allocat-
ing network resources among competing sessions in
the context of revenue maximization. In a network
node, packets are queued using a multi-queue sys-
tem, where each queue corresponds to one service
class. The customers of different classes will pay
different prices to network providers based on multi-
class pricing models. In this paper, we considered
the optimization problem of maximizing the revenue
attained in a network node under linear pricing sce-
nario. A revenue-aware scheduling approach is intro-
duced, which has the closed-form solution to the op-
timal weights for revenue maximization derived from
revenue target function by Lagrangian optimization
approach. The simulations demonstrate the revenue
maximization ability of our approach.
The rest of the paper is organized as follows. In
Section 2, three pricing scenarios (linear, flat and
piecewise linear) are presented and the linear one
is generally defined. Revenue-aware scheduling ap-
134
Zhang J., Hämäläinen T. and Joutsensalo J. (2004).
PACKET SCHEDULING FOR MAXIMIZING REVENUE IN A NETWORK NODE.
In Proceedings of the First International Conference on E-Business and Telecommunication Networks, pages 134-139
DOI: 10.5220/0001392601340139
Copyright
c
SciTePress
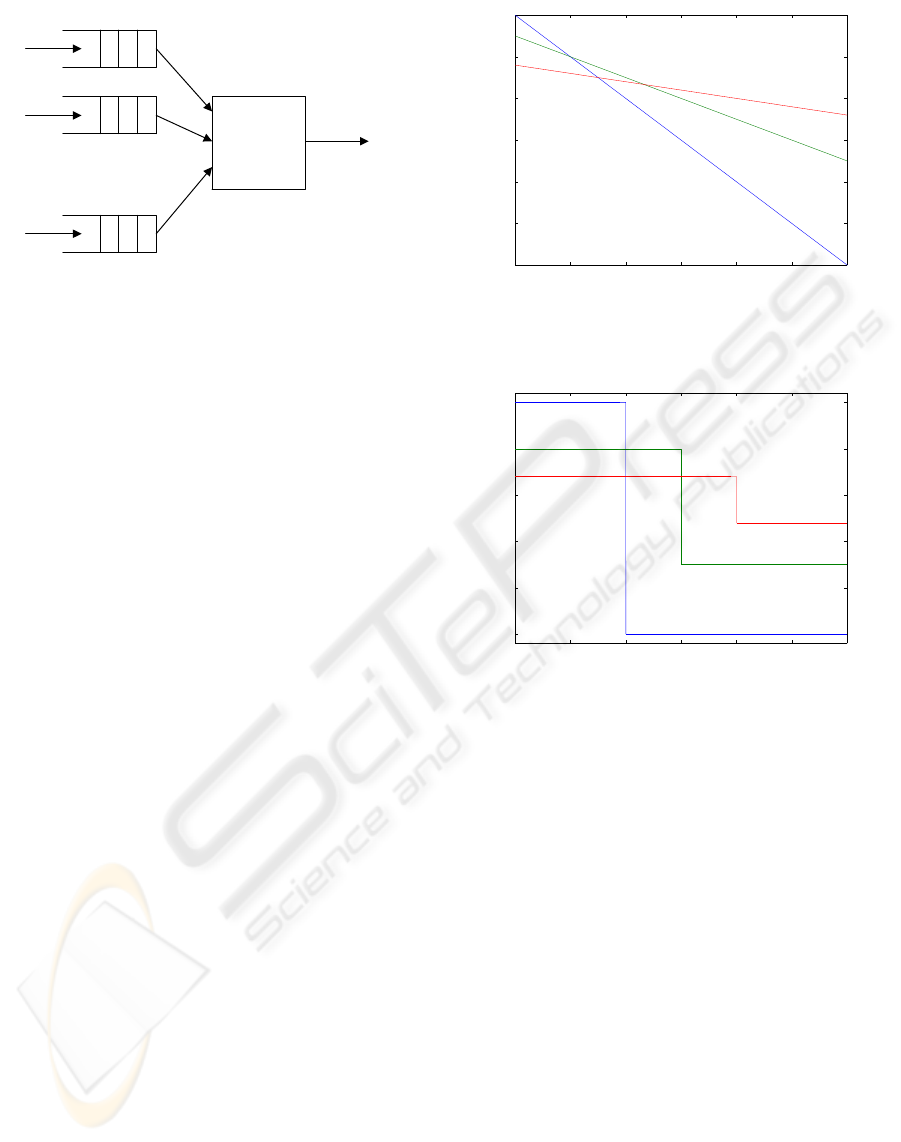
. . .
CLASS 1
CLASS 2
CLASS m
w1
w2
wm
OUTPUT
lambda 1
lambda 2
lambda m
PACKET
SCHEDULER
Figure 1: Traffic classification at the packet scheduler
proach is derived in Section 3, where the closed-
form solution to the optimal weights is presented in
the context of revenue maximization and the analytic
maximum revenue is also derived. Section 4 contains
simulation part demonstrating the revenue maximiza-
tion ability of our approach. Finally, in Session 5, we
present concluding remarks.
2 PRICING SCENARIO
Here three simple pricing scenarios are presented and
we believe that they are also the most used ones. First
some parameters and notions are defined. Let d
0
be the minimal processing time of the scheduler for
transmitting 1-bit data from one queue to the output in
Fig. 1, i.e., d
0
= 1/C if the processing capacity of the
scheduler is C bits/s. The number of service classes
is denoted by m. Literature usually refers to the gold,
silver and bronze classes; in this case, m = 3. The
mean delay for class i during one measurement pe-
riod is referred to as
¯
d
i
. For each service class, a pric-
ing function r
i
(
¯
d
i
) will be defined to rule the relation-
ship between the QoS provided by network providers
(mean delay in this case) and the payment of their cus-
tomers (revenue/penalty in this paper). Obviously, it
is non-increasing with respect to its mean delay
¯
d
i
.
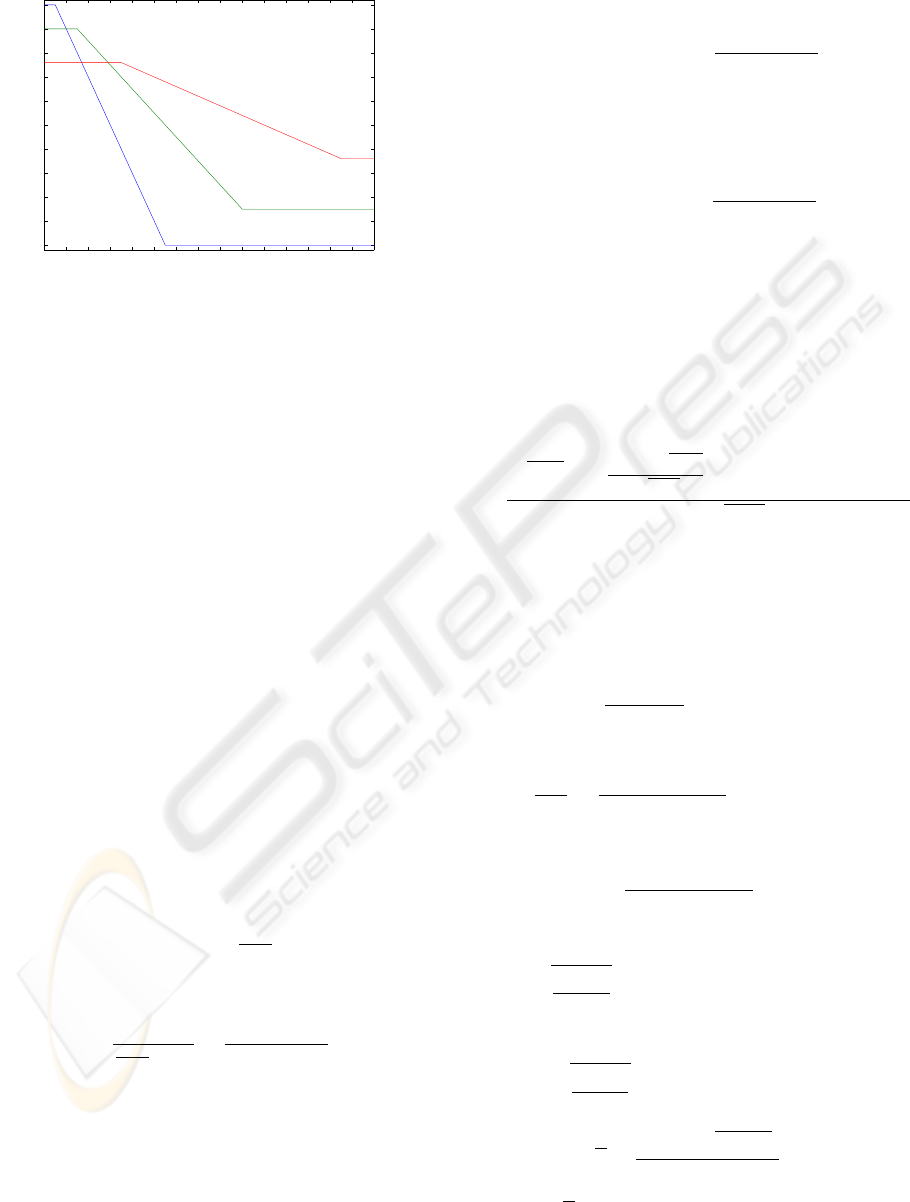
Examples of pricing functions are given in Figs. 2, 3,
and 4, which show the most used pricing strategies:
linear, flat and piecewise linear models, respectively.
In this paper, our study concentrates on the revenue-
maximizing issue under linear pricing functions and
the analysis under flat pricing strategy is postponed to
its sequel. The solution to the piecewise linear pricing
model is a straightforward extension to the above two
ones. Specifically, Linear pricing model for class i is
characterized by the following definition.
Definition 1: The function
r
i
(
¯
d
i
) = b
i
− k
i
¯
d
i
, i = 1, 2, ..., m, b
i
> 0, k
i
> 0
(1)
0 10 20 30 40 50 60
−400
−300
−200
−100
0
100
200
mean delay
revenue
Linear pricing functions
Figure 2: Three linear pricing functions. Horizontal axis:
mean delay; vertical axis: price.
0 10 20 30 40 50 60
−150
−100
−50
0
50
100
mean delay
revenue
Flat pricing functions
Figure 3: Three flat pricing functions. Horizontal axis:
mean delay; vertical axis: price.
is called linear pricing function, where b
i
and k
i
are
positive constants and normally b
i
≥ b
j
and k
i
≥
k
j
hold to ensure differentiated pricing if class i has
higher priority than class j (in this paper, we assume
that class 1 is the highest priority and class m is the
lowest one).
Fig. 2 depicts three linear pricing functions for
gold, silver and bronze classes and it is commented
more detailed below. For gold class, the pricing func-
tion r
1
(
¯
d
1
) = 200 − 10
¯
d
1
means that when its mean
delay
¯
d
1
is small, the price paid by gold class cus-
tomers is high - in this case, maximally 200 units
of money. It is natural that for the highest priority
class, constant shift b
1
is selected to be the highest.
On the other hand, penalty paid to the highest pri-
ority class customers is also highest if the scheduler
fails to meet its minimum requirement of mean delay
(20 time units in this case) and the growing rate of
penalty along with mean delay depends on the slope
k
1
(highest in this case). For example, if
¯
d
1
= 30,
then r
1
(
¯
d
1
) = r
1
(30) = 200 − 10 ∗ 30 = −100,
i.e., the penalty is 100 units of money. Same obser-
PACKET SCHEDULING FOR MAXIMIZING REVENUE IN A NETWORK NODE
135
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150
−300
−250
−200
−150
−100
−50
0
50
100
150
200
mean delay
revenue
Piecewise linear pricing functions
Figure 4: Three piecewise linear pricing functions. Hori-
zontal axis: mean delay; vertical axis: price.
vations hold for silver and bronze classes. For bronze
class, r
3
(
¯
d
3
) = 80 −2
¯
d
3
means that the price paid by
that class customers is maximally 80 units of money.
In this case, constant shift b
3
is lowest. On the other
hand, the growing rate of penalty for bronze class will
also be lowest since its slope k
3
= 2 is the lowest.
3 REVENUE MAXIMIZATION
APPROACH
Let us consider a packet scheduler fed by m Poisson
streams with arrival rates λ
1
, λ
2
, ..., λ
m
as shown in
Fig. 1. We assume that in this paper the distribution
of packet length in all classes is exponential and use
¯
L
i
to denote the mean packet size in bits in class i.
Let the weight allotted to class i be w
i
, i = 1, 2, ..., m.
Without loss of generality, only non-empty queues are
considered, and thus w
i
6= 0. If some weight w
i
= 1,
then m = 1. Therefore, the natural constraint for the
weights is
P
m
i=1
w
i
= 1, w
i
∈ (0, 1]. If the weight
assigned to class i is w
i
, class i in the scheduler can
be guaranteed to have a share of processing capac-
ity w
i
/d
0
(bits/s) and mean service time of packets
in class i can be estimated by
¯
L
i
d
0
w
i
; hence, the ana-
lytic form of mean delay
ˆ
¯
d
i
for class i packet can be
denoted as
ˆ
¯
d
i
=
1
w
i
¯
L
i
d
0
− λ
i
=
¯
L
i
d
0
w
i
− λ
i
¯
L
i
d
0
(2)
based on queueing theory. The natural constraint for
Eq. (2) is w
i
> λ
i
¯
L
i
d
0
due to the fact that delay can
not be negative.
We use the analytic form
ˆ
¯
d
i
in Eq. (2) to estimate
the real mean delay of class i packet
¯
d
i
during one
measurement period and define F to be the revenue
gained in a network node during that period as follows
when the linear pricing function in Eq. (1) is used:
F =
m
X
i=1
r
i
(
¯
d
i
) =
m
X
i=1
(b
i
−
k
i
¯
L
i
d
0
w
i
− λ
i
¯
L
i
d
0
) (3)
As a result of the above definition, the issue of rev-
enue maximization in a packet scheduler can be for-
mulated as follows:
max F =
m
X
i=1
(b
i
−
k
i
¯
L
i
d
0
w
i
− λ
i
¯
L
i
d
0
) (4)
s.t.
m
X
i=1
w
i
= 1, 0 < w
i
≤ 1 (5)
w
i
> λ
i
¯
L
i
d
0
(6)
.
Theorem 1 For linear pricing functions, the globally
maximum revenue F is achieved by using the follow-
ing optimal weight
w
i
=
p
k
i
¯
L
i
(1 +
P
m
j=1
√
k
j
¯
L
j
√
k
i
¯
L
i
λ
i
¯
L
i
d
0
−
P
m
j=1
λ
j
¯
L
j
d
0
)
P
m
j=1
p
k
j
¯
L
j
,
i = 1, 2, ..., m (7)
and it is unique when w
i
∈ (0, 1].
Proof: Based on Equations (4) and (5), we can con-
struct the following Lagrangian equation.
P = P (w
1
, w
2
, ..., w
m
)
=
P
m
i=1
(b
i
−
k
i
¯
L
i
d
0
w
i
−λ
i
¯
L
i
d
0
) + σ(1 −
P
m
i=1
w
i
) (8)
Set partial derivatives of P in Eq. (8) to zero:
∂P
∂w
i
=
k
i
¯
L
i
d
0
(w
i
− λ
i
¯
L
i
d
0
)
2
− σ = 0. (9)
It follows that
σ =
k
i
¯
L
i
d
0
(w
i
− λ
i
¯
L
i
d
0
)
2
(10)
leading to the solution
w
i
=
r
k
i
¯
L
i
d
0
σ
+ λ
i
¯
L
i
d
0
, i = 1, 2, ..., m. (11)
Substituting Eq. (11) to Eq. (5), we get
m
X
i=1
r
k
i
¯
L
i
d
0
σ
+
m
X
i=1
λ
i
¯
L
i
d
0
= 1
√
σ =
P
m
i=1
p
k
i
¯
L
i
d
0
1 −
P
m
i=1
λ
i
¯
L
i
d
0
(12)
And when
√
σ in Eq. (12) is substituted to Eq. (11),
the closed-form solution in Eq. (7) is obtained.
ICETE 2004 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS
136

Because of the constraint in Eq. (6) w
i
> λ
i
¯
L
i
d
0
,
obviously,
m
X
j=1
w
j
= 1 >
m
X
j=1
λ
j
¯
L
j
d
0
(13)
Hence, the closed-form solution in Eq. (7) w
i
> 0.
Moreover, based on (13), the following inequality
holds
λ
i
¯
L
i
d
0
−
p
k
i
¯
L
i
P
m
j6=i
j=1
λ
j
¯
L
j
d
0
P
m
j6=i
j=1
p
k
j
¯
L
j
≤ 1
leading to in Eq. (7) the numerator less than the de-
nominator. Hence, we can conclude that 0 < w
i
≤ 1.
To prove that the closed-form solution in Eq. (7)
is the only and optimal one in the interval (0, 1], we
consider second order derivative of P.
∂
2
P
∂w
2
i
= −
2k
i
¯
L
i
d
0
(w
i
− λ
i
¯
L
i
d
0
)
3
< 0 (14)
due to the constraint w
i
> λ
i
¯
L
i
d
0
in (6). Therefore,
the revenue F gained by a network provider is strictly
concave in the interval 0 < w
i
≤ 1, having one
and only one maximum. This completes the proof.
Q.E.D.
Analytical form of the maximum revenue gained
during a measurement period can be expressed by the
optimal weights given in Eq. (7).
.
Theorem 2 When the optimal weights are used ac-
cording to Theorem 1, the analytic value of maximum
revenue obtained in a network node during the mea-
surement period is
F
max
=
m
X
i=1
b
i
−
(
P
m
i=1
p
k
i
¯
L
i
)
2
d
0
1 −
P
m
i=1
λ
i
¯
L
i
d
0
(15)
Proof: When the optimal weights in Eq. (7) are sub-
stituted to Eq. (3), the maximum revenue obtained is
F
max
=
m
X
i=1
(b
i
−
k
i
¯
L
i
d
0
P
m
i=1
p
k
i
¯
L
i
p
k
i
¯
L
i
(1 −
P
m
i=1
λ
i
¯
L
i
d
0
)
)
=
m
X
i=1
(b
i
−
d
0
p
k
i
¯
L
i
P
m
i=1
p
k
i
¯
L
i
1 −
P
m
i=1
λ
i
¯
L
i
d
0
)
=
m
X
i=1
b
i
−
(
P
m
i=1
p
k
i
¯
L
i
)
2
d
0
1 −
P
m
i=1
λ
i
¯
L
i
d
0
Q.E.D.
4 SIMULATIONS
In this section we present some simulation results to
illustrate the effectiveness of our approach for max-
imizing revenues under linear pricing functions. A
number of simulations have been conducted under
different parameter settings. In each case, we numer-
ically determine the optimal solutions using Theorem
1 and 2, and then we investigate through simulation
the benefits of our approach by comparing the rev-
enues obtained under our optimal weights with those
obtained under a natural scheme of proportional as-
signment. A representative set of these simulations
are presented herein. Throughout this section, we
shall focus on a packet scheduler with the number
of service classes m = 3 (namely, gold, silver and
bronze classes) and minimum processing time d
0
=
10
−6
s. The base arrival rates and the mean packet
sizes for three classes are provided in Table 1. A mul-
tiplicative load factor ρ > 0 is used to scale these
base arrival rates to consider different traffic intensi-
ties; i.e., λ
j
ρ is used in the simulations for class-j ar-
rival rate. As previously noted, we use a scheme that
proportionally allocates the weight among all service
classes for comparison with our revenue-maximizing
approach. Specifically, the proportional scheme as-
signs the weight for class i as follows:
w
i
=
λ
i
¯
L
i
P
m
j=1
(λ
j
¯
L
j
)
, i = 1, 2, ..., m. (16)
Note that this proportional assignment scheme is a
natural way to allocate the scheduler processing ca-
pacity.
Table 1: The base parameters for packet traffic
i = 1 i = 2 i = 3
(gold class) (silver class) (bronze class)
λ
i
10 15 20
(packets/s)
¯
L
i
(bits)
3360 3360 3360
4.1 The first set of simulations
In the first set of simulations, the parameters related
to three linear pricing functions used are summarized
as follows: b
1
= 200, k
1
= 10000, for gold class,
b
2
= 150, k
2
= 5000, for silver class, and b
3
= 80,
k
3
= 2000, for bronze class (note that the time unit is
second here).
First we investigate the evolution of the revenue
along with the time under our optimal weights and
the proportional weights. In this case, the base arrival
rates in Table 1 are used and one set of given weights
(w
1
= 0.60, w
2
= 0.25, w
3
= 0.15) is also used
for comparison with our approach. Fig. 5 presents
the simulation results, where the x-axis represents the
time (the measurement period is 100 seconds here)
and the y-axis represents the revenue obtained during
PACKET SCHEDULING FOR MAXIMIZING REVENUE IN A NETWORK NODE
137
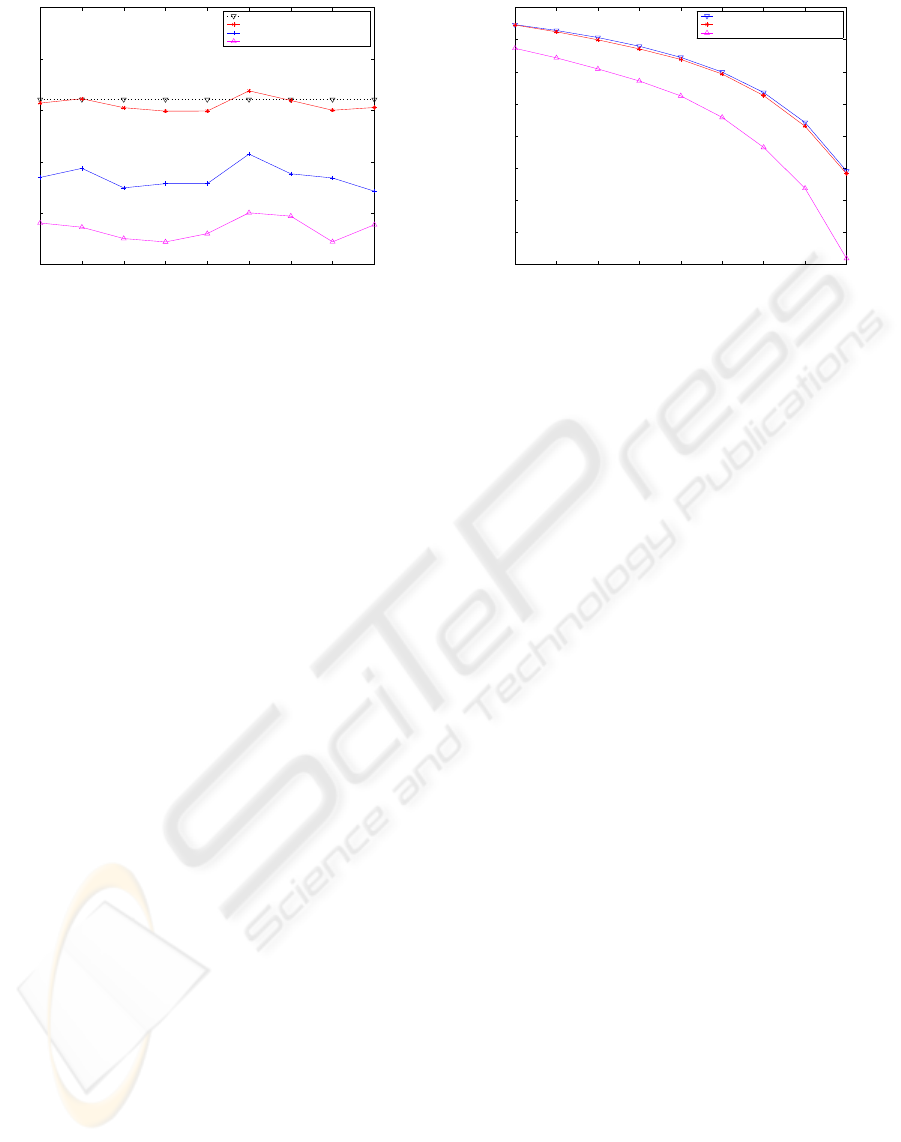
100 200 300 400 500 600 700 800 900
150
180
210
240
270
300
time (s)
revenue
Analytic
Simulated under optimal weights
Simulated under given weights
Simulated under proportional weights
Figure 5: Revenue comparison as function of time, for the
case, load factor ρ = 1 and b
1
= 200, k
1
=10000, b
2
= 150,
k
2
= 5000, b
3
= 80, k
3
= 2000.
that measurement period. Unless stated otherwise, we
shall hereafter refer to the latter as revenue. It is ob-
served that the largest revenue is achieved under our
optimal weights compared with those achieved un-
der the proportional and given weights and it is quite
close to the analytic value of maximum revenue by
Eq. (15). Since the parameters used in Eq. (15) are
constant in this case, the analytic value remains con-
stant; whereas, for the mean delay of packets by simu-
lations is variable, the simulated revenue varies along
with the time. Fig. 5 shows that the revenue obtained
under our optimal weights is very close to the ana-
lytic value, which demonstrates the effectiveness of
our approach for revenue maximization.
Next we examine the performance of our revenue-
maximizing approach for the case that the same pric-
ing functions are used and different traffic intensi-
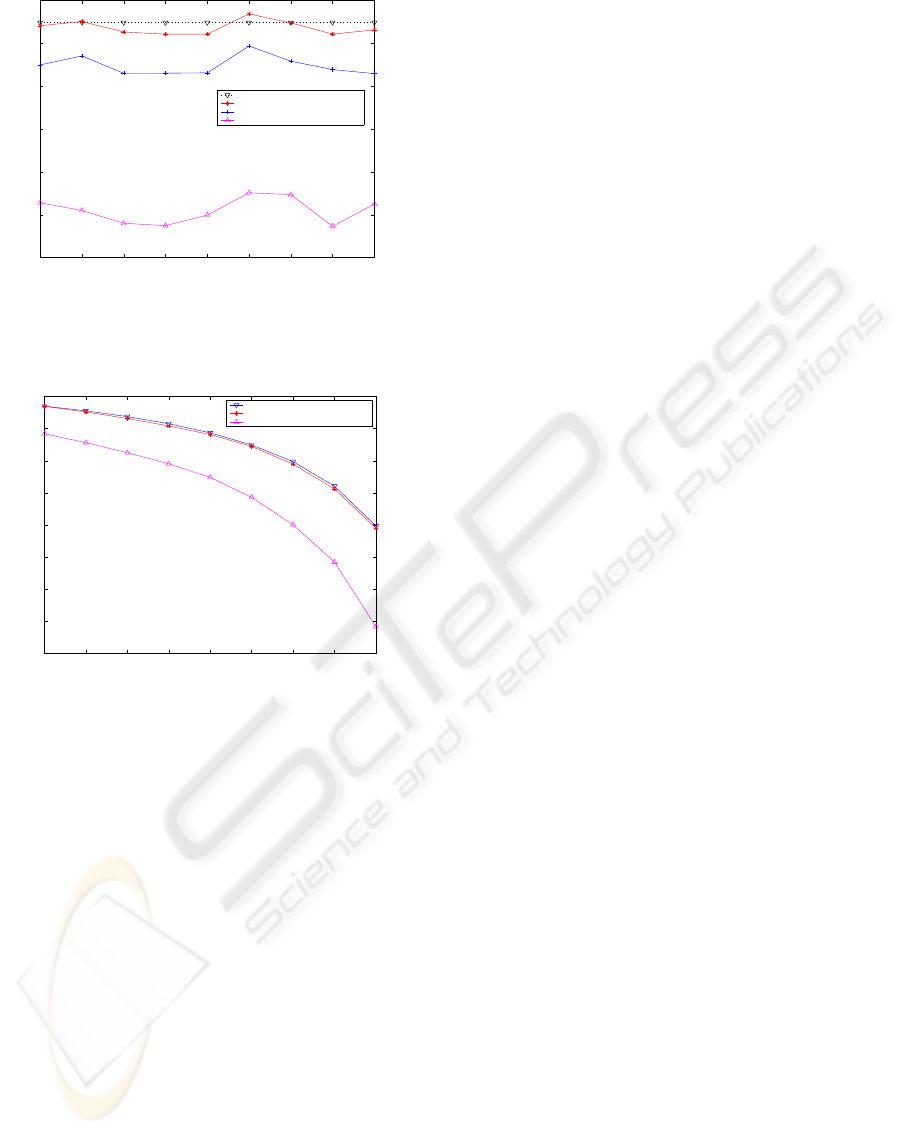
ties are fed into the packet scheduler. Fig. 6 shows
the simulation results, where the x-axis represents the
load factor and the y-axis represents the revenue.
First focusing on our revenue-maximizing ap-
proach, we can see that the revenues obtained under
our optimal weights are extremely close to those of
analytic forms for light and medium loads, and both
decrease along with the load factor. This is as ex-
pected because the increase of the traffic load fed into
the scheduler incurs the increase of the mean delay
and thus the decrease of the obtained revenue. At
heavier loads both curves start to level off sharper
as the penalties start to grow faster. Compared with
our approach, the proportional assignment scheme
achieves less revenues at all traffic loads. And it de-
creases even sharper for heavier load as the penal-
ties incurred under the proportional weights are much
larger than the ones under our optimal weights for the
same load and grow faster.
1 1.5 2 2.5 3 3.5 4 4.5 5
−500
−400
−300
−200
−100
0
100
200
300
Load factor
revenue
Analytic
Simulated under optimal weights
Simulated under proportional weights
Figure 6: Revenue comparison as function of load factor ρ,
for the case, b
1
= 200, k
1
=10000, b
2
= 150, k
2
= 5000,
b
3
= 80, k
3
= 2000.
4.2 The second set of simulations
In the second set of simulations, the same simulations
are made for three different linear pricing functions:
b
1
= 200, k
1
= 5000, for gold class, b
2
= 120, k
2
=
2000, for silver class, and b
3
= 40, k
3
= 500, for
bronze class, to evaluate the performance robustness
of our approach for revenue maximization. Figs. 7
and 8 present the simulation results.
It is observed in Fig. 7 that the revenue obtained
under our optimal weights is the largest and it is also
close to the analytic value by Eq. (15). Since the slope
k
i
of class i in this case is less than the one in the first
set of simulations, the revenue obtained from class i
will decrease more slowly along with the increase of
mean delay in this case, leading to the revenue curves
in Fig. 8 level off smoother for the same load com-
pared with the ones in Fig. 6. Similarly, the largest
revenue is obtained under our optimal weights for all
traffic loads and it is very close to the curve of analytic
maximum revenue. Therefore, it is demonstrated that
our revenue-maximizing approach is effective for any
linear pricing functions.
5 CONCLUSIONS
In this paper, we explored the problem of max-
imizing revenues under multi-class Service-Level-
Agreements. In particular, we considered the opti-
mization problem of maximizing the revenue attained
in a network node under linear pricing scenario. A
revenue-aware scheduling approach was introduced,
which has the closed-form solution to the optimal
weights for revenue maximization derived from rev-
enue target function by Lagrangian optimization ap-
proach. The simulations demonstrated the revenue
maximization ability of our approach.
ICETE 2004 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS
138
100 200 300 400 500 600 700 800 900
230
240
250
260
270
280
290
time (s)
revenue
Analytic
Simulated under optimal weights
Simulated under given weights
Simulated under proportional weights
Figure 7: Revenue comparison as function of time, for the
case, load factor ρ = 1 and b
1
= 200, k
1
=5000, b
2
= 120,
k
2
= 2000, b
3
= 40, k
3
= 500.
1 1.5 2 2.5 3 3.5 4 4.5 5
−100
−50
0
50
100
150
200
250
300
Load factor
revenue
Analytic
Simulated under optimal weights
Simulated under proportional weights
Figure 8: Revenue comparison as function of load factor ρ,
for the case, b
1
= 200, k
1
=5000, b
2
= 120, k
2
= 2000,
b
3
= 40, k
3
= 500.
In the future work, the issue of revenue maximiza-
tion for flat pricing scenario is investigated. More-
over, revenue criterion may be used as an admission
control mechanism. In admission control, the packet
is accepted/rejected by hypothesis test, where revenue
increase/decrease is estimated, when a packet comes.
REFERENCES
Courcoubetis C., Kelly F.P., and Weber R. (2000).
Measurement-based usage charges in communication
networks.
Oper. Res.. Vol.48, No.4, pp. 535-548, 2000.
Golestani S.J. (1994).
A Self-Clocked Fair Queuing Scheme for Broadband
Applications
In Proc. of INFOCOM’94, pp. 636-646, April 1994.
Kelly F.P. (1994).
On tariffs, policing and admission control for multi-
service networks.
Oper. Res. Lett.. Vol.15, pp. 1-9, 1994.
Kelly F.P. (1997).
Charging and rate control for elastic traffic.
European Transaction on Telecommunication, Vol.8,
pp. 33-37, 1997.
Kelly F.P., Maulloo A.K., and Tan D.K.H. (1998).
Rate control for communication networks: Shadow
prices, proportional fairness and stability.
Oper. Res. Soc., Vol.49, pp. 237-252, 1998.
La R.J. and Anantharam V. (2002).
Utility-based Rate Control in the Internet for Elastic
Traffic.
IEEE/ACM Transactions on Networking, Vol.10, Is-
sue: 2, pp. 272-286, April 2002.
MacKie-Mason J.K. and Varian H.R. (1994).
Pricing the Internet, in Public Access to the Internet.
B. Kahin and J. Keller, Eds. Englewood Cliffs, NJ:
Prentice-Hall, 1994.
Parekh A.K. and Gallager R.G. (1993).
A Generalized Processor Sharing Approach to Flow
Control in Integrated Services Networks: The
Single-Node Cases.
IEEE/ACM Transactions On Networking, Vol.1, No.3,
pp. 344-357, June 1993.
Paschalidis I.Ch. and Tsitsiklis J.N. (2000).
Congestion-dependent pricing of network services.
IEEE/ACM Transactions on Networking, Vol.8, pp.
171-184, April 2000.
Paschalidis I.Ch. and Liu Y. (2002).
Pricing in multiservice loss networks: static pricing,
asymptotic optimality and demand
subsitution effects.
IEEE/ACM Transactions on Networking, Vol.10, Is-
sue: 3, pp. 425-438, June 2002.
Stiliadis D. and Varma A. (1995).
Efficient Fair Queuing Algorithm for ATM and Packet
Networks.
Tech. Rep. UCSCCRL-95-59, Dec. 1995.
Stiliadis D. and Varma A. (1996).
Design and Analysis of Frame-based Fair Queuing: A
New Traffic Scheduling Algorithm for
Packet-Switched Networks.
In Proc. of SIGMETRICS’96, pp. 104-115, May 1996.
PACKET SCHEDULING FOR MAXIMIZING REVENUE IN A NETWORK NODE
139
