RELIABILITY ASSESSMENT OF E-COMMERCE APPLICATIONS

V. S. Alagar

Concordia University

Montreal, Quebec, Canada

O. Ormandjieva

Concordia University

Montreal, Quebec, Canada

Keywords:

E-Commerce, reliability prediction, software measurement, Markov model.

Abstract:

The paper discusses a formal approach for specifying time-dependent E-Commerce applications and proposes

a Markov model for reliability prediction. Measures for predicting reliability are calculated from the formal

architectural speciﬁcation and system conﬁguration descriptions. Our methods have been implemented and a

set of sample results obtained from it for a simple system is given.

1 INTRODUCTION

The reliability of a software system is deﬁned in

(IEE, ) as the ability to perform the required function-

ality under stated conditions for speciﬁed period of

time. In this paper the software system under discus-

sion is an E-Commerce system. An E-Commerce can

be viewed as a large and complex distributed system

whose heterogeneous components interact in various

ways to achieve the result of an application. Often,

the performance of an application initiated at a site is

rated as good if the server at that site is robust and

maintains its links to other web objects throughout a

transaction session. Such a rating does give a sub-

jective qualitative assessment, but does not provide a

scientiﬁc quantitative measurement of the reliability

of the site or the system itself. This paper proposes a

rigorous methodology for predicting the reliability of

E-Commerce applications using Markov models con-

structed from a formal model of the E-Commerce ap-

plication.

Many techniques exist to test and statistically an-

alyze traditional software. However, these methods

can not be readily applied to E-Commerce systems.

In a recent paper Kallepalli and Tian (Kallepalli and

Tian, 2001) have surveyed the characteristics of Web

applications and usage and proposed a statistical test-

ing method for Web applications. Their approach

relies on usage and failure information collected in

the log ﬁles. They deﬁne Web failure as the inabil-

ity to correctly deliver information or documents re-

quired by the users. Based on this deﬁnition of failure,

they classify types of failures and provide a method

for testing source or content failures. We comple-

ment and enrich this work by offering a formal time-

constrained model of a simple E-Commerce model.

We propose an early reliability prediction based on

the analysis of the formal architecture model of the

E-Commerce applications using Markov models. A

Markov model dynamically adapts to time-dependent

system conﬁgurations that satisfy the architectural de-

sign (Ormandjieva, 2002). We view the E-Commerce

applications as large Markov systems, in which state

changes within each object of the system occur with

certain probabilities.

Following the work (Papazoglou, 2000), we use

agent paradigm to formally model E-Commerce sys-

tems. Agents are usually qualiﬁed by their goals,

knowledge, beliefs, and intentions. We follow the

property-oriented deﬁnition and classiﬁcation from

(Alagar et al., 2002), and introduce primitive agent

types in modeling an E-Commerce system.

The organization of the rest of the paper is as fol-

lows. A formal model of the E-Commerce is given

in Section 2. Section 3 formally describes the

method of modeling the E-Commerce application as

a Markov system. Section 4 presents the reliability

prediction measures obtained from our implementa-

tion for a simple system. Section 5 concludes the

paper with a discussion on our ongoing research di-

rections.

S. Alagar V. and Ormandjieva O. (2004).

RELIABILITY ASSESSMENT OF E-COMMERCE APPLICATIONS.

In Proceedings of the First International Conference on E-Business and Telecommunication Networks, pages 30-37

DOI: 10.5220/0001399900300037

 SciTePress

2 E-COMMERCE MODEL

In this paper, an agent is a computational entity han-

dling sequences of messages (events) to implement

the expected behavior of an agent as understood in

agent technology (FIP, ; Papazoglou, 2000). Agents

can receive and emit events, generate events inter-

nally, and react to events received from its environ-

ment. Such handling is fully determined by the im-

plementation of the event. Peer-to-peer communica-

tion between agents is enabled by bidirectional con-

nections transmitting events according to a speci-

ﬁed protocol. We refer to (Franklin and Graesser,

1996; Alagar et al., 2002) for agent classiﬁcation,

agent types, agent behaviors, and their conformance

to FIPA agents. We use the notation from (Alagar

et al., 2002) for describing an E-Commerce system.

For illustration, we develop the formal model of an

E-Commerce system consisting of four agent types

User, EBroker, Merchant, and Bank. An instance

of an agent type is an agent. The high-level architec-

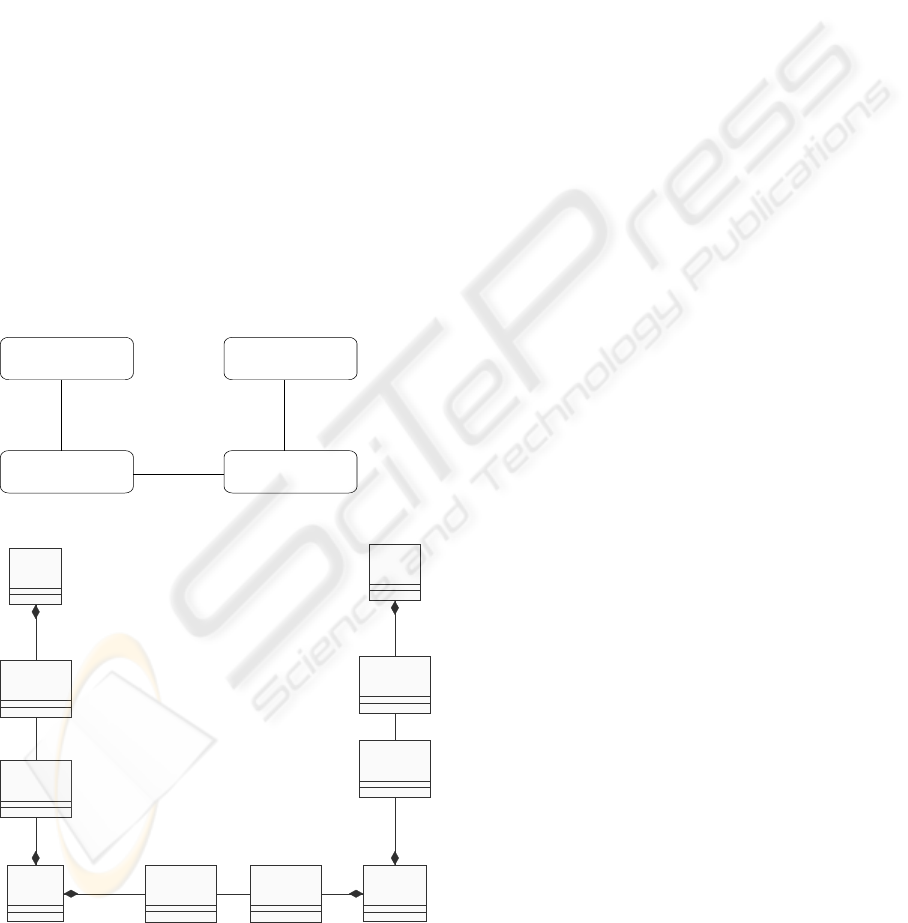
ture shown in Fig. 1(a) captures the allowed connec-

tions between agents in an application.

User

EBroker

Bank

Merchant

(a) Generic E-Commerce Architecture

User

(f rom U ser)

<<GRC>>

(from User)

<<PortType>>

(f rom EBroker)

<<PortType>>

EBroker

(f rom EBroker)

<<GRC>>

(f rom EBroker)

<<PortType>>

(f rom Merchant)

<<PortType>>

Merchant

(f rom Merchant)

<<GRC>>

(f rom Merchant)

<<PortType>>

(from Bank)

<<PortType>>

Bank

(f rom Bank)

<<GRC>>

(b) Agent Types and Port Types

Figure 1: High-Level Architecture Diagrams

2.1 Formal Models

From the architecture shown in Fig. 1(a) we deter-

mine the agent types and port types for each agent

type. A port-type of an agent type [] is an abstrac-

tion of connection point where events are emitted

and received from another agent type. The symbol

@ is used to introduce port types. An agent of the

agent type A[L], where L is the list of port types,

is created by instantiating each port type in L by

a ﬁnite number of ports and assigning the ports to

the agent. Any message deﬁned for a port type can

be received or sent through any port of that type.

For instance, A

, p

: @P ; q

, q

: @Q], and

: @P ; s

, s

: @Q] are two agents of the agent

type A[@P, @Q]. The agent A

has two ports p

and

of type @P , and three ports q

, q

of type @Q.

Both p

and p

can receive or send messages of type

@P ; the ports q

, q

, and q

can receive and send

messages of type @Q. Sometimes the port param-

eters of agents are omitted in our discussion below.

Messages are allowed to have parameters.

An E-Commerce system, consistent with the archi-

tecture in Figure 1(a), consists of a ﬁnite set A of

agents A

, . . . A

, where each A

is an instance of one

of the agent types shown. From the description of the

problem we extract the messages (events) for commu-

nication and partition the set of the messages into co-

hesive subsets, creating port-types. For instance, the

EBroker agent type requires two port types: one for

communication with the User agent and the other for

communication with the Merchant agent. Figure 1(b)

shows a reﬁnement of Figure 1(a) obtained by adding

the port type associations to agent types. The model

is further enriched by including abstract data types to

express abstract computations done by agents.

2.2 Behavior of the System

An agent can handle one external event at a time. We

assume that there is no connection delay, and an agent

emits an event only if the receiver of the event is pre-

pared to accept it. That is, emitting and absorbing an

event is considered as one atomic action. Thus, in a

speciﬁc transaction in the system, the activity of each

agent A on a set of connections C is observed as the

ﬁnite sequence of events which A handles on C in that

session. Notice that the connections C are at the ports

of A and the ports of those agents interacting with it in

that session. The trace of A on C is the set of all com-

putation paths in the state machine description of A.

The set of all traces of A is referred to as the behav-

ior of A. Fig. 2 and Fig. 3 show the state machines

for the agents in our E-Commerce system. To illus-

trate the usefulness of time constraints we have spec-

iﬁed time constraints for EBroker actions. In general

RELIABILITY ASSESSMENT OF E-COMMERCE APPLICATIONS

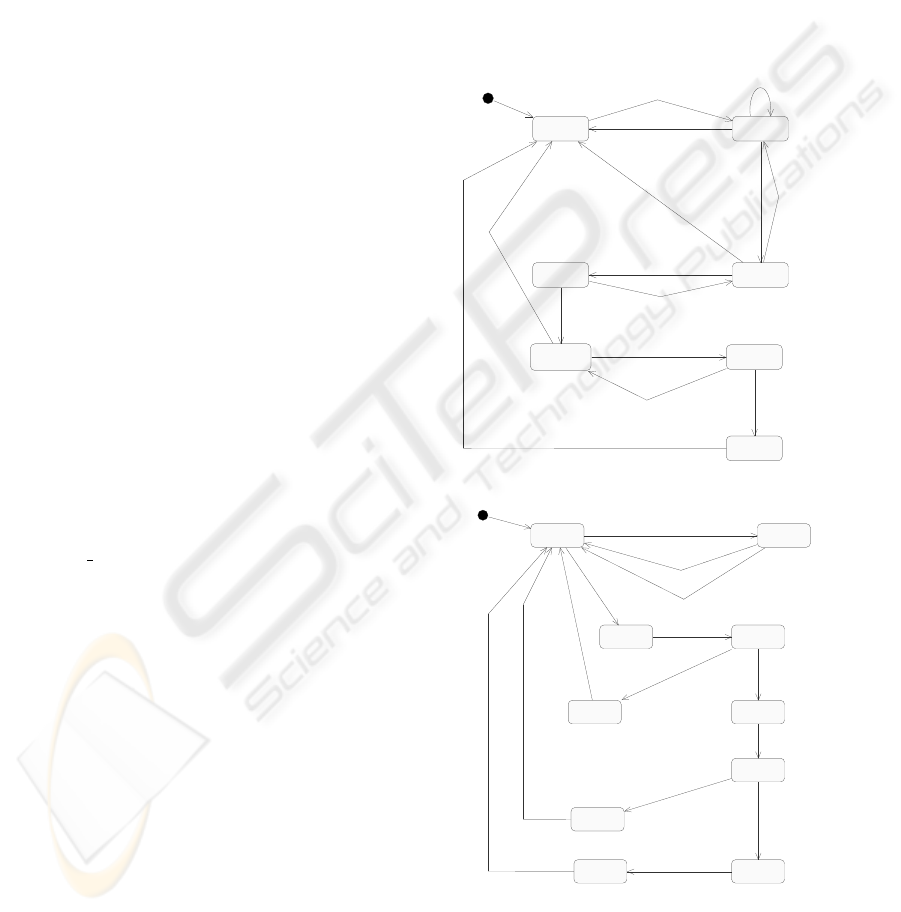
Merchant and Bank agents should also respect time-

liness, and appropriate time constraints can be intro-

duced in their speciﬁcations.

A successful transaction is conducted by the agents

in the following manner. The E-Commerce system

is initiated with the message BrowseAdd from a user

to the broker. Both User and EBroker agents syn-

chronize on this event: the agent User goes to active

state, the agent EBroker goes to the state getProd-

uct. The other agents do not change their states. The

agent EBroker sends the message GetProductInfo to

the Merchant agent within 2 units of time from the

instant of receiving the message BrowseAdd, and they

both simultaneously change their states to waitProd-

uct, and product respectively. The Merchant agent

responds to the agent EBroker with the message Pro-

ductInfo which cause them to simultaneously change

their states to idle, and browseSucceed. Within 2 units

of time of receiving the webpage from the merchant

the EBroker communicates to the User agent with

the message page, causing them to simulataneously

change their states to idle and readPage. This com-

pletes the ﬁrst phase of a successful user interaction,

where the user has received a web page for browsing.

The user may decide to exit or may enter the next

phase of transaction by initiating the message Item to

the agent EBroker. In the later case, they synchro-

nize and change their states to wait and startNego-

tiation. The user continues to wait until the EBro-

ker agent completes a sequence of internal compu-

tations triggered by the internal events hAddStatistic,

TotalQuantity, GetMinPrice, GetRiskBalance, Calcu-

lateAcceptablePrice i. All brokers share a table of

information on user requests. Each entry in the ta-

ble is a tuple containing userid, merchantid, produc-

tid, quantity requested and priceofferred. Based on

this table of information and a formula for risk-proﬁt

analysis, the broker determines a price of a product.

We have used abstract data types to specify tables and

databases within agent types.

After completing the risk-proﬁt analysis, the offer

made by the user is either accepted or rejected by

the agent EBroker. The decision to accept or reject

the price offer is communicated to the user within the

time interval [t+5, t+8], where t is the time at which

the message item was received by the broker. For a

successful transaction, the message Conﬁrmed is ex-

changed between the User and EBroker agents, caus-

ing their simultaneous transitions to the states conﬁr-

mation and idle. This completes the second phase

of successful transaction. At this instance, the User

agent is in state conﬁrmation and the other agents are

in idle states.

The user can exit from the system without making

a purchase at this stage. The product is purchased

by the user and the invoice is received in the next

and ﬁnal phase of the transaction. The message Pur-

chase is sent by the agent User to the agent EBroker,

and the User agent goes to waitinvoice state where it

waits until receiving the message ReceiveInvoice from

the agent EBroker. The EBroker agent communi-

cates with Merchant agent through the message Gen-

erateInvoice and they simulataneously change their

states to askMerchant and getInvoice. At this instant,

the User is in state waitinvoice, the agent EBroker is

in state askMerchant, the agent Merchant is in state

getinvoice, and the agent Bank is in state idle. The

states of User and EBroker do not change until the

agents Merchant and Bank collaborate to produce

the invoice.

idle active

wait readPage

confirmation

waitInvoice

viewInvoice

BrowseAdd

Exit

Item

Exit

Purchase

ReceiveInvoice

Page

AddressError

NotConfirmed

Confirm ed

Exit

InvoiceFailed

(a) Statechart Diagram for User

idle product

getInvoice merchantA

accFind

startCharg

GetProductInfo

ProductNotFind

ProductInfo

GenerateInvoice

GetMerchantAcc

SucceedAtMerchantAcc

Charge

accNotFind

FailedAtMerchantAcc

Unsuccessful

succeed

failure

invoice

SucceedAtCharge

FailedAtCharge

AddInvoice

Unsuccessful

Successful

(b) Statechart Diagram for Merchant

Figure 2: Behavior Descriptions - 1

To produce the invoice, the agent Merchant sends

the message GetMerchantAcc to the agent Bank, re-

ICETE 2004 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

idle search

GetMerchantAcc

chargeAcc

findingAccaccNotFou

accFound

chargedFro

mCust

validCharge

GetCustomerAccBalance

AccNotFind

AccFind

DepositToMerchant

SucceedAtCharge

wait

Charge

FailedAtMerchantAcc

SucceedAtMerchantAcc

FailedAtCharge

WithdrawFromCustom er

FailedAtCharge

(a) Statechart Diagram for Bank

idle

getProduct

waitProduct

GetProductInfo[ true && true

&& TCvar1 <= 2 ]

browseFail

browseSuc

ceed

ProductNotFind[ true && true &&

true ] / true && TCvar2=0

AddressError[ true &&

true && TCvar2<=2 ]

ProductInfo[ true && true

&& true ] / true &&

TCvar3=0

Page[ true && true

&& TCvar3<=2 ]

startNegoti

ation

waitOthers

quantity

minPrice

riskFactor

AddStatistic[ true && true && true

] / sl’ = insert(s, sl)&& TCvar4 = 0

TotalQuantity[ true && true

&& TCvar4>=3 & TCvar4<=6

] / tq’ = totalQuantity(sl)

GetMinPrice / minprice =

getMinPrice(mid, pid, tq, rul)

GetRiskBalance / rf’ =

getRiskBalance(q/tq, ril)

acceptable

Price

CalculateAcceptablePrice / ap’ =

minprice * rf

negoResult

DeleteStatistic / sl’ = delete(s, sl)

BrowseAdd[ true &&

true && true ] / true &&

TCvar1=0

Item[ true && true && true ] / s’ =

create(uid, mid, pid, q, n) & uid1’ =

uid & mid1’=mid & pid1’ = pid & q1’ =

q & n1’ = n && TCvar5=0 & TCvar6 = 0

startInvoice

Purchase

askMercha

succeed

failure

GenerateInvoice

InvoiceFailed[ true && true

&& TCvar8 <= 2 ]

Unsuccessful[ true &&

true && true ] / true

&& TCvar8=0

Successful[ true && true &&

true ] / true && TCvar7 = 0

commissio

AddCommission / cl’ =

insert(create(mid, invid,

amount), cl)

ReceiveInvoice[

true && true &&

TCvar7<=2 ]

Confirmed[ ap <= n1

&& true && TCvar5

>= 5 & TCvar5 <= 8

]

NotConfirmed[ ap

> n1 && true &&

TCvar6 >= 5 &

TCvar6 <= 8 ]

(b) Statechart Diagram for EBroker

Figure 3: Behavior Descriptions - 2

ceives back the reply SucceedMerchantAcc, and then

responds through the message Charge. At the end

of this sequence of message exchanges, they reach

the states startCharge and chargeAcc. The Merchant

agent waits in state startCharge until the Bank agent

completes a sequence of internal computations and

sends the message SucceedAtCharge to it. Upon re-

ceiving this message, the Bank agent goes to idle

state, the Merchant agent goes to succeed state. Af-

ter completing the internal computation to record the

invoice, the Merchant agent communicates to EBro-

ker through the message Successful and their states to

idle, and succeed. At this instance, the agents Bank

and Merchant are in their idle states, the agent EBro-

ker is in state succeed, and the agent User is in state

waitinvoice. The agent EBroker records the commis-

sion earned in this transaction within 2 time units of

receiving the message ReceiveInvoice and sends the

invoice to the User. Having sent the invoice, the

agent EBroker goes to its idle state. The agent User

executes the internal message Exit and goes into its

idle state.

Figure 4 shows an E-commerce system conﬁgured

with three users, one E-broker, two merchants and

three banks. Each instance of User type models a

user with one port of type @A to communicate with

an agent of EBroker type. The E-broker agent in the

subsystem is an instance of EBroker agent type hav-

ing three ports of type @U, one port for each user; the

two ports of type @M are for communication with

the merchants in the system. Each merchant agent

in the system is an instance of Merchant agent type

with a port of type @G for communicating with the

broker agent, and three ports of type @B to commu-

nicate with the banks in the system. The agents are

linked through connectors at their respective compat-

ible ports for communication. For instance, the port

@A1 of user U 1 is linked to the port @U1 of the E-

broker E1. That link is not shared by any other agent.

Consequently, the architecture speciﬁcation ensures

trust in communications.

The following section introduces a rigorous

methodology for predicting the reliability of E-

Commerce applications using Markov models con-

structed from a formal model of the E-Commerce ap-

plication.

3 MARKOV MODELS

Markov models are one of the most powerful tools

available to engineers and scientists for analyzing

complex systems. The basic concepts are explained

below.

3.1 Markov Models: Basic Concepts

Analysis of Markov models yield results for both the

time-dependent evolution of the system and the steady

state properties of the system. The Markov property

states that given the current state of the system, the

future evolution of the system is independent of its

history.

The Markov model of an E-Commerce component

may be represented by a state diagram. The states

represent the stages in the E-Commerce component

that are observable to the users, and the transitions be-

tween states have assigned probabilities. An algebraic

representation of a Markov model is a matrix, called

transition matrix, in which the rows and columns cor-

respond to the states, and the entry p

in the i-th row,

j-th column is the transition probability for being in

state j at the stage following state i. We use tran-

sition matrix representation in reliability calculation

algorithms.

RELIABILITY ASSESSMENT OF E-COMMERCE APPLICATIONS

U1 :

User

U2 :

User

U3 :

User

@A1 :

@A2 :

@A3 :

@U1 :

@U2 :

@U3 :

E1 :

EBroker

@G1 :

@G2 :

M1 :

Merchant

M2 :

Merchant

@B1 :

@B2 :

@B3 :

B1 :

Bank

B2 :

Bank

B3 :

Bank

@M1 :

@M2 :

@M3 :

@B4 :

@B5 :

@B6 :

@M4 :

@M5 :

@M6 :

@C1 :

@C2 :

Figure 4: Subsystem Architecture

3.2 Discussion

Initial transition probabilities, obtained from various

sources including log ﬁles and other subjective opin-

ions of experts can not be used for predicting the re-

liability of the system. We contend that the reliabil-

ity should be calculated from the steady state of the

Markov system. A steady state or equilibrium state is

one in which the probability of being in a state before

and after transitions is the same as time progresses.

Computing the steady state vector for the transition

matrix of a large system is hard. However, as in our

approach, when the system is modularly constructed

it seems possible to partition the system into smaller

components, which might reduce the complexity of

computing steady state vectors.

3.3 Algorithm

We construct the Markov model of a E-Commerce

system in three steps. In the ﬁrst step we construct

the Markov models for E-Commerce objects. In the

second step we construct the Markov models for every

pair of interacting objects in the system conﬁguration

speciﬁcation. Finally in the third step we construct

the Markov model for the fully conﬁgured system.

3.3.1 Step 1: Markov Models for Objects

We associate with each E-Commerce object in the

architecture another ﬁnite state machine, called its

Markov model. The states in the Markov model of

an object are the states of the object in its state ma-

chine description. A transition between two states in

the Markov model is deﬁned only if there exists at

least one transition between those states in its state

machine. In the absence of statistical information

gathered by experts on the usage and failure, we will

assume that all the external events have equal proba-

bility in each state. For the transition from state i to

state j in the Markov model, a ﬁxed probability p

it going into state j at the next time step is calculated

as follows:

1. The initial probabilities for all the transitions in the

state machine of the reactive object are calculated.

The algorithm for calculating such probabilities for

a state is based on the following assumptions: 1)

all external events that can happen at the state have

the same probability; 2) all internal events that can

happen at the state have the same probability, and

(3) these are in general different.

2. In case there is more than one transition

, . . . , l

} of the same type (shared/internal) from

state

to state

, then the above mentioned transi-

tions are substituted by one whose probability is

P = 1 − (1 − P{l

}) × . . . (1 − P {l

})

3. The probabilities of all the transitions for a state

have to sum to 1.

3.3.2 Step 2: Markov Model for Object Pairs

The interaction between two objects is due to shared

events. We compute the state machine for an interact-

ing pair of objects and compute the Markov model

with transition probabilities from the transitions at

each state of the product machine.

Algorithm for Transition Matrix for the

Synchronous Product Machine

Let E

and E

be the sets of internal events in the

statecharts P and Q of interacting objects, and F de-

note the set of shared events. Let M

and M

be the

transition matrices for P and Q. Let R be the syn-

chronized product machine of P and Q. Algorithm

SPM computes the transition matrix M of R by ﬁrst

computing the synchronous product machine R, and

next determining the transition probabilities for tran-

sitions in each state of R. If all the transitions in a

state are labeled by internal events or if all of them

are labeled by shared events the probabilities are ob-

tained by normalizing the probabilities in their respec-

tive machines. However, if both internal events and

ICETE 2004 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

shared events occur at the state, the probabilities for

the shared events are calculated ﬁrst, and the remain-

ing measure is distributed to transitions labeled by in-

ternal events.

Algorithm SPM

Step 1. p = 1; // row sum

Step 2. x

= {e| e is a shared event occurring at

state i (P) and at state j (Q) }

= {e| e is an internal event occurring at state i

(P )} ∪ {e| e is an internal event occurring at state

j (Q) }

Step 3. If x

6= ∅ // calculate probabilities for tran-

sitions due to shared events

then NF = 0 (Normalization Factor); set

= ∅;

Step 3.1 For each event e ∈ x

ﬁnd the (set of)

states i

(P ) and j

(Q) such that i

→ i

, j

→ j

Step 3.2 y = y ∪ {i

, j

}, if {i

, j

} /∈ y

Step 3.3 NF = N F + M

[i, i

] × M

[j, j

]

Step 3.4 M[(i, i

), (j, j

)] = M

[i, i

]×M

[j, j

]

Step 3.5 set

= set

∪ (j, j

)

Step 4. If x

6= ∅ // calculate probabilities for tran-

sitions due to internal events

then NF

= 0 (Normalization Factor); set

= ∅;

Step 4.1 For each event e ∈ x

, if e ∈ M

then

ﬁnd the state i

) such that i

→ i

;

y = y ∪ {i

,j} if {i

,j} /∈ y;

M[(i, j)(i

, j)] = M

[i, i

]; N F

= NF

M[(i, j)(i

, j)];

set

= set

∪ (i, i

)

else

ﬁnd the state j

) such that j

→ j

;

y = y ∪ {i, j

} if {i, j

} /∈ y;

M[(i, j)(i, j

)] = M

[j, j

]; NF

= NF

M[(i, j)(i, j

)];

set

= set

∪ (j, j

)

Step 5. If x

= ∅ ∧ x

= ∅, the (i, j) row is deleted

from M

Step 6.If x

= ∅ ∧ x

6= ∅

For each (i

, j

) ∈ set

M[(i, j), (i

, j

)] =

M[(i, j), (i

, j

)]

Step 7. If x

6= ∅ ∧ x

= ∅

For each (i

, j

) ∈ set

M[(i, j), (i

, j

)] =

M[(i, j), (i

, j

)]

Step 8. If x

6= ∅ ∧ x

6= ∅ do

For each (i

, j

) ∈ set

M[(i, j), (i

, j

)] =

(1 − NF ) × M[(i, j), (i

, j

)]

Step 9. Fill in the matrix M with 0 where there are

no entries.

3.3.3 Step 3: Markov Model for a System

A system conﬁguration, when partitioned into slices

based on synchronization criteria, produces two types

of subsystem components: (1) linear conﬁguration,

and (2) non-linear conﬁguration. As an illustration, a

simple system in which one user is interacting with

a browser to access information, as shown in Fig-

ure 5(a) is linear, whereas the system in which users

join the system at different times, as shown in Fig-

ure 5(b) is non-linear.

Case 1: Linear System

In a linear system, objects synchronize in the past.

If o

, . . . , o

are objects in the linear system and

, . . . , M

are respectively their transition matri-

ces, then the transition matrix M of the linear system

is computed as follows:

1. Compute M = M

⊗M

(Apply Algorithm SPM)

2. for j = 3 to n compute M = M ⊗ M

(Apply

Algorithm)

Case 2: Non-linear System

In a non-linear system, as in Figure 5(b), several ob-

jects interact with an object. These interactions may

be initiated at different times. The synchronous prod-

uct machine dynamically changes as and when ob-

jects join or leave the system, and hence the transition

probability matrices also change, and should be re-

computed. We explain the computation procedure for

Figure 5(b). For simplicity of discussion we assume

that users join the system one at a time, but don’t leave

the system. Let 0, k

, k

, . . . , k

n−1

be the intervals of

successive arrivals of users. That is, for j > 1 the

j-th user joins the system k

j−1

(> 0) time units after

j − 1-st user joined the system. Let M

be the transi-

tion matrix of the Markov model for the linear system

computed at time step k. The transition matrix for

(n)

, n ≥ 2, users interacting with one browser and

one server object is calculated as follows:

RELIABILITY ASSESSMENT OF E-COMMERCE APPLICATIONS

User Server

Browser

Ini

synchronize

(a) Linear Architecture

User User UserUser

1 2 3 n

Server

Browser

(b) Non-Linear Architecture

Figure 5: Linear and Non-Linear Models

(2)

= M

(3)

= [M

(2)

]

(j)

= [M

(j−1)

]

j−1

, 2 ≤ j ≤ n

In the above calculation, the symbol

denotes the

direct product operator for matrices. The justiﬁcation

for direct product computation is based on the obser-

vations:

• the event received by the system from a new User

object can come only when the system is in any one

of its states in which it can be accepted,

• the incoming event is not time-constrained with re-

spect to the Markov model of the system. that

is M

for the new interaction is independent of

(j−1)

]

j−1

, and

• when a new object joins the system the size of the

new Markov matrix increases m-fold, where m is

the size of the Markov matrix of the new object.

For the non-linear system in Figure 5(b), assume that

four users join the system,one at a time, at times 0,

2, 4, 5. So, k

= 2; k

= 1. The transition

matrix of the system at different time points are shown

below:

At time 0 or 1: (1 user): M

At time 2: (2 users): M

(2)

= M

At time 4: (3 users): M

(3)

= [M

(2)

]

At time 5: (4 users): M

(4)

= [M

(3)

]

Let us consider the general case when r > 1 users si-

multaneously join the system, say when there are j−1

users in the system. It is easy to see that the transition

matrix for the new conﬁguration with r + j − 1 users

is M

(r+j−1)

= [M

(j−1)

]

j−1

(r)

, where M

(r)

is the direct product M

. . . M

, taken r

times. When r users leave the system, the transition

matrix is computed as follows: Let there be j(≥ 2)

users in the system when r(1 < r ≤ j) users leave.

If r = j, then the transition matrix is not deﬁned. If

r < j, there are j − r users left in the system. If d

is the interval of time that elapsed between the latest

time when there were j − r users in the system and

the current instant, then the new transition probability

matrix is [M

(j−r)

]

. The rationale is that the transi-

tion probability matrix M

(j−r)

for j − r users have

evolved over d time steps.

For the E-Commerce system shown in Figure 4

the Markov matrix can be computed using the above

method. The details are left to the reader.

4 RELIABILITY MEASURES

We deﬁne the reliability prediction for a system con-

ﬁguration composed from k objects as the level of cer-

tainty quantiﬁed by the source excess − entropy:

Reliability(Subsystem) =

i=1

− H

where H = −

log p

is a level of

uncertainty of the Markov system corresponding to a

subsystem; v

is a steady state distribution vector for

the corresponding Markov system and the p

values

are the transition probabilities. H

is a level of un-

certainty in a Markov system corresponding to a reac-

tive object. For a transition matrix P the steady state

distribution vector v satisﬁes the property vP = v.

The level of uncertainty H is related exponentially to

the number of paths that are ”statistically typical” of

the Markov system. Thus, higher entropy value im-

plies that more sequences must be generated in order

to accurately describe the asymptotic behavior of the

Markov system.

The reliability prediction for a system is deﬁned as

the least reliability measure value among its m sub-

systems:

Reliability(System) =

min{Reliability(Subsystem

)}

We chose the minimum value due to the safety-critical

character of the real-time reactive systems. Higher

value of reliability measure implies less uncertainty

present in the model, and thus higher level of software

reliability.

The Markov model of a conﬁgured system changes

when the system undergoes change. The calcula-

tion of the Markov matrix for the reconﬁgured sys-

tem would allow to compare the systems based on re-

liability prediction. If the system conﬁguration C

j−1

ICETE 2004 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

changes to the conﬁguration C

, we need to calculate

the reliability of the conﬁguration C

and compare it

with the reliability of the conﬁguration C

j−1

Reliability(C

j−1

) = min{Reliability(S

)}

where S

is a subsystem of C

j−1

, and

Reliability(C

) = min{Reliability(S

)}

where S

is a subsystem of C

. If Reliability(C

) ≥

Reliability(C

j−1

), then the uncertainty present in

the reconﬁgured system is less than the uncer-

tainty that existed in the current system. The

reliability measurement will allow the reconﬁg-

ured system to be deployed. However, if

Reliability(C

) < Reliability(C

j−1

), then there is

more uncertainty present in the reconﬁguration. This

would suggest to determine the subsystem(s) of C

that are responsible for lowering the overall reliabil-

ity.

5 CONCLUSIONS AND

RESEARCH DIRECTIONS

The goal of this paper is to show that a rigorous ap-

proach to reliability prediction of E-Commerce sys-

tems is possible, when we construct a formal model

of it. The E-Commerce model introduced in this pa-

per is simple, yet a realistic model which is complex

enough to serve as a test bed for experimentation. In

a practical setting, the number of E-Commerce com-

ponents and their interactions will be much larger.

There are also other factors such as resource con-

straints, load factor, and communication complexity.

From a reliability point of view, we require a good

formal model which takes these factors into account.

In the formal model proposed in this paper the load

factor and communication delays can be brought in

as synchronization constraints, and resources can be

modeled within each class and timing constraints may

be imposed on database transactions. Calculation of

transition probabilities for large evolving conﬁgura-

tions involves multiplying fairly large matrices. The

density of the transition probability matrix of a sys-

tem depends on the number of transitions in the prod-

uct matrix, which due to synchronization constraints,

might be sparse. The sparsity of the matrix and the

availability of very fast powering and multiplication

algorithms for matrices may be used to speed up reli-

ability calculation for changing conﬁgurations.

Our research is based on the premise that E-

Commerce systems should be analyzed for several

improperties before deployed for public use. Secu-

rity and reliability are two important properties. Re-

liability promotes trust and security preserves trust.

We have a full implementation of the reliability cal-

culation based on the methods discussed in this pa-

per. One of our ongoing efforts is centered on for-

malizing security policies and integrating them with a

component-based implementation of our model.

REFERENCES

In IEEE Standard Glossary of Software Engineering Termi-

nology. IEEE 610.12.1990.

In FIPA Communicative Acts Library. FIPA Speciﬁcation

Repository (2001). Foundation for Intelligent Physical

Agents, G.

Alagar, V., Holliday, J., Thiagarajan, P., and Zhou, B.

(2002). Agent types and their formal descriptions. In

Technical Report, Department of Computer Engineer-

ing, Santa Clara University, Santa Clara, California,

U.S.A.

Franklin, S. and Graesser, A. (1996). Is it an agent or

a program?: A taxonomy for autonomous agents.

In Proceedings of the Third International Workshop

on Agent Theories, Architectures, and Languages.

Springer-Verlag.

Kallepalli, C. and Tian, J. (Nov. 2001). Measuring and

modeling usage and reliability for statistical web test-

ing. In IEEE Transactions on Software Engineering,

(Vol.27, No.11), pp.1023–1036. IEEE.

Ormandjieva, O. (2002). Deriving new measurements for

real-time reactive systems. In Ph.D. thesis, Concordia

University, Montreal, Canada.

Papazoglou, M. P. (April 2000). Agent-oriented technology

in support of e-business. In Communications of the

ACM, Vol.44. No.4.

RELIABILITY ASSESSMENT OF E-COMMERCE APPLICATIONS