
BVA
+
- A BIT VECTORS ALGORITHM FOR ACCELERATING
QUERIES IN MULTILEVEL SECURE DATABASES
Ramzi A. Haraty, Arda Zeitunlian
Lebanese American University, P.O. Box 13-5053 Chouran, Beirut, Lebanon 1102 2801
Keywords: Bit vectors, query accelerations, and multilevel security
Abstract: Much research has been done in the area of multilevel database systems, especially in the security area and
accelerating queries. In this paper, we present BVA
+
, which is based on bit vectors to accelerate queries in
multilevel secure database systems. As its predecessor (BVA), the BVA
+
algorithm follows the classic Sea
View Model, but it recovers query output from single-level relations in a faster and more space-efficient
manner than the previous works performed on this subject. In addition, the BVA
+
algorithm does not
produce spurious or extra tuples, which have always been a major problem in the area of multilevel secure
database systems.
1 INTRODUCTION
Much research has been done in the area of
multilevel database systems, especially in the
security area and accelerating queries (Jajodia, 1991;
Sandhu, 1994; Rahal, 2003). One of the earliest
attempts to model multilevel relations was the Sea
View Model (Lunt, 1990), which represented two
algorithms. 1) The decomposition algorithm, which
partitioned multilevel relations into single-level
relations and stored each single-level relation
separately, and 2) The recovery algorithm, which
regenerated a multilevel relation from the set of
single-level relations. Since multilevel queries
would result in applying repeated joins to single-
level relations, in addition to the problem of spurious
tuples, the Sea View model performed inefficiently.
The later works, the DVA algorithm (Perrizo, 1993)
and the BVA algorithm (Haraty, 2003), following
the Sea View Model, propose faster recovery
algorithms and are more space efficient.
In this paper, we follow the widely accepted
m
odel for enforcing mandatory access control
policies developed by Bell and LaPadula (Bell,
1976) and describe a fast, space efficient, and secure
technique for accelerating queries that take place
among various single-level relations in a multilevel
secure database system. We show that we achieve a
significant performance improvement over already
published work and produce output data that is
consistent.
The rest of this paper is organized as follows:
Sectio
n 2 provides a brief explanation of multilevel
relations and a description of the concept of
polyinstantiation. Section 3, presents related work.
Section 4 presents the BVA
+
algorithm and its data
structures. Finally, the conclusion is given in section
5.
2 MULTILEVEL RELATIONS
AND POLYINSTATIATION
A multilevel relation (see figure 1) is a relation of
the form R (A1, C1, ..., An, Cn, TC) where Ai is an
attribute and Ci is its classification (or sensitivity
level). TC is the classification of the tuple. Ci
belongs to the domain of classifications for data
items. We denote A1 to be the apparent key of R.
The concept of a key is a little bit different in
multilevel relations because keys can be duplicated;
this is why we refer to them as apparent keys instead
of just keys. The reason behind this duplication of
keys is polyinstantiation.
495
A. Haraty R. and Zeitunlian A. (2004).
BVA+ - A BIT VECTORS ALGORITHM FOR ACCELERATING QUERIES IN MULTILEVEL SECURE DATABASES.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 495-499
DOI: 10.5220/0002593504950499
Copyright
c
SciTePress

Figure 1: A multilevel relation.
A polyinstantiated tuple is a tuple that exists
more than once in a relation with the same apparent
key, but with some other attribute values being
changed. This is due to the fact that different
subjects are authorized to update or view different
data. For example, suppose that a subject X with
clearance C (Confidential) is attempting to write a
new value to a data item Y with sensitivity S
(Secret). The old value in item Y is not viewable by
subject X but the new value written into Y by X is
viewable (it has X's clearance level which is C). To
preserve the old value of Y, a new tuple is inserted
into the relation with same apparent key (and same
attribute values except for Y in this case). Now X can
view the new value inserted into Y and Secret and
Top Secret users will view the two values (the old
value with sensitivity S and the new value with
sensitivity C).
3 RELATED WORK
There are many algorithms built for maintaining and
recovering multilevel relations from single-level
relations. Perhaps the most important of which are
the Sea View model, the DVA algorithm, and the
BVA algorithm.
3.1 The Sea View Model
The Sea View model consists of two algorithms: a
decomposition algorithm and a recovery algorithm.
The decomposition algorithm divides a multilevel
relation R into a set of single level relations. For
every query, an output multilevel relation is
reconstructed from the single-level relations using
the recovery algorithm. Unfortunately, the recovery
algorithm of the Sea View model suffers from the
following: a) Creation of spurious tuples in the
output (due to polyinstantiation), b) Space
inefficiency due to temporary tables, and c) Time
inefficiency due to unions and joins, which are two
of the most expensive database operations.
Spaceship
Name Objective (obj)
Destination
(des)
TC
SHU-1 U Explore U Uranus U
U
APL-9 U Mine U Neptune C
C
RDA-6 U Scientific C Pluto C
C
CLB-2 C Explore C Neptune C
C
CLB-2 C Spy S NULL S
S
3.2 The DVA Algorithm
DVA is an algorithm motivated by the recovery
algorithm of the Sea View Model based on domain
vector accelerators, DVAs, to accelerate the
recovery of multilevel relations from single-level
relations. DVAs accelerate joins between relations
and thus lead to reducing the response time of
queries requiring many joins. The DVA algorithm
solves the problems of the Sea View Model recovery
algorithm; it does not create spurious tuples in the
output table and is relatively space and time
efficient. It shows improvement especially in
environments where queries involve selections on
some (one or more) attributes of the multilevel
relations. In spite of these facts, this algorithm uses a
lot of temporary data structures, some of which can
be omitted to improve the algorithm’s space
efficiency without negatively affecting its overall
performance or its functionality.
3.3 The BVA Algorithm
The Bit Vector Algorithm (BVA) is an algorithm
also motivated by the recovery algorithm of the Sea
View Model to accelerate the recovery of multilevel
relations from single-level relations. BVA solves the
problems of the Sea View Model recovery algorithm
and space and time requirements of the DVA
algorithm; it does not create spurious tuples in the
output table and is space and time efficient. In spite
of these facts, it takes much calculation in finding
the temporary storage used to create the output table,
and may produce inconsistent data.
4 THE BVA
+
ALGORITHM
In this algorithm, we assume that a multilevel
relation is decomposed into single level relations
using the decomposition algorithm of the Sea View
model. The BVA
+
algorithm will be applied to
recover the multilevel relation from those single
level relations. Suppose, we have the multilevel
relation in figure 1. This multilevel relation is based
on single-level relations as shown in figure 2.
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
496
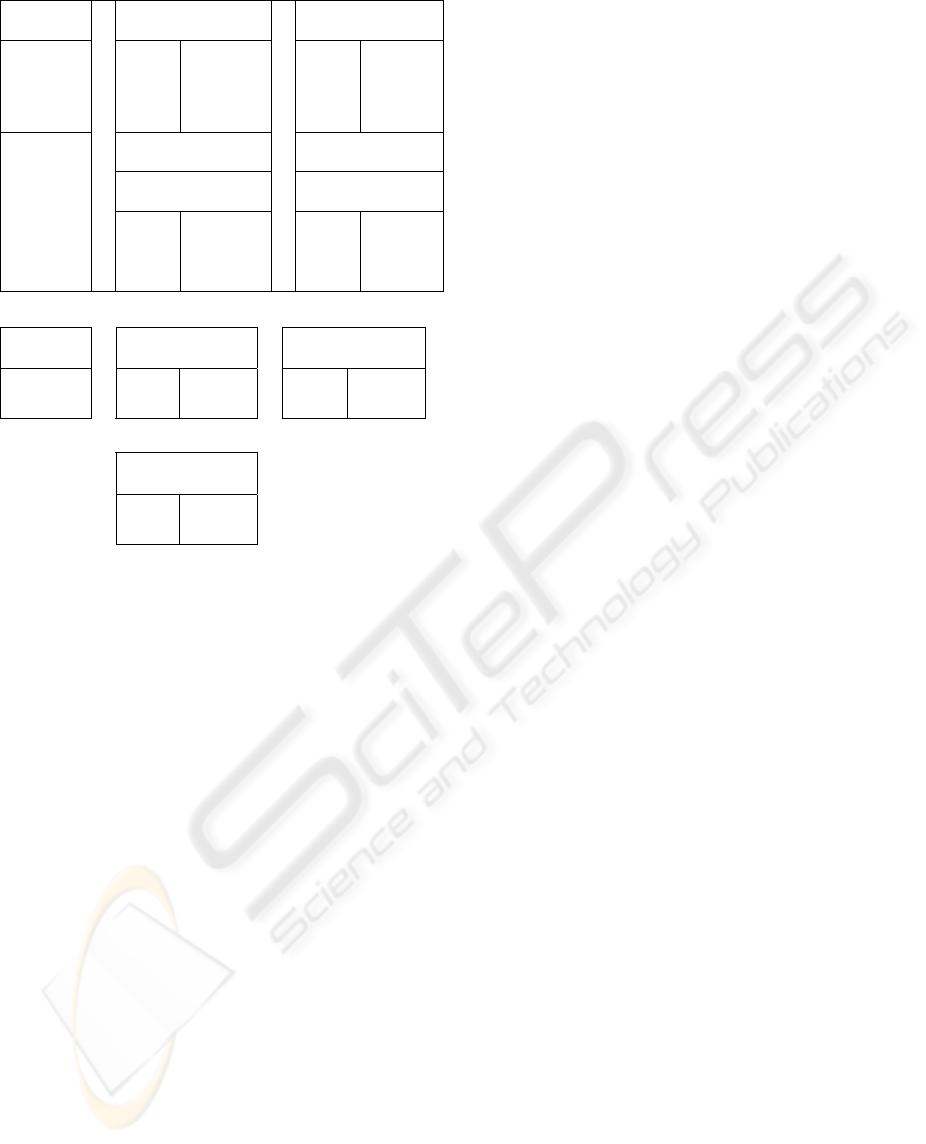
Rname,u Robj,u,u Rdes,u,u
SHU-1
APL-9
RDA-6
SHU-
1
APL-9
Explore
Mine
SHU-
1
Uranus
Robj,u,u Rdes,u,c
RDA-
6
Scientific
APL-9
RDA-
6
Neptune
Pluto
Rname,c Robj,c,c Rdes,c,c
CLB-2 CLB-
2
Explore CLB-
2
Neptune
Robj,c,s
CLB-
2
Spy
Figure 2: The decomposed single-level relations.
All relations containing only the key - i.e.,
Rname,u (base single level relation containing all
keys at classification level U) and Rname,c - are
referred to as base relations. Suppose we want to
recover the output of the query “Select name, obj,
des from R where des <> Saturn”. The following is
a description of the steps of the BVA+ associated
with examples from the above the relation (Ai
denotes any attribute and A1 denotes the apparent
key).
1. For every relation RAi,x,y (single level relation
containing all entries form multilevel relation
having keys at classification level x and Ai
attribute values at classification level y), excluding
base relations, create a bit vector BV.RAi,x,y
denoting the presence or absence of the keys at
level x. BV.RAi,x,y should have the same number
entries as the number keys at level x (can be found
in relation Rkey,x).
Keys at level u = {SHU-1, APL-9, RDA-6}
Keys at level c = {CLB-2}
BV.Robj,u,u = 110
BV.Robj,u,c = 001
BV.Robj,c,c = 1
BV.Robj,c,s = 1
BV.Rdes,u,u = 100
BV.Rdes,u,c = 011
BV.Rdes,c
,c = 1
2. For every RAi,x,y excluding base relations create a
Mapping Vector Index, MVI.RAi,x,y, mapping the
position of the keys in RAi,x,y to the position of
the keys in RA1,x. The entries in the MVIs are of
the form (pib, pit) where pib, Position In Base
relation, is the position of the key in the base
relation; and pit, Position In This relation, is the
position of the key in this relation.
3. Create an Output Keys Vector OKVx (contains all
keys with classification x that will appear in the
output table) for all x:
a. As having a number of bits equal to the
number of entries in Rkey,x.
b. Read all relations having an attribute
participating in the selection criteria of the
query.
c. Get all entries from those relations satisfying
the selection criteria at each level x (at level u
we have SHU-1, and APL-9; and at level c we
have CLB-2).
d. For every entry that succeeds, set its position
in OKVx to 1. The position of an entry in
OKVx can be found by matching the key of
this entry to the key in Rkey,x and getting its
position in Rkey,x.
i.OKVu = 110 (the first three keys in
Rname,u will appear in output table)
ii.OKVc = 1 (the first and only key in
Rname,u will appear in output table)
4. Create a Polyinstantiated Keys Vector, PKVx,y
that contains all polyinstantiated keys at level x by
subjects at level y, for all x,y such that x<y. For all
attributes Ai requested in the output of the query
(name, obj and des) except for the key (name) do
the following:
a. Create PKVAi,x,y = the ANDing of all
BV.RAi,x,z where x <= z < y for all z
PK obj,u,c = BV.Robj u,u AND BV.Robj,u,c
= 110 AND 001 = 000
PK obj,u,s = BV.Robj u,u AND BV.Robj,u,c
= 110 AND 001 = 000
PK obj,c,s = BV.Robj c,c AND BV.Robj,c,s
= 1 AND 1= 1
PK des,u,c = BV.Rdesu,u AND BV.Rdes,u,c
= 100 AND 011 = 000
PK des,u,s = BV.Rdesu,u AND BV.Rdes,u,c
= 100 AND 011= 000
PK des,c,s = BV.Rdes c,c = 1
b. Get PKVx.y as the ORing of all PKVAi,x.y
PKVu,c = PK obj,u,c OR PKdes,u,c = 000
PKVu,s = PK obj,u,s OR PK des,u,s = 000
PKVc,s = PK obj,c,s OR PK des,c,s = 1
A 1-bit in position n in any vector PKVx
,y
signifies that the nth entry in Rkey,x is
polyinstantiated. Therefore, entry 1 in Rname,c that
is CLB-2 is polyinstantiated.
BVA+ - A BIT VECTORS ALGORITHM FOR ACCELERATING QUERIES IN MULTILEVEL SECURE
DATABASES
497
BVA+ differs, in this step, from its predecessor.
In order to find if there are any polyinstantiated
keys, BVA creates the Polyinstantiated Key Vector
PKV, first by ORing all the Bit Vector BV.RAi’s,
then ANDing the Bit Vectors, again, with the results
of the first AND, and finally ends up by ORing all
the Polyinstantiated Key Vector PKV’s (of the
attributes) having the same classification. While the
BVA+ algorithm simply ANDs the BV.RAi’s of
each attribute and ORs the resulted PKV’s (of all the
attributes). In this way, BVA+ simplifies and
reduces the calculation, thus making it more
efficient both space and time wise.
5. Create POKVx,y (polyinstantiated output keys
vector) as the ANDing of PKVx,y and OKVx
POKVu,c = OKVu AND PKVu,c
= 110 AND 000 = 000
POKVu,s = OKVu AND PKVu,s
= 110 AND 000 = 000
POKVc,s = OKVc AND PKVc,s = 1 AND 1
=1
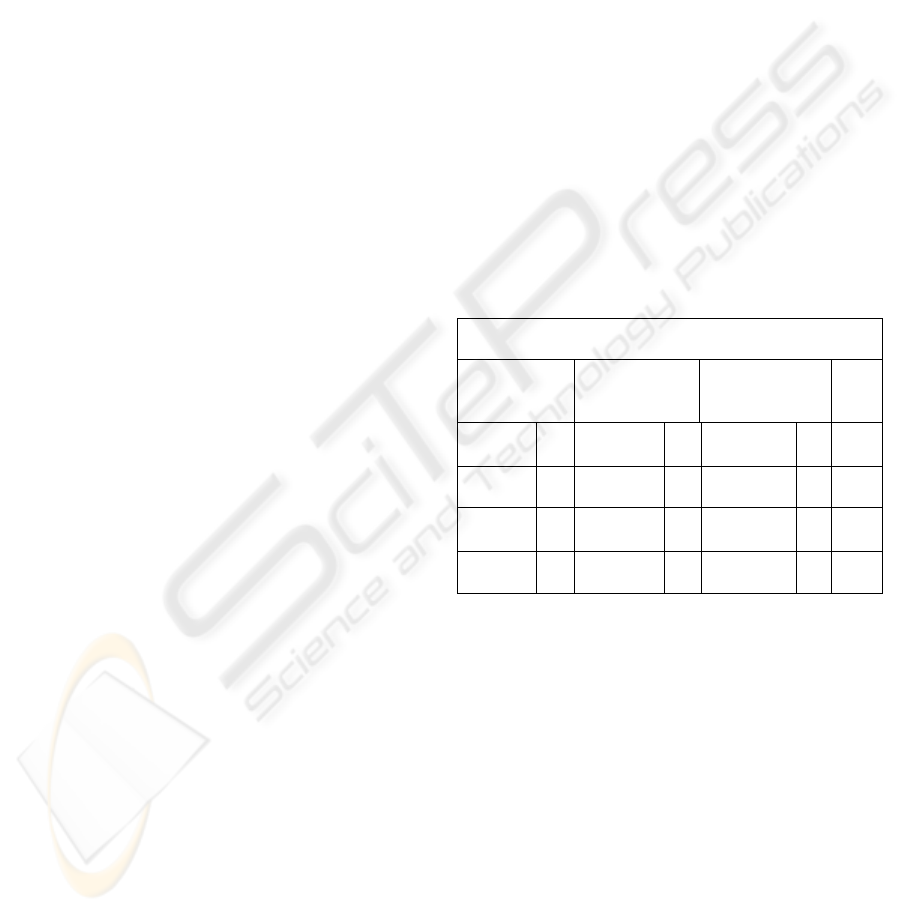
6. Create an Output table, as shown in figure 4, as
follows:
a. Having a number of columns equal to the
number of fields, Ai, requested in the output
of the query (name, obj and des) → 3
columns.
b. Scan OKVx for 1-bit entries (appears in the
output). If a 1 bit appears in position n do the
following for all Ai attributes requested in the
output:
i.If Ai is the key (i = 1) then get the nth
record from RA1,x and store it under A1
column in output table. This entry has
classification x.
ii.Else, go to the nth entry in BV.RAi,x,z
where z = x initially . If a 1 bit is found in
position n then get the pit value of the
entry in MVI.RAi,x
,z that has pib = n.
Let p = pit, get the p’th entry from
RAi,x,z and store it under Ai column in
output table. This entry has classification
z. Else (if 1 bit is not found in position n
of BV.RAi,x,z then) increment z to the
next higher level and repeats this step.
c. Scan POKVx,y for 1-bit entries (appears in
the output and polyinstantiated). If a 1 bit
appears in position n do the following for all
Ai attributes requested in the output:
i.If Ai is the key (Ai = A1) then get the nth
record from RA1,x and store it under A1
column in output table. This entry has
classification x.
ii.Else, go to the nth entry in BV.RAi,x,z
where z = y initially . If a 1 bit is found in
position n then get the pit value of the
entry in MVI.RAi,x,z that has pib = n. Let
p = pit, get the p’th entry from RAi,x,z
and store it under Ai column in output
table. This entry has classification z. Else
(if 1 bit is not found in position n of
BV.RAi,x,z
then) decrement z to the next
lower level and repeats this step. If the
BV.RAi does not exist then put a null
value under the Ai column in the output
table. This entry has classification z.
Part c, is also different from its predecessor.
Here, BVA+ requires that if the BV.RAi of any
attribute does not exist, (i.e., if it is neither 0 nor 1) a
null value under that attribute’s column is inserted.
In this way, the output given by the recovery
algorithm of BVA+ is proper and consistent with
respect to the real database. Thus, BVA+ takes care
of null values of the database, which its predecessor
– BVA – did not. The null value will have
classification z and the algorithm will be repeated
for the remaining attributes.
The output table of BVA+ algorithm, after the
above stated query, will look like:
Spaceship
Name Objective
(obj)
Destination
(des)
TC
SHU-1 U Explore U Uranus U
U
APL-9 U Mine U Neptune C
C
CLB-2 C Explore C Neptune C
C
CLB-2 C Spy S NULL S
S
5 CONCLUSION
The BVA
+
algorithm is an improvement over the
Sea View Security Model, and DVA and BVA
algorithms. Compared to the first, which was one of
the earliest and most important attempts towards
multilevel database security, the BVA
+
has the
following advantages: 1) No spurious tuples in the
output table, and 2) No time inefficiency because the
BVA
+
algorithm does not depend on the use of joins
and unions like the Sea View model to create the
output table.
When compared with the DVA algorithm, BVA+
is more space and time efficient as it eliminates the
following data structures: 1) The Domain Vector
Tables (referred to as DVTs in the DVA algorithm)
used to map keys to their positions in the primary
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
498

relations, 2) The Domain Value Indices (referred to
as DVIs in the DVA algorithm) of primary relations,
3) The Domain Vectors (referred to as DVs in the
DVA algorithm) of primary relations, 4) The
participation of primary relations in the creation of
the Polyinstantiated Domain Vectors (referred to as
PDVs in the DVA algorithm), and 5) Select Omit
Tables (referred to as SOTs in the DVA algorithm),
which are used to produce the Output table.
When compared with the BVA algorithm, BVA+
has the advantages: 1) Reduced calculations in
finding one of the temporary storage used to create
the output table, and 2) Proper output table, without
producing inconsistent data.
REFERENCES
Bell, D. and LaPadula, L., 1976. Secure computer
systems: unified exposition and Multics
interpretation. Technical Report. The Mitre
Corporation.
Haraty, R. and Rahhal, I., 2002. A bit vectors algorithm
for accelerating queries in multilevel secure
databases. Proceedings of the CSITeA 2002, Foz du
Iguazo, Brazil.
Jajodia, S. and Sandhu, R., 1991. Toward a multilevel
secure relational data model. Proceedings of the ACM
SIGMOD International Conference on Management
of Data. Denver, Colorado.
Lunt, T., Denning, D., Schell, R., Hechman, M., and
Shockley, W., 1990. The Sea View security model”.
IEEE Transactions on Software Engineering, Volume
16, Number 6.
Perrizo, W. and Panda, B., 1993. Query acceleration in
multilevel secure distributed database systems.
Proceedings of the 16
th
National Computer Security
Conference. Baltimore, Maryland.
Rahal, I. and Perrizo, W., 2003. Query acceleration in
multi-level secure database systems using the P-Tree
technology. Proceedings of The International
Conference on Computers and Their Applications
(CATA’03). Honolulu, Hawaii.
Sandhu, R., 1994. Design and implementation of
multilevel databases. Proceedings of the 6
th
RADC
Workshop on Multilevel Database Security.
Southwest Harbor, Maine.
BIOGRAPHIES
Ramzi A. Haraty is the Chairman of the Division of
Computer Science and Mathematics and an Associate
Professor of Computer Science at the Lebanese American
University in Beirut, Lebanon. He received his B.S. and
M.S. degrees in Computer Science from Minnesota State
University - Mankato, Minnesota, and his Ph.D. in
Computer Science from North Dakota State University -
Fargo, North Dakota. His research interests include
database management systems, artificial intelligence, and
multilevel secure systems engineering. He has well over
50 journal and conference paper publications. He is a
member of Association of Computing Machinery, Arab
Computer Society and International Society for Computers
and Their Applications.
Arda Zeitunlian received her B.S. degree in Computer
Science from Haigazian University in Beirut, Lebanon.
She is currently pursuing her M.S. degree in Computer
Science at the Lebanese American University. Her
research interests include database management systems
and software engineering.
BVA+ - A BIT VECTORS ALGORITHM FOR ACCELERATING QUERIES IN MULTILEVEL SECURE
DATABASES
499
