ASSESSING EFFORT PREDICTION MODELS FOR

CORRECTIVE SOFTWARE MAINTENANCE

An empirical study

Andrea De Lucia Eugenio Pompella Silvio Stefanucci

Dipartimento di Matematica e Informatica

University of Salerno

Via S. Allende, 84081 Baronissi (SA), Italy

EDS Italia Software S.p.A.

Viale Edison, Loc. Lo Uttaro

81100 Caserta, Italy

Department of Engineering

University of Sannio

Piazza Roma, 82100 Benevento, Italy

Keyw

ords: Software Engineering, Corrective Software Maintenance, Manage

ment, Cost Estimation Models

Abstract: We present an assessment of an empirical study aiming at building effort estimation models for corrective

maintenan

ce projects. We show results from the application of the prediction models to a new corrective

maintenance project within the same enterprise and the same type of software systems used in a previous

study. The data available for the new project are finer grained according to the indications devised in the

first study. This allowed to improve the confidence in our previous empirical analysis by confirming most of

the hypotheses made and to provide other useful indications to better understand the maintenance process of

the company in a quantitative way.

1 INTRODUCTION

Planning software maintenance work is a key factor

for a successful maintenance project and for better

project scheduling, monitoring, and control. To this

aim, effort estimation is a valuable asset to

maintenance managers in planning maintenance

activities and performing cost/benefits analysis. In

fact, it allows to:

• sup

port software related decision making;

• reduce project risks;

• assess the efficiency and produ

ctivity of the

maintenance process;

• manage resources and staff allocation, and so on.

Manageme

nt can use cost estimates to approve or

reject a project proposal or to ma

nage the

maintenance process more effectively. Furthermore,

accurate cost estimates would allow organizations to

make more realistic bids on external contracts.

Unfortunately, effort estimati

on is

one of the most

relevant problems of the software maintenance

process (Banker et al., 1993; Kemerer & Slaughter,

1999; Jorgensen, 1995). Predicting software

maintenance effort is complicated by the many

typical aspects of software and software systems that

affect maintenance activities. The maintenance

process can be focused on several different types of

interventions: correction, adaptation, perfection, etc.

(IEEE, 1998). Maintenance projects may range from

ordinary projects requiring simple activities of

understanding, impact analysis and modifications, to

extraordinary projects requiring complex

interventions such as encapsulation, reuse,

reengineering, migration, and retirement (De Lucia

et al., 2001). Moreover, software costs are the result

of a large number of parameters (Boehm, 1981), so

any estimation or control technique must reflect a

large number of complex and dynamic factors. The

predictor variables typically constitute a measure of

size in terms of LOC or function points (Niessink &

van Vliet, 1998) or complexity (Nesi, 1998) and a

number of productivity factors that are collected

through a questionnaire (Boehm, 1981). Quality

factors that take into account the maintainability of

the system are also considered to improve the

prediction of the maintenance costs (Granja-Alvarez

& Barranco-Garcia, 1997; Sneed, 2003).

The size of a maintenance task can also be used to

esti

te the effort required to implement the single

change (Jorgensen, 1995; Sneed, 2003). However,

while useful for larger adaptive or perfective

maintenance tasks during software evolution

(Fioravanti & Nesi, 2001), this approach is not very

attractive for managers that have to estimate the

effort required for a corrective maintenance project.

Indeed, in this case the effort of a maintenance

period greatly depends on the number of

383

De Lucia A., Pompella E. and Stefanucci S. (2004).

ASSESSING EFFORT PREDICTION MODELS FOR CORRECTIVE SOFTWARE MAINTENANCE - An empirical study.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 383-390

DOI: 10.5220/0002595603830390

 SciTePress

maintenance requests, whereas tasks of the same

type typically require a similar effort (Basili et al.,

1996; Ramil, 2000).

In a recent work (De Lucia et al., 2002), we

presented an empirical study aiming at building

corrective maintenance effort prediction models

from the experience of the Solution Center setup in

Italy (in the town of Caserta) by EDS Italia

Software, a major international software company.

This paper presents a replicated assessment of the

effort prediction models described in (De Lucia et

al., 2002). We show results from the application of

the prediction models to a new corrective

maintenance project within the same enterprise and

the same application domain as the projects used in

the previous study. The data available for the new

project were finer grained according to the

indications devised in the first study. This allowed to

improve the confidence in our previous empirical

analysis by confirming most of the hypotheses made

and to provide other useful indications to better

understand the maintenance process of the company

in a quantitative way.

The paper is organized as follows. Sections 2 and 3

report the experimental setting and the results of the

previous experimental study, respectively. Section 4

describes the new project, while Sections 5-7 present

and discuss the results achieved through the analysis

of the finer grained data available for the new

maintenance project. Concluding remarks are

outlined in Section 8.

2 EXPERIMENTAL SETTING

Most of the business of the subject company

concerns maintaining third party legacy systems.

The subject company realizes outsourcing of system

conduction and maintenance, including help desk

services, for several large companies. Very often the

customers ask for a very high service agreement

level and this requires an accurate choice and

allocation of very skilled maintainers, with adequate

knowledge of the application domain and

programming language of the maintenance project.

This implies a careful definition of the maintenance

process with well-defined activities, roles, and

responsibilities to avoid inefficiencies (Aversano et

al., 2002). The phases of the life-cycle of the

ordinary maintenance process are shown in Table 1.

They closely follow the IEEE Standard for Software

Maintenance (IEEE, 1998).

The data set available for our study is composed of a

number of corrective software maintenance projects

conducted on software systems of different

customers. The subject systems are mainly business

applications in banking, insurance, and public

administration. These projects allow for general

conclusions that can be applied to other corrective

maintenance projects in the business application

domains of the subject company.

Table 1: Phases of the corrective maintenance process

Phase Short description

Define

Requirements identification and definition

Analyze

Requirements analysis

Design

Design of software modules and test cases

Produce

Implementation of software modules and

execution of test cases

Implement

Delivery and introduction of the new modules in

the software system

The main advantage of the data set is that it does not

contain missing values. This is due to the careful

manner in which the data was collected. In fact, the

subject company is at CMM level 3 and is currently

planning the assessment to achieve CMM level 4. At

the CMM level 3, metrics are collected, analyzed,

and used to control the process and to make

corrections to the predicted costs and schedule, as

necessary. Therefore, metric collection was crucial

and supported by automatic tools, such as workflow

management systems which are of aid to process

automation and improvement (Aversano et al.,

2002). Technical metrics, such as software

complexity metrics, were not available. In fact, for

each new maintenance project, the subject company

preliminarily collects a number of different technical

metrics on a meaningful subset (about 20%) of the

application portfolio to be maintained. The goal is to

make an assessment of the software systems to make

decisions about negotiations of the customer service

levels, and to select the skills required by the

maintenance team (De Lucia et al., 2001).

3 PREVIOUS EMPIRICAL STUDY

In a previous work (De Lucia et al., 2002), the data

of five corrective maintenance projects was used in

an empirical study aiming at constructing effort

prediction models. We used multiple linear

regression analysis to build prediction models and

validated them on the project data using cross-

validation techniques (Bradley & Gong, 1983).

The data set was composed of 144 monthly

observations, collected from all the projects. For

each observation, corresponding to monthly

maintenance periods for each project, the following

data was available and considered in our analysis

(see Table 2):

• size of the system to be maintained;

• effort spent in the maintenance period;

ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

384

• number of maintenance tasks, split in three

categories:

type A: the maintenance task requires software

source code modification;

type B: the maintenance task requires fixing of

data misalignments through database queries;

type C: the maintenance task requires

interventions not included in the previous

categories, such user disoperation, problems

out of contract, and so on.

The cost estimation model previously used within

the organization was based on the size of the system

to be maintained and the total number of

maintenance tasks. For this reason we decided to

build a linear model taking into account these two

variables (model A in Table 3). However, we

observed that the effort required to perform a

maintenance task of type A might be sensibly

different than the effort required to perform a task of

type B or C. Also the number of maintenance tasks

of type A is sensibly lower than the number of

maintenance tasks of the other two types. For this

reason, we expected to achieve a sensible

improvement by splitting the variable N into the two

variables NA and NBC (see Table 2). The result of

our regression analysis was model B in Table 3.

Finally, we also built a model considering the effect

of each different type of maintenance tasks (model C

in Table 3), although this model is generally more

difficult and risky to be used, because it requires

more precise estimates of the number of tasks of

type B and C. Indeed, the coefficients of this model

seem to suggest that the effort required for these two

types of maintenance tasks is different: in particular,

tasks of type C seem to be more expensive than

tasks of type B.

To evaluate the prediction performance, we

performed cross-validation and computed MRE

(Magnitude Relative Error) for each observation,

MMRE (Mean Magnitude Relative Error) and

MdMRE (Median Magnitude Relative Error).

The MRE

on an observation i is defined as:

MRE

−

where y

is the value of the i-th value of the

dependent variable as observed in the data set and ŷ

is the corresponding value predicted by the model.

MMRE is the average of the MRE

, while MdMRE

is the median of the MRE

Moreover, the following variants of the measure

PRED (Conte et al., 1986; Jorgensen, 1995) were

computed:

• PRED

= % of cases with MRE <= 0.25.

• PRED

= % of cases with MRE <= 0.50.

The MMRE, MdMRE, and PRED measures

resulting from the leave-one-out cross-validation are

shown in Table 4.

The prediction performances of our models are

nevertheless very interesting according to the

findings of Vicinanza et al. (1991), in particular

considering that what is really wanted by software

management is not to predict accurately, but to

control over the final results.

Table 2: Collected metrics

Metric Description

NA # of tasks requiring software modification

NB # of tasks requiring fixing of data misalignment

NC # of other tasks

NBC NBC=NB+NC

N N=NA+NB+NC

SIZE Size of the system to be maintained [kLOC]

EFFORT Actual Effort [man-hours]

Table 3: Effort prediction model parameters

Model Var. b

(Coeff.) p-value R

Adj R

SIZE

1.342904

0.169086

<10E-07 0.8257 0.8245

NBC

SIZE

9.053286

0.138275

1.164826

<10E-07

0.8891 0.8876

SIZE

7.86988

0.514121

2.81486

0.130507

<10E-07

0.000001

<10E-07

0.8963 0.8941

Table 4: Model predictive performances

Model A Model B Model C

MMRE 42.53% 36.40% 32.25%

MdMRE 37.57% 29.16% 25.35%

PRED

31.25% 40.36% 49.31%

PRED

66.75% 74.56% 82.64%

4 NEW EMPIRICAL STUDY

The main limitation of the data set was the fact that

only the total effort of each maintenance period was

maintained, while data for the single maintenance

tasks was not available.

Indeed, it would have been interesting to increase

the granularity of the collected data, also considering

the effort of all the tasks of the same type or, even

better, the effort of the single maintenance task. The

availability of this data would allow to:

• validate our hypothesis of considering different

maintenance task types in the cost estimation

models;

ASSESSING EFFORT PREDICTION MODELS FOR CORRECTIVE SOFTWARE MAINTENANCE - AN EMPIRICAL

STUDY

385

• assess the different task types in a quantitative

way;

• discover outliers at different granularity levels,

both for monthly observations, and for single

maintenance requests;

• understand the process in a quantitative way.

To overcome the limitations of the first study

concerning the granularity of the data, the subject

company implemented a specific process

management tool (PMT) and used it in a new

maintenance project. The PMT is web-based and is

used at three different geographical sites,

corresponding to the different Solution Centers

involved in this new project. Its main capabilities are

recording time and effort needed to carry out each

phase of the maintenance process, notifying events

to the maintenance team members responsible to

perform a task when this has to be started,

interfacing existing tools for configuration

management, tracking maintenance requests.

Each maintenance request coming from the

customer is recorded by a fist level Help Desk using

a tracking tool that is on-line consulted only on one

site by the software analysts responsible for this

maintenance project. The analysts have two options:

accepting the request and routing it to other sites or

discarding the request and providing the motivations

directly to the Help Desk tracking tool. Each

accepted request is assigned a typology, that can be

Change (small evolution), Defect (trouble ticket), or

Other. Moreover, if the request is classified as

Defect, there are other attributes specifying the

severity and the associated priority (High, Medium,

Low). The maintenance process is composed of a set

of phases (shown in Table 1), again decomposable in

a set of elementary activities based on the typology

of the maintenance request. Each phase can be

assigned to different human resources allocated on

the project.

The new project was still on when we started the

empirical study, so the data concerning the first 6

months of the project were available. The PMT

allowed to collect about 30,000 observations,

concerning 7,310 maintenance requests received in

these 6 months. In this case, each observation

corresponds to one phase of the maintenance process

applied to a maintenance request, while in the

previous empirical study it corresponded to the

aggregation of all the maintenance requests received

in one month. For each maintenance request the

following data was available:

• Effort spent on each phase of the maintenance

process (measured in man-hours);

• Priority, split in three categories:

High: anomalies that entail the total

unavailability of the system;

Medium: anomalies that entail the partial

unavailability (one or more functions) of the

system;

Low: anomalies that do not entail blocks of the

system’s functions, but degrade the

performances of the system or cause incorrect

operations or are limited to the user interface.

Table 5 shows the descriptive statistics for the

monthly metrics of this maintenance project.

Table 5: Descriptive statistics of the new project

Metric Min Max Mean Median Std.Dev.

NA 66 96 83.33 83.5 10.23

NB 276 472 353.83 348 69.39

NC 625 927 780.5 782 104.23

N 967 1423 1217.67 1223 164.51

EFFORT 3225 4857 3812.5 3768 539.58

5 ASSESSING PREDICTIVE

PERFORMANCES ON THE NEW

PROJECT

Our first analysis was evaluating the predictive

performances of the models built in De Lucia et al.

(2002) on the new maintenance project. We applied

the models to the new data simulating their behavior

as it was really applied for prediction purposes. In

fact, for the first monthly observation we used

directly the models and coefficients of Table 3; for

the next observation, we added previous

observations to the data learning set of the model

and recalibrated the models calculating the

coefficients again. Results are shown in Table 6.

Table 6: Assessed model predictive performances

Model A Model B Model C

MMRE 36.91% 31.40% 16.60%

MdMRE 32.31% 27.29% 14.31%

PRED

0.00% 33.33% 83.33%

PRED

66.66% 66.66% 100.00%

For the best model (model C) only one prediction

falls outside the 25% wall, producing a PRED

value of 83.33%. The MRE of each observation is

reasonably low for all the predictions: if we discard

the worst prediction (MRE = 35.56%), the MRE has

a maximum value of 21.00%, that is surely an

acceptable error value for the software maintenance

effort prediction. The mean MRE is 16.60%, again

an excellent value. It is worth noting that although

the number of monthly periods is small, the

ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

386

performance parameters in Table 6 exhibit the same

positive trends as in the previous study (see Table

4), in particular concerning MMRE e MdMRE.

However, the small number of monthly periods

seems to be the main reason for the greater

variations of the PRED measures.

Our previous work was centered on the model

construction and assessment of the prediction

performance through cross-validation (Bradley &

Gong, 1983). In this paper the granularity of the data

collected for the last software project allows us to

make further analyses: we have useful data to

confirm (or to reject) the basic hypothesis of the

effort prediction model, namely the assumption that

the tasks of different type require different effort to

be made and, in particular, tasks of type A generally

require greater effort than the other two types. The

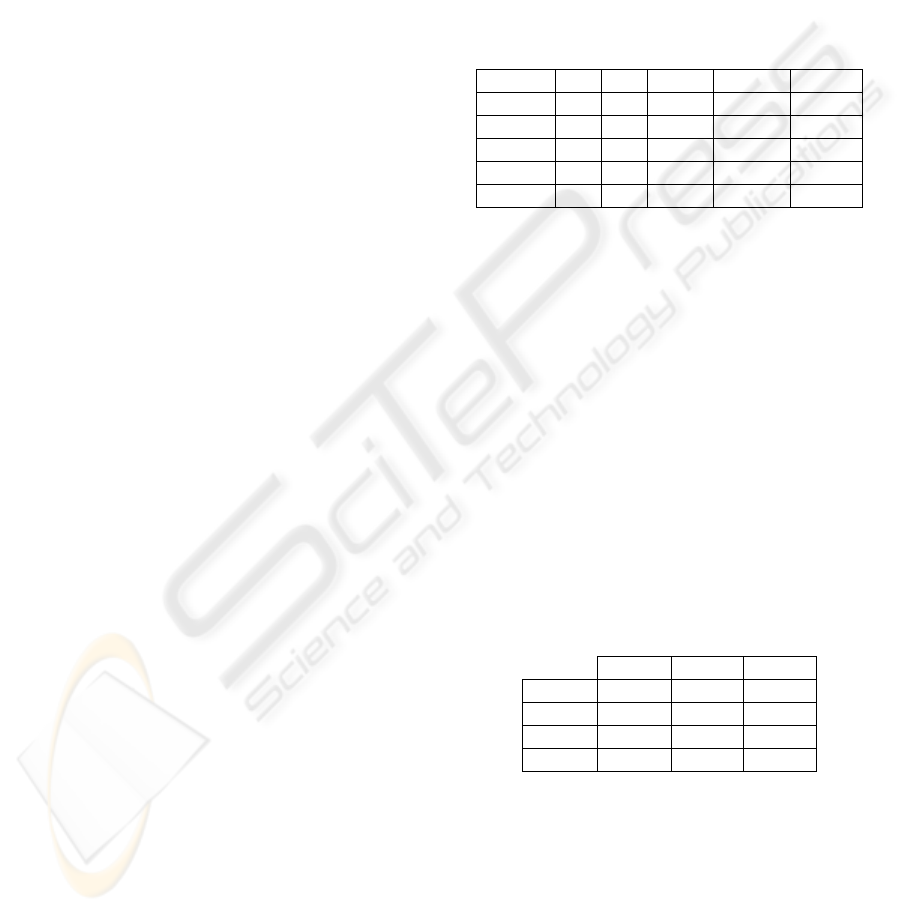
box plot of Figure 1 and the data in Table 8 clearly

confirm this hypothesis and provide us with a lot of

other information about the maintenance process.

Each type of task has mean and median values

sensibly different and presents a higher value for the

coefficient of variation (it is the ratio of standard

deviation by mean), thus indicating the presence of

statistical outliers. However, rather than discarding

all statistical outliers, we decided to analyze the data

in a flexible way: we only discarded the

maintenance requests with an effort that was clearly

abnormal compared with all the other observations.

These outliers represent isolated points with very

high effort values almost of one magnitude order

greater than the other observations (including other

statistical outliers). On the other hand, besides

abnormal outliers, it is common to have a relatively

small number of maintenance requests requiring a

great effort (compared to mean value); therefore, if

we had discarded from our analysis also these

observations that can be considered as outliers by a

pure statistical point of view, we would have surely

lost useful information about the software

maintenance process.

It is worth noting that the effort required to

accomplish the maintenance tasks corresponding to

abnormal outliers is very large (almost two

magnitude order greater than the mean). These

maintenance requests can be easily identified as

soon as they begin to be worked, as their resolution

is usually non standard and requires more complex

analysis and design. Sometimes, they are

programmed maintenance requests, such as database

restructuring operations. These can be viewed as the

perfective interventions auspicated by Lehman’s

laws of software evolution to deal with the

increasing complexity and declining quality of the

software systems (Lehman & Belady, 1985). For this

reason, the effort of these maintenance tasks should

not be considered in the prediction model; rather, a

project manager should account for a small number

of such tasks when estimating the effort of the

maintenance project.

According to this heuristic we identified five

outliers, corresponding to five maintenance requests,

one of type A, three of type C and one of type B.

After this elimination we recalibrated the effort

prediction models and obtained the new relative

errors shown in Table 7: the performance values are

improved in all the parameters, although slightly.

Moreover, if we consider the model C, MRE

sensibly decreases for all the months which have an

outlier discarded; in particular, the maximum value

of the monthly MRE shrinks from 35.56% to

26.48%.

Table 7: Assessed model predictive performances

(without outliers)

Model A Model B Model C

MMRE 37.72% 28.06% 15.69%

MdMRE 38.68% 30.40% 13.56%

PRED

16.66% 33.33% 83.33%

PRED

66.66% 83.33% 100.00%

6 ANALYSIS OF TASKS OF

DIFFERENT TYPES AND

PRIORITY

In this section we analyze the distribution of the

effort among tasks of different type and priority. As

shown in Figure 1, the height of the NA box

indicates that tasks of type A have higher variability

than the tasks of other types. Generally, this type of

tasks:

• requires an effort great almost five or six times

the effort required by the other two types, as it

can be noted by comparing the values of the

quartiles, of the medians, and of the box fences

(adjacent values);

• has effort value ranges clearly higher than the

other two types;

• has the main influence on the effort.

This confirms our hypothesis about the different

influence on the effort determined by the type of

tasks.

The other two types of tasks have similar boxes,

indicating that the tasks of type B and C:

• generally require similar effort to be made, with

a slight adjunctive effort for type B;

• have a small variability range, as the efforts of

the maintenance tasks comprised between the

10th and 90th percentiles range between 0.4 and

ASSESSING EFFORT PREDICTION MODELS FOR CORRECTIVE SOFTWARE MAINTENANCE - AN EMPIRICAL

STUDY

387

4 hours for maintenance tasks of type B and

between 0.4 and 3 hours for maintenance tasks of

type C (see Table 8).

Figure 1: Effort distribution box plot with respect to

maintenance request types

Table 8: Effort distribution among task types

NA NB NC

Mean 12.78 2.43 1.94

StDev 20.30 6.86 7.25

Percentile 1.75 0.40 0.40

Median 6.75 1.20 1.00

Percentile 30.00 4.00 3.00

A consideration to make is the fact that while the

coefficients of model C in Table 3 seems to suggest

that in the previous projects the effort required for

tasks of type C is greater than the effort required for

tasks of type B, the detailed data of the new project

seems to confute this hypothesis, as maintenance

tasks of type B and C require a similar effort

(slightly higher for tasks of type B). Therefore, the

major improvement of model C with respect to

model B (compare Tables 4 and Table 6) was

unexpected, as the data of the new project seems to

justify the aggregation of the tasks of type B and C

and its use as a single variable in the prediction

model B. The reason of the major improvement of

the performances of model C can be justified by a

compensation effect of the coefficients of the model.

It is worth noting that due to the similarity of the

efforts of maintenance tasks of type B and C and due

to the fact that the number of maintenance tasks of

type C is about twice the number of maintenance

tasks of type B, applying model C is equivalent to

apply model B with a lower coefficient for NA and a

higher coefficient for NBC (see Table 3). Therefore,

giving a greater weight to tasks of types B and C

with respect to tasks of type A would result in better

performances of model B in the new project.

The classification of each request by priority allows

to make further considerations about the

maintenance process execution. Almost all the

outliers do not have high priority. From Table 9 and

Table 10 there is a low percentage of high priority

tasks. The larger part of the effort is spent on the low

priority tasks, which are resolved after an accurate

scheduling of the activities. It is worth noting that,

among the low priority tasks, the tasks of type A

account only for 4.64% of the total number of

maintenance requests, but consume 22.93% of the

total effort. This suggests that a big part of

maintenance requests that impacts on software code

has low priority and a complexity level not trivial, as

they need more effort to be made.

Table 9: Task type and priority distribution (%)

Type A Type B Type C

High priority 0.60 2.18 2.08

Medium priority 1.59 3.97 15.35

Low priority 4.64 22.91 46.66

Table 10: Effort distrib. (%) among task type and priority

Type A Type B Type C

High priority 2.23 4.12 1.96

Medium priority 5.80 4.03 12.40

Low priority 22.93 16.90 29.62

7 EFFORT DISTRIBUTION

ANALYSIS

In this section we analyze the data about the

distribution of the effort to the phases of the

maintenance process. Figures 2 and 3 show the

phase distribution distinguishing the tasks of type A

from the tasks of type B and C. This distinction is

needed because the maintenance process for a task

of type A requires software code modifications: this

operation and all the strictly correlated activities

(such as document check-in/check-out, testing

execution, etc.) are included in the phase called

Produce, that is not present in the other task types.

There are not unexpected results: for type A the

Produce phase is the most expensive, as it can be

seen from the height of the box and of the upper

fence. This is reasonable, as the effort needed for

testing (that generally is an expensive operation), is

accounted in this phase.

For type B and C the phase distribution is almost

regular: all the boxes have similar height and have

median value at 25%; there are no high values for

the fences, and the phases require analogous time to

be executed, with Analyze and Design generally

more expensive than Define and Implement.

It is worth noting that the phases of the maintenance

process for the tasks of type B and C have a very

short time. In most cases, they are performed in less

than one hour. In this case, the phase distribution

ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

388

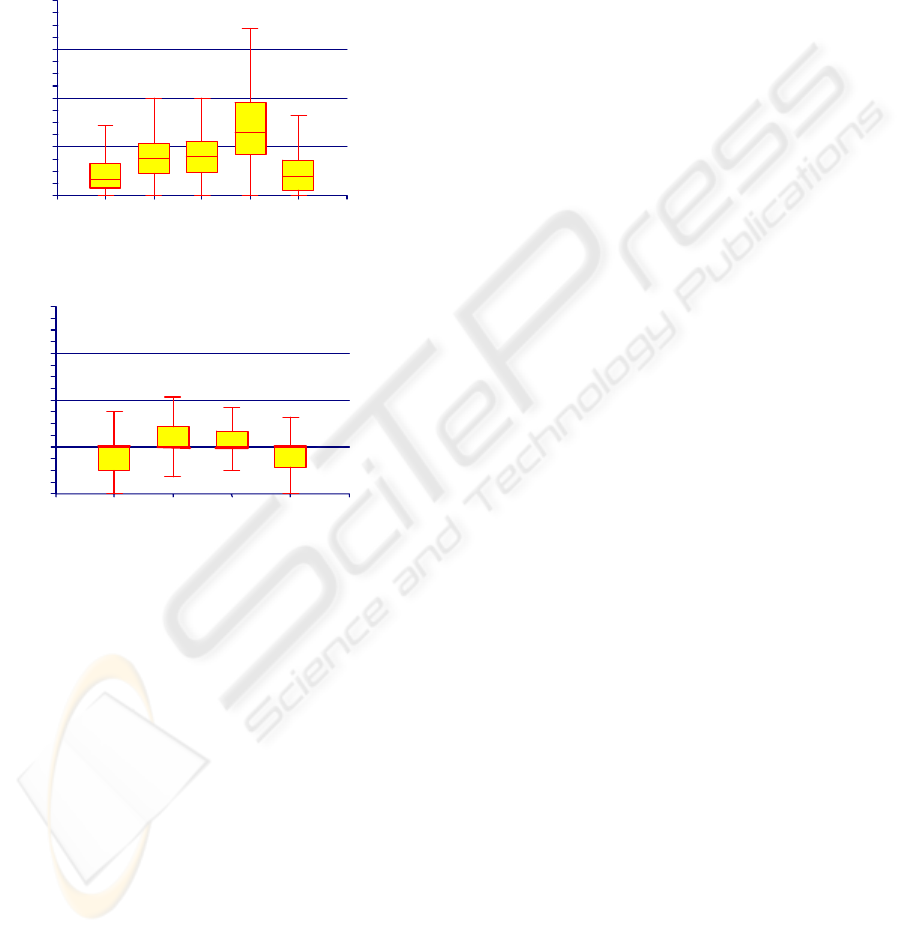
analysis clearly shows that there is no real utility to

perform analyses aiming at reducing the time needed

for the completion of a single phase. On the other

hand, it is useful to analyze them to discover

particular trends or phase distribution correlated to

specific process characteristics. In our case, we have

not discovered any of these properties, so we have

limited our discussion to the simple description of

the time distribution among the different phases.

Figure 2: Effort distribution box plot with respect to

phases (maintenance requests of type A)

Figure 3: Effort distribution box plot with respect to

phases (maintenance requests of type B and C)

8 CONCLUSION

In this paper we have presented an assessment of an

empirical study aiming at building corrective

maintenance effort estimation models. In a previous

work (De Lucia et al., 2002) we used as a case study

a data set obtained from five different corrective

maintenance projects to experimentally construct,

validate, and compare model performances through

multivariate linear regression models. The main

observation was to take into account the differences

in the effort required to accomplish tasks of different

types. Therefore, we built effort prediction models

based on the distinction of the task types. The

prediction performance of our models was very

interesting according to the findings of Vicinanza et

al. (1991).

A critique to the applicability of the cost estimation

models might be the fact that they consider as

independent variables the number of maintenance

tasks that are not known at the beginning of a project

and that should be in turn estimated. However, as far

as our experience with these type of systems has

demonstrated, the overall trend of the maintenance

tasks of each type appears to follow the Lehman’s

laws of software evolution (Lehman & Belady,

1985), in particular the self regulation and the

conservation of organizational stability laws: in

general the number of maintenance tasks of each

type oscillates around an average value across the

maintenance periods. These average values can be

calculated with a good approximation after a few

maintenance periods and used to estimate the

maintenance effort. Both the average values and the

effort estimates can be improved as soon as new

observations are available. A deeper discussion of

this issue is out of the scope of this paper. More

details and empirical data are available from the

authors.

0,0

25,0

50,0

75,0

100,0

Define Anal yze Design Produce Impl ement

Phases

Although the results of the previous study were

good, we identified some limitations concerning the

granularity of the metrics used in the previous

empirical study and auspicated the collection of

further information useful to overcome them. The

subject company is currently planning the

assessment to move from CMM level 3 to CMM

level 4. It is a requisite of the CMM level 3 that

metrics are to be collected, analyzed, and used to

control the process and to make corrections on the

predicted costs and schedule, if necessary.

Therefore, metric collection was crucial. The study

presented in (De Lucia et al., 2002) suggested to

record process metrics at a finer granularity level

than a monthly maintenance period. The subject

company applied these considerations in the

definition of the metric plan of a new maintenance

project, analyzed in this paper: productivity metrics

have been collected and recorded for each

maintenance request, allowing to obtain more

accurate productivity data. Therefore, we performed

a replicated assessment of the effort prediction

models on a new corrective maintenance project.

Thanks to the finer data, we have been able to:

0,0

25,0

50,0

75,0

100,0

Define Analize Design Impl em ent

Phases

• verify the prediction performances of the models

on a new maintenance project, applying the

effort prediction model to the new project data;

• verify the hypothesis of the different effort

needed by the tasks of different types in a

quantitative way, measuring the effort required

by the different task types;

• identify outliers in the data at a finer granularity

level, analyzing the single maintenance request

instead of their aggregation;

ASSESSING EFFORT PREDICTION MODELS FOR CORRECTIVE SOFTWARE MAINTENANCE - AN EMPIRICAL

STUDY

389

• improve the understanding of the corrective

maintenance process and its trends, by analyzing

the distribution of the effort among the different

process phases and different types and priorities

of the maintenance tasks.

At the end of the assessment on the new project we

had confirmation both of goodness of the prediction

performances of the estimation models and of the

validity of our hypotheses (different task types

require different effort). From the distribution of the

effort among the phases of the process, we also had

evidence that the corrective maintenance process

under study was quite stable. This is due to the long

dated experience of the subject company and its

maintenance teams in conducting corrective

maintenance projects. Perhaps, this is one of the

reasons why the company does not collect data for

this type of projects concerning other factors, such

as personnel skills that also generally influence

maintenance projects (Jorgensen, 1995). This lack of

available metric data is a limitation that should be

considered before using the estimation models

derived from our study outside the subject company

and the analyzed domain and technological

environment.

Future work will be devoted to introduce further

metric plans in the maintenance projects of the

subject organization. Besides statistical regression

methods, we aim at investigating other techniques.

For example, dynamic system theory can be used to

model the relationship between maintenance effort

and code defects (Calzolari et al., 2001).

REFERENCES

Aversano, L., Canfora, G., De Lucia, A., & Stefanucci, S.

(2002). Automating the Management of Software

Maintenance Workflows in a Large Software

Enterprise: a Case Study. Journal of Software

Maintenance and Evolution: Research and Practice,

14(4), 229-255.

Basili, V., Briand, L., Condon, S., Kim, Y.M., Melo,

W.L., & Valett, J.D. (1996). Understanding and

Predicting the Process of Software Maintenance

Releases. Proc. of Int. Conf. on Software Engineering,

Berlin, Germany, pp. 464-474.

Banker, R.D., Datar, S.M., Kemerer, C.F., & Zweig, D.

(1993). Software Complexity and Maintenance Costs.

Communications of ACM, 36(11), 81-94.

Boehm, B.W. (1981). Software Engineering Economics.

Prentice-Hall Inc., Englewood Cliffs, N.J., 1981.

Bradley E., & Gong, G. (1983). A Leisurely Look at the

Bootstrap, the Jack-Knife and Cross-Validation. Amer.

Statistician, 37(1), 836-848.

Calzolari, F., Tonella, P., & Antoniol, G. (2001).

Maintenance and Testing Effort Modelled by Linear

and Non Linear Dynamic Systems. Information and

Software Technology, 43(8), 477-486

Conte, S., Dunsmore, H., & Shen, V. (1986). Software

Engineering Metrics and Models. Benjamin-

Cummings Publishing Company, 1986.

De Lucia, A., Fasolino, A., & Pompella, E. (2001). A

Decisional Framework for Legacy System

management. Proceedings of IEEE Int. Conf. on

Software Maintenance, Florence, Italy, pp. 642-651.

De Lucia, A., Pompella, E., & Stefanucci, S. (2002).

Effort Estimation for Corrective Software

Maintenance. Proc. of Int. Conf. on Software

Engineering and Knowledge Engineering, Ischia,

Italy, pp. 409-416.

Fioravanti, F. & Nesi, P. (2001). Estimation and

Prediction Metrics for Adaptative Maintenance Effort

of Object-oriented Systems. IEEE Trans. on Software

Engineering, 27(12), 1062-1084.

Granja-Alvarez, J.C. & Barranco-Garcia, M.J. (1997). A

method for estimating maintenance cost in a software

project: a case study. Journal of Software

Maintenance: Research and Practice, 9(3), 161-175.

IEEE Std. 1219-1998 (1998). Standard for Software

Maintenance, IEEE CS Press, Los Alamitos, CA.

Jorgensen, M. (1995). Experience With the Accuracy of

Software Maintenance Task Effort Prediction Models.

IEEE Trans. on Software Engineering, 21(8), 674-681.

Kemerer, C.F. & Slaughter, S. (1999). An Empirical

Approach to Studying Software Evolution. IEEE

Trans. on Software Engineering, 25(4), 493-509.

Lehman, M. & Belady, L. (1985). Program Evolution:

Processes of Software Change. Academic Press,

Austin, 1985.

Niessink, F. & van Vliet, H. (1998). Two Case Studies in

Measuring Maintenance Effort. Proc. of IEEE Int.

Conf. on Software Maintenance, Bethesda, Maryland,

USA, pp. 76-85.

Nesi, P. (1998). Managing Object Oriented Projects

Better,

IEEE Software, 15(4), 50-60.

Ramil, J.F. (2000). Algorithmic Cost Estimation Software

Evolution. Proc. of Int. Conf. on Software

Engineering, Limerick, Ireland, pp. 701-703.

Sneed, H.M. (2003). Software Maintenance Cost

Estimation. Advances in Software Maintenance

Management: Technologies and Solutions. M. Polo

editor, Idea Group Publishing, USA, pp. 201-227.

Vicinanza, S., Mukhopadhyay, T., & Prietula, M. (1991).

Software Effort Estimation: an Exploration Study of

Export Performance. Information System Research,

2(4), 243-262.

ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

390