
A COMPARISON BETWEEN THE PROPORTIONAL KEEN
APPROXIMATOR AND THE NEURAL NETWORKS LEA
RNING
METHODS
Peyman Kabiri
College of Computer Engineering, Iran’s University of Science and Technology, Narmak, Tehran, Iran
K
eywords: Machine Learning, Data Visualisation and Approximation.
Abstract: The Proportional Keen Approximation method is a young learning method using the linear approximation to
learn hypothesis. In the paper this methodology will be compared with another well-established learning
method i.e. the Artificial Neural Networks. The aim of this comparison is to learn about the strengths and
the weaknesses of these learning methods regarding different properties of their learning process. The
comparison is made using two different comparison methods. In the first method the algorithm and the
known behavioural model of these methods are analysed. Later, using this analysis, these methods are
compared. In the second approach, a reference dataset that contains some of the most problematic features
in the learning process is selected. Using the selected dataset the differences between two learning methods
are numerically analysed and a comparison is made.
1 INTRODUCTION
In a research aimed to compensate for the errors due
to the flexibility and the backlash in mechanical
systems (Kabiri, 2002), and after unsuccessful
implementation of the Artificial Neural Networks
(ANN), attention was focused on finding a more
suitable method. By the ANN, the author means the
Back Propagation (BP) model of the ANN. The aim
for that research was to compensate for the
positioning errors of a robotic arm by considering it
as a Black Box (Mingzhong, 1997). After much
research using linear approximation methodology a
novel machine learning method was developed and
implemented (Kabiri, 1998 & 1999). This approach
provides the adaptability feature for the controller
but requires a large population of samples. The need
for simplicity in the data set might be the reason
why previously the researchers were only using this
approach for the joints of the manipulator (Chen,
1986). Main problems with the ANN were its slow
training and difficulty in training it with complicated
patterns in the dataset (Kabiri, 1998)(Sima, 1996).
Once the population of the dataset increases, these
problems will get worse. The Proportional Keen
Approximator (PKA) has no training stage as in the
ANN and at the most problematic areas for the ANN
it can work without any problems. On the other hand
this method has some limitations of its own, some of
which might be handled in future e.g. requires more
memory than the ANN and needs tabulated sampled
dataset. As it will be described in the following
section the early version of the PKA was introduced
in the Cartesian co-ordinate system (Kabiri, 1998).
The basic cell had two inputs and one output. Later a
new version with three inputs and one output was
introduced. Currently the work is being continued to
extend the PKA into the Spherical and Cylindrical
co-ordinate systems that will broaden its scope of
application. The PKA in the Cartesian co-ordinate
system is implementing the linear approximation to
interpolate between the sample points. The PKA is a
Memory-Based Learning (MBL) system and
requires large memory capacity (Schaal, 1994).
At the following sections the reader will first
learn about the PKA methodology. The properties of
these methods are compared both in numerical and
descriptive ways. Using a sampled dataset derived
from an equation, the ANN and the PKA
methodologies are compared numerically against
each other and results are presented.
159
Kabiri P. (2004).
A COMPARISON BETWEEN THE PROPORTIONAL KEEN APPROXIMATOR AND THE NEURAL NETWORKS LEARNING METHODS.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 159-164
DOI: 10.5220/0002599401590164
Copyright
c
SciTePress
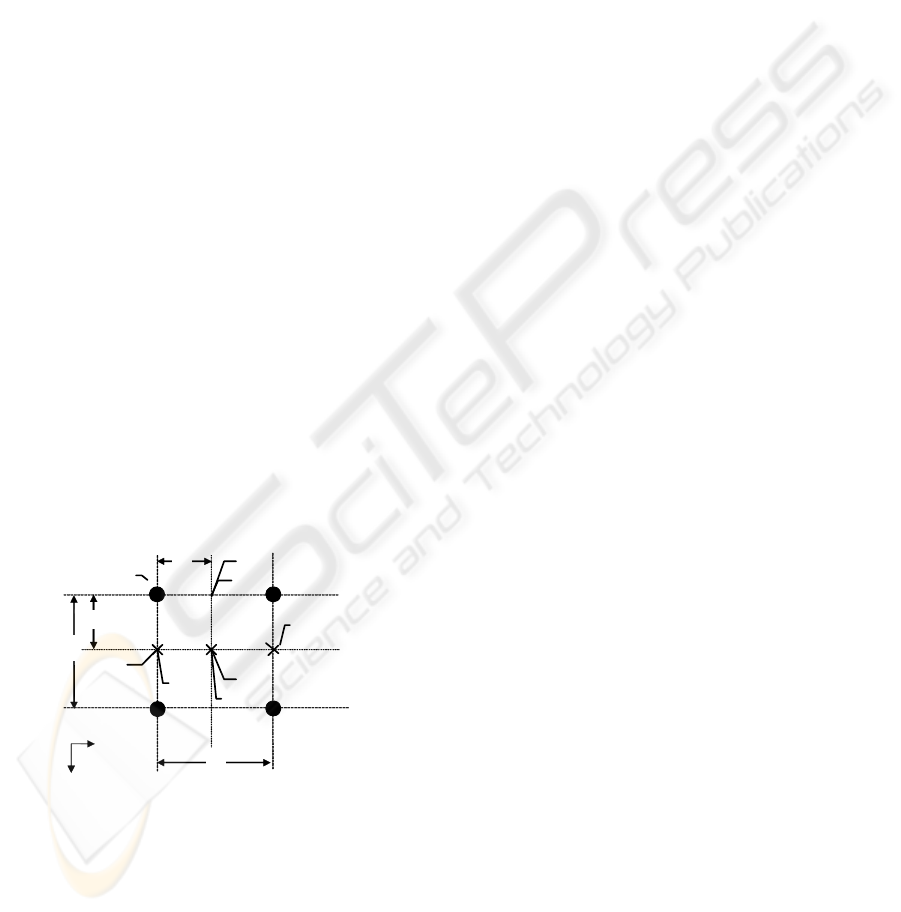
2 2D-PKA IN CARTESIAN CO-
ORDINATES SYSTEM
This Approximator is designed for 2 input and 1
output configuration (2D). Later it was expanded to
3 input and one output configuration (3D). In the 2D
configuration as it is illustrated in Figure 1, for every
ordered pair of (x, y) in the function domain, output
of the system can be calculated considering three
conditions:
Condition 1. Both of the x and y are available in
the sampled data set area. In this condition, the
output will be the actual given data sample.
Therefore, the accuracy is matched by default 100%
e.g. A (x
1
, y
1
, z
1
) in Figure 1.
Condition 2. One of the input components (x or y)
overlays one of the Rows or Columns in the given
data sample. If the given point has either of the x or
y components equal to one of the components of the
sampled data, this condition will be triggered. For
example, if the ordered pair of (x, y) is considered as
input and z considered as the data component that
determines the amount of error in that location. The
output is calculated with respect to two adjacent
neighbours of the given point. Only values of the
two unequal components (in the sample and the
given data pairs) are used for the calculations. For
example, let
21
xx = for the pairs (x
1
, y
1
) and (x
2
,
y
2
). Then for calculating the output only the y
components are used. e.g.
B (x
1
+∆x, y
1
, z
B
) when
21
xx = and
C (x
1
, y
1
+∆y, z
C
) when
21
yy = .
Condition 3. None of the input co-ordinates are
equal to any of the Rows or Columns in the
Approximator. In this condition the method will be
applied to one of the components (x or y) first. Then
the result of the calculation is used for the
proportional approximation on the other pair of
components (same as condition 2). In this condition
the output value is calculated by D (x
1
+∆x, y
1
+∆y,
z
C
) i.e. output = z
C
in Figure 1.
3 METHODOLOGY OF 3D-PKA
The main difficulty for understanding the 3D-PKA
is the visualisation of the method that is going to be
explained at the following. The key point to
understand the idea of expanding the PKA into the
3
rd
dimension is to consider each 2D-PKA as a plane
surface. Here instead of points, flat surfaces are
considered and the rest is similar to the 2D-PKA
(Kabiri, 1999). Figure 2 illustrates the concept. A
point can either be on the top or the bottom layer, or
it can be between the two layers. In the first two
cases the estimated value is the returned value from
the 2D-PKA cell (either the top or the bottom layer
that holds the point) i.e. Condition 1. However for
the third case the estimated value is the result of a
linear approximation between the results out of both
top and bottom 2D-PKA layers i.e. Condition 2. It
should be noted that as the number of dimensions
increases, the required computation power for the
method increases as well. The same is with the
memory requirements for the 3D-PKA.
4 PROPERTIES OF THE PKA
In the ANN the number of links and nodes in the In
the ANN the number of links and nodes in the
network depends on the complexity of the training
data set. Therefore the execution speed for the ANN
is directly related to the complexity of the training
data set. However, only one PKA cell is required to
learn the pattern regardless of the complexity of the
sampled data set. This means that in the PKA
method, speed is independent from the complexity
of the sampled data set. Since the number of
operations in this method is smaller and due to the
simplicity of these operations
1
, the PKA in the
forward execution needs less calculation power than
the other alternative methods such as the ANN
(particularly in 3D). In the worst case scenario
A
C
B
D
y
1
y
2
x
1
x
2
z
1
z
2
1
z
3
z
4
∆
y
∆
x
z
C2
z
C
z
B
z
D
L
y
L
x
Y
X
r and c are Row and Column
z
1
, z
2
, z
3
, and z
4
are values of the sampled points where
()()
xB
Lxzzzz /*
121
∆−+= ,
()()
yC
Lyzzzz /*
131
∆−+= ,
()()
yC
Lyzzzz /*
2422
∆−+= , and
()()
xCCCD
Lxzzzz /*
2
∆−+= ; are calculated values.
Figure 1: Calculation Method for the 2D-PKA
Approximator
.
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
160

(condition 3) every 2D-PKA cell needs 3 addition, 6
subtraction, 3 multiplication and 3 division operation
times plus the time needed for the memory address
calculation and data fetching (delays due to memory
related operation are assume to be constant).
However, for the ANN this time varies with the size
of the network (considering an operation time of one
+or- operation time for every node and an operation
time of one *or/ operation for each link). Therefore
the PKA in the forward execution is expected to be
faster than medium or large size ANN. Of course the
actual difference depends on the specific ANN and
needs to be quantified for each individual case. As
an example, a fully connected and biased ANN with
the 2:11:15:1 structure can be considered for
comparison where 229 multiplication operations and
202 (2-input addition) operations are required
(Kabiri, 1999).
Approximator has three levels of precision. As
explained above, accuracy in the first condition is
100%. The second and the third conditions
respectively have less accuracy. The amount of error
in the two latter conditions depends on the closeness
of the graph between two sample points to the
straight line. The amount of error in those conditions
also relates to the distance between two sample
points. This means that the higher the resolution, the
more accurate is the approximation. There is no
training stage for this approach and it is ready as
soon as all the samples become accessible to the
Approximator (Loaded into the memory). Despite
the complexity of the pattern introduced to the PKA,
one PKA cell is sufficient for learning the pattern.
Another feature for this method is the possibility to
update the knowledge of the PKA while using it.
This is because the database generated by the
method (tabular data), enables us to accurately
locate any part of the knowledge and change it.
5 RESULTS
In order to perform a numerical comparison between
the PKA and the ANN methodologies an experiment
is prepared. In this experiment the data derived from
an equation is used as a frame of reference and the
methodologies were compared with respect to this
frame of reference. In the following, the experiment
is described and results are presented.
5.1 System Variables
As it is described in section 4 the accuracy for the
PKA in sampled points is 100%. Therefore, the
Maximum Error and the Mean Square Error (MSE)
for the PKA at the sampled points are zero. In order
to compare the PKA with the ANN method the
following experiment was designed and
implemented (Kabiri, 1999).
This experiment is aimed to help both in
comparing the important features in the hypothesis
surfaces of these methods and their resultant error
values. These methods (ANN and PKA) will be
compared with respect to the error values resulting
in the sampled points, interim points and finally all
together. In order to do the comparison, function
()
(
)
22
22
sin*0.100
,
vu
vu
vuSINC
+
+
=
was selected as the
frame of reference for the comparison, because it is
sufficiently complex to include a range of angular
variations from very sharp to gently curved patterns.
The properties of this function are analysed to
provide a better form of comparison. The original
domain of the
()
vuSINC ,
function is
[]
2/2/,
ππ
−∈vu
. The input domains for the
function are moved to
[]
0.2450.110∈x
and
[]
0.900.90−∈y
in the scale of millimetres. The
maximum value for the function is 100.0mm. Using
this function, a sample dataset was produced in
equal sampling steps of 3.0mm for the x-axis and
9.0mm for the y-axis. The ANN was trained using
the generated dataset. As the PKA method has no
training stage, it uses this dataset for the
generalisation.
In order to generate the generalised dataset, the
sampling step for the x and y-axes were respectively
altered to 1.0mm and 3.0mm. In other words the
resolutions for the axes are increased by the factor of
3. The total number of samples introduced to both
methods is 966 samples. As the result of the
generalisation, the population of the sampled dataset
increases to 8296 samples. The following describes
Condition 1
Condition 1
Condition 2
2D-PKA
Top Layer
2D-PKA
Bottom Layer
Figure 2: Methodology for the 3D-PKA Calculations.
1. Simpler operation means shorter execution time for the operation.
A COMPARISON BETWEEN THE PROPORTIONAL KEEN APPROXIMATOR AND THE NEURAL NETWORKS
LEARNING METHODS
161
the training parameters of the ANN.
The ANN consists from a fully connected and
biased with 2 layers network structure of 2:11:15:1.
The training for the ANN was carried out on a
Pentium-400 based PC. Learning rate was initially
equal to 0.9 and later it was changed to 0.7, 0.5, 0.3,
0.2 and 0.1. Momentum factor for the training was
0.9 and was later changed to 0.8 and finally 0.7. The
training was many times forced to restart again. This
was because of different reasons such as need for
more nodes in the network, over training or lack of
progress in the training. The training process took
around 10 days. In the final reported training, the
total number of elapsed epochs was 1382755
epochs. Total training time was 285899.0 seconds
(3 days, 7 hours, 24 minutes and 59 seconds). The
final MSE using normalised data on the output was
0.00027 and the final MSE using de-normalised (in
order to make it comparable with the PKA values)
data on the output was 6.04.
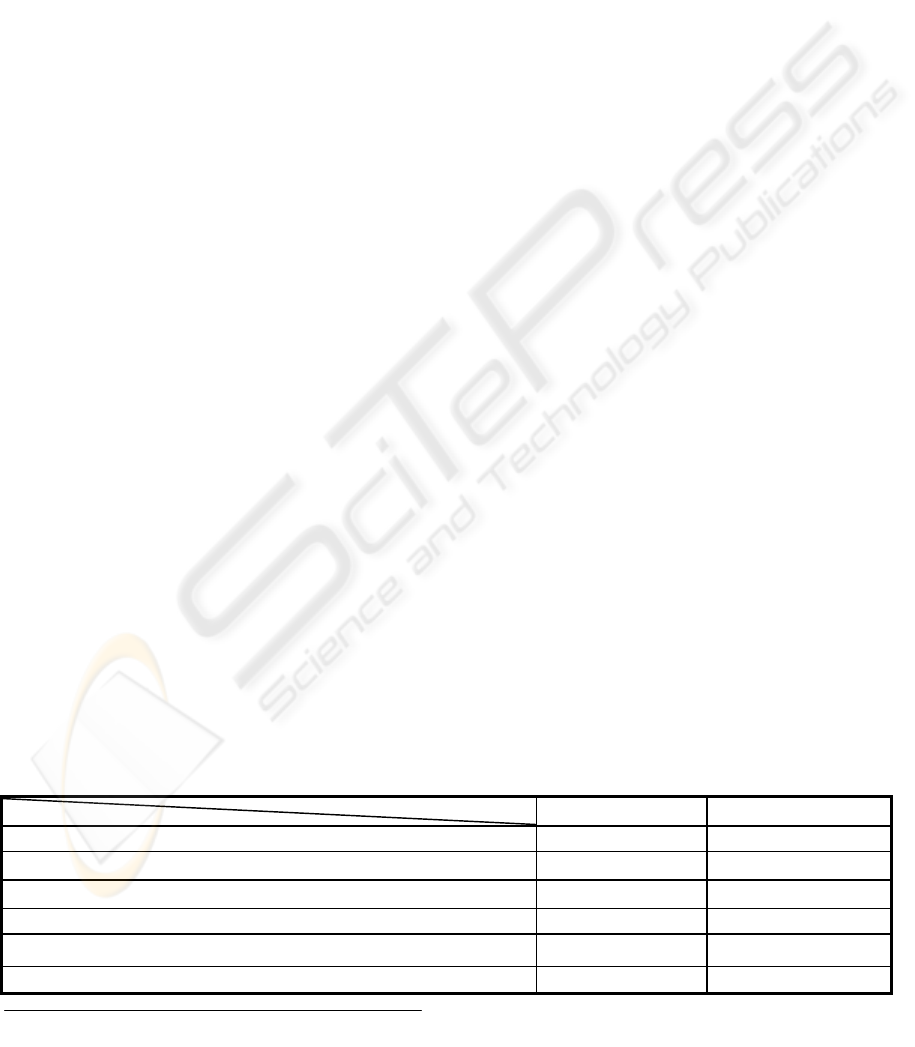
Table 1 compares two methods. In this table by
the term “the whole generalised points” the author
means the sampled points plus the generalised
interim points. Figure 4-a to Figure 4-c respectively
depict the output from the reference equation, PKA
and ANN. In Figure 3-a to Figure 3-c the
aforementioned dataset is generalised using
respectively the reference equation, PKA and ANN.
In analysing the data it is important to
understand that in any estimation the size of the
sampling step plays an important role in the final
resulting estimation error. If the speed of change in
the dataset is very high then a small sampling step is
required. This is some how the case in this example.
The ratio of the rise in the height of the graph is
sometimes too fast for the applied sampling step
size. Figure 5 depicts this concept.
As it can be seen in Figure 5-a, in the PKA
method the error values are higher at the centre of
the function domain than the rest of the points. In the
PKA method, the error is not evenly distributed in
the function domain. In this example in the PKA
method, although the maximum error seems to be
higher than the ANN method (Figure 5-b), most of
the points are well below the MSE value.
Figure 5-b depicts the distribution of the error
values in the ANN method. This figure shows that
the ANN method has a more evenly distributed error
pattern than the PKA method. However most of the
error values in this method are close to its MSE.
5.2 Analysis of the Result
Analysing the result, first the differences can be
divided into two categories training stage and the
execution stage. Later both of these categories will
be divided into smaller subsets such as difference in
execution speed, accuracy and some differences due
to the properties of the PKA methodology.
In the training stage as it is for the ANN, the
difference is huge. No training for the PKA in
comparison to the 3 days training for the ANN is a
clear advantage for the PKA methodology. Contrary
to the ANN that the required time for the training
can be different from one dataset to another, the time
required for the PKA to learn knowledge (the
training stage) is always the same. This property
plus ability to update the knowledge during the
execution are two of the main advantages of the
PKA. On the other hand PKA requires a large
memory to hold the samples that makes it a
memory-bound process, the fully connected and
biased ANN using the BP model is mostly a CPU-
bound process. Currently cost of the CPU time and
the Memory module are falling.
Sensitivity to the complexity in the training
pattern and sample population affects the training
stage for the ANN and in the supervised training it
might be necessary to reorganise the network and
restart the training. However, in the PKA none of
these problems will be encountered. After the
training for the ANN using extra sample points the
result has to be verified, but in the PKA due to the
consistency in the linear approximation this is not
necessary. In the reported experiment maximum
error in the PKA method was larger than the ANN
method. This difference is due to the large
Table
1
: A numerical comparison between the PKA and the ANN. All the values are in millimetres
.
(MSE is
calculated using de-normalised data values). (*) Means that: Where output should be 91.98 it was 78.95
The ANN The PKA
Maximum
3
error for the sampled points. 1.3 0.0
MSE for the sampled points. 6.0 0.0
Maximum error (difference) for the interim points. 8.7 13.0 (*)
MSE for the interim points. 9.0 4.1
Maximum error (difference) for the whole generalised points. 8.7 13.0 (*)
MSE for the whole generalised points. 8.0 3.6
3
. Maximum error is a relati
ve error (between the reference
value and the generalised value.
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
162

non-linearity in the hypothesis space at that point
and low sampling step.
This result may change for other curves and it is
an uncertain region for both methods. Nevertheless
this problem is the subject for further research to
implement the PKA method in the Spherical or
Cylindrical co-ordinate systems. In training the
ANN any randomly collected sample data is
acceptable, but the PKA method can only work with
tabulated dataset collected with equal sampling
steps. This is a major drawback for this method, but
the reader has to note that in the industry tabulated
data sampling is the most common method. The
requirement for the tabulated data makes the PKA
not suitable for the biological kind of research
activities that may need to use randomly collected
data. Possibility of using the random sampled data
for the PKA is also a research subject that is under
investigation.
The execution speed of the ANN is dependent on
the organization of the network and the number of
nodes and links in the network. However, the
execution time for the PKA has a maximum delay
condition (Condition 3, section 2 for the 2D-PKA
and section 3); this is because only one cell is
sufficient to learn any complex pattern in the dataset.
150
200
-50
0
50
0
50
X Axis
Y Ax
Z Axis
a) The original sampled d
ataset with 3 times higher
sample resolution in either of the axes.
150
200
-50
0
50
0
50
X Axis
Y Axis
Z Axis
b)
The output from the PKA with 3 times higher
sample resolution in either of the axes.
150
200
-50
0
50
0
50
X Axis
Y Ax
Z Axis
c) The output from the ANN with 3
times higher
sample resolution in either of the axes.
Figure 3: A comparison between the original sampled
dataset and the resulted output from both PKA and ANN
methods with generalisation (X*3, Y*3). The z-axis
represents the output.
150
200
-50
0
50
0
50
X Axis
Y Axis
Z Axis
a) The original sampled dataset (X*1, Y*1).
150
200
-50
0
50
0
50
X Axis
Y Axis
Z Axis
b) The output from the PKA with no generalisation.
150
200
-50
0
50
0
50
X Axis
Y Axis
Z Axis
c) The output from the ANN with no generalisation.
Figure 4: A comparison between the Original sampled
dataset and the resulted output from the both PKA and
ANN methods without any generalisation (X*1, Y*1).
The z-axis represents the output.
()
(
)
22
22
sin*0.100
,
vu
vu
vuSINC
+
+
=
A COMPARISON BETWEEN THE PROPORTIONAL KEEN APPROXIMATOR AND THE NEURAL NETWORKS
LEARNING METHODS
163

Execution time for large and medium size ANN is
longer than the PKA (section 4).
6 CONCLUSIONS
In comparing the PKA and the ANN methodologies,
before deriving any conclusions the reader should be
reminded that in this paper a young (4 years old)
method i.e. PKA has been compared with a well
established method such as the ANN. Therefore,
expectation should be as far as a 4 years old
methodology and one should just consider this
comparison as an introduction to potentials of a new
methodology (PKA) and in no way as a mean of
disregarding the ANN. For the PKA there is still a
long way to go to reach maturity in concept as it has
been achieved for the ANN.
This paper highlights the differences between the
PKA and the ANN methodologies and compares
some limitations of one versus advantages of the
other. In this report only a 2D-PKA in Cartesian co-
ordinates is compared with back propagation type of
the ANN with 2 inputs and 1 output. In both
methodologies sampling resolution plays a major
role in the accuracy of the estimation. In some areas
such as the training process, execution speed and
accuracy the 2D-PKA shows some advantages over
the ANN. On the other hand the ANN has some of
its own properties such as the ability to learn
randomly collected dataset, which the 2D-PKA is
not yet capable of performing. As a young
methodology the PKA still needs more research to
be done to extend its methodology and to find more
about its properties. New generations of the PKA in
Cylindrical and Spherical co-ordinate systems are
expected to provide us with new features and better
accuracy for the estimation of the curved patterns.
REFERENCES
Kabiri, P., 2002. Using Black Box and Machine Learning
Approach in Controlling a Machine. In SMC’02, 2002
IEEE International Conference on Systems, Man and
Cybernetics. IEEE.
Kabiri, P., Sherkat, N. and Shih, V.,1999. Compensating
for Robot Arm Positioning Inaccuracy in 3D-Space, In
SPIE's International Symposium on Intelligent Systems
in Design and Manufacturing II, SPIE.
Kabiri, P., Sherkat, N. and Shih, V.,1998. Compensation
for Robot Arm Flexibility Using Machine Intelligence,
In SPIE's International Symposium on Intelligent
Systems in Design and Manufacturing, SPIE.
Mingzhong, L. and Fuli W., 1997. Adaptive Control of
Black-Box Non-Linear Systems Using Recurrent
Neural Networks, In Proceedings of the 36th IEEE
Conference on Decision and Control, IEEE.
McLauchlan, R. A., Ngamsom, P., Challoo, R. and
Omar S. I., 1997, Three-Link Planar Robotic Arm
Trajectory Planning and Its Adaptive Fuzzy Logic
Control, In IEEE International Conference on Systems
Man and Cybernetics, IEEE.
Sima, J., 1996. Back-propagation is not efficient, In
Neural Networks Journal.
Chen, J. and Chao, L. M., 1986. Positioning Error
Analysis for Robot Manipulators with All Rotary
Joints, Proceedings of IEEE International Conference
on Robotics and Automation, IEEE.
Schaal, S. and Atkeson, C. G., 1994. Robot
Joggling: Implementation of Memory Based
Learning, In IEEE Control Systems, IEEE.
0
50
100
150
-250
-200
-150
-100
0
1
2
3
4
5
6
7
8
X A x is
Y Axis
Z Axis
0
50
100
150
-250
-200
-150
-10
0
5
10
X Axis
Y Ax
Z Axis
The distribution of the error for the ANN The distribution of the error for the PKA
Figure 5: A comparison for the resultant error between the original sampled dataset and the resulted output from the both
PKA and ANN methods with generalisation (X*3, Y*3). The z-axis represents the difference between the output from the
reference equation (SINC) and the output produced by each method.
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
164
