
FUZZY MULTIPLE-LEVEL SEQUENTIAL PATTERNS
DISCOVERY FROM CUSTOMER TRANSACTION DATABASES
An Chen
Institute of Policy and Management, Chinese Academy of Sciences
Beijing, 100080, P. R. China
Huilin Ye
School of Electrical Engineering and Computer Science
University of Newcastle, 2308, Australia
Keywords: Data mining, Fuzzy sequential
patterns, Transaction databases
Abstract: Sequential pattern discover
y is a very important research topic in data mining and knowledge discovery and
has been widely applied in business analysis. Previous works were focused on mining sequential patterns at
a single concept level based on definite and accurate concept which may not be concise and meaningful
enough for human experts to easily obtain nontrivial knowledge from the rules discovered. In this paper, we
introduce concept hierarchies firstly, and then discuss a mining algorithm F-MLSPDA for discovering
multiple-level sequential patterns with quantitative attribute based on fuzzy partitions.
1 INTRODUCTION
Data mining is a process of nontrivial extraction of
implicit, previously unknown and potentially useful
information from databases (Chen et al., 1996). The
discovered knowledge can be applied to information
management, query processing, decision making,
process control, and many other applications (Chen
et al., 2001).
Discovering sequential patterns and association
rul
es from customer transaction databases is an
important topic of data mining. Since Agrawal et al.
(1993) first introduced the problem of discovering
sequential patterns and association rules between
items over basket databases there has been
considerable work devoted to the algorithms for
mining sequential patterns and association rules
(Agrawal and Srikant, 1994, Park et al., 1995). Like
time series in statistics, sequential data can often be
found in real databases. For example, in a customer
transaction database, data records often contain
customer information (for example, customer-id,
transaction time, purchased items and quantity etc),
particularly when the purchase has been made using
a credit card or a bank card. It is useful to find the
sequential patterns that most frequently occur in
customer transaction databases to find some rules of
the purchases. For example, in an electronic
appliance market, if many customers bought TV,
followed by DVD player, and followed by Movies
in one month in a transaction database, then <TV,
DVD, Movies> is a sequential pattern with large
possibility.
A customer transaction database records the
ite
ms purchased by the customers. Usually these
items can be organized into a concept hierarchy
according to a given taxonomy. Based on the
hierarchy, association patterns can be found not only
from the leaf nodes (i.e. the purchased items) of the
hierarchy, but also can be found at any level of the
hierarchy. This is called multiple-level sequential
patterns discovery, or mining generalized
association patterns (Srikant and Agrawal, 1995).
Previous work has been focused on mining
sequential patterns at a single concept level
(Agrawal and Srikant, 1995, Chen and Chen, 1999).
Now the necessity for mining multiple-level
association patterns using concept hierarchies has
been observed as finding sequential patterns at
multiple concept levels is useful in many
434
Chen A. and Ye H. (2004).
FUZZY MULTIPLE-LEVEL SEQUENTIAL PATTERNS DISCOVERY FROM CUSTOMER TRANSACTION DATABASES.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 434-440
DOI: 10.5220/0002608604340440
Copyright
c
SciTePress

applications. The sequential patterns at lower
concept levels often carry more specific and
concrete information and those at higher concept
levels carry more general information. This requires
progressively deepening the mining process to
multiple concept levels. In many cases, concept
hierarchies over items are available. Given a set of
transactions and a concept hierarchy over items
contained in the transactions, association patterns at
any level of the hierarchy can be found by
developing appropriate algorithms (Chen et al.,
2001).
Quantitative association rules over a set of
purchased items in a customer transaction database
were defined over quantitative and categorical
attributes of the items (Srikant and Agrawal, 1996).
The values of categorical attributes were mapped to
a set of contiguous integers. While the domain of
quantitative attributes was discretized into intervals
by fine-partitioning the values of the attributes and
combining the adjacent partitions as necessary and
the intervals were then mapped to contiguous
integers. As a result, each attribute had a form of
<attribute, value> where value was the mapped
integer of an interval for quantitative attributes or a
single value for categorical attributes. Then the
algorithms for finding Boolean association rules can
be used on the transformed database to discover
quantitative association rules. Some algorithms have
been proposed (Agrawal and Srikant, 1995, Chen et
al. 2001, Agrawal and Srikant, 1994). But, few of
them focused on quantitative sequential patterns that
involves discretising the domain of quantitative
attributes into intervals while these intervals may
not be concise and meaningful enough for human
experts to easily obtain nontrivial knowledge from
those rules discovered.
In this study, we present an algorithm for
mining sequential patterns at multiple levels with
quantitative attributes. Instead of using the partition
method discussed above, the fuzzy concept was
introduced into the algorithm. Fuzzy sets were
proposed by Zadeh (1965). Since then much
progress in theory and application of fuzzy sets has
been observed (Chen et al., 2001). The fuzzy
concept is considered better than the partition
method as fuzzy sets provide a smooth transition
between member and non-member of a set. The use
of fuzzy techniques makes the algorithms resilient
to noise and missing values in the databases. Fuzzy
concepts are not confined to a single attribute.
Instead, they can be defined on a set of attributes.
The proposed method for mining fuzzy
multiple-level sequential patterns uses a
hierarchically encoded customer-sequence table,
instead of the original customer transaction table.
The problem of mining multiple-level sequential
patterns with quantitative attributes can be split into
four steps:
(1) Transforming the original database into a
hierarchically encoded customer-sequences table;
(2) Fuzzy partitioning in each quantitative
attribute on each concept level;
(3) Finding all fuzzy large sequences at every
concept level using a top-down, progressively
deepening mining process;
(4) Generating all fuzzy sequential patterns and
sequential rules from the result of step 3.
Step 3 is the most crucial step for the method. As
long as all the fuzzy large sequences at each concept
level can be discovered, it is not difficult to derive
the corresponding sequential patterns and
association rules.
The paper is organized as follows. Section 2
introduces some related concepts of multiple-level
sequential patterns and fuzzy partitions of the
quantitative attributes. Based on these concepts the
problem of mining fuzzy multiple-level sequential
patterns can be formally characterized. Section 3
describes the method for mining fuzzy multiple-
level sequential patterns in detail. An algorithm for
discovering large sequences at each concept level is
presented and discussed. Section 4 concludes this
study.
2 PROBLEM STATEMENT
In a given customer transactions database D, each
transaction consists of the following fields:
customer-id, transaction-time, and the items
purchased in the transaction. No customer has more
than one transaction at the same transaction-time.
Each item is a binary variable representing whether
an item was bought or not. Let I = {i
1
, i
2
, …, i
n
} be a
set of literals. An itemset is a non-empty set of
items. A sequence is a non-empty and ordered list of
itemsets. We denote an itemset by (i
1
, i
2
, …, i
m
),
where i
j
is an item. The length of an itemset is the
number of items in it. An itemset of length k is
called a k-itemset. We denote a sequence S by <s
1
,
s
2
, …, s
n
>, where s
j
is an itemset. The length of a
sequence is the number of itemsets in it. A sequence
of length k is called a k-sequence. The sequence
formed by the concatenation of two sequences A and
B is denoted as <A, B>. The following concept
definitions are based on (Agrawal and Srikant,
1995, Chen et al. 2001).
Definition 1: All the transactions of a customer
can together be viewed as a sequence, where each
transaction corresponds to a set of items, and the list
of transactions, ordered by increasing transaction-
time, corresponds to a sequence. A transaction made
FUZZY MULTIPLE-LEVEL SEQUENTIAL PATTERNS DISCOVERY FROM CUSTOMER TRANSACTION
DATABASES
435
at transaction-time T
i
can be denoted as itemset (T
i
).
Thus, the sequence of the transactions made by a
customer, ordered by increasing transaction-time T
1
,
T
2
, …, T
n
, can be denoted by <itemset (T
1
), itemset
(T
2
), …, itemset (T
n
)> which is called customer-
sequence.
Definition 2: An itemset X is contained in a
transaction T if X ⊆ T. A sequence A = <a
1
, a
2
, …,
a
m
> is contained in another sequence B = <b
1
, b
2
, …,
b
n
> (i.e., A is a subsequence of B) if there exist
integers i
1
< i
2
< … < i
m
such that a
1
⊆ b
i1
, a
2
⊆ b
i2
,
…, a
m
⊆ b
im
. In a set of sequences, a sequence S is
maximal if S is not contained in any sequences in
the set.
Definition 3: A customer supports an itemset X
if X is contained in at least one transaction of the
customer-sequence for this customer. The support
for X is defined as the fraction of total customers
who support X. The support count for X, denoted by
X.support, is defined as the number of customers
who support X. A customer supports a sequence S if
S is contained in the customer-sequence for this
customer. The support for S is defined as the
fraction of total customers who support S. The
support count for S, denoted by S.support, is defined
as the number of customers who support S.
Definition 4 : This definition is based on fuzzy
set theory. The definition of membership functions
of fuzzy set and fuzzy patterns can be seen in
(Zadeh, 1965, Chen et al., 2001). Given a customer
sequence C = <d
1
, d
2
, …, d
n
> ⊆ D and a fuzzy
sequence S = <X
1
, X
2
, …, X
m
>, the membership of C
with respect to S is defined as
Since 0 ≤
µ
xj
(d) ≤ 1, then 0≤ µ
S
(C) ≤ 1.
Specially, for a fuzzy pattern X, the membership of
C with respect to X is defined as µ
X
(C)= max µ
X
(d
i
)
(1≤ i ≤ n).
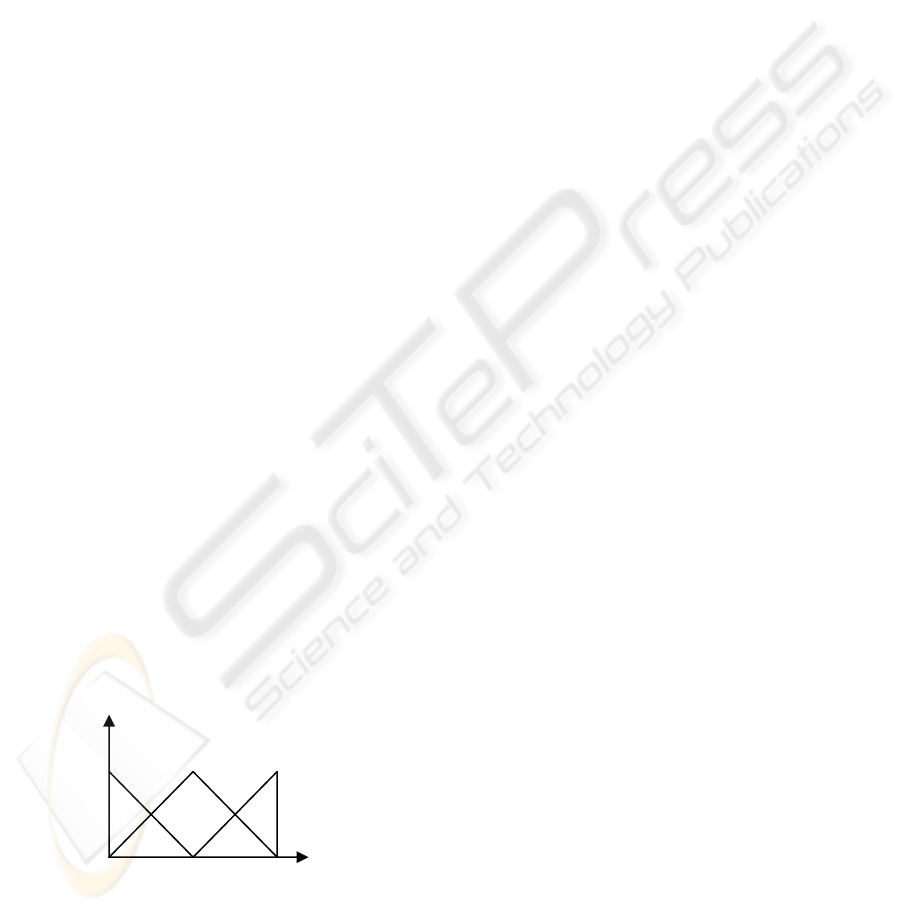
The example of fuzzy k-partitions (k = 3) can be
seen in figure 1.
Figure 1: Example of fuzzy k-Partition (k=3).
Definition 5: The support for a fuzzy sequence
S, called F-Sup(S), is defined as the fraction of the
sum of membership grades for all customer-
sequences with respect to S over the total number of
customers in D:
F-Sup(S) = ∑ (µ
S
(C) | µ
C
(d) ≥ ε) / (number of
customers in D)
Since for each customer sequence C ⊆ D,
0≤
µ
S
(C) ≤1, then 0≤ F-Sup(S) ≤1. A fuzzy
sequence S is large if its fuzzy support is not less
than a pre-defined support threshold, Fmin-sup.
Definition 6: A concept hierarchy is a tree
describing the relation of the concepts from the most
generalized level concept to primitive level. Each
node in the tree represents a concept and an edge
represents an is-a relationship between two
concepts. The root, called the first level of the tree,
is the most generalized concept and the leaves,
called the last level of the tree, are the most concrete
concepts. Let x and y be nodes in the concept tree. If
there is path from x to y, we call x an ancestor of y
or y a descendant of x. If x is the nearest ancestor of
y (i.e., there is an edge directly from x to y), we call
x a parent of y or y a child of x. Concept hierarchies
are given by domain experts and stored in the
database or automatically produced by the system.
An example of the concept hierarchy and how to
encode it can be found in the next section.
Definition 7: Different minimum fuzzy support
and confidence can be specified at different levels
for finding fuzzy multiple-level sequential patterns
and rules. Let F-minsup[p] be the minimum fuzzy
support count at level p, an itemset X is large at
level p if X.support≥ minsup[p]. Large itemset is
also called Litemset. Similarly, a fuzzy sequence S
is large at level p if S.support≥ F-minsup[p]. Since
each itemset in a large sequence must have
minimum support, any large sequence must be a list
of Litemsets. A fuzzy sequence patterns is the
maximal fuzzy sequences in the set of large
sequences.
)(minmax)(
,...,1
...1
21
jj
m
iX
mj
niii
S
dC
µ
µ
=
≤<<<≤
=
Definition 8: A fuzzy sequential rule is an
implication of the form F(A ⇒ B), where A and B are
sequences; the support count of the rule is
F(<A, B>.support).
It is defined as the number of customers who
support <A, B>. The confidence of the rule is
defined as F(<A, B>.support / A.support).
Confidence denotes the strength of implication and
support indicates the occurring frequency of the
rule. Let minconf[p] be the minimum fuzzy
confidence at level p. A fuzzy sequential rule at
level p is strong if the fuzzy support and fuzzy
confidence of the rule is not less than minsup[p] and
minconf[p] respectively.
1
Some concepts of single-level sequential
patterns defined above can be extended to multiple-
level sequential patterns.
Definition 9: An item x is contained in an
itemset X if x ∊ X or x’∊ X, where x’ is a descendant
0
c/2
c
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
436
of x, i.e. x is in X and x is an ancestor of some items
in X. An itemset X is contained in another itemset Y
if every item of X is contained in Y. A sequence A =
<a
1
, a
2
,…, a
m
> is contained in another sequence B =
<b
1
, b
2
,…, b
n
>, if there exist a set of integers i
1
< i
2
<
…< i
m
, such that a
j
contained in b
ij
.
Definition 10: An itemset X’ is an ancestor of
another itemset X if we can get X’ from X by
replacing one or more items in X with their
ancestors and deleting the identical items. A
sequence S’ = <y
1
, …, y
m
> is an ancestor of another
sequence S=<x
1
, …, x
m
> if for k = 1, …, m, y
k
= x
k
or
y
k
is an ancestor of x
k
and S and S’ have the same
length.
Some properties can be reached based on the
above definitions and set theory.
Property 1: If an itemset Y contains another
itemset X, then Y also contains Z where Z is an
ancestor of X.
Property 2: If a sequence B contains a
sequence A, then B also contains C where C is an
ancestor of A.
Property 3: If X is a large itemset, then its
ancestor X’ is also large.
Property 4: If S is a large sequence, then its
ancestor S’ is also large.
Based on the above concept definitions, the
problem of mining multiple-level sequential patterns
can be characterized as follows:
Problem Statement: Given a customer
transactions database D with quantitative attributes
and a concept hierarchy, the problem of mining
fuzzy multiple-level sequential patterns is to
discover all maximal sequences that have fuzzy
support not less than the user-specified minimum
fuzzy support at the corresponding level of the
concept hierarchy. Based on the discovered fuzzy
multiple-level sequential patterns, the fuzzy
sequential rules that have support and confidence
not less than the user-specified minimum fuzzy
support and minimum confidence at the
corresponding level can be found as well.
3 MINING FUZZY MULTIPLE-
LEVEL SEQUENTIAL
PATTERNS
In this section, we present a method of mining fuzzy
multiple-level sequential patters from large
customer transaction databases. As specified in
Section 1, this method consists of 4 major steps.
Each step is described in the following sub-sections.
3.1 Transfoming a Database into a
Encoded Customer-Sequence
Table
The proposed method for mining fuzzy multiple-
level sequential patterns uses a hierarchically
encoded customer-sequence table rather than the
original customer transaction table. The encoding of
a concept hierarchy will be discussed first and then
the method of transformation of a database to an
encoded customer-sequence table will be specified.
3.1.1 Coding a concept hierarchy
A customer transaction database records the items
purchased by the customers. Usually these items can
be organized into a concept hierarchy. Each leaf
node in a hierarchy represents an item and the items
can be classified into categories from more general
levels to more specific levels. We code each node in
a concept hierarchy using a top-down coding
method starting from the root and gradually down to
the leaves. The root of a hierarchy is coded first by
being assigned an integer of zero. For a hierarchy of
m levels, any non-root node in the hierarchy can be
coded based on the following formula:
code (p, i) = COP (p, i) x 10 + i
where p (p = 0, 1, …, m-1) represents the level
where the node resides; i (i = 1, 2, …, number of
nodes at level p) is the location number of a node at
level p, (a set of contiguous integers starting from 1
is assigned to the nodes from left to right as location
number); the code (p, i) denotes the code for the i
th
node at level p, COP (p, i) is the code of the parent
of the i
th
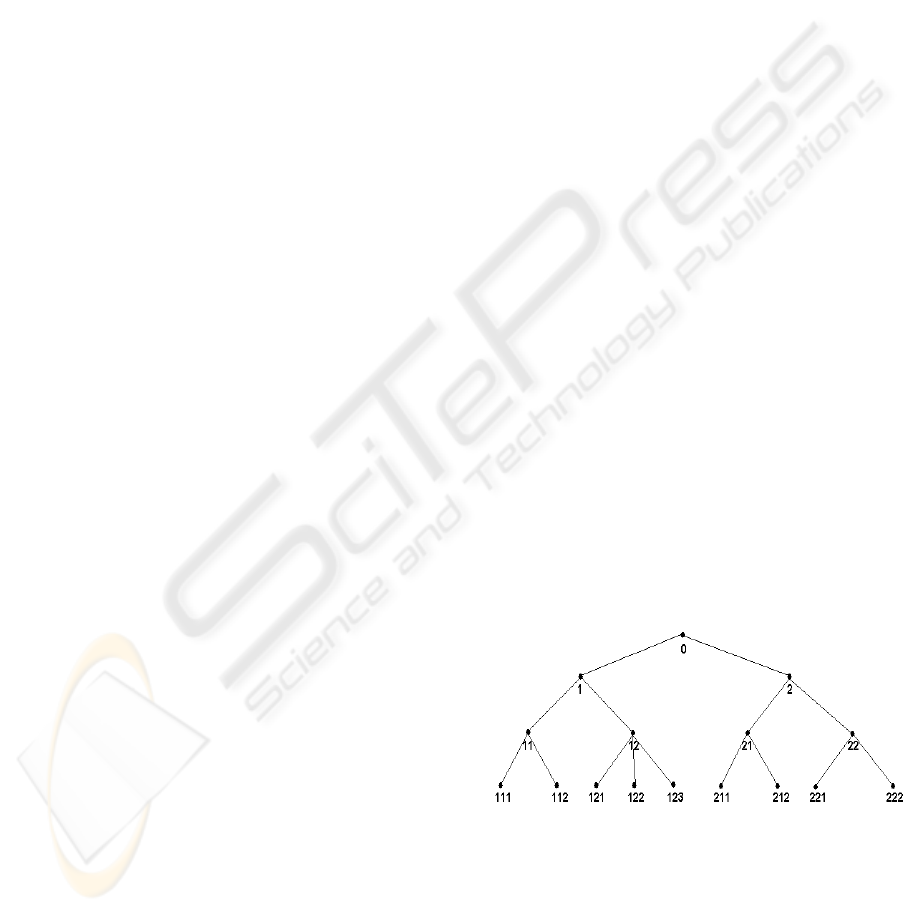
node at level p. An example of a hierarchy
and the code for each node are shown in Figure 1.
After the coding, each item recorded in a customer
transaction database will be represented by its code.
Figure 2: An example of concept hierarchy.
3.1.2 Sorting customer transaction database
A customer transaction database D can be sorted
with customer-id as the major key and transaction-
time as the minor key. After the sorting, all the
records having the same customer-id and increased
transaction-time can be converted to a customer-
FUZZY MULTIPLE-LEVEL SEQUENTIAL PATTERNS DISCOVERY FROM CUSTOMER TRANSACTION
DATABASES
437

sequence. Thus the original customer transaction
database can be converted to a customer sequence
table Ds.
3.2 Fuzzy Partitioning for Each
Quantitative Attributes
At each level of the concept hierarchy in transaction
database D, divide a quantitative attribute into
different categories according to a k-fuzzy partition,
where the value of k should be decided by the user;
a value of 3 is suggested. For example, the
purchased amount of a certain item is considered as
small, middle, or large will depend on a k-fuzzy
partition. For this example, as shown in Figure 1, c
will be the maximum value or a little bigger than
that of the purchase amount at a certain concept
level. Based on the partition, for a specific
purchased item amount at the lowest level (leaf
level) of a concept hierarchy, you will know the
amount of the purchase is small, middle, or large.
For a non-leaf node in a concept hierarchy, the
purchased amount will be the sum of the amount
purchased by its child-nodes.
After the encoding and fuzzy partition, each
item purchased in a transaction can be described by
its code and fuzzy value of the purchased amount,
such as 111-large.
3.3 Finding all Fuzzy Large Sequences
at Each Concept Level
Mining sequential patterns is based on mining large
itemsets which can be applied to association rule
discovery algorithms as its sub-functions. The
general structure is that they make multiple passes
over the database. In each pass, the new potentially
large sequences called candidate sequences are
generated from the large sequences obtained in the
previous pass. Their supports are calculated during
the pass of the database and the actual large
sequences are obtained.
Firstly, we select all the large sequences for
each concept level based on the pre-defined
minimum support. Then, we check each large
sequence with the fuzzy partitions if it is also larger
than the fuzzy support. If both conditions are
satisfied the sequence will be selected as a large
sequence. Therefore the algorithm for finding all the
large sequences for each concept level based on the
pre-defined minimum support is crucial. An
algorithm, called MLSeq_T2L1 is shown in Figure
3 which is an extension of ML_T2L1 algorithm
(Han and Fu, 1995]. The major variables used in
the algorithm and their semantics are listed in Table
1.
The inputs of the algorithm are:
(1) T[1]: a customer-sequence table (encoded
based on a concept hierarchy)
(2) minimum support thresholds minsup[p] and
Fminsup[p] for each concept level p.
The output of the algorithm will be the large
sequences LL[p] at every level p. The algorithm
describes the process of how to generate the large
sequences LL[p] for all levels (p =1, 2, …,
max_level).
This algorithm consists of two parts: (a)
generating large itemsets, and (b) generating large
sequences based on the identified large itemsets.
During this process, some intermediate tables will
also be derived. At any level p, large k-itemsets
(k=1, 2, …, n) L[p] is derived from T[p] by invoking
get_large_itemset(T[p], p) function (see Statement
(1) and (3) of the algorithm). The filtered customer-
sequence table T[p+1] can be derived by invoking
get_filtered_table (T[p], L[p, 1]) function, which
uses L[p, 1] as a filter to filter any small items from
customer-sequences and to remove the sequences
that contain only small items from T[p] (see
Statement (2)).
.
Table 1: Notations used in MLSeq_T2L1
Variable Description
L [p, k] Set of large k-itemsets at level p
Each member of this set has two fields: (i) itemset and (ii) support count
C [p, k] Set of candidate k-itemsets at level p
L [p] Set of all large itemsets at level p, L[p]= ⋃
k
L[p, k] (k=1, ..., n, where n is the
maximum length of large itemsets at level p)
LL [p, k] Set of large k-sequences at level p
Each member of this set has two fields: (i) sequence and (ii) support count
CL [p, k] Set of candidate k-sequences at level p
LL [p] Set of all large sequences at level p, LL [p]= ⋃
k
LL [p, k] (k=1, ..., n, where n is the
maximum length of large sequences at level p)
T [p] Filtered customer-sequence table derived from L [p-1, 1] at level p-1
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
438

(0) L[1] = get_large_itemset (T[1], 1);
(1) for (p:=1; L[p,1] <> ∅ and p <= max_level; p++) do
{ (2) T[p+1] = get_filtered_table (T[p], L[p, 1]);
(3) if (p>1) then
(3.1) L [p] = get_large_itemset (T[p], p);
(4) T’ = transform_table (T[p+1]);
(5) LL[p, 1] = { <iset> | iset∈ L[p] };
(6) for (k:=2; LL[p,k-1] <> ∅ ; k++) do
{
(6.1) CL[p,k] = get_candidate_set (LL[p,k-1]);
(6.2) for each t∈ T’ do
{
(6.3) C
t
= get_subsets (CL[p,k],t);
(6.4) for each c∈ C
t
do
(6.5) c.support ++;
}
(6.6)LL[p,k] := {c∈ CL[p,k]|c.support≥ minsup[p] and F-
sup(c) ≥Fminsup [P]}
}
(7)LL[p]:=⋃
k
LL[p,k];
}
Figure 3: Algorithm of MLSeq_T2L1.
In Statement (4), an intermediate table T’ at
level p is generated from the transformation from
the filtered table T[p+1]. This intermediate table
will be used to derive large sequences.
Large 1-sequences at any level LL[p, 1] can
be generated based on Statement (5) while large k-
sequences (k>1) at level p are derived in two steps
(see Statement (6) and its Sub-statements (6.1)-
(6.6)):
(a) The candidates of k-sequences are
generated from LL[p, k-1] by invoking
get_candidate_set (LL[p, k-1]) function. The
function takes LL[p, k-1]
as a parameter and
returns a set of all candidate k-sequences at level
p, CL[p, k].
(b) For each customer-sequence t in T’,
increment the support count of S ∈ CL[p, k] if S is
contained in t. Then LL[p,k] can be derived from
those sequences in CL[p, k] whose support and
fuzzy support are not less than minsup[p] and
Fminsup[p] respectively.
Finally, the large sequences at any level p,
LL[p], is the union of LL[p, k] for all k (see
Statement (7)).
3.4 Generating Fuzzy Sequential
Patterns and Sequential Rules
Having found the set of all large sequences LL[p]
(p = 1, 2, …, max-level), we can identify fuzzy
sequential patterns and rules.
(1) Fuzzy Sequential patterns (Maximal
sequences of large fuzzy sequences):
The following algorithm can be used for
finding maximal sequences. Let the length of the
longest sequence of LL[p] is n[p]. We delete the
non-maximal sequences which are contained in
other sequence of LL[p]:
maximal_seq()
{for (p := 1; p ≤ max_level; p++) do
for (k := n[p]; k ≥1; k --) do
for each k-large sequence S do
delete all subsequences of S
from LL[p]
}
Data structure and algorithm to quickly find
all subsequences of a given sequence are described
in (Agrawal and Srikant, 1994).
(2) Sequential rules
We also can use large sequences to generate
the desired sequential rules. For every large
sequence S at level p, find all non-empty prefix
subsequences of S. For every such subsequence A,
a rule is an implication of the form F(A⇒ B),
FUZZY MULTIPLE-LEVEL SEQUENTIAL PATTERNS DISCOVERY FROM CUSTOMER TRANSACTION
DATABASES
439

where <A, B> = S. A fuzzy sequential rule at level
p is strong if the fuzzy support and fuzzy
confidence of the rule is not less than minsup[p]
and minconf[p] respectively. We need to consider
all prefix subsequences of S to generate sequential
rules with corresponding consequences.
4 CONCLUSIONS
Mining sequential patterns is a meaningful task in
the research of data mining which can discover
implicit and potential useful knowledge from large
customer transaction databases. In this paper, we
introduce the problem of finding fuzzy multiple-
level sequential patterns with quantitative
attributes using concept hierarchies and fuzzy
concepts. An algorithm designed to solve this
problem is presented.
An experiment that applies the algorithm to a
real-life customer transaction database will be
conducted in the near future.
REFERENCES
Agrawal R., Imielinski T., and Swami A., 1993. Mining
association rules between sets of items in massive
databases. In
Proc. of the ACM-SIGMOD 1993 Int'l
Conference on Management of Data
, Washington
D.C, pp 207-216.
Agrawal R. And Srikant R., 1994. Fast algorithm for
mining association rules. In Proc. of 20
th
VLDB
conference, Santiago, Chile, pp 487-499.
Agrawal R. and Srikant R., 1995. Mining sequential
patterns. In Proc of the 11th int’l conference on data
Engineering, Taipei, Taiwan, pp 3-14.
Chen M., Han J., and Yu P., 1996. Data Mining: An
overview from a database Perspective. IEEE Trans
on Knowl and Data Eng, 1996; 6: 866-883.
Chen N., Chen A., Zhou L., and Liu L., 2001. A Fast
algorithm for mining sequential patterns from large
databases. Jour of Comp Sci and Tech 2001; 4:359-
370.
Chen N. and Chen A., 1999. Discovery of multiple-level
sequential patterns from large database. In Proc of
the 4
th
Int’l symposium on future software
technology (ISFST-1999). Nanjing, P. R. China,
pp169-174.
Chen R., Tzeng G., Chen C., and Hu Y., 2001. Discovery
of fuzzy sequential patterns for fuzzy partitions in
quantitative attributes. In Proc of ACS/IEEE int’l
conference on computer systems and applications
(AICCSA'01), Beirut, Lebanon, pp144-150.
Chen N., Chen A., and Zhou L., 2001. Efficient
algorithms for mining fuzzy rules in large
relational databases, Jour of Software 2001;
7:949-959.
Han J. and Fu J., 1995. Discovery of multiple
association rules from large Database. In Proc of
21
st
VLDB conference, Zurich, Switzerland, pp 420-
431.
Park J., Chen M. and Yu P., 1995. An effective hash
bashed Algorithm for mining association rules. In
Proc of ACM SIGMOD 1995, pp175-186.
Srikant R., and Agrawal R., 1995. Mining generalized
association rules. In Proc. of 21
st
VLDB conference,
Zurich, Switzerland, pp 407-419.
Srikant R., and Agrawal R., 1996. Mining quantitative
association rules in large relational tables. In Proc of
ACM SIGMOD, Montreal, Canada, pp1-12.
Zadeh, L., 1965. Fuzzy sets. Info Cont’l, 1965; 3:338-
353.
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
440
