MULTI-AGENT APPROACH BASED ON TABU SEARCH FOR

THE FLEXIBLE JOB SHOP SCHEDULING PROBLEM

Meriem Ennigrou

and Khaled Ghédira

1 ur. SOI²E, Stratégies d'Optimisation de l'Ingénierie des Informations et de la connaissancE

IPEIM, Institut Préparatoire aux Etudes d'Ingénieurs – ElManar, 2092 El Manar 2 BP 244, Tunisie

2 ur. SOI²E, Stratégies d'Optimisation de l'Ingénierie des Informations et de la connaissancE

ENSI, Ecole Nationale des Sciences de l'Informatique, 2010 Campus Universitaire la manouba, Tunisie

Keywords: Multi-Agent System, flexible Job Shop, Scheduling, Tabu Search

Abstract: This paper proposes a Multi-agent approach based on a tabu search method for solving the flexible Job Shop

scheduling problem. The characteristic of the latter problem is that one or several machines can process one

operation so that its processing time depends on the machine used. Such a generalization of the classical

problem makes it more and more difficult to solve. The objective is to minimize the makespan or the total

duration of the schedule. The proposed model is composed of three classes of agents: Job agents and

Resource agents which are responsible for the satisfaction of the constraints under their jurisdiction, and an

Interface agent containing the tabu search core. Different experimentations have been performed on

different benchmarks and results have been presented.

1 INTRODUCTION

Scheduling problems arise in several economic

fields and thereby play an important role in

production management. A scheduling problem

consists in allocating a set of jobs to a finite set of

resources over time while satisfying a set of

constraints.

Among the most difficult scheduling problems,

we find the Job Shop Scheduling Problem. Solving it

optimally seems to be very hard, in the majority of

cases, because of its high complexity. In fact, this

problem falls into the category of NP-hard problems

for which exact solving methods are inappropriate

since they explode with problem size. However,

approximate methods are more suitable for such

problems. The latter are based on local search

techniques such as tabu search or simulated

annealing or on evolutive techniques such as genetic

algorithms and ant systems.

In this paper we present a Multi-Agent model

based on the tabu search technique for solving the

flexible job shop scheduling problem. The latter

represents a generalisation of the classical problem

and is consequently more difficult to solve.

The paper is organised as follows: section 2

defines the problem subject of our research, the

following one presents the tabu search method on

which is based our model. Then, we describe the

Multi-Agent model proposed, its agents and its

global dynamic. Next, we present an illustrative

example. Finally, we give some experimental

results.

2 THE FLEXIBLE JOB SHOP

PROBLEM

A Job shop Scheduling problem consists in

performing a set of n jobs {J

, …, J

} on a set of m

resources {R

, …, R

}. Each job J

, i=1,…,n, is

composed of n

operations that must be performed

on the different resources according to a predefined

order, known as the job process routing. This one

characterizes the precedence constraints existing

between the operations of one job. In addition, each

operation has a processing time known in advance

and can be processed by only one resource.

Furthermore, each job has to be achieved in a

temporal range defined by its release date, before

which the job cannot be started, and its due date,

before which the job must be completed. This

temporal range defines the temporal constraints of

Ennigrou M. and Ghédira K. (2004).

MULTI-AGENT APPROACH BASED ON TABU SEARCH FOR THE FLEXIBLE JOB SHOP SCHEDULING PROBLEM.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 22-28

DOI: 10.5220/0002610000220028

 SciTePress

that job. Moreover, a resource can perform only one

operation at a time which correspond to the

disjunctive constraints, and an operation cannot be

interrupted unless it is finished, i.e. no pre-emption

is allowed. A solution for the job shop problem

consists in fixing a start time for each operation

satisfying the set of constraints.

The Flexible Job Shop Problem, first introduced

by Nuijten & Aarts (1996), is a generalisation of the

above mentioned problem, where each operation can

be processed by more than one resource and has

consequently a processing time depending on the

resource used. A solution consists then not only in

sequencing the operations on the resources and

fixing them a start time but also in allocating them to

a resource likely to achieve them. This problem is

also NP-hard.

Some approaches have been proposed for solving

it, they are based on the tabu search method. Among

them, the approach proposed by Mastrollili et

Gambrella (2000), Brucker & Neyer (1998),

Chambers & Barnes (1996).

3 TABU SEARCH

The model we propose in this article is based on the

tabu search method, Glover (1986), which is a meta-

heuristic based on the local search principle. The

latter consists in exploring the search space

composed of the set of solutions in order to find the

optimal one. More precisely, beginning from an

initial solution, it consists to choose, at each

iteration, the best solution in the current solution

neighbourhood, even if it does not improve the

quality of the solution. A neighbourhood is

composed of all the solutions obtained by a simple

move on the current solution. These solutions are

named, then, neighbours of the current solution.

In order to escape local optima in which the

system can be easily trapped, tabu search uses a

temporary memorisation structure in which it keeps

track of the last visited solutions: the tabu list. In

fact, a solution is forbidden during a number of

iterations equal to the tabu list size. Then, the best

solution among the ones not forbidden is selected for

the next iteration.

Although its efficiency in solving many difficult

problems, tabu search remains yet hardly adaptable

to flexible job shop problem because of the great

number of parameters to define:

– initial solution,

– neighbourhood function,

– evaluation of the current solution,

– tabu list size,…

In the following section, we describe briefly our

adaptation of the different parameters to the flexible

job shop. Subsequently, we present our multi-agent

model and its global dynamic.

3.1 Neighbourhood function

A tabu search based approach complexity depends

essentially on (1) the current solution neighbourhood

size and on (2) the evaluation scheme of this

neighbourhood with which the best solution will be

determined. Eikelder et al. (1997) have shown that

almost 90% of the solving time is consumed by

neighbourhood evaluation. Consequently, it seems

interesting to reduce the size of the neighbourhood

in order to reduce problem complexity.

To present our neighbourhood function, we need

first define the notion of critical path. A critical path

of a solution is the path which length is equal to the

schedule one and that is composed of operations

related to by either:

– a precedence constraint, or

– a disjunctive constraint (operations that can

be performed by the same resource)

A critical operation is an operation which

belongs to a critical path. the neighbourhood of a

solution is obtained by two types of moves:

1. Switch of two adjacent critical operations

achieved by the same resource.

2. Migration of a critical operation on another

potential resource.

3.2 Neighbourhood evaluation

The best non tabu neighbour belonging to the

current solution neighbourhood will be selected for

the next iteration. Hence, all neighbours must be

evaluated in order to determine the best one.

However, a global evaluation, i.e. computation of all

the start times of all the operations, of each

neighbour will need a considerable time. For this

reason, only a subset of operations will be taken into

account and to which start times will be redefined.

These operations are effectively concerned by the

move executed.

In the following, we define this sub-set of

operations in both cases of switch of two critical

operations and in the swap of a critical path on

another potential resource. We denote JS(O

) the

next operation of O

according to the process routing

of the job of O

. Similarly, we name MS(O

) the next

operation of O

performed on the same resource as

MULTI-AGENT APPROACH BASED ON TABU SEARCH FOR THE FLEXIBLE JOB SHOP SCHEDULING

PROBLEM

3.2.1 Switch of two critical operations

Let O

and O

be two critical operations performed

by resource R

. The only operations concerned

eventually after a switch are the following:

– JS(O

), JS(JS(O

)), ..., JS(O

), JS(JS(O

)), ...

– MS(O

), MS(MS(O

)), ...,MS(O

), MS(MS(O

)),

...

– MS(JS(O

)), MS(MS(JS(O

))), …,MS(JS(O

)),

MS(MS(JS(O

))), ...

– JS(MS(O

)), JS(JS(MS(O

))), ..., JS(MS(O

)),

JS(JS(MS(O

))), …

3.2.2 Swap of an operation

Let O

be a critical operation affected to a resource

and to replace on resource R

at date d. Let O

the operation executed by R

at date d. The

operations which likely to be modified are the

following:

– JS(O

), JS(JS(O

)), ...

– MS(O

), MS(MS(O

)), ...

– MS(JS(O

)), MS(MS(JS(O

))), ...

– JS(MS(O

)), JS(JS(MS(O

))), ...

– O

, JS(O

), JS(JS(O

)), ...,

– MS(JS(O

)), MS(JS(JS(O

))), ...

3.3 Initial solution

It has been shown that the efficiency of the

approaches based on local search depends closely on

the quality of the initial solution (Jain et al. 2000). In

our approach, the initial solution is determined by

the collaboration of the agent society. In the

following section, we present the Multi-Agent model

and its dynamic for determining the initial solution

and the optimal solution based on tabu search above-

mentioned.

4 MULTI-AGENT MODEL

According to Flexible Job Shop Problem definition,

we pick out two sorts of constraints: the ones

concerning the jobs, namely precedence and

temporal constraints, and those concerning the

resources, namely disjunctive constraints.

Consequently, the Multi-Agent model proposed is

composed of two agent classes: Job Agents and

Resource Agents responsible of the satisfaction of

the two classes of constraints. In addition, a third

agent class, containing a single agent, the Interface

agent, is added to our model. The latter contains the

core of the solving process, i.e. the tabu search

method. Moreover, it plays the role of the interface

between the agents and the user.

Each agent in this model has its own

acquaintances (the agents that it knows and with

which it can communicate), a local memory

composed of its static and dynamic knowledge and a

mailbox in which it stores the messages received

from the other agents. In the remaining of this

section we will describe each type of agent.

4.1 Job Agent

The acquaintances of Job agent are composed of

Resource agents that are likely to fulfil its operations

and of the Interface agent. Its static knowledge

includes its release and due dates, its process routing

and the different processing times of its operations

according to the resources. Whereas its dynamic

knowledge comprises the start times of its operations

and the current resources to which they are

allocated.

The Job agent is satisfied when all its operations

have been affected to potential resources and when

all its constraints are not violated, and in this case it

does nothing. Otherwise, it is unsatisfied and it tries

to assign an operation to an eligible resource in

cooperation with its acquaintances.

4.2 Resource Agent

The acquaintances of Resource agent are composed

of all Job agents whose operations are likely to be

fulfilled by it and of the Interface agent. Its static

knowledge encloses the list of operations that it can

perform along with their processing times. While its

dynamic knowledge is composed of the operations

currently assigned to it and their start times.

The Resource agent is satisfied when no

overlapping conflict exists between two operations

assigned to it and in this case it does nothing. If not,

it is unsatisfied and it tries to solve these conflicts by

sending one of the conflicting operation to its Job

agent in order to replace it elsewhere.

4.3 Interface Agent

The Interface agent acquaintances are composed of

all the agents existing in the system. Its static

knowledge contains:

– The maximal number of iterations allowed

Its dynamic knowledge is composed of

– The tabu list

– The current solution and its makespan

– The best solution encountered so far and its

makespan

– The current number of iterations performed.

As mentioned before, the Interface agent

contains the core of our solving process. The

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

Interface agent remains unsatisfied until the current

number of iterations exceeds a predefined threshold.

Otherwise, it delivers the best solution to the user.

In the remaining of this paper, we present the Multi-

Agent global dynamic in the two cases of initial

solution and optimal solution determination.

5 MULTI-AGENT GLOBAL

DYNAMIC

In this section we describe the global dynamic of the

Multi-Agent system proposed for the flexible job

shop problem. Two main phases compose this global

dynamic: initial solution determination phase and

optimisation phase by tabu search.

5.1 Initial solution determination

phase

The initial solution is the result of agent cooperation.

Initially, the Interface agent creates the different Job

and Resource agents and sends the message

"Determine_Initial_Allocation(J

)" to Job agents in

order to find an initial allocation for all their

operations. The job agent selects, consequently, the

less loaded resource among the potential resources

and a start time d such that:

– For the first operation of a job (according to

the process routing) d is equal to the release date of

the job.

– Otherwise, d is equal to the finish time of its

precedent operation (JP(O

)).

Such an initial allocation satisfies all precedence

and temporal constraints. However, it remains to

verify the disjunctive constraints. Each time an

operation is assigned to a resource, its Job agent

informs the concerned Resource agent through the

message "Operation_affected(R

, O

, d)". At the

receipt of this message, the Resource agent R

checks

its satisfaction. In the case that it is unsatisfied, i.e.

there is an overlapping conflict between this

operation and another operation that has been

already affected to it, it tries to find another

satisfying location on it which start time d

is the

closest possible to d. If such a location exists, then it

informs the Job agent through the message

"Operation_modified(J

, O

, d

)". Otherwise, it ejects

the operation and sends it to its Job agent in order to

search for another location through the message

"Operation_refused(J

, O

)". At this moment, the Job

agent sends the operation to another potential

resource through the message

"Place_Operation(R

, O

)".

The process above-mentioned will be repeated as

many times as the operation is not yet assigned and

for a predefined number of iterations. Once this

threshold is exceeded, namely the Job agent has not

found any location on a potential resource, it will

request one of the possible resources to create a

location through the message "Create_location(R

)". Such a location must satisfy all problem

constraints. Similarly, if the Resource agent fails in

creating such a location, it ejects the operation and

sends it to its Job agent to contact another Resource

agent, and so on. This process stops when a second

predefined threshold has been exceeded (for further

details see Ghédira & Ennigrou (2000)).

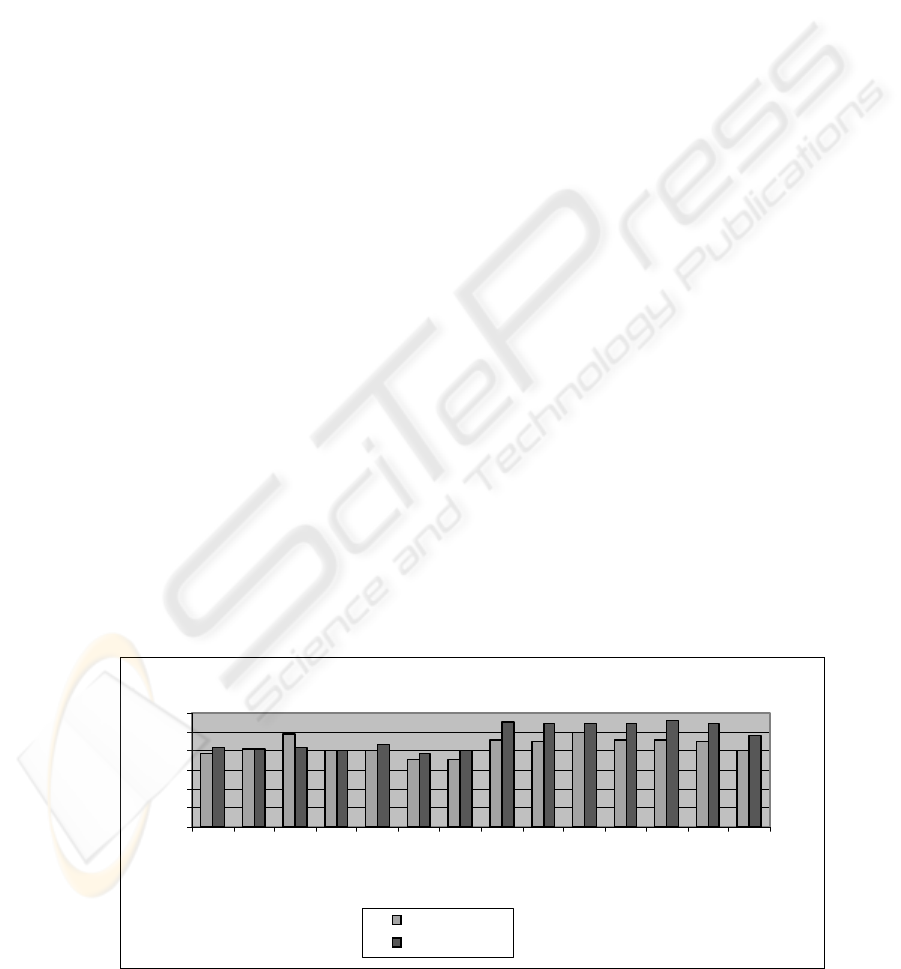
Some experiments have been made to show the

efficiency of such a system to perform good initial

solutions. The benchmarks used in this experiments

are of dimension 15x15. Figure 1 illustrates a

comparison of the performance of our approach and

the one of Mastrollili & Gambrella (2000) in terms

of Makespan.

Figure 1: Initial solution results

500

10 0 0

15 0 0

2000

2500

3000

tb4c9

tb4x

setb4xx

tb4

setb4xyz

c12

5cc

seti5x

seti5xx

seti5xyz

Notre App,

Mast&Gamb,

MULTI-AGENT APPROACH BASED ON TABU SEARCH FOR THE FLEXIBLE JOB SHOP SCHEDULING

PROBLEM

5.2 Optimisation Phase

At the end of the first phase detailed earlier, the

Interface agent receives the initial solution and

launches then the second phase, namely the

optimisation phase based on tabu search method.

The following algorithm presents the core of the

optimisation process implanted in the Interface

agent.

1. tabu_list

←

∅

2. nb_iter

←

3. current_sol

←

initial_solution

4. best_sol

←

current_sol

5. while nb_iter <= nb_iter_max do

6. iter

←

7. while iter <= iter_max & nb_iter <=

nb_iter_max do

8. path

←

critical_path (current_sol)

9. neighbourhood

←

determine_

neighbourhood (path)

10. best_neighbour

←

determine_best_

neighbour(neighbourhood

11. tabu_list

←

add_in_tabu_list(best_neighbou

12. current_sol

←

perform_mvt

(current_sol,best_neighbour)

13. if cost(current_sol) < cost(best_sol) then

14. best_sol

←

current_sol

15. nb_iter

←

End if

16. nb_iter

←

nb_iter+1

17. iter

←

iter+1

End while

18. Diversification

End while

Once the best neighbour among the

neighbourhood of the current solution has been

chosen, the Interface agent sends the operation

concerned to its Job agent through the message

"Place_Operation (J

, O

, R

)" in order to inform it

about the move to perform. At the receipt of this

message, the Job agent sends this operation to the

Resource agent R

in order to find a location starting

at date d satisfying all problem constraints through

the message "Operation_allocated(R

, O

, d)". The

same process described in the first phase will be then

repeated.

When the number of iterations between two best

solutions exceeds a predefined threshold "iter_max",

a diversification phase is performed. The latter

consists in varying the search in order to explore

new regions of the search space. In our approach,

such a phase is characterized by replacing some

operations selected randomly. An operation is

replaced on one of its potential resources selected

also randomly.

6 ILLUSTRATIVE EXAMPLE

Let we consider a flexible Job Shop problem of

dimension 3x3. The following table describes the

processing times of the different operations on the

different resources.

x 8 x

x 6 x

11 2 x

x 3 10

11 x 10

12 x 12

4 x 12

12 x x

Table1: Processing times of a flexible Job Shop problem

3x3

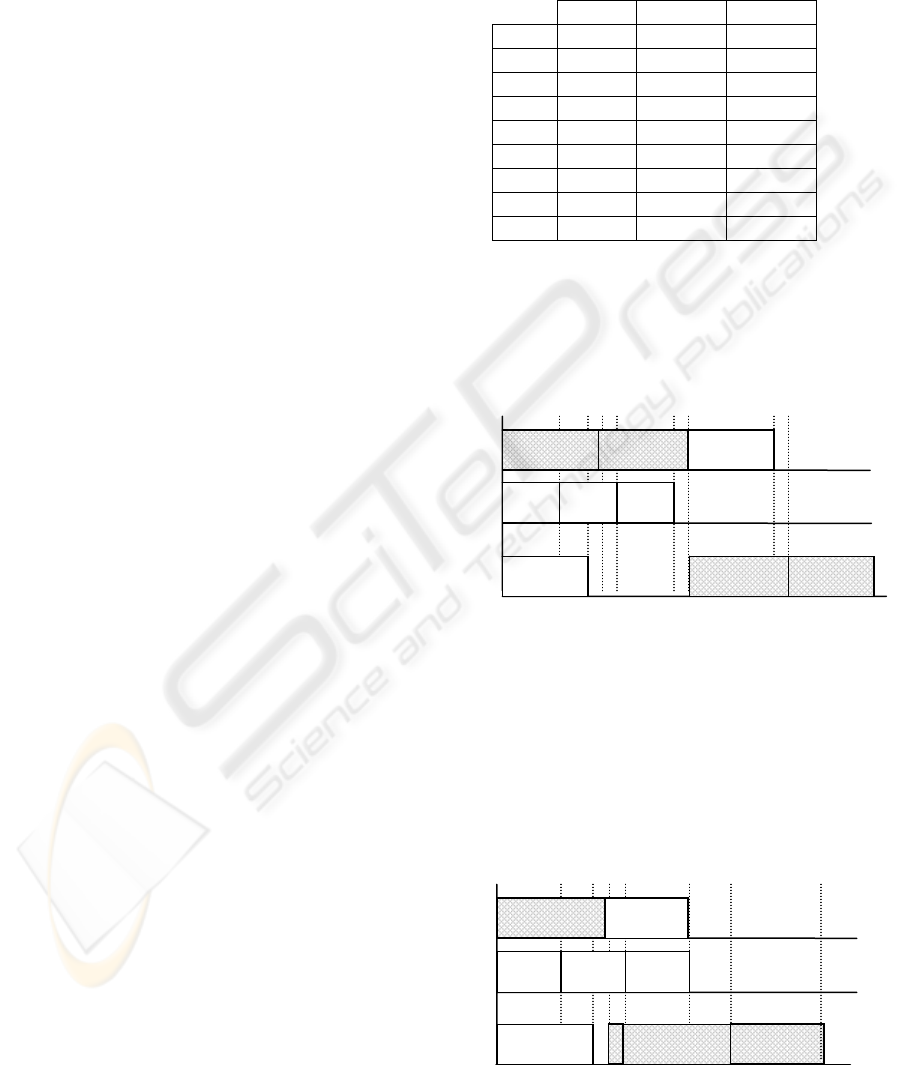
Figure 2 shows the initial solution provided by

the first phase of our approach. The critical path is

composed of the operations O

, O

. The

cost of this solution is equal to 47.

Figure 2: Initial Solution

The neighbourhood of the current solution is

composed of the following possible moves:

– Replacement of O

on M

– Replacement of O

on M

– Swap of O

and O

– Replacement of O

on M

The best neighbour among the previous moves is

the replacement of O

on M

, which cost is 39.

Figure 3 illustrates the new solution obtained.

Figure 3: Iteration 1 of the tabu search.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

Figure 4: Iteration 2 of the tabu

Figure 5 shows the final solution obtained by the

solving process.

Figure 5: Optimal solution

7 EXPERIMENTS

Some experiments have been made on various

benchmarks defined by Brandimarte (1993),

Dauzerre-Peres & Paulli (1997), Chambers and

Barnes (1996) and Hurink et al. (1994). These

benchmarks have a number of jobs varying in the

set{10, 15, 20}, the number of resources in the range

[5, 20], the number of operations per job in the range

[5, 25] and the number of potential resources per

operation in the range [1, 3]. Consequently, the

benchmarks considered have a total number of

operations ranging in [50, 500].

For each benchmark, many executions have been

performed due to the great number of parameters to

define in the tabu search method and also due to the

random character of the diversification process. Five

executions have been performed for each instance

and for each parameter. The results mentioned later

show the minimum of the five iterations.

The parameters used in the tabu search are the

following:

– Tabu list size varying in {7,10,15,20,30}

– Total number of iterations nb_iter_max fixed

to 1000

– Number of iterations between two

diversification phases iter_max varying in

{250,300,350}

Figure 6 points up a comparison between the

initial solution and the optimal solution elaborated

by the two phases of our approach as same as the

lower and the upper bounds presented in the

literature for the same instances. This figure shows

that our approach provides optimal solutions

belonging to the range defined by the lower and the

upper bound.

Figure 6: Brandimarte Benchmarks

200

400

600

800

1000

1200

Mk01

Mk0

Mk1

Min

MULTI-AGENT APPROACH BASED ON TABU SEARCH FOR THE FLEXIBLE JOB SHOP SCHEDULING

PROBLEM

8 CONCLUSION

In this article we have presented a Multi-Agent

approach for solving the flexible Job Shop problem.

This approach is based on the tabu search method.

The Multi-Agent system proposed is composed of

three agent classes: Job agents, Resource agents and

an Interface agent. Each agent class is responsible

for the satisfaction of the constraints under its

jurisdiction. Some experiments have been made on a

plenty of benchmarks. The results provided show a

substantial difference in cost between the initial

solution and the optimal one as same as the

existence of the latter solution in the range defined

by the lower and the upper bounds given in the

literature. Our perspectives are to distribute the tabu

search process between the society of agents in order

to make the decision shared between the agents

instead of its centralisation in the Interface agent.

REFERENCES

Brandimarte P. (1993). Routing and scheduling in a

flexible job shop by tabu search. Annals of Operations

Research 22. pp 158-183.

Brucker, P. et Neyer, J. (1998). Tabu-search for the multi-

mode job-shop problem. OR Spektrum 20, 21-28.

Chambers et Barnes (1996). Flexible Job Shop scheduling

by tabu search. Graduate program in Operations

Research and Industrial Engineering, The university

of Texas at Austin, Technical Report series, ORP96-

09.

Dauzerre-Peres S., Paulli J. (1997). An integrated

approach for modeling and solving the general multi-

processor job shop scheduling problem using tabu

search. Annals of Operations Research 70, 281-306.

Eikelder T., H.M.M., Aarts, B. J. M., Verhoeven, M. G. A.

and Aarts, E.H.L. (1997). Sequential and Parallel

Local Search Algorithms for Job Shop Scheduling.

MIC'97 Proceedings of the 2nd International

Conference on Meta-heuristics, Sophia-Antipolis,

France, pp. 75-80.

Ghédira K. et Ennigrou M. (2000). How to schedule o Job

Shop Problem through agent cooperation. AIMSA

2000: Aritificial Intelligence: Methodology, Systems,

Architectures.

Glover F. (1986). Future paths for Integer Programming

and Links to Artificial Intelligence,.Computers and

Operations Research, 5:533-549.

Hurink E., Jurisch B., Thole M. (1994). Tabu search for

the Job Shop scheduling problem with multi-purpose

machine. Operations Research Spektrum 15, 205-215.

Jain A., Rangaswamy B., Meeran S. (2000). Job shop

neighbourhoods and Move evaluation strategies.

Mastrolilli M., Gambardella L.M. (2000). Effective

Neighborhood Functions for the Flexible Job Shop

Problem. Journal of Scheduling, Volume 3, Issue 1.

Pages:3-20.

Nuijten W., Aarts E. (1996). A computational study of

Constraint Satisfaction for multiple capacitated Job Shop

scheduling. European Journal of Operations Research,

90(2): 269-284.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS