
MONTHLY FLOW ESTIMATION USING ELMAN NEURAL
NETWORKS
Luiz Biondi Neto, Pedro Henrique Gouvêa Coelho, Maria Luiza Fernandes Velloso
Electronics and Telecommunications Department, State University of Rio de Janeiro,
R
ua São Francisco Xavier, 524, Bl.
A,
Sala 5036, Maracanã, 20550-013, Rio de Janeiro, RJ, Brazil
João Carlos C. B. Soares de Mello
Production Engineering Department, Fluminense Federal University, Rua Passo da Pátria, 156, São Domingos, 24240-
240, Niterói, RJ, Brazil
Lidia Angulo Meza
Technology Science Institute
Veiga de Almeida University, Rua Ibituruna 108, Maracanã, 20271-020, Rio de Janeiro, RJ, Brazil
Keywords: Time series estimation, Flow Estimation, Elman Neural Networks
Abstract: This paper investigates the application of partially recurrent artificial neural networks (ANN) in the flow
estimation for São Francisco River that feeds the hydroelectric power plant of Sobradinho. An Elman neural
network was used suitably arranged to receive samples of the flow time series data available for São
Francisco River shifted by one month. For that, the neural network input had a delay loop that included
several sets of inputs separated in periods of five years monthly shifted. The considered neural network had
three hidden layers. There is a feedback between the output and the input of the first hidden layer that
enables the neural network to present temporal capabilities useful in tracking time variations. The data used
in the application concern to the measured São Francisco river flow time series from 1931 to 1996, in a total
of 65 years from what 60 were used for training and 5 for testing. The obtained results indicate that the
Elman neural network is suitable to estimate the river flow for 5 year periods monthly. The average
estimation error was less than 0.2 %
.
1 INTRODUCTION
The Brazilian hydroelectric system presents peculiar
aspects that make it different from other such
systems. First, Brazilian rivers flow characteristics
show a strong seasonality and a high degree of
uncertainty on the opposite of north hemisphere
systems in which the hydrologic regimen is ruled
basically by ice melting. Second, the Brazilian
system shows an isolating system characteristic
lacking interconnection with neighbouring
thermoelectric systems as opposite to typical
hydroelectric systems. And finally it shows a strong
hydraulic coupling among its unities.
Thus, the operation planning of such plants
depends on a previous knowledge of water volume
available in the corresponding reservoirs, i.e. it is
necessary to know the volume of water that will be
available in advance in order to estimate the
maximum level of energy to be generated by the
plant. So it is possible to carry out the energy
planning having good flow estimates in order to
optimize the energy processing generation.
To that end, there are measuring units along
specific sites on the rivers comprising the
hydrographical basin that produce discrete flow
measures making possible the composition of
history flow series. The estimation of flows
153
Biondi Neto L., Henrique Gouvêa Coelho P., Luiza Fernandes Velloso M., Carlos C. B. Soares de Mello J. and Angulo Meza L. (2004).
MONTHLY FLOW ESTIMATION USING ELMAN NEURAL NETWORKS.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 153-158
DOI: 10.5220/0002610101530158
Copyright
c
SciTePress

comprises the determination, in advance, of the
values of water volume that will reach the measuring
units based on the available history series
(Chatfield,1991).
The flow estimate is a true challenge used for
the management of hydrological resources of a
certain river basin (Moraes, 1995,1996). The
predictions of flood, sole humidity for agriculture,
levels of river navigation, the available water
capability for water distribution, irrigation and
energy production are possible with river flow
estimation (Tucci, 2002). The flow estimation can be
performed for short, medium or long term. (Tucci,
2002). The short term prediction is used to estimate
the flow in a basin location within some hours or
days in advance. The medium term prediction
involves the flow prediction within one to several
months in advance and depends strongly on weather
and ocean conditions that might influence the values
of future flows. Finally, the long term prediction
deals with the estimation of the risks of certain
levels of flows, usually done statistically, in a certain
site in the river basin. For instance, the flood risk in
a certain river section, the chances of dry and wet
periods, etc (Tucci, 2002).
Traditionally the electric sector uses the Box-
Jenkins method (Box, 1976), (Hoff, 1983) for
predicting the river flow that supposes a linear
relationship among the present and past flow values.
Linear models usually considered are autoregressive
(AR), moving average (MA) and the autoregressive
moving average (ARMA) that might no be suitable
to deal a data set having non linear and non
stationary characteristics such as the flow series
(Chatfield, 1991).
On the other hand, artificial neural networks
(ANN) (Fog, 1995), (Lach
termacher, 1995), (Sarle,
1995) are models comprising a number of non linear
elements, the neurons, working in parallel and
organized in layers such as their biological
counterparts. They can learn certain knowledge by
experience (Haykin, 1994), (Evans, 1991), (Siqueira,
2002). The ANNs can be of two types: feedforward
and recurrent networks. The neural networks with no
feedback are static i. e. a certain input only produces
a set of outputs with no memory capability.
Recurrent neural networks are able to memorize
temporal information. A typical case is the Elman
network (Elman, 1990), which is partial recurrent
and will be used in this paper for estimating the river
flow.
The main advantages in using the ANN
approach compared to the classical methods are:
• ANNs are faster than most current
statistical techniques;
• ANNs are self-monitoring, i.e. they learn
how to perform accurate predictions;
• ANNs are able to carry out iterative
predictions;
• ANNs are able to deal with non stationarity
and non linearity of the investigated time
series;
• ANNs offer both parametric and non
parametric prediction;
Several researchers have done work in this area.
Zurada in 1997 (Zurada, 1997) introduced the
concept of sequential neural networks using an
Elman network. Aquino (Aquino, 1999) uses ANNs
in the planning for hydrothermal generated systems
operation. Millioni (Millioni, 2000) tries to
circumvent the physical nature process using a
system that makes use, in a first step, of econometric
models dealing with multiple regressions to explain
the flow of a river section from the observation of
the backward river level. Tucci (Tucci, 2001) shows
the real time prediction result for the river volume at
Ernestina reservoir.
This work has the objective to investigate the
estimation of the river flow in a 5 year period
monthly in order to aid the electrical sector involved
in energetic planning.
The importance of the flow prediction can be
better appreciated by the fact of the existence of an
energy surplus not used, coming from the difference
between the average generation in all flow history
(medium and long term) and the firm energy.
The paper is organized in 5 sections. The first
introduces the subject reviewing other works done
earlier.
Section 2 shows theoretical foundations on
Elman neural networks. Section 3 describes the
problem modelling. Section 4 show numerical
results and section 5 concludes the paper.
2 BASIC FOUNDATIONS
Static neural networks such as multiple layer
perceptrons (MLP) trained with the backpropagation
algorithm (Cichocki, 1996), are not suitable for
dynamic mappings (Haykin, 1994).
As a consequence learning the temporal
characteristics of a signal containing the history river
flow can be a difficult task.
In order to solve the problem, a traditional MLP
could be used with inputs delayed in time. Figure 1
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
154

shows that arrangement called temporal network in
which a MLP network is fed by an input u(t) that is
successively delayed in time until u(t-k) and has as
output y(t) = u(t). In that case, the delay operator is
being applied only at the input but it could be
applied either in the hidden layers or at the output.
Another way to solve the problem is to use
networks with feedback called recurrent neural
networks. Usually recurrent neural networks can
incorporate a MLP or part of it. In general such
networks are suitable for dealing problems with
temporal characteristics.
Recurrent neural networks can have one or more
feedback loops. Those fully recurrent every neuron
is connected to all others and constitute the more
general case of ANNs.
Figure 1: Temporal network
An elegant way to represent a neural network is
using a state space model. The notion of state plays
an important role in the mathematical formulation of
a dynamical system. The state of a system is
formally defined as the set of quantities that
synthesises all the information about the past
behaviour of the system that is needed to uniquely
describe its future behaviour, except for the purely
external effects arising from the applied input or
excitation. Let the [q x 1] vector x(k) be the state of
a discrete non linear system. Let the [m x 1] vector
u(k) be the applied input to the system and the [p x
1] vector y(k) its output. In mathematical terms, the
dynamic behaviour of the system, assumed to be
noise free, is described by the following pair of non
linear equations.
))()(()1( kWkWk
ba
uxx +=+
ϕ
(1)
)()( xCk
x
y
= (2)
where W
a
is a [q x q] matrix, W
b
is a [q x m] matrix,
C is a [p x q] matrix , and
qq
ℜ→ℜ:
ϕ
is a map
described by:
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
→
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
)(
.
.
.
)(
)(
.
.
.
:
2
1
2
1
qq
x
x
x
x
x
x
ϕ
ϕ
ϕ
ϕ
(3)
for some memoryless component-wise nonlinearity
ϕ: ℜ→ℜ. The spaces ℜ
m
, ℜ
q
, and ℜ
p
are named the
input space, state space and output space
respectively. It can be said that q, that represents the
dimensionality of the state space is the order of the
system.
The recurrent neural network represented by
equations (1) and (2) is a dynamic system with m
inputs and p outputs of order q. Equation (1) is the
process equation and equation (2) the measurement
equation. Regarding matrices W
a
, W
b
and C, and
the non linear function ϕ(.) the following can be
said.
W
a
contains the synaptic weights of the q
processing neurons which are connected to the
feedback nodes in the input layer. W
b
contains the
synaptic weights for each one of the q neurons that
are connected to the input neurons, and C defines
the combination of neurons that will characterize the
neural network output. The nonlinear function ϕ(.)
characterizes the activation function of any neuron
in the neural network. This function is usually
defined by the hyperbolic tangent (4).
x
x
e
e
xx
2
2
1
1
)tanh()(
−
−
+
−
==
ϕ
(4)
An important property of a recurrent neural
network described by state space equations (1) and
(2) is its capability to approximate a wide class of
non linear dynamic systems.
Figure 2 shows a recurrent neural network with
three inputs, three states and one output, i.e. m=3,
q=3 and p=1.
MONTHLY FLOW ESTIMATION USING ELMAN NEURAL NETWORKS
155
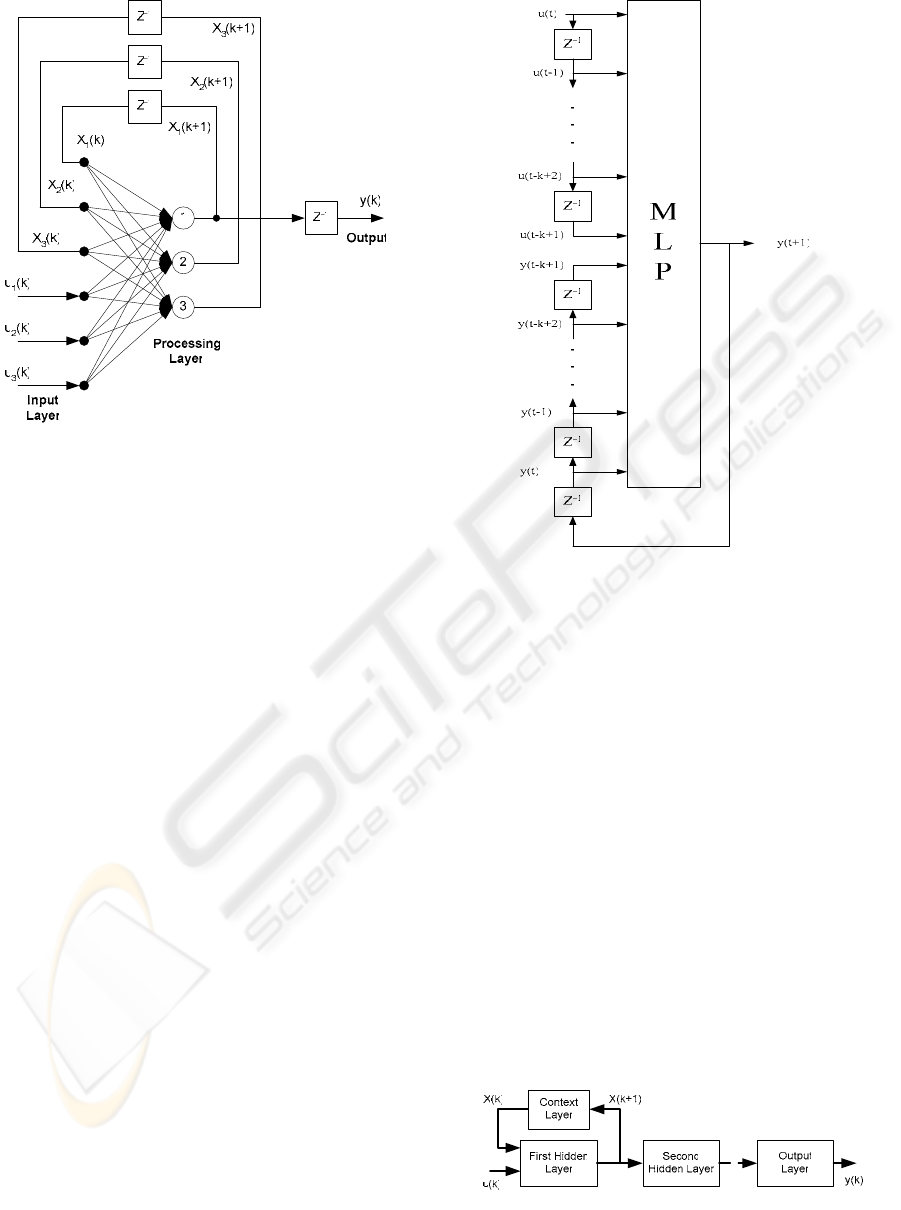
Figure 2: Fully Recurrent Neural Network
Matrices W
a
e W
b
are defined by:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
333231
232221
131211
www
www
www
W
a
(5)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
363534
262524
161514
www
www
www
W
b
(6)
Matrix C a line vector defined as:
]001[=C (7)
Figure 3 represents a nonlinear autoregressive
model with exogenous inputs (Haykin, 1994). The
model has a delay line memory with k unities in the
input. A unit delay output is also feedback to the
input. The output will be one time unit advanced
relatively to the input.
The current and past input values are denoted by:
u(t), u(t-1) u(t-2) ... u(t-k+1) and the corresponding
output values: y(t), y(t-1) y(t-2) ... y(t-k+1) over
what a regression is performed modeled by the non
linear map
ℑ as shown in equation (8).
y(t+1)=
ℑ(y(t), …,y(t-k+1), u(t), …u(t-k+1)) (8)
Figure 3: Recurrent Network Structure
The Elman network was used in this paper which
is considered as a partially connected ANN as the
feedback loops are placed between the output and
the input of the first hidden layer.
The recurrent loop is performed by what is called
a context unit, usually a delay structure storing the
outputs of the first hidden layer. So, that sort of
structure enables a time varying pattern generation,
which makes it suitable for applications involving
time series data. Besides the recurrent layer, the
neural network can have several other layers
comprising a traditional MLP having one or several
outputs.
The chosen training algorithm was the
backpropagation widely discussed in the literature
(Haykin, 1994) and (
Cichocki, 1996).
Figure 4 depicts an Elman network showing
clearly the working mechanism of the feedback
structure.
Figure 4: Elman Network
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
156
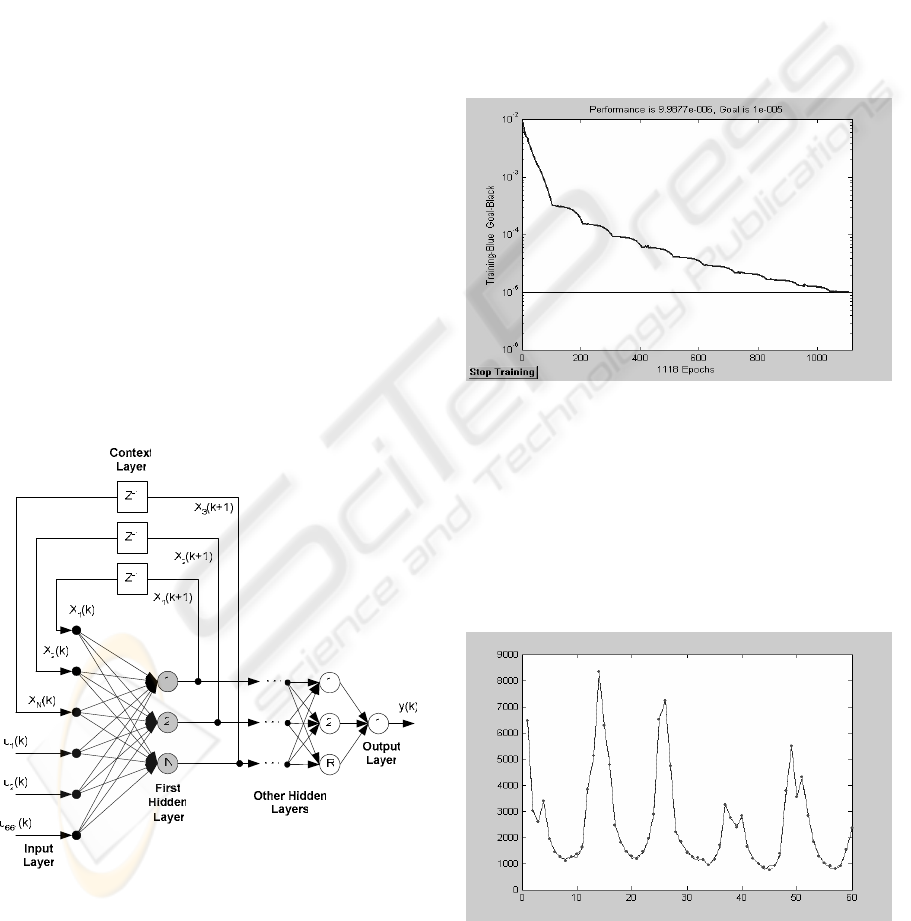
3 MODELLING
In this paper, a model similar to the one shown in
figure 4, is used for 60 month periods delayed one
another by one month.
The available database covers 65 years of the
São Francisco river flow, month by month. From
those data, 60 year data is used for the network
training, leaving for test the remaining 5 year data.
The training data are arranged in an input matrix
containing 661 rows, delayed by one month and 60
columns concerning to a 5 year period. The target
vector has 60 elements delayed by one month
relative to the last row of the input matrix.
Figure 5 shows the network model used in the
tests.
The optimum number of neurons in the hidden
layers is chosen heuristically according to training
results for optimizing the neural network
performance particularly regarding generalization.
The output layer has only one neuron that will
produce a vector with 60 elements representing the
predicted river flow values for five years monthly.
The backpropagation algorithm was used for
training the neural network in in order to adjust its
feedforward weights. The recurrent weights are
fixed to one as usually done in Elman neural
networks.
Figure 5: Used Neural Network Model
4 RESULTS
Several Elman ANNs were tested in order to obtain
the best generalization characteristics. The best
architecture resulted in an Elman neural networks
with three hidden layers (357-186-51) and one
output layer with one neuron which uses the
hyperbolic tangent as its activation function. The
used criterion for error minimization was the
gradient descent with adaptive learning rate and a
momentum coefficient to minimize the fluctuations
in the learning curve. Convergence was achieved
after 1118 epochs for an error goal of 10
-5
and the
resulting learning curve is shown in figure 6.
Figure 6: Learning Curve
The weights achieved by training the Elman
ANN are stored in a file for later use for the monthly
river flow prediction for a five year period. Figure 7
shows the original test data comprising the last five
year flow data reserved for test, (continuous curve)
and the prediction curve (dotted line curve) obtained
by the Elman ANN. The resulting prediction average
error was less than 0.2 % .
Figure 7: Prediction Curve
m
3
/s
month
MONTHLY FLOW ESTIMATION USING ELMAN NEURAL NETWORKS
157
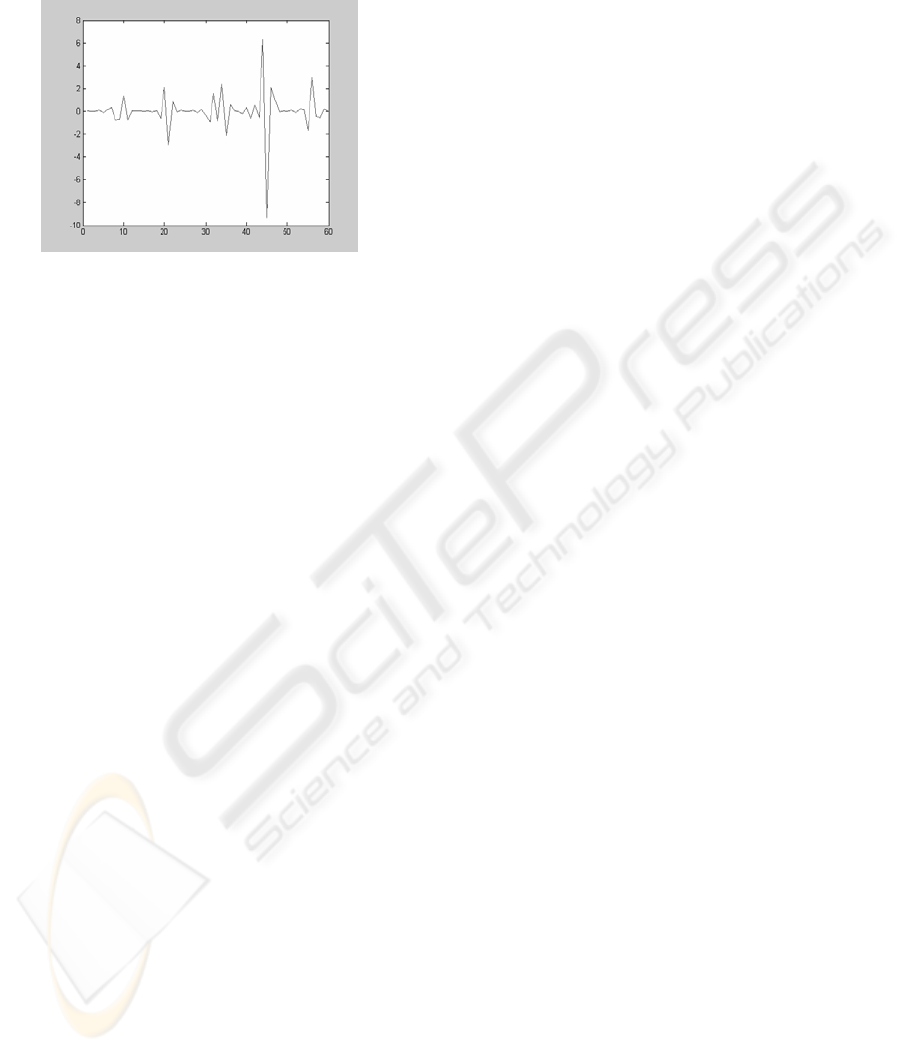
Figure 8 shows the prediction error curve where
it can be seen that the average error is not greater
than 0.2 %.
Figure 8: Percentage Error Curve
5 CONCLUSIONS
The results achieved by the use of the proposed
Elman ANNs for river flow prediction indicate that
they are quite adequate for the flow estimation task.
In the investigated application, the average
prediction error of about 0.2% is much less than that
obtained by traditional ANNs using data Windows
(Haykin, 1999) typically in the order of 5%.
Statistical methods used for flow prediction such as
Box & Jenkins and its variations (Box and Jenkins,
1976) yield an average error larger than 10 %.
For future work, suggestions include the use of
fully recurrent ANNs and ocean temperature data
added to the neural network input. Ocean
temperature is known to have a significant influence
on the river flow values so that sort of information
will be certainly useful for the neural network in
consideration.
REFERENCES
Chatfield E., 1991. The Analysis of Time Series, New
York, USA, Chapman and Hall, fourth edition.
Moraes, J. M., Pellegrino, G., Ballester, M. V., Martinelli,
L. A., Victoria, R. L., 1995. Hydrological Parameters
of a Southern Brazilian Watershed and its Relation to
Human Induced Changes. In Annales of 20th General
Assembly of the European Geophyscial Society, v13:
506-507.
Moraes, J. M., Genovez, A.M., Mortatti, J.,
Pellegrino,G.,Ballester, M.V., Martinelli, L. A, 1996.
Analyses and Modelling of a Flow Time Series under
the Influence of Man Made and Natural Actions. In
Anais do XVII Congresso Latino Americano de
Hidraúlica. (in Portuguese)
Tucci, C. E. M., Robin T. C., Dias P. L. da S., Collischonn
W., 2002. Medium Run Prediction of Reservoirs Flows
based on Weather Forecast. In Final Project
Report:BRA/00/029, Instituto de Astronomia, Geofísica
e Ciências Atmosféricas Universidade de São Paulo
and Instituto de Pesquisas Hidráulicas Universidade
Federal do Rio Grande do Sul. (in Portuguese)
Box, G. E. P., and Jenkins, G. M., 1976. Time Series
Analysis: Forecasting and Control. California, USA.
San Francisco: Holden Day, 2nd. ed.
Hoff C. J., 1983. A Practical Guide to Box-Jenkins
Forecasting, Belmont, CA., USA, Lifetime Learning
Publications.
Fog, T.L. et al, 1995. Training and Evaluation of Neural
Networks for Multi-Variate Time Series Processing. In
Proceedings of IEEE International Conference on
Neural Networks. IEEE Press.
Lachtermacher, G. and Fuller, J.D., 1995.
Backpropagation in Time series Forecasting. In
Journal of Forecasting. Vol 14, 381-393.
Sarle, W.S., 1995. Stopped Training and other remedies
for Overfitting. In Proceedings of the 27th Symposium
on the Interface.
Haykin, S. Neural Networks : A Comprehensive
Foundation, Prentice-Hall, New Jersey, 1999.
Evans, R. M. and S. Alvin, J., 1991. Relating Numbers of
Processing Elements in a Sparse Distributed Memory
Model to Learning Rate and Generalization, In ACM
APL Quote Quad, v21(4), 166-173.
Siqueira, T. G., Soares Filho, Secundino, 2002.
Application of Neural Networks with Radial Basis
Activation Function to the prediction of Non-
stationary Time Series, In XIV Congresso Brasileiro de
Automação. (in Portuguese)
Elman J. L., Finding Structure in Time, 1990. In
Cognitive Science, vol. 14, pp. 179-211.
Jacek M. Zurada and Tomasz J. Cholewo, 1997.
Sequential Network Construction for Time Series
Prediction. In Proceedings of the IEEE International
Joint Conference on Neural Networks, pp 2034–2039.
Ronaldo R. B. de Aquino, Manoel Afonso de Carvalho Jr.,
Benemar Alencar de Souza, 1999. Artificial Neural
Networks: An Application to the Operation Planning of
Hydrothermal Generation Systems. In Proceedings of
the IV Brazilian Conference on Neural Networks - IV
Congresso Brasileiro de Redes Neurais, pp. 164-169.
(in portuguese)
Armando Zeferino Milioni e Acioli Antonio de Olivo,
2001. Econometric Models for the Forecast of River
Floods . In Simpósio Brasileiro de Pesquisa
Operacional. (in portuguese)
Tucci, C. E. M., Brun, Gerti, 2001. Real Time Forecast of
the Volume Flowing to the Reservoir of Ernestina. In
Revista Brasileira de Recursos Hídricos. v.6, n.2, p.73
– 79. (in Portuguese)
Cichocki, A., Unbehauen, R., 1996. Neural Networks for
Optimisation and Signal Processing, New York, USA,
John Wiley & Sons, Inc.
month
error %
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
158
