FACE PATTERN DETECTION

An approach using neural networks

Adriano Martins Moutinho, Antonio Carlos Gay Thomé

Núcleo de Computação Eletrônica, Universidade Federal do Rio de Janeiro, Rio de Janeiro,Brasil

Luiz Biondi Neto, Pedro Henrique Gouvêa Coelho

Faculdade de Engenharia, Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brasil.

Keywords: Face detection, neural networks, image processing.

Abstract: Security systems based on face recognition often have to deal with the problem of finding and segmenting

the region of the face, containing nose, mouth and eyes, from the rest of the objects in the image. Finding

the right position of a face is a part of any automatic identity recognition system, and it is, by itself, a very

complex problem to solve, normally being handled separately. This paper describes an approach, using arti-

ficial neural networks (ANN), to find the correct position and separate the face from the background. In

order to accomplish this goal, a windowing method was created and combined with several image pre-

processing steps, from histogram equalization to illumination correction, as an attempt to improve neural

network recognition capability. This paper also proposes methods to segment facial features such as mouth,

nose and eyes. Finally, the system is tested using 400 images and the performance of face and facial features

segmentation is presented.

1 INTRODUCTION

The human face, in this paper, is defined as the

smallest rectangle that contains the mouth, nose and

eyes of the person, in such way that it is possible to

separate these elements from the other objects in the

image.

Figure 1 illustrates an example of face segmen-

tation as it is defined here. This is a very difficult

task and in order to succeed, any face detection

system must be able to handle several problems like

presence of beard, mustache, skin color variations,

head inclination and face rotation.

Figure 1: Face example

One of the objectives in this research is to make

the system, as much as possible, immune to these

variations.

The human frontal face, as defined in figure 1,

.is a very distinguished pattern, making the MLP

neural network (Haykin, 1999) a nice choice to

achieve good results. A neural network could be

trained using several sequences of face images, as

shown in figure 2, and many other non-face images

containing geometric shapes, noise and variations

(Rowley, 1999).

Figure 2 shows examples of face and non-face

databases (Rowley, 1999):

Figure 2: Face (left) and non-face (right) database (Row-

ley, 1999)

172

Martins Moutinho A., Carlos Gay Thomé A., Biondi Neto L. and Henrique Gouvêa Coelho P. (2004).

FACE PATTERN DETECTION - An approach using neural networks.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 172-177

DOI: 10.5220/0002610301720177

 SciTePress

Figure 3: System general view

2 FACE DETECTION SYSTEM, A

GENERAL VIEW

The proposed face segmentation can be divided into

four main modules, as shown in figure 3.

The first module, called windowing, splits the

main picture into squared 19x19 sized sub-images

using an edge seek method, as described in section

3; the second module, called image preprocessing

and coding, described in section 4, prepares the

image signal to improve ANN generalization. Sev-

eral processing steps such as contrast stretch and

illumination correction are applied; the third module

corresponds to an MLP neural network, trained

using databases such as the ones in figure 2. All the

sub-images identified as faces by the ANN are

passed to the fourth module, where face framing is

optimized using a recursive process, in order to

obtain the smallest rectangle that contains the face,

according to the definition presented in section 1.

These adjustments are further described in section 5.

3 WINDOWING

As long as any part of the image, independently of

size or proportion, could contain the desired face,

the windowing module must extract from the origi-

nal image, every possible and distinct rectangular

sub-images, sending them all to the pre-processing

module and then to the neural network, trained to

recognize face patterns. Although this method is

theoretically possible, it would require too much

processing time, because even from a small image

would be possible to extract various distinct sub-

images.

The method suggested in this paper seeks for

faces only around image edges, extracting only sub-

images that contain at least one edge pixel. Figure 4

shows an example of this process. It can be clearly

observed that a face will always contain edge pixels.

Figure 4: Edge windowing example

Even so, the number of distinct images could be

very high. A solution to that would be to first con-

sider the sub-images as a square, not as a rectangle,

and only in a fine adjustment, as described in section

5, it will be optimized to better encompass the face.

After windowing, every extracted image is re-

sized to 19x19 and passed to the preprocessing

module, described in section 4. The windowing

method first computes edge points in the image and

assembles them in a sorted list (according to its

distance to the origin). Then, an adjustable square,

initially 19x19 sized, is centered on the first point in

the list and extracts a sub-image.

4 IMAGE PRE-PROCESSING AND

CODING

In order to obtain a good generalization, it is neces-

sary to do some processing before applying the

signal to the ANN. In the specific case of face pat-

tern detection, it is important to apply a process that

emphasizes the differences between faces and non-

faces images (Rowley, 1999).

Thus, a sequence of transforms is applied, in-

cluding histogram equalization (Gonzalez, 1992),

oval filtering, and illumination correction, as shown

in figure 5.

FACE PATTERN DETECTION - An approach using neural networks

173

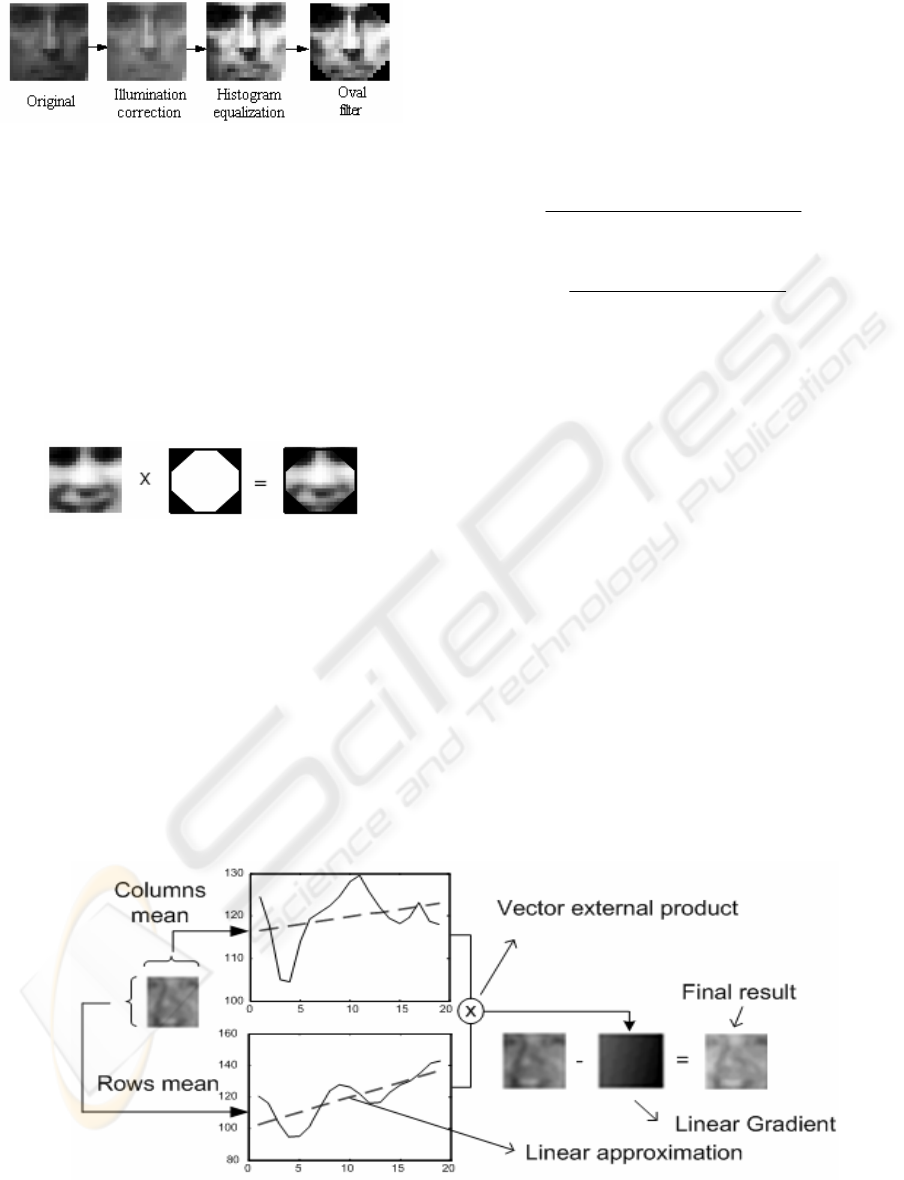
Figure 5: Preprocessing steps, order of application

The histogram equalization is applied following

the traditional methods (Gonzalez, 1992), its objec-

tive is to raise image contrast.

The oval filter follows the principle that pixels

in the borders of face images do not contain relevant

information and could be masked, this operation

does not change a face to a non-face, or vice-versa

(Rowley, 1999). This mask allows the network,

during the training process, to avoid consider such

points, which tend to favor generalization.

Pixel elimination is done by adjusting triangular

masks to the sides of a face, as shown in figure 6.

Figure 6: An oval filter example

Illumination correction is the key point to a reli-

able recognition. It is designed to remove the effect

of regular illumination.

If light effect is presumed to be a linear func-

tion, an image where some illumination is applied

could be decomposed into a linear gradient and a

non-illuminated image. To find this gradient directly

from an already illuminated image, a method is

proposed where the mean of grayscale values of

both columns and rows of an image is calculated.

So, a vector of all row means and a vector of

columns means are build. Linear approximations of

these vectors are computed using the minimum

square method, shown in equations 1, 2 and 3. The

Linear equation is

=+, where z is the mean

of grayscale values, w is the column or row number

and a and b are the linear coefficients of the ap-

proximation. Figure 7 shows a practical example of

this process.

bawz +≅

(1)

()

www

zw w

⋅−⋅⋅

⋅−

∑

∑∑∑

∑∑

(2)

(

)

wz w

zw w

⋅⋅−⋅

⋅−

∑

∑∑

(3)

The next step is to build a matrix with character-

istics extracted from the image. This process is

called coding, where the lines of the pre-processed

image are concatenated creating a matrix containing

all face examples. The next step is subject the matrix

to a statistic method called principal components

analysis (PCA) (Haykin, 1999), (Johnson, 1998).

The PCA method applies a linear transformation

to the subspace and removes those dimensions with

low variance. It can reduce the size of a training

vector without losing much information. PCA appli-

cation (Haykin, 1999) (Johnson, 1998) results in a

size reduced vector and a transformation matrix,

used to map new data into the same reduced form. In

this paper, the computation of the transform matrix

is done using only the face database, as shown in

figure 2.

The best neural network configuration has one

hidden layer with around 150 neurons. The activa-

tion function is hyperbolic-tangent for the hidden

layer and sigmoid for the output layer.

Figure 7: Illumination correction method

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

174

Figure 8: Centroid and Successive comparison reduction

5 FINE ADJUSTMENT

The recognition method proposed here tends to iden-

tify the same face several times, on adjacent squares,

as shown in figure 8.

However, this cannot be considered as a disad-

vantage, since all these multiple detections can be

used to validate and find the correct face position

through a process called Centroid Reduction.

Let rectangles A and B be called “Centroid

neighbors” if the centroid of A is within rectangle B

and vice-versa. This definition can be extended to n

rectangles. Figure 8 shows many centroid neighbors,

shown in yellow color.

The centroid reduction method replaces all

“centroid neighbors” by the average square. Squares

that do not have any neighbors are ignored because

they are more likely to be a mistake made by the

ANN. Figure 8 shows an example of centroid reduc-

tion. All yellow squares are replaced by another one

that is computed using the average. The red square

in figure 8 is ignored during the process because it

does not have any “centroid neighbors”.

After centroid reduction, another fine adjust-

ment is made. It is called successive comparison

reduction. From the face position that is the output

of centroid reduction, other faces are generated by

shifting the original rectangle shape one pixel to the

left, right, bottom and top. Other faces are also cre-

ated from the original one, having one pixel width

and height less. All of these faces along with the

original image are again submitted to the neural

network, in a greedy search recursive process, where

the actual face is the higher output value of the neu-

ral network. This process repeats itself until there is

no change in rectangle position between two phases.

Figure 8 also shows the successive comparison ad-

justment method. The result rectangle is smaller and

more adapted to the face than the input square.

6 FACE ELEMENTS

LOCALIZATION

Once the face is located, simple techniques can be

developed to find each face element of the subject.

This is possible because if the smallest rectangle that

contains the face is known, it can be said that all

face elements respect a specific geometry that helps

the task of finding every sub-part of face, such as

eyes, mouth and nose.

6.1 Eye pattern localization

With the smallest rectangle that covers the face, it is

possible to guarantee that the eyes are on the supe-

rior half of this rectangle. It is also possible to admit

that if this superior part is again divided in two

halves, one will be very likely to contain the left eye

and the other the right one.

So, to obtain the right position of both eyes, 2d

cross correlation between the right and left halves

and an eye standard pattern are computed. Equation

4 shows the cross correlation function where M and

N are the dimensions of the picture. Figure 9 shows

the eye pattern.

(

)() ()(

)

fxy gxy fxygx my n

−−

,∗ , = , +,+

∑∑

(4)

Figure 9: Eye pattern

Thus, eye masks are generated admitting an

80% tolerance of the maximum correlation value.

When both masks are computed, final eyes positions

are obtained. Figure 10 represents the process, and

figure 11 shows the positions computed.

6.2 Mouth pattern localization

Mouth can be easier identified than eyes. First, the

original face rectangle is divided horizontally. Then,

the mouth’s edges are computed using a Laplacian

method (Gonzalez, 1992) showed in equation 5:

() () ()

fxy fxy fx

∂∂

,= ,+ ,

∂∂

(5)

Edges on the lateral sides of the image are ig-

nored and a fill algorithm is applied. This

morphological algorithm changes black points into

white when all pixels in D8 neighborhood are white

(Gonzalez, 1992), this process repeats itself up to the

point where no change occurs in the image.

FACE PATTERN DETECTION - An approach using neural networks

175

Figure 10: Cross correlation Method and final eyes position

Figure 11: Mouth segmentation method

Finally, if the bigger connected region is ex-

tracted, it will very likely to be the mouth, as shown

in figure 11.

6.3 Nose pattern localization

Although mouth and eyes detection could be done

independently, nose position would be very difficult

to be found without the eyes and mouth information.

This happens because the nose usually does not have

detectable borders and is not, in general, darker or

brighter than the rest of the face.

However, if eye and mouth positions are

known, it is very likely that nose will be located

inside the rectangle defined by the centroids of both

eyes, mouth, and the lowest coordinate of eyes cen-

troid, as shown in figure 12.

Figure 12: Nose position.

From this region, the nose is segmented using

the same method of mouth detection of section 6.2,

by eliminating lateral edges and looking for the

bigger connected region filled by an morphological

algorithm.

7 RESULTS

With face localization methods described in sections

3, 4, 5 and face elements localization methods, de-

scribed in sections 6.1, 6.2 and 6.3; it is possible to

build a face pattern finder.

Using this pattern finder, 400 pattern-tests are

made using the faces available at the AT&T labora-

tory page (AT&T, 2003). Although the focal

distance variance among the faces is very small in

this database, it presents some other important chal-

lenges such as the presence of many non-frontal

poses and rotated faces.

Preliminary results, shown in table 1, indicate

that the most difficult task is nose identification,

because it has neither borders nor different colors

from the rest of the face elements, and it is also very

affected by the presence of glasses, beard or mus-

taches.

A comparison between the method present here

and two other are also shown in table 1:

The first one uses a spikenet to detect face pat-

terns (Van Rullen, 2001). The database used was the

same, but has been separated in test and train sets,

table 1 shows both results.

The Second one uses a Kiosk System (Mãkinen

et al, 2002) to detect face features, only frontal and

non-rotated faces were used.

Figure 13 shows various outputs from the sys-

tem. Face detection is shown in yellow; mouth

position in blue, eyes in red and finally nose in

white.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

176

Figure 13: Results of the Face pattern recognition system

Table 1: Preliminary comparative Results

Success rate

Element

Localization

Methods

This paper

(spikenet, 2001)

(Mãkinen et al, 2002)

Face Preprocessing, Illumination correction and ANN.

90% 88% 92%

Eyes 2d correlation with eyes pattern. 83% 90% 83%

Nose Edge detection and connected regions. 68% Not available 72%

Mouth Edge detection and connected regions. 86% 91% 47%

The same database (AT&T, 2003) was used as a training and test set, training set results are shown here.

Only frontal and non-rotated faces were used in these results.

8 CONCLUSIONS AND FUTURE

WORK

Results demonstrated on table 1 and figure 13 are

promising. Localization of eyes, mouth and face are

relatively well accurate, but nose position is quite

difficult to find because there are almost no features

that separates it from the background.

Face identity recognition systems can be im-

plemented using face localization methods shown

here. If face position is known, eyes and mouth

position can be found and used to adjust the orienta-

tion of the image. A new set of features can now be

extracted from these parts and used to feed another

neural network model trained to identify the owner

of the face.

New studies are being developed using the face

detection system presented in this paper. Then, it

will be possible to enhance detection process speed

and accurateness, in order to become a part of an-

other identity recognition system.

REFERENCES

Haykin, S., 1999. Neural Networks, a comprehensive

Foundation, 2

edition. Prentice Hall Press, New Jer-

sey.

Rowley, H., 1999. Neural Network-Based Face Detection.

School of Computer Science, Computer Science De-

partment, Carnegie Mellon University Pittsburgh.

Gonzalez, R. C., 1992. Digital Image Processing, Addi-

son-Wesley.

Zurada, J. M., 1992. Introduction to Artificial Neural

Systems, West Publishing Company, New York.

AT&T, 2003. AT&T Laboratories, Cambridge University

Engineering Department, Cambridge,

http://www.uk.research.att.com.

Johnson, R. 1998. Applied Multivariate Statistical Analy-

sis, Prentice-Hall, EUA, 1998.

Demuth, H. and Beale M. 2001. Neural Network Matlab

Toolbox, user’s guide. MathWorks, Inc.

Warren, S. 2001. Internet Neural Network

FAQ.ftp://ftp.sas.com/pub/neural/FAQ.html. Copy-

right 1997, 1998, 1999, 2000, 2001 by Warren S.

Sarle, Cary, NC, USA, 2001.

Mäkinen et al, 2002. Real-Time Face Detection for Kiosk

Interfaces. Unit for Computer-Human Interaction

(TAUCHI) Department of Computer and Information

Sciences FIN-33014 University of Tampere, Finland.

Van Rullen, 2002. FACE PROCESSING USING ONE

SPIKE PER NEURONE. Centre de Recherche

Cerveau & Cognition, UMR 5549, 133 route de Nar-

bonne, 31062 Toulouse, France.

FACE PATTERN DETECTION - An approach using neural networks

177