ENHANCING THE SUCCESS RATIO OF DISTRIBUTED

REAL-TIME NESTED TRANSACTIONS

M. Abdouli, B. Sadeg, L. Amanton and A. Berred

Laboratoires LIH, LMAH, UFR des Sciences et Techniques du Havre,

25 rue P. Lebon, BP 540, 76058 Le Havre cedex, FRANCE

Key words: Nested Transaction, Distribu

ted System, Concurrency Control, RTDBS

Abstract: The traditional transaction models are not suited to real-time database systems (RT

DBSs). Indeed, many

current applications managed by these systems necessitate a kind of transactions where some of the ACID

properties must be ignored or adapted. In this paper, we propose a real-time concurrency control protocol

and an adaptation of the Two-Phase Commit Protocol based on the nested transaction model where a nested

transaction is viewed as a collection of both essential and non-essential subtransactions: the essential

subtransaction has a firm

deadline, and the non-essential one has a soft

deadline. We show through

simulation results, how our protocol based on this assumption, allows better concurrency between

transactions and between subtransactions of the same transaction, enhancing then the success ratio

and the

RTDBS performances, i.e., more transactions may meet their deadlines.

The authors would like to thank the French Research Ministry and the University of Le Havre for their financial support

(ACI No 1055 and RTT project, respectively).

Atomicity, Consistency, Isolation, Durability

A transaction is aborted as soon as it misses its deadline

A transaction may provide useful results after its deadline, but the Quality of Service (QoS) decreases

Number of transactions that meet their deadline/Total number of transactions

1 INTRODUCTION

RTDBSs are generally defined as the database

systems supporting time-constrained transactions.

The timing constraints are usually expressed in the

form of transaction deadlines. The first requirement

in RTDBSs is to maintain the database consistency

by enforcing the concurrency control between the

active transactions. The second requirement is to

satisfy the real-time constraints of the transactions in

order to meet their individual deadlines. In the

earlier models of traditional RTDBSs, a transaction

is considered as a single flat unit of tasks [Haritsa

and Ramamritham, 1997, Ramamritham, 1993],

which consists of a sequence of primitive actions

(e.g., read and write of data-items). If one operation

of the transaction fails, then the whole work done by

transaction is rolled-back. Most of the previous

work [Bernstein and Goodman, 1987, Krzyzagorski

and Morzy, 1995] on RTDBSs have used flat

transaction as the underlying transaction model, but

these approaches are not suitable to many new

database applications. Some applications have

changed from traditional applications to more

advanced and complex applications, such as

computer aided design (CAD), cooperative

applications and multimedia applications.

The nested transaction model, originally

troduced to increase transaction reliability in

distributed systems [Moss, 1986], is proved to be

more appropriate for these new applications. The

first nested transaction model has been proposed by

Moss [Moss, 1986]. A nested transaction is

considered as a hierarchy of subtransactions, and

each subtransaction may contain either other

subtransactions, or the atomic database operations

(read or write). Furthermore, a nested transaction is

233

Abdouli M., Sadeg B., Amanton L. and Berred A. (2004).

ENHANCING THE SUCCESS RATIO OF DISTRIBUTED REAL-TIME NESTED TRANSACTIONS.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 233-240

DOI: 10.5220/0002615002330240

 SciTePress

a collection of subtransactions that compose the

whole atomic execution unit.

A nested transaction is represented as a tree,

called transaction tree [Moss, 1986, Chen and

Gruenwald, 1994, El-Sayed and El-Sharkawi, 2001,

Reddy and Kitsuregawa, 2000]. A nested transaction

offers more decomposable execution units and finer

grained control over concurrency and recovery than

flat transaction. Nested transactions provide intra-

parallelism, (subtransactions running in parallel) as

well as better failure recovery options, i.e., when a

subtransaction fails and aborts, there is a chance to

restart it by its parent instead of restarting the whole

transaction (which is the case of flat transactions).

Even though, the major driving force in using nested

transaction is the need to model long-lived

applications, nested transactions may also be

efficiently used to model short transactions (like in

the context of real-time database applications, with

specific characteristics).

The main performance goal of RTDBSs

scheduling notably for firm and soft transaction is to

minimize the number of transactions that miss their

deadlines. So, a performance metric in assessing the

system performance in RTDBMSs is the

"throughput". Throughput is defined in terms of the

number of transactions that complete successfully,

which is also called the "success ratio". A

transaction is considered to be successfully

completed if it runs completely and commits its

result before its deadline.

When multiple users access a database

simultaneously, their data operations have to be

coordinated in order to prevent incorrect results and

to preserve the shared data consistency. This

activity is called concurrency control [Abbott, 1988,

Pavlova and Nekrestyanov, 1997], which has always

been a major aspect of computing systems. In recent

years, different real-time concurrency control

protocols have been proposed to both flat and nested

transactions. In this paper, we consider the case of

nested transactions model and its application to real-

time transactions.

The remaining of this paper is organized as

follows. In the next Section, we describe a kind of

nested transactions models. In Section 3, we present

some real-time concurrency control protocols for

nested transactions and we introduce our

concurrency control protocol for real-time nested

transactions. The protocol implementation is

described in Section 4 with some simulation results.

Finally, in Section 5, we conclude and give some

future research directions.

2 NESTED TRANSACTION

MODELS

The main types of the various models of nested

transactions are (1) closed nested transaction [Moss,

1986] and (2) open nested transaction [Madria and

Bhargava, 2000]. In the closed nested transaction

model [Moss, 1986, El-Sated and El-Sharkawi,

2001], a subtransaction’s effect cannot be seen

outside its parent’s view. Originally introduced by

Moss [Moss, 1986], a commitment of a

subtransaction is conditional upon the commitments

of its parent, while in the open nested transaction

model [Madria and Bhargava, 2000], the

subtransactions can execute and commit

independently. The model provides non-strict

execution by taking into account the commutative

properties of the semantics of the operations at each

level of data abstraction. A subtransaction is

allowed to release its locks before the higher-level

transaction has committed. The leaf level locks are

released early only if the semantics of the operations

is known. In many applications, the semantics of

transactions cannot be known and hence, it is

difficult to provide non-strict execution. So, in this

paper, we consider a closed nested transaction

model. Nested transaction extends the flat

transaction by allowing a transaction to invoke

atomic transactions as well as atomic operations. In

a nested transaction model, a transaction may

contain any number of subtransactions, which again

may be composed of any number of subtransactions,

conceivably resulting in an arbitrary deep hierarchy

of nested transactions.

The root transaction, which is not enclosed in

any transaction, is called the top-level transaction

(TLT). Transactions having subtransactions are

called parent transactions (PTs), and their

subtransactions are their children. Leaf transactions

(LTs) are those transactions with no child.

The ancestor (resp. descendant) relation is the

reflexive transitive closure of the parent (resp.

child) relation. We will use the term superior (resp.

inferior) for the non-reflexive version of the ancestor

(resp. descendant). The children of one parent are

called siblings. The set of descendants of a

transaction together with their parent/child

relationships is called the transaction’s hierarchy.

The hierarchy of a TLT can be represented by a so-

called transaction tree. The nodes of the tree

represent PTs, and the edges illustrate the

parent/child relationships between the related

transactions. In the transaction tree shown in

Figure.1, T1 represents TLT or root.

– T1 is a root or TLT,

– T2 and T3 are children of T1,

ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

234

– T2 and T3 are siblings,

– T4 and T5 are children of T2,

– T8,T9,T5,T6 and T7 are leaf transactions,

– T8’s ancestors are T1,T2,T4 and T8,

– T8’s superiors are T1,T2 and T4,

– T2’s descendants are T8,T9,T4,T5 and T2,

– T2’s inferiors are T8,T9,T4 and T5.

Figure 1: Example of Transaction Tree

In the nested transaction model, N-ACID

properties are fulfilled for top-level transactions,

while only a subset of them are defined for

subtransactions. Subtransactions appear atomic to

the surrounding transactions and may commit and

abort independently. A transaction is not allowed to

commit until all its children have terminated.

However, if a child is aborted or fails, their parent is

not required to abort. Instead, the parent is allowed

to perform its own recovery. In order to meet its

goal, the parent may choose one of the following

actions [Moss, 1986, Chen and Gruenwald, 1994] :

(1) to ignore the condition, (2) to retry the

subtransaction, (3) to initiate another subtransaction

that implements an alternative action, (4) to abort the

subtransaction.

The durability of the committed subtransaction

effects depends on the outcome of its superiors.

Even if a subtransaction commits, the abort of one of

its superiors will undo its effects. The updates of a

subtransaction become permanent only when the

enclosing TLT commits. In the nested transaction

model defined in [Moss, 1986], the work can only be

done by the leaf-level transactions. Higher level

transaction only organizes the control flow and

determines when to invoke which subtransaction.

Two main differences exist between the various

models of nested transactions [Guerraoui, 1995]: (1)

whether or not a parent can directly access a data-

item and (2) whether or not it can execute

concurrently with its children. In this paper, we

consider only the model where such accesses are

reserved only to leaf transactions.

3 REAL-TIME CONCURRENCY

CONTROL PROTOCOLS

3.1 Towards existing protocols

Several protocols are used for synchronizing the

execution of nested transactions and therefore for

ensuring isolated execution of transactions. A

number of concurrency control algorithms are

proposed in the literature and used widely.

Concurrency control protocols may be divided into

two groups [Abbott, 1988, Krzyzagorski and Morzy,

1995, Pavlova and Nekrestyanov, 1997]: (1)

optimistic and (2) pessimistic approaches. The main

feature of the pessimistic approach is to prevent

possible conflicts. A transaction may access a data-

item only if this will not cause possible conflict

situations later. If it is not possible immediately, the

transaction should wait until it becomes possible.

Most pessimistic algorithms are based on locks

[Bernstein and Goodman, 1987, Harder and

Rothermel, 1993, Resende and Abbadi, 1994]. The

classical pessimistic algorithm is the widely used

two phase locking (2PL) protocol and its variants,

such as 2PL-HP [Chen and Gruenwald, 1994 and

Pavlova and Nekrestyanov, 1997]. In nested

transaction model, 2PL is an upward inheritance of

locks [Harder and Rothermel, 1993]. There exist

other protocols using the same approach such as:

priority abort protocol [Chen and Gruenwald, 1994]

and priority inheritance protocol [Bernstein and

Goodman, 1987]. In [Harder and Rothermel, 1993],

a concept of downward inheritance is introduced to

improve the parallelism within the nested

transaction. The pre-write operation is introduced in

[Madria and Bhargava, 2000] to increase

concurrency in a nested transaction processing

environment. This model allows some particular

subtransactions to release their locks before their

ancestor transaction commits.

In optimistic approach [Krzyzagorski and

Morzy, 1995], transaction execution consists of

three phases: read, validation and write. During the

read phase, transactions work in parallel without any

verification and each transaction writes to its own

space. The validation phase consists of the

checking-up of the existing conflicts. After a

successful validation, it is possible to commit the

transaction and to copy its local space to the

database. In the last few years, some researches that

merge both optimistic and pessimistic distributed

approaches have been done, such as hybrid

concurrency control for the nested transaction

proposed in [Pavlova and Nekrestyanov, 1997]. This

ENHANCING THE SUCCESS RATIO OF DISTRIBUTED REAL-TIME NESTED TRANSACTIONS

235

protocol acts as an optimistic protocol for

transactions from different transaction trees and as

pessimistic protocol inside a single transaction tree.

In [Reddy and Kitsuregawa, 2000] the speculative

nested locking protocol is proposed. In speculative

nested transaction approach, a (sub)transaction

releases a lock on the data-item when it produces

after-image. In this approach a transaction carries

out multiple executions by reading both before-

image and after-image of the preceding transaction.

In this section, we review the basic two-phase

locking protocol for nested transaction (2PL-NT).

We begin to explain some used terms and we

sumarize this mechanism in the following.

– R-mode: Read mode, shared mode,

– W-mode: Write mode, exclusive mode.

R1 : T may acquire a lock in R-mode if

– no other transaction holds the lock in

W-mode, and

– all transactions that retain the lock

in W-mode are its ancestors.

R2 : T may acquire a lock in W-mode if

– no other transaction holds the lock

in W- or R-mode, and

– all transactions that retain the lock

in W- or R-mode are its ancestors.

R3 : When T commits, its parent inherits its

(held or retained) locks. After that, T’s

parent retains the locks in the same mode

(W or R) in which T has hold or retained

the locks previously.

R4 : When T aborts, it releases all locks it

holds or retains. If any of its superiors

holds or retains any of these locks, then

continue to do so.

If a top-level transaction commits, then all its locks

are released.

Note that the inheritance may cause a

transaction to retain several locks on the same

object.

3.2 Motivation

In our model, nested transaction consists of both

essential and non-essential subtransactions. If an

essential subtransaction aborts, the rest of the

transaction has to be aborted, whereas, aborting a

non-essential subtransaction is allowed. It should be

noted that a non-essential subtransaction could block

the essential subtransaction by holding the crucial

lock. Since, each subtransaction acts as a unit of

work to complete for resources, then, it should

possess its own deadline. Deadline assignment for

subtransactions is beyond the purpose of this paper.

So far, we assume that each subtransaction has a

deadline. Then, we assume that an essential

subtransaction is firm and a non-essential

subtransaction is soft. In that case, the whole time is

given to the essential transaction since (1) the non-

essential transaction’s missing deadline is not fatal,

(2) the non-essential transaction’s shorter deadline

may increase its priority and possibly finish earlier,

increasing the essential transaction’s chance to meet

its deadline. To illustrate our model, we will use as

an example of a control/display system. This system

gives us a clear idea on the concept of essential and

non-essential transactions.

For example, the Control subtransaction may be

declared as essential. If a Control subtransaction

commits, the nested transaction does so. However,

if the display subtransaction cannot be committed,

then the Control/Display nested transaction may still

successfully complete.

3.3 Our protocol

In this section, we describe our protocol and give an

example that shows how the inter-transactions and

intra-transactions concurrency are increased, which

improves the objective of RTDBMS. In our

approach, the locking protocol offers 4 modes of

synchronizations:

– The (ER-mode): Essential Read,

– The (EW-mode): Essential Write,

– The (NER-mode): Non-Essential Read,

– The (NEW-mode): Non-Essential Write.

Our protocol adapted from the basic 2PL-NT

provides the following rules.

Rule 1: If T is an essential transaction:

a) T may acquire a lock in ER-mode if

– No other transaction holds the

lock in EW-mode, and

– All transactions that retain the

lock in EW-mode are its

ancestors.

b) T may acquire a lock in EW-mode if

– No other transaction holds the

lock in EW- or ER-mode, and

– All transactions that retain the

lock in EW- or ER-mode are

its ancestors.

Rule 2: If T is a non-essential transaction

a) T may acquire a lock in NER

-mode if

– No other transaction that

holds the lock in EW- and

NEW-mode, and

– All transactions that retain the

lock in NEW- mode are its

ancestors.

b) T may acquire a lock in NEW if

– No other transaction holds the

lock in EW-, NEW-, ER- and

NER-mode

ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

236

– All transactions that retain the

lock in NEW- or NEW-mode

are its ancestors.

Rule 3: When T commits, its parent

inherits its (held or retained) locks. After

that, T’s parent retains the lock in the same

mode in which T held or retained the lock

previously.

Rule 4: When T aborts, it releases all helds

or retained locks. If any of its superiors

holds or retains any of these locks, then they

continue to do so.

The ER-mode permits multiple transactions to

share a data-item. Furthermore, an essential and

non-essential transaction could acquire the lock at a

time. If a non-essential transaction holds a lock in

NEW-mode while an essential transaction requests a

lock in ER-mode on the same data-item, then the

conflict is resolved in favor of the essential

transaction and the non-essential transaction is

aborted and restarted. If an essential transaction

requests a lock in EW-mode on the same data-item,

then all conflicts with a non-essential transaction are

resolved in favor of the essential transaction. A

retained EW-, ER-, NEW- and NER-locks, indicate

that transactions outside the hierarchy of the retainer

can not acquire the lock, but the descendants of the

retainer potentially can do, i.e., if a transaction T

retains an EW-lock, then all non-descendants of T

cannot hold the lock in any mode (EW or ER). Table

1 shows the compatibility matrix between requesting

and locking modes. The rows are the holding locks,

and the columns are the requested locks.

Table 1: Compatibility matrix

3.3.1 Example 1

In the following example and for the simplicity

reasons, we assume that the runtime for a write or a

read operation is 10 seconds. Every subtransaction

is characterized by its arrival time and its own

deadline. If a subtransaction is essential then its

deadline is firm, otherwise it is soft. We will use

both protocols (a basic 2PL-NT and our protocol) to

the same example in order to illustrate the

performance of our protocol. For a basic 2PL-NT,

all subtransactions are assumed to be essential.

Figure 2: T2: essential subtransaction,

T3: non-essential subtransaction,

Nested transaction model increases intra-transactions

concurrency

Figures 2 and 3 summarize the example for a basic

2PL-NT (in this case, all subtransactions in Figure 2

are essential).

– At t=0, T3 acquires and obtains a lock in W-

mode on a data-item v,

– 3s afterward, T4 appears. It is blocked until

the termination of T3. As its deadline is at

15s then it misses its deadline and aborts.

Then the top-level transaction does so.

Figure 3: Scheduling in the basic 2PL-NT (example 1)

Figures 2 and 4 summarize the example with our

protocol.

All transaction that retain

the lock are its ancestors

All transaction that retain

the lock are not its ancestors

ER EW NER NEW ER EW NER NEW

ER Yes Yes -- -- Yes No Yes Yes

EW Yes Yes -- -- No No Yes Yes

NER -- -- Yes Yes No No Yes No

NEW -- -- Yes Yes No No No No

– T3 runs until the arrival of T4,

– T4 obtains a lock on the data-item v in EW-

mode,

– T3 aborts,

– T4 meets its deadline,

– T3 is restarted, as its deadline is soft,

completes its execution but the quality of

service (QoS) decreases,

– The top-level transaction may choose

between the following two cases for the

commitment:

(a) Commit as soon as T4 commits (if a

conflict may exist with other essential

subtransactions),

(b) Commit after the termination of T3.

ENHANCING THE SUCCESS RATIO OF DISTRIBUTED REAL-TIME NESTED TRANSACTIONS

237

Figure 4: Scheduling mechanism in our protocol

(example 1)

3.3.2 Example 2

Figures 5 and 6 summarize the example for a basic

2PL-NT (in this case, all subtransactions in Figure 5

are essential).

– At first, T3 requests and obtains a lock in W-

mode on data-item u,

– 3s afterward, T7 is initiated and is blocked (it

requests a lock held by T3) until termination

of T3. Consequently, it can not meet its

deadline,

– T7 aborts and the top-level transaction does

so.

Figure 5: T2 and T7: essential subtransactions, T3 and T8:

non-essential subtransactions,

Nested transaction model increases concurrency inter-

transactions.

Figure 6: Scheduling in the basic 2PL-NT (example 2)

Figures 5 and 7 summarize the example for our

protocol.

Figure 7

: Scheduling mechanism in our protocol

(example 2)

In this way, our protocol increases both inter- and

intra-transactions concurrency of nested

transactions.

4 IMPLEMENTATION

In this paper, we have used an adaptation of the

Two-Phase Commit protocol. Briefly, the 2PC

protocol consists of Voting and Completion

according phase to the outcome of vote. For more

details see [Haritsa and Ramamritham, 2000].

4.1 Basic functionalities

Recall that the nested transaction consists of the

TLT, PT and LT. Both TLT and PT need a

coordinator. A coordinator for a subtransaction will

provide an operation to open a subtransaction. The

coordinator of the TLT communicates with the

coordinators of the subtransactions for which it’s the

immediate parent. In the first phase of the 2PC

protocol, each coordinator sends CanCommit

message to each of later, with in turn passes them to

the coordinators of their child transaction (and so on,

down the tree). Note that each TLT is characterized

by its identifier TID. Thus each subtransaction

possesses its own identifier that must be an

extension of its parent’s TID. Therefore, the

coordinator of each parent transaction has a list of its

children. When a nested transaction provisionnally

commits, it reports its status and the status of its

descendants to its parent. Eventually, the TLT

receives a list of all the subtransactions in the tree,

together with the status of them. The TLT plays the

role of the coordinator in the 2PC, and the

participant list consists of the coordinators of all

subtransactions in the tree which have

provisionnally committed and that not have aborted

ancestors. These participants will ask to vote on the

outcome. If they vote to commit, then they must

prepare their transactions by saving the state of the

data in the permanent storage.

The second phase of the 2PC is the same as for

the non-nested case, but it must be adapted for our

model. The coordinator collects the votes and then

informs the participants:

1. If all essential subtransactions and non-

essential subtransactions vote YES, the

coordinator and the participants will be

committed,

2. If one or more essential subtransactions votes

NO, then the TLT aborts its subtransactions,

3. If all essential subtransactions vote YES and

one or more non-essential subtransactions

vote NO, then the coordinator according its

ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

238

deadline and the eventual conflicts with

essential subtransactions in other transaction

tree, chooses between the following two

cases :

(a) To commit the essential

subtransactions and to abort the non-

essential subtransactions, or

(b) To commit after the termination of

the non-essential subtransactions ( in

this case, the QoS decreases).

4.2 Simulation results

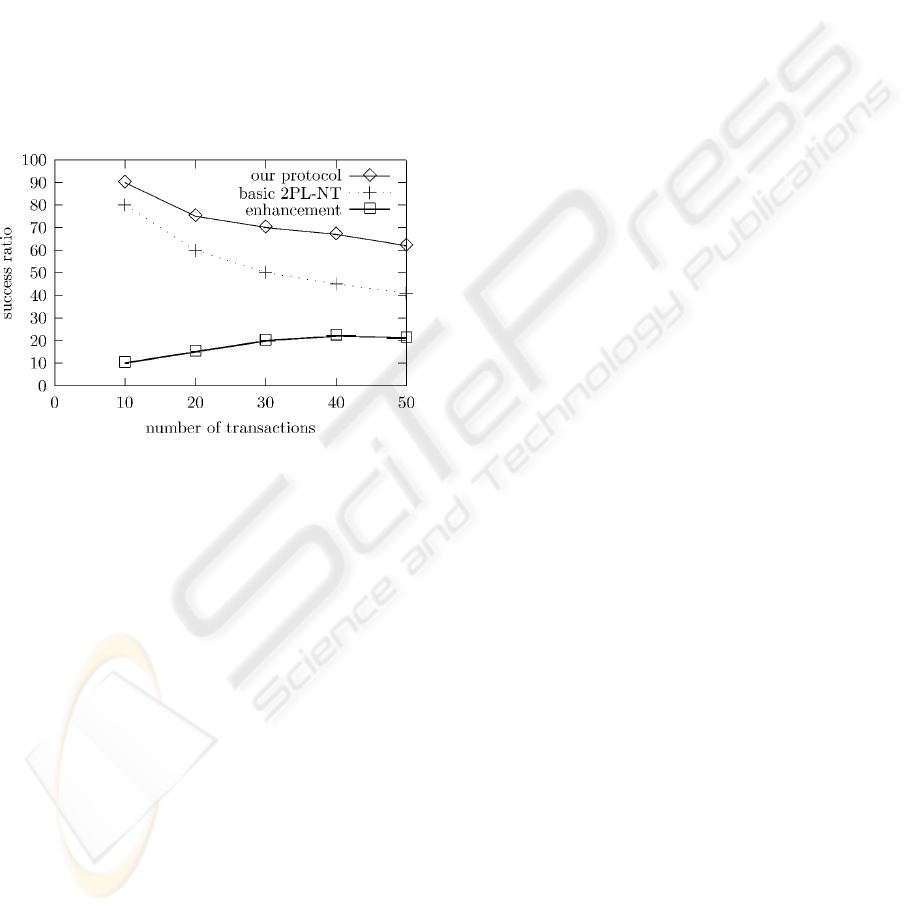
Simulation results show that the success ratio is

better when using the new protocol than when using

the basic 2PL-NT (see Figure8). The enhancement is

about 17%.

Figure 8: Our protocol vs the basic 2PL-NT

Even though, we notice that the proposed

algorithm presents some restrictions (because it does

not authorize the serialization between the essential

and non-essential transactions). Our approach

compared to the basic nested transaction enhances

the success ratio. Hence, this algorithm seems more

advantageous for real-time applications.

Furthermore, our approach allows the adaptation of

the N-ACID properties for real-time context. For

instance, the top-level transaction does not satisfy

the Atomicity property because if a non-essential

transaction fails then it does not force its parent to

do so. Therefore, only the N-CID properties are

fulfilled for top-level transaction in our work. In

addition, the effects of subtransaction do not become

permanent until its top level transaction commits.

Thus, a subtransaction does not satisfy the durability

property.

In summary, the simulation results show the

usefulness of our assumptions, allowing more

transactions to meet their deadlines.

5 CONCLUSION AND FUTURE

WORK

In this paper, we have proposed a concurrency

control protocol approach based on 2PL and an

adaptation of the 2PC protocol for nested transaction

model in real-time systems. We have focused on

achieving a high degree of both inter-transactions

and intra-transaction concurrency within nested

transactions. In the proposed model, each

transaction is composed of both essential and non-

essential (sub)transactions. When a conflict appears,

it is resolved in favor of the essential

(sub)transaction. If an essential transaction aborts,

then the rest of the transaction has to be aborted.

However, if a non-essential transaction cannot

commit, then the nested transaction can still be

successfully completed.

In a nested transaction model, if a parent

transaction aborts, then all its children do so. To

enhance the degree of intra-transactions parallelism,

for the future work we will use the PROMPT

protocol mechanism [Haritsa and Ramamritham,

2000] which was used for flat transactions and

where the isolation property is relaxed, it allows the

lending of data by uncommited transaction, and

using a probabilistic model to analyze the real-time

nested transactions. The obtained probabilistic

model would allow to determine weights to assign to

subtransactions and to determine the threshold value

which indicate whether the subtransaction is

essential or not.

REFERENCES

A.A. El-Sayed, H. H. and El-Sharkawi, M. (2001). it

effects of shaping characteristics on the performance

on nested transactions. Information and Software

Technology, 43: 579–590.

Chen, Y. and Gruenwald, L. (1994). Research issues for a

real-time nested transaction. In 2nd Workshop on

Real-Time Applications, pages 130–135.

Guerraoui, R. (1995). Nested transaction : Reviewing the

coherence contract. Elsevier Sciences, 84: 161–172.

Harder, D. and Rothermel, D. (1993). Concurrency control

issues in nested transactions. VLDB journal, 2(1): 74–

93.

Harista, J. and Ramamritham, K. (1997). Real-time

database systems in the new millenium. Real-Time

Systems Journal, 19(3).

Haritsa, J. and Ramamritham, K. (2000). The prompt real-

time commit protocol. IEEE Transactions on Parallel

and Distributed Systems, 11(2).

ENHANCING THE SUCCESS RATIO OF DISTRIBUTED REAL-TIME NESTED TRANSACTIONS

239

Krzyzagorski, P. and Morzy, T. (1995). Optimistic

concurrency algorithm with dynamic serialization

adjustment for firm deadline real-time datadase

system. In 2nd International Workshop on advances in

Databases and Information Systems, volume 1, pages

21–28.

Moss, J. (1986). Nested Transactions: an Approach to

Reliable Distributed Computing. PhD thesis,

University of Massachusetts.

P.A. Bernstein, V. H. and Goodman, N. (1987).

Concurrency Control and Recovery in Database

Systems. Addison - Wesley.

Pavlova, E. and Nekrestyanov, I. (1997). Concurrency

control protocol for nested transactions in real-time

databases. In First East-European Symposium on

Advances in Databases and Information Systems, St-

Petersbur.

R. Abbot, G.-M. (1988). Scheduling real-time

transactions: a performance evaluation. In 14th

international conference on VLDB, pages 1–12.

Ramamritham, K. (1993). Real-time databases.

Distributed and Parallel Databases, 1(2).

Reddy, P. K. and Kitsuregawa, M. (2000). Speculation

based nested locking protocol to increase the

concurrency of nested transactions. In Press, I., editor,

International Database Engineering and Application

symposium, pages 18–28, Yokohama, Japan.

Resende, R. and Abbadi, A. (1994). On the serializability

theorem for nested transactions. Information

Processing Letters, 50(4).

S.K. Madria, S.N. Maheshwari, B. C. and Bhargava, B.

(2000). An open and safe nested transaction model:

Concurrency and recover. System and Software, 55:

151–165.

ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

240