
DYNAMIC DIAGNOSIS OF ACTIVE SYSTEMS WITH
FRAGMENTED OBSERVATIONS
Gianfranco Lamperti
Dipartimento di Elettronica per l’Automazione
Via Branze 38, 25123 Brescia, Italy
Marina Zanella
Dipartimento di Elettronica per l’Automazione
Via Branze 38, 25123 Brescia, Italy
Keywords:
Knowledge-based systems engineering, model-based reasoning, diagnosis, discrete-event systems,
active systems, communicating automata, monitoring, uncertainty
Abstract:
Diagnosis of discrete-event systems (DESs) is a complex and challenging task. Typical application
domains include telecommunication networks, power networks, and digital-hardware networks.
Recent blackouts in northern America and southern Europe offer evidence for the claim that auto-
mated diagnosis of large-scale DESs is a major requirement for the reliability of this sort of critical
systems. The paper is meant as a little step toward this direction. A technique for the dynamic
diagnosis of active systems with uncertain observations is presented. The essential contribution of
the method lies in its ability to cope with uncertainty conditions while monitoring the systems,
by generating diagnostic information at the occurrence of each newly-received fragment of obser-
vation. Uncertainty stems, on the one hand, from the complexity and distribution of the systems,
where noise may affect the communication channels between the system and the control rooms, on
the other, from the multiplicity of such channels, which is bound to relax the absolute temporal
ordering of the observable events generated by the system during operation. The solution of these
diagnostic problems requires nonmonotonic reasoning, where estimates of the system state and the
relevant candidate diagnoses may not survive the occurrence of new observation fragments.
1 INTRODUCTION
Diagnosis is the task of finding out the faults af-
fecting a physical system given a set of symptoms
gathered by observing the system itself. Model-
based diagnosis is a research area in Artificial In-
telligence devoted to proposing automated rea-
soning mechanisms and modeling primitives for
performing such a task by exploiting the (struc-
ture and behavior) models of the considered phys-
ical systems. From the middle ’90s some research
efforts have been directed toward model-based di-
agnosis of DESs since discrete models are simpler
to deal with than continuous ones (Fattah and
Provan, 1997; Debouk et al., 2000; Lunze, 2000;
Cordier and Largou¨et, 2001; Pencol´e et al., 2001;
Console et al., 2002) .
Diagnostic processing can be carried out either
after an observation has been collected through-
out a time interval or every time a new observ-
able event is received. In order to distinguish the
two situations we call a posteriori diagnosis the
former task and dynamic (or monitoring-based)
diagnosis the latter.
This paper deals with dynamic diagnosis of ac-
tive systems (Lamperti and Zanella, 2003b). In-
terest on active systems was prompted by the case
study of diagnosis of power transmission networks
(Lamperti and Pogliano, 1997), aimed at prevent-
ing blackouts. Such networks are still a reference
application domain although the notion of an ac-
tive system has progressively been generalized so
as to represent a large class of DESs. The con-
cept of a fragmented observation taken as input
by the task described in this paper is more general
than any one by other authors, corresponding to
an uncertain observation, as defined in (Lamperti
and Zanella, 2002). The only difference between
an uncertain and a fragmented observation is that
the former cumulatively represents all the observ-
able events received over a time interval while
the latter represents a single (logically uncertain
and/or temporally uncertain and/or source un-
certain) observable event, called a message.
249
Lamperti G. and Zanella M. (2004).
DYNAMIC DIAGNOSIS OF ACTIVE SYSTEMS WITH FRAGMENTED OBSERVATIONS.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 249-261
DOI: 10.5220/0002619202490261
Copyright
c
SciTePress

Past research has focused both on a posteriori
diagnosis (Baroni et al., 1999) and dynamic di-
agnosis (Lamperti and Zanella, 2003a) of active
systems. However, uncertain observations have
so far been provided as input to a posteriori diag-
nosis while dynamic diagnosis had been fed only
by completely certain observations. No contribu-
tion in the literature to monitoring and diagno-
sis of DESs takes into account observable events
that are uncertain in nature. The purpose of the
present work is to face this challenge.
In the remainder of the paper, Section 2
presents the context from which all the examples
in the paper are drawn. Section 3 provides a for-
mal definition of the class of considered systems.
Section 4 defines the class of problems inherent
to such systems that can be solved by the tech-
nique described in Section 5. Section 6 relates the
current work to other works in the literature and
concludes the paper.
2 POWER NETWORK
We consider a sample application domain involv-
ing power networks. Each transmission line is
protected by two breakers that are commanded
by a protection. The protection is designed to
detect conditions that may be dangerous to the
line. Typically, if a short circuit affects the line,
the protection is expected to command the two
breakers to open, so as to isolate the line from
the remaining part of the network. In a simpli-
fied view, the network is represented by a series
of lines, each one associated with a protection, as
displayed in Fig. 1.
The figure outlines a portion of the network,
that encompasses two lines, L
1
and L
2
, with rel-
evant protections, p
1
and p
2
. For instance, p
2
controls L
2
by operating breakers b
21
and b
22
. In
normal behavior, both breakers are expected to
open when tripped by the protection. However,
the protection system may exhibit an abnormal
(faulty) behavior, for example, one breaker or
both may not open when required. In such a case,
each faulty breaker informs the protection about
its own misbehavior. Then, the protection sends
a request of recovery actions to the neighboring
protections, which will operate their own break-
ers appropriately. For example, if p
2
operates b
21
and b
22
and the former is faulty, then p
2
will send
a signal to p
1
, which is supposed to command
the breaker on the same (left-hand) side of the
faulty breaker b
21
, namely b
11
. If both b
21
and
b
22
are faulty, then p
2
will ask recovery actions
to both the neighboring protections. The protec-
Figure 1: Power network.
tion system is designed to propagate the recovery
request until the tripped breaker opens correctly.
Consequently, the greater the number of faulty
breakers, the larger the extent of the subnetwork
that is isolated.
When the protection system reacts to a short
circuit by attempting to isolate the shorted line,
possibly with the help of recovery actions, a sub-
set of the occurring events are visible to the ex-
ternal world, typically to the operator of a control
room who is in charge of monitoring the behavior
of the network and, possibly, to perform actions
so as to minimize the extent of the isolated sub-
network by means of explicit telecommands. In
the ideal scenario, the reaction of the protection
system is correct (normal) and the shorted line
is clearly identified by the pair of open breakers.
So, if the operator observes that b
21
and b
22
are
open, he or she is allowed to assume that line L
2
has been isolated owing to a short circuit. If the
short circuit is transient (caused, for example, by
a lightning), it may be the case that, once the
short has extinguished, the isolated line is recon-
nected to the network by the operator. If such a
reconnection is successful (no reaction of the pro-
tection system is triggered anew), the network
keeps on being fully operating. Instead, if the
short circuit is permanent (for example, due to
a tree fallen on the line), the reconnection will
cause a new reaction of the protection system
1
.
The reconnection problem becomes harder
when the reaction of the protection system is ab-
normal. In fact, the operator is supposed to face
the additional problem of localizing the shorted
line among those embodied within the isolation.
Such an identification cannot be carried out by
simply looking at open breakers. With reference
to Fig. 1, if the open breakers are b
11
and b
22
,
then the shorted line will be either L
1
or L
2
. A
static analysis of the isolation does not provide
any clue on where the short circuit is located.
1
The protection system typically operates au-
tonomously in two steps. First, the shorted line is
isolated for a few seconds in the hope of extinguish-
ing the (transient) short circuit. Later, the line is re-
connected to the network and, if the short circuit has
extinguished, then the network is completely recov-
ered, otherwise the line is isolated permanently from
the system.
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
250

Assuming the occurrence of a single short cir-
cuit, the only possible claim is that one breaker
is faulty, corresponding to two different scenar-
ios. In the first scenario, L
1
is shorted and b
12
is
faulty, thereby requiring the intervention of b
22
.
The second scenario is symmetric: D
2
is shorted
and b
21
is faulty. In either case, one line is not
shorted and might be reconnected without any
risk (provided the operator knows which it is).
For instance, if the shorted line is L
1
, then L
2
can be reconnected to the network by opening
b
12
manually and telecommanding the closure of
b
22
.
The localization of the short circuit and the
identification of the faulty breakers may be im-
practical in real contexts, especially when the ex-
tent of the isolation spans several lines and the op-
erator is required to take recovery actions within
stringent time constraints. On the one hand,
there is the problem of observability: the observ-
able events generated during the reaction of the
protection system are generally incomplete and
uncertain in nature. On the other, whatever the
‘quality’ of the observation, it is practically im-
possible for the operator to reason on the obser-
vations under stringent time constraints, so as to
make consistent hypotheses on the behavior of the
system and, eventually, to establish the shorted
line and the faulty breakers.
The task of the operator might be dramatically
improved if we would provide a tool that supports
the automated reconstruction of the system reac-
tion and the generation of the expected informa-
tion, namely, the diagnosis of the system. This re-
quires the precise definition of the class of consid-
ered systems, namely active systems, along with a
specific diagnostic technique. We then show that
our network can be modeled as an active system
and, as such, automatically diagnosed by means
of the given technique.
3 ACTIVE SYSTEMS
A system is a network of components that are
connected to one another through links. Each
component is completely modeled by a commu-
nicating automaton C that reacts to events either
coming from the external world or from neigh-
boring components through links. Formally, the
automaton is a 7-tuple,
C = (S, E
in
, I, E
out
, O, T, P),
where S is the set of states, E
in
the set of input
events, I the set of input terminals, E
out
the set
of output events, O the set of output terminals, T
the nondeterministic transition function,
T : S × E
in
× I × 2
E
out
×O
7→ 2
S
,
and P the priority hierarchy. A transition T ∈ T,
from state S to state S
0
, that is triggered by
event e at input terminal I, and generates events
e
1
, . . . , e
k
at output terminals O
1
, . . . , O
k
, respec-
tively, is denoted by
T = S
(e,I)
−−−−−−−−−−−−→
(e
1
,O
1
),...,(e
k
,O
k
)
S
0
.
The priority hierarchy is a DAG where nodes are
events in E
in
×I, while edges denote a partial pri-
ority relationship among events. Since transitions
are triggered by input events, the priority hierar-
chy among events implicitly defines a priority hi-
erarchy among the transitions in T, specifically,
if T
1
has higher priority than T
2
, T
1
will be fired
before T
2
. Generally speaking, among the set of
triggerable transitions, the actual fired transition
will be one among those with highest priority.
Links, which are the means to store the events
exchanged between components, are modeled by
a triple
L = (I, O, M),
where I is the input terminal, O the output ter-
minal, and M the event management. The latter
establishes the internal structure of the link and
the effect of each newly inserted event. Given a
link L, the function Ready(L) returns the set of
(ready) events stored in L that can be consumed
in the current state of the link. For example, if the
event management is a queue, Ready(L) will be
the first event in the queue. By contrast, if M is
a stack, Ready(L) will be the last-inserted event.
With a more sophisticated management where
priorities are defined among events stored in L,
Ready(L) is bound to return several consumable
events. The priority hierarchy P of a component
and the event management M of a link L are
different, yet related, concepts: the priority re-
lationships in P are applied to those transitions
that are triggered by the events in Ready(L), the
latter depending on M . Since the input terminals
of a component may be connected with a set L
c
of links, the whole set of consumable events is de-
noted by Ready(L
c
), corresponding to the union
of the ready events of each link in L
c
. Formally,
a system Σ is a triple
Σ = (C, L, G),
where C is the set of components, L the set of
links, and G the global priority hierarchy. The
latter is a DAG similar to the priority hierarchy P
of a component model, where the involved events
are pertinent to the whole system rather than to
DYNAMIC DIAGNOSIS OF ACTIVE SYSTEMS WITH FRAGMENTED OBSERVATIONS
251

single components. In other words, G enriches
the DAG obtained by the union of the single P’s
with additional precedence relationships among
the whole set of events in Σ.
Example 1 Displayed in Fig. 2 are the models
Breaker (top) and Protection (bottom), relevant
to the protection system outlined in Fig. 1. Each
model is depicted by the set of terminals (shaded
box) and the communicating automaton (graph).
Each input terminal is depicted as a triangle,
while each output terminal O is represented as a
bullet. The automaton relevant to the breaker in-
corporates two states, marked by 0 (closed) and 1
(open), respectively, and five transitions, namely
T
1
· · · T
5
, represented as arrows between states.
When the breaker is closed (state 0), either tran-
sition T
1
or T
3
is nondeterministically triggered
by event op on input terminal I. T
1
moves the
breaker to state 1 (closed) without generating
any output event. T
3
, instead, keeps the state of
the breaker unchanged (open), whilst generating
event f at output terminal O. Intuitively, this is
an abnormal transition (T
3
is depicted as a dotted
arrow), as the breaker is supposed to open when
triggered, which is not the case for T
3
. Event cl
is meant to close the breaker. When in state 1
(open), such an event triggers either T
2
(normal
behavior) or T
4
(faulty behavior). Note how the
same event triggers transition T
5
in state 0, leav-
ing the state unchanged (the breaker was closed
already). No priority relationships are assumed
for the breaker (P is empty).
The model of the protection embodies four in-
put terminals, I
1
· · · I
4
, and four output termi-
nals, O
1
· · · O
4
. Terminals O
1
and I
1
are meant
for connection with the breaker on the left of the
line, while terminals O
2
and I
2
are for the com-
munication with the breaker on the right (see
Fig. 1). Instead I
3
and O
3
allow the protection
to exchange events with the neighboring protec-
tion on the left. The same applies to I
4
and O
4
,
which are a means to communicate with the adja-
cent protection on the right. The corresponding
automaton involves four states, marked by 0 · · · 3,
and ten transitions, T
1
· · · T
10
. State 0 stands for
normal condition. The occurrence of a short cir-
cuit on the protected line is signaled by event sh
from the standard input In, which triggers tran-
sition T
1
. Such a transition moves the protection
to state 1 by generating event op at both output
terminals O
1
and O
2
, thus commanding the two
breakers to open. In state 1, the protection may
receive event f either at terminal I
1
or I
2
, mean-
ing that the relevant breaker failed to open. This
triggers either transition T
5
or T
6
, respectively,
each of which generates the recovery event rc at
output terminals O
3
and O
4
, respectively. The
Figure 2: Component models.
extinction of the short circuit is signaled by event
ok at the standard input terminal In, which trig-
gers transition T
2
that moves the protection to
state 0, while generating output events cl and ok
at terminals O
1
and O
2
, and O
3
and O
4
, respec-
tively. When a protection receives a request of re-
covery from a neighboring protection, it follows a
transition from state 0 to either 2 or 3, depending
on whether the request comes from the left (T
3
) or
from the right (T
4
), respectively. So, input event
(rc, I
3
) makes T
3
to generate (op, O
2
), that is, a
command to the breaker on the right. In state
2, since even this breaker may in turn be faulty,
the occurrence of event (f, I
2
) triggers transition
T
9
that, similarly to T
6
, propagates the recovery
request to the right-hand side protection. When
event ok is received at terminal I
3
from the neigh-
boring protection, transition T
7
moves the pro-
tection to state 0, while generating cl and ok at
terminals O
2
and O
4
, respectively. A symmetric
behavior is defined in state 3. We assume for the
protection a priority hierarchy such that (f, I
1
)
precedes both (ok, I
4
) and (ok, In), while both
(rc, I
3
) and (rc, In) precede (sh, In).
Depicted on the bottom of Fig. 3 is the topol-
ogy of a system Ψ that integrates the three com-
ponents protecting a generic line, namely protec-
tion p and breakers b
1
and b
2
. The protection is
connected with the breakers by means of links
L
1
· · · L
4
. We assume that all links share the
same model, where the event management M is
a simple queue. System Ψ is the abstraction of
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
252

a subpart of the protection system. Larger sub-
parts of the network may be assembled by con-
necting instances of Ψ together by means of links
among protections. The global priority hierar-
chy G of Ψ is such that (cl, I) of both break-
ers precedes (rc, I
3
), (sh, In), and (rc, I
4
), while
(op, I) of both breakers precedes (ok, I
3
), (ok, In),
(ok, I
4
), (f, I
1
), and (f, I
2
). ¤
3.1 Behavior Space
Given an initial state Σ
0
, system Σ evolves in
a way that is both consistent with its topology
and the behavioral models of its components and
links. The set of all possible evolutions can be
thought of as the behavioral model of Σ starting
at Σ
0
. The resulting graph is an automaton called
behavior space, Bhv (Σ, Σ
0
). A (possibly empty)
path between two nodes of the space is a history
segment of Σ. In particular, if the starting node
is the initial state of the space, then such a path
is a history of Σ
2
.
Example 2 Shown in Fig. 3 is the behavior
space relevant to system Ψ, where the initial state
is Ψ
0
= (S
0
, L
0
), where S
0
= (0, 0, 0) and L
0
in-
volves empty links. In each node, the record S
of the component states for b
1
, p, and b
2
is on
the top, while the record L of queues of events
within links L
1
· · · L
4
is on the bottom. Inciden-
tally, within the behavior space, at most one event
is stored in each link, so that the state of the
link can be expressed by either the label of the
event or a dash, the latter denoting the empty
link. Labels o and c are a shorthand for op and
cl, respectively. Nodes are marked by numbers
0 · · · 45. For instance, in node 7 both breakers
are closed (state 0 of the breaker model), while
the protection has commanded the breakers to
open (state 1 of the protection model). Besides,
links L
1
and L
4
are empty; instead, L
2
incorpo-
rates event f (meaning that b
1
has failed to open)
while L
3
contains event op, meaning that b
2
has
not yet reacted to the protection command. Each
edge is marked by a label identifying a component
transition. Specifically, single digits refer to tran-
sitions of the protection, while two-digit strings
correspond to breaker transitions. For example,
3, 31, and 42 stand for T
3
(p), T
3
(b
1
), and T
4
(b
2
),
respectively. Note how Ψ becomes reacting upon
the occurrence of an external event, either from
the standard input (triggering transition T
1
(p)) or
from a dangling terminal (triggering either T
3
(p)
or T
4
(p)).
2
The behavior space is introduced for formal rea-
sons, but never explicitly generated by the diagnostic
technique.
A history h(Ψ) is identified by the sequence
of labels (component transitions) marking the
edges on such a path, as for instance, h(Ψ) =
h1, 31, 12, 5i, corresponding to the following sce-
nario: (i) a short circuit occurs on the line pro-
tected by Ψ and protection p commands both
breakers b
1
and b
2
to open, (ii) breaker b
1
fails to
open, while (iii) breaker b
2
opens correctly, and
(iv) protection p asks the neighboring protection
on the left a recovery action. Finally, note the
cyclicity of Bhv(Ψ, Ψ
0
), which means that the set
of possible histories of Ψ is unbounded. ¤
4 DIAGNOSTIC PROBLEM
The ultimate task of diagnosis is the solution of
diagnostic problems. Within the domain of active
systems and the context of dynamic diagnosis, a
diagnostic problem concerns the operation of the
system and its solution is essentially based on the
model of the system and some clues on the sys-
tem reaction. Such a solution is a set of candidate
diagnoses, each diagnosis being a set of faults rel-
evant to a possible evolution of the system.
Formally, a fragmented diagnostic problem ℘
for a system Σ is a 4-tuple
℘(Σ) = (Σ
0
, V, O, R)
where Σ
0
is the initial state of Σ, that is, the state
of Σ when it starts operating, V is the viewer,
with specific visibility properties on the behav-
ior of Σ, O is the fragmented observation of Σ
gathered while Σ is operating, and R is the ruler,
which establishes what behavior of Σ is to be con-
sidered faulty and the granularity of the diagno-
sis.
4.1 Viewer
A viewer establishes what component transitions
are somewhat visible, as well as the specific ob-
servable label for each of them. Let T be the set
of transitions relevant to components in Σ, and V
a set of labels including the null label ε. A viewer
V is a mapping from T to V. If (T, ε) ∈ V, then
T is a silent transition, otherwise T is visible.
Example 3 A viewer V
ψ
for Ψ can be defined by
the set of visible transitions
3
, specifically V
ψ
=
{(T
1
(p), sh), (T
3
(p), l), (T
4
(p), r), (T
1
(b
1
), o
1
),
(T
2
(b
1
), c
1
), (T
1
(b
2
), o
2
), (T
2
(b
2
), c
2
)}. ¤
3
In order to keep the examples within a reasonable
complexity and without loss of generality, we assume
the visibility of the short circuit by means of the sh
label. In real application domains this is of course an
over-assumption.
DYNAMIC DIAGNOSIS OF ACTIVE SYSTEMS WITH FRAGMENTED OBSERVATIONS
253

Figure 3: System Ψ (shaded) and behavior space Bhv (Ψ, Ψ
0
).
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
254
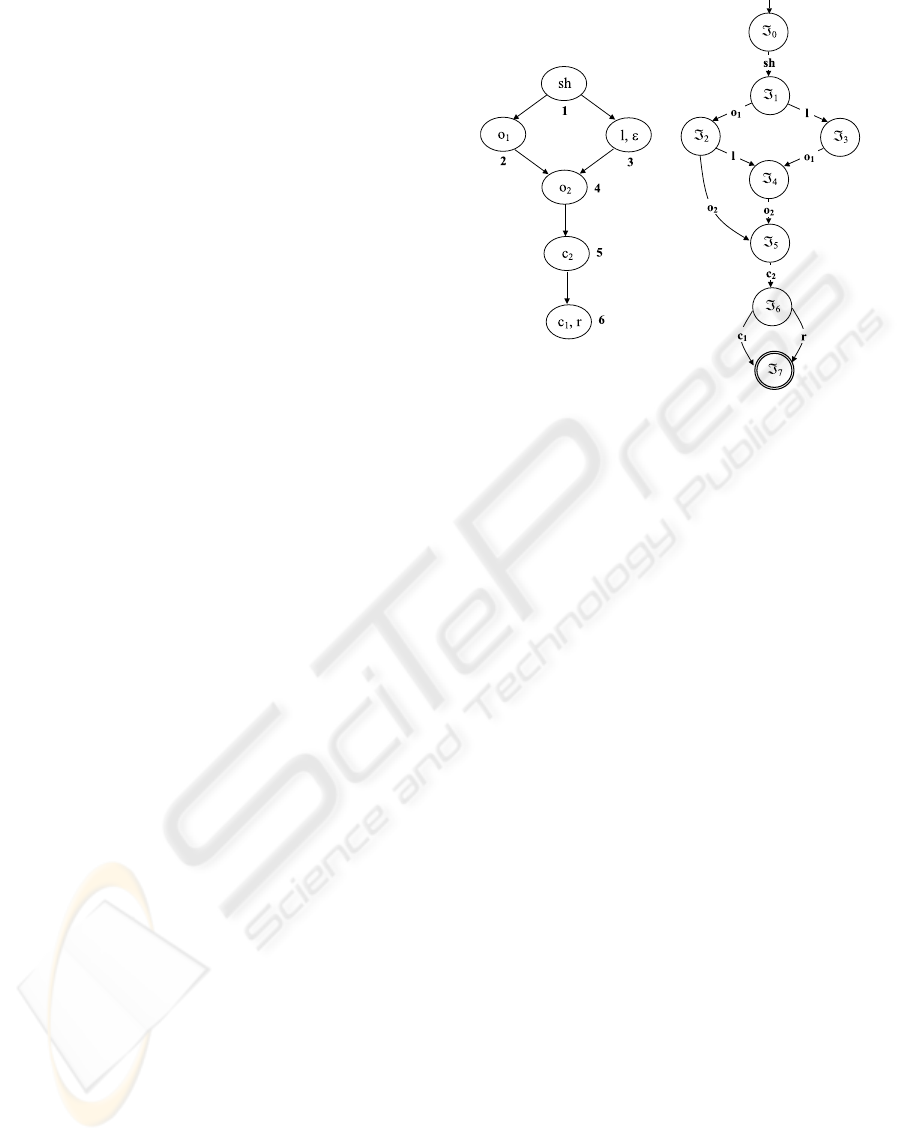
4.2 Fragmented Observation
When the system is operating, each visible tran-
sition is perceived by a viewer as a message. Each
message µ is a pair (λ, τ), where λ = {`
1
, . . . , `
k
}
is a set of labels in V, namely the logical con-
tent, while τ = {µ
0
1
, . . . , µ
0
h
} is a set of messages,
namely the temporal content, identifying all the
messages temporally preceding the current one.
A fragmented observation O is a list of mes-
sages,
O = hµ
1
, . . . , µ
n
i,
where a monotonicity assumption is assumed:
∀i ∈ [1 .. n], µ
i
= (λ
i
, τ
i
) (τ
i
⊆ {µ
1
, . . . , µ
i−1
}).
That is, the temporal content of a message µ is
supposed to refer to a (possibly empty) subset of
the messages preceding µ in O. Thus, a message
is uncertain in nature, both logically and tempo-
rally. Logical uncertainty means that λ includes
the actual (possibly null) label associated with
the transition in V that generated it, but further
spurious labels may be involved too. Temporal
uncertainty means that only partial ordering is
known among messages.
A fragmented observation may be mapped to
an observation graph,
γ(O) = (Ω, Υ, Ω
0
, Ω
f
),
where Ω is the set of nodes isomorphic to the
messages in O, Υ is the set of edges isomorphic
to the temporal contents of messages, Ω
0
⊆ Ω is
the set of roots, and Ω
f
is the set of leaves.
A precedence relationship is defined between
nodes of γ(O), specifically, ω ≺ ω
0
means that
γ(O) includes a path from ω to ω
0
, while ω ¹ ω
0
means either ω ≺ ω
0
or ω = ω
0
.
The graph is supposed to be in canonical form,
that is, if ω 7→ ω
0
is an edge in Υ, then there does
not exist any ω
00
such that ω ≺ ω
00
≺ ω
0
.
A sub-observation O
[i]
of O, where i ∈ [0 .. n],
is the (possibly empty) prefix of O up to the i-th
message, namely
O
[i]
= hµ
1
, . . . , µ
i
i.
If the following conditions hold:
µ
1
= ({`
1
}, ∅), ∀i ∈ [2 .. n] (µ
i
= ({`
i
}, {µ
i−1
})) ,
then O is a plain observation, and is denoted by
a list h`
1
, . . . , `
n
i of plain messages.
Example 4 A fragmented observation relevant
to viewer V
ψ
is O
ψ
= hµ
1
, . . . , µ
6
i, where µ
1
=
({sh}, ∅), µ
2
= ({o
1
}, {µ
1
}), µ
3
= ({l, ε}, {µ
1
}),
µ
4
= ({o
2
}, {µ
2
, µ
3
}), µ
5
= ({c
2
}, {µ
4
}), and
µ
6
= ({c
1
, r}, {µ
5
}). The relevant observation
graph γ(O
ψ
) is depicted on the left of Fig. 4. ¤
Figure 4: Observation graph (left) and relevant index
space (right).
4.3 Index Space
Since it is neither trivial nor efficient to reason
about the observation graph as is, an additional
(acyclic) automaton is considered, called the in-
dex space of the observation,
I(O) = (S, E, T, S
0
, S
f
),
where S is the set of states, E = V − {ε} the set
of events, T the transition function, S
0
the initial
state, and S
f
the set of final states. The pecu-
liarity of an index space lies in that each path
from the root to a final node, called a temporal
sequence, represents a mode in which labels may
be chosen in the observation graph without vio-
lating the constraints imposed by temporal and
logical uncertainty. The whole set of such paths
is the extension of I(O), denoted kI(O)k. Note
how each path within the extension is in fact a
plain observation consistent with O.
Example 5 Shown on the right of Fig. 4 is the
index space I(O
ψ
). The only final state is =
7
.
kI(O
ψ
)k includes six plain observations. ¤
4.4 Ruler
A ruler establishes what transitions are faulty.
Let T be the set of transitions relevant to com-
ponents in Σ, and R a set of labels including the
null label ε. A ruler R is a mapping from T to
R. If (T, ε) ∈ R, then T is normal, otherwise T is
faulty. A history segment h of Σ is said to imply a
diagnosis δ, where δ is the set of faults associated
with the faulty transitions of h defined in R.
DYNAMIC DIAGNOSIS OF ACTIVE SYSTEMS WITH FRAGMENTED OBSERVATIONS
255

Example 6 A ruler R
ψ
for Ψ can be defined
by the set of faulty transitions, namely R
ψ
=
{(T
1
(p), s), (T
3
(b
1
), fo
1
), (T
4
(b
1
), fc
1
), (T
3
(b
2
), fo
2
),
(T
4
(b
2
, fc
2
)}. ¤
5 DYNAMIC DIAGNOSIS
During its operation, a system Σ is expected to
react to external events and to generate a collec-
tion of observable events that are received as a
fragmented observation. Based on a fragmented
problem ℘(Σ) = (Σ
0
, V, O, R), the goal of dy-
namic diagnosis is to compute the set of candi-
date diagnoses at the occurrence of each newly
generated message.
At the beginning, no message is available, that
is, the fragmented observation is empty, namely
O = hi. However, in a strict sense, a first set
of candidate diagnoses relevant to the empty ob-
servation should be provided, as Σ might have a
silent reaction involving faulty transitions. At the
occurrence of the first message µ
1
, the monitor-
ing is required to yield the set of candidate diag-
noses relevant to O
[1]
= hµ
1
i. More generally, if
hµ
1
, . . . , µ
k
i is the current sequence of messages,
the occurrence of a new message µ
k+1
causes the
computation of the candidate diagnoses relevant
to O
[k+1]
= hµ
1
, . . . , µ
k
, µ
k+1
i. Furthermore, for
each message µ, dynamic diagnosis is required to
compute the set of candidate diagnoses implied by
the occurrence of µ, disregarding the whole set of
candidate diagnoses relevant to the sequence of
messages generated before µ. Thus, at the occur-
rence of the i-th message in O, both such kinds
of candidate sets are to be provided.
5.1 Silent Closure
Ideally, in order to perform dynamic diagnosis, we
need to know the state reached by the system at
the occurrence of each message. However, even in
case the previous state is univocally known, the
current state is bound to be uncertain owing to
silent transitions and the uncertain nature of the
message. On the other hand, the set of possible
states at each newly generated message is con-
fined within a limited domain, this corresponding
to all the states reachable via silent transitions.
This domain is a sort of (silent) closure of the
current state, which encompasses the part of the
behavior space that is transparent to the viewer.
Formally, let σ
0
be a node of the behavior space
Bhv(Σ, Σ
0
). The silent closure
Scl(σ
0
) = (S, E, T, S
0
, S
out
)
is an automaton such that S
0
= (σ
0
, D
0
) is the
root, and each state S ∈ S is a pair (σ, D) where
σ is a state of Bhv(Σ, Σ
0
) and D is a set of di-
agnoses δ where σ
0
à σ is a history segment in
Bhv(Σ, Σ
0
) that implies δ, called the candidate
attribute. E is the set of transitions of Σ.
T : S × E 7→ S is the transition function such
that (σ, D)
T
−→ (σ
0
, D
0
) ∈ T if and only if T is a
silent transition of Σ and σ
T
−→ σ
0
is a transition
in Bhv (Σ, Σ
0
).
S
out
⊆ S is the leaving set, defined as follows.
S = (σ, D) ∈ S
out
if and only if there exists a
visible transition σ
T
−→ σ
0
in Bhv (Σ, Σ
0
).
Example 7 With reference to the behavior
space outlined in Fig. 3, the silent closure of state
5, Scl (5), is the subgraph involving states 5, 23,
and 30, with S
out
= {23, 30}, whose states are
left by visible transitions T
2
(b
2
) and T
4
(p), re-
spectively. ¤
5.2 Monitor
The monitor relevant to a system Σ, an initial
state Σ
0
, a viewer V, and a ruler R is a graph
Mtr(Σ, Σ
0
, V, R) = (N, L, E, N
0
),
where N is the set of nodes, L the set of labels,
E the set of edges, and N
0
the initial node. Each
node N ∈ N is an automaton
N = (S, E, T, S
0
, S
out
) = Scl (S
0
),
where S
0
∈ Bhv(Σ, Σ
0
). Let
S
out
=
[
N∈N
S
out
(N), S
0
=
[
N∈N
{S
0
(N)},
and V and R the domain of labels in V and R,
respectively. Each edge E ∈ E is marked by a
label in S
out
× (V − {ε}) × R × S
0
. An edge
N
(S,`,ϕ,S
0
)
−−−−−−→ N
0
,
where S = (σ, D) and S
0
= (σ
0
, D
0
) are internal
nodes of N and N
0
, respectively, is such that:
(1) S
0
= S
0
(N
0
), namely, S
0
is the root of N
0
;
(2) σ
T
−→ σ
0
is a transition in Bhv(Σ, Σ
0
);
(3) ` is the (visible) label associated with T in V;
(4) ϕ is the label (possibly ε) associated with T in
R.
The initial node N
0
is such that S
0
(N
0
) =
(Σ
0
, D
0
).
Let N be a node of Mtr(Σ, Σ
0
, V, R). The lo-
cal candidate set ∆
loc
(N) of N is the union of
the candidate attributes relevant to the internal
states of N .
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
256
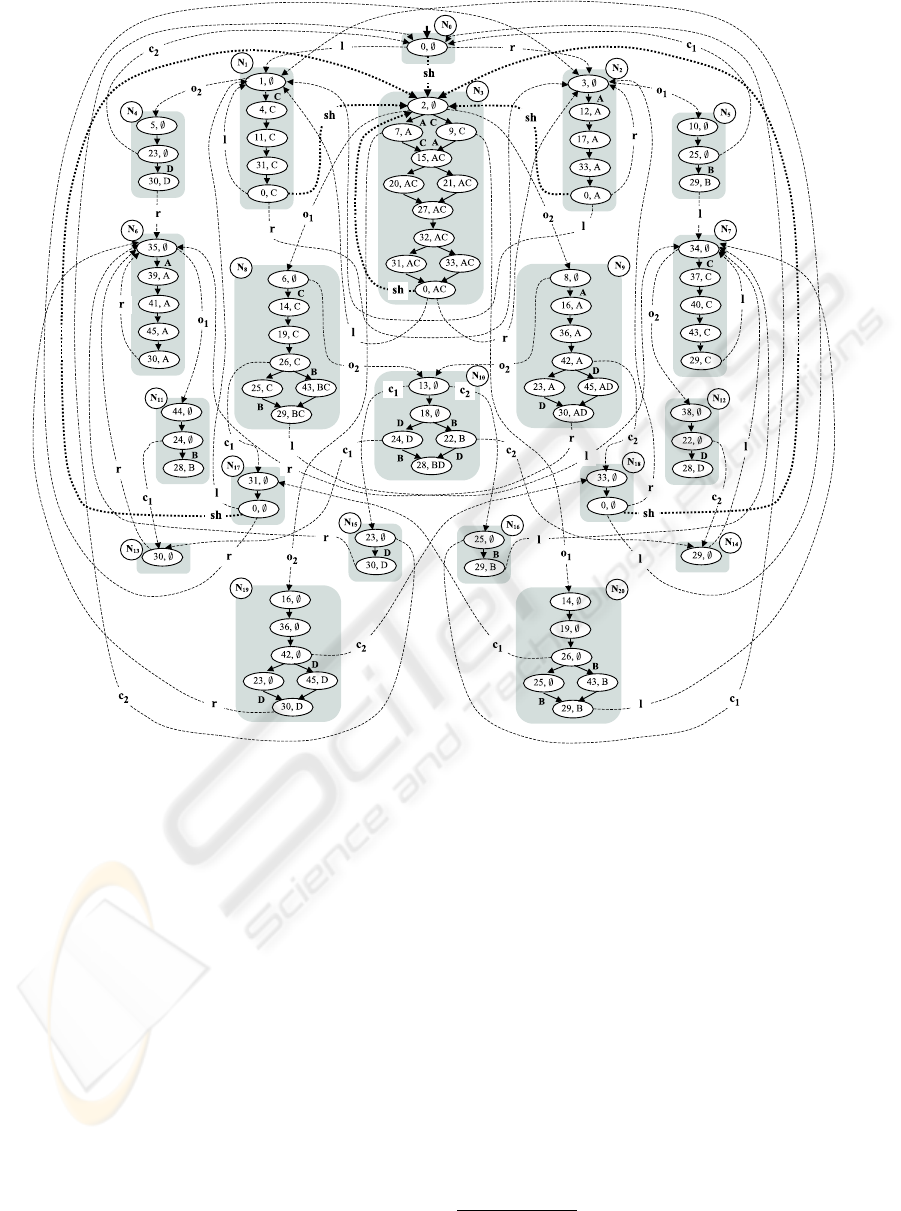
Figure 5: Monitor Mtr(Ψ, Ψ
0
, V
ψ
, R
ψ
).
Example 8 Portrayed in Fig. 5 is an
abstract representation of the monitor
Mtr(Ψ, Ψ
0
, V
ψ
, R
ψ
), where V
ψ
and R
ψ
are
defined in Examples 3 and 6, respectively. Each
node of the monitor is depicted within a shaded
box and labeled by an identifier N
i
, i ∈ [0 .. 20],
where N
0
is the root. Within each node, faulty
transitions are marked by letters A, B, C, or D,
which are a shorthand for faults fo
1
, fc
1
, fo
2
,
and fc
2
, respectively. Candidate attributes are
written as strings of such letters, e.g., AC is a
shorthand for {{A, C}} = {{fo
1
, fo
2
}}. Edges
between nodes are represented as arrows from
the internal state of the leaving node to the root
of the entering node, and marked by the relevant
viewer label. Identifiers of component transitions
are omitted (see Fig. 3). ¤
5.3 Monitoring Trajectory
The notion of a monitor allows us to trace the
state of the system based on a given fragmented
observation. However, such a state is uncertain
in nature for three reasons: (i) the uncertain na-
ture of the message, (ii) the unobservability of
the transitions within the nodes of the monitor,
and (iii) the nondeterministic nature of the mon-
itor, where different edges leaving the same node
can be marked by the same observable label
4
.
Let ℘(Σ) = (Σ
0
, V, O, R) be a fragmented di-
agnostic problem where O is a plain observation
h`
1
, . . . , `
n
i, and Mtr(Σ, Σ
0
, V, R) = (N, L, E, N
0
)
a relevant monitor. A context N is a triple
(N, S, H), where N is a node in N, S =
4
For instance, considering Fig. 5, there are two
different edges leaving node N
10
marked by label c
1
.
DYNAMIC DIAGNOSIS OF ACTIVE SYSTEMS WITH FRAGMENTED OBSERVATIONS
257

{δ
1
, . . . , δ
k
} is the snapshot context, where each
δ is either an empty set or a singleton incor-
porating the label of a faulty transition, and
H = {δ
0
1
, . . . , δ
0
k
0
} is the historic context, where
each δ
0
is a set of labels relevant to faulty transi-
tions.
The diagnostic join of two sets of diagnoses ∆
1
and ∆
2
is a set of diagnoses defined as follows:
∆
1
on ∆
2
= {δ | δ = δ
1
∪ δ
2
, δ
1
∈ ∆
1
, δ
2
∈ ∆
2
}.
A monitoring state M is a set {N
1
, . . . , N
m
}
of contexts. The monitoring trajectory of ℘(Σ),
Trj (℘(Σ)), is a sequence hM
0
, M
1
, . . . , M
n
i of
monitoring states (inductively) defined as follows:
(1) M
0
= {(N
0
, {∅}, {∅)}};
(2) For each i ∈ [1 .. n], M
i
is the minimal set
of contexts N
0
= (N
0
, S
0
, H
0
) such that N ∈
M
i−1
, N = (N, S, H), S ∈ S
out
(N), S =
(σ, D), N
(S,`
i
,ϕ,S
0
(N
0
))
−−−−−−−−−−→ N
0
∈ E, {ϕ} ∈ S
0
, and
H
0
⊇ (D on H on {{ϕ}})
5
.
Example 9 Considering Mtr(Ψ, Ψ
0
, V
ψ
, R
ψ
)
displayed in Fig. 5, assume the plain observation
O
0
ψ
= hsh, o
1
, li
and the corresponding diagnostic problem
℘
0
(Ψ) = (Ψ
0
, V
ψ
, O
0
ψ
, R
ψ
). The trajectory
Trj (℘
0
(Ψ)) will be hM
0
, M
1
, M
2
, M
3
i, where
M
0
= {(N
0
, {∅}, {∅})},
M
1
= {(N
3
, {{s}}, {{s}})},
M
2
= {(N
8
, {∅}, {{s}}), (N
20
, {∅}, {{s, C}})},
M
3
= {(N
7
, {∅}, {{s, B, C}})}. ¤
5.4 Candidate Sequence
Let ℘(Σ) be a problem involving a plain obser-
vation. A candidate pair
ˆ
∆ is an association
(∆
s
, ∆
h
) of two sets of diagnoses, where ∆
s
is the
snapshot candidate set, while ∆
h
is the historic
candidate set.
The candidate sequence
ˆ
∆(℘(Σ)) is a list
h
ˆ
∆
0
,
ˆ
∆
1
, . . . ,
ˆ
∆
n
i defined as follows.
ˆ
∆
0
is the
pair (∆
loc
(N
0
), ∆
loc
(N
0
)), where N
0
is the root
of Mtr (Σ, Σ
0
, V, R), while for each i ∈ [1 .. n],
ˆ
∆
i
= (∆
s
i
, ∆
h
i
), where:
∆
s
i
=
[
(N,S,H)∈M
i
(∆
loc
(N) on S)
∆
h
i
=
[
(N,S,H)∈M
i
(∆
loc
(N) on H)
where M
i
is the monitoring state correspond-
ing to the plain message `
i
in the trajectory
Trj (℘(Σ)).
5
By definition, if ϕ = ε then {ϕ} = ∅.
Example 10 With reference to the diagnostic
problem ℘
0
(Ψ) defined in Example 9, the candi-
date sequence
ˆ
∆(℘
0
(Ψ)) will be h
ˆ
∆
0
,
ˆ
∆
1
,
ˆ
∆
2
,
ˆ
∆
3
i,
where
ˆ
∆
0
= ({∅}, {∅}),
ˆ
∆
1
= ({{s}, {s, A}, {s, C}, {s, A, C}},
{{s}, {s, A}, {s, C}, {s, A, C}}),
ˆ
∆
2
= ({∅, {B}, {C}, {B, C}},
{{s}, {s, C}, {s, B, C}}),
ˆ
∆
3
= ({∅, {C}}, {{s, B, C}}).
Note how, at the arrival of the third message,
the historic candidate set reduces from the three
candidates of ∆
h
2
to the single diagnosis {s, B, C}
of ∆
h
3
. ¤
5.5 Index-Space Decoration
The notions of monitoring trajectory and can-
didate sequence have been introduced based on
plain observations. On the other hand, dynamic
diagnosis is meant for solving diagnostic prob-
lems with fragmented observations, where mes-
sages are both logically and temporally uncer-
tain. Such an observation is represented by a
DAG from which an index space can be gener-
ated, as shown in Section 4.3. Each state of the
index space corresponds to several possible ways
in which observable labels may have been gen-
erated by the evolution of Σ, that is, to several
plain observations. Thus, the computation of the
candidate sequence, in the general case, requires
associating each state = of the index space with
the set of monitoring states that are consistent
with all the plain observations relevant to =. In
other words, dynamic diagnosis requires an ex-
tension of the index space.
Let ℘(Σ) = (Σ
0
, V, O, R) be a fragmented di-
agnostic problem, and I(O) = (S, E, T, S
0
, S
f
) the
index space of O. The decoration of I(O) based
on ℘(Σ) is an automaton
I
∗
(O) = (S
∗
, E
∗
, T
∗
, S
∗
0
, S
∗
f
)
isomorphic to I(O), where each state S ∈ S is
marked by a monitoring attribute M as follows:
M =
[
O
0
∈kSk
M
k
where kSk denotes the set of plain observations
up to S in I(O), O
0
= h`
1
, . . . , `
k
i, ℘
0
(Σ) =
(Σ
0
, V, O
0
, R), Trj (℘
0
(Σ)) = hM
0
, M
1
, . . . , M
k
i.
Example 11 Consider the diagnostic problem
℘(Ψ) = (Ψ
0
, V
ψ
, O
ψ
, R
ψ
), where V
ψ
, O
ψ
, and
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
258

Table 1: Generation of the diagnostic sequence
ˆ
∆(℘(Ψ)).
i S
∗
f
i
∆
s
i
∆
h
i
0 {=
0
} {∅} {∅}
1
{=
1
} {{s}, {s, C}, {s, A, C}} {{s}, {s, C}, {s, A, C}}
2
{=
2
} {∅, {B}, {C}, {B, C}} {{s}, {s, C}, {s, B, C}}
3
{=
4
} {∅, {C}} {{s, B, C}}
4
{=
5
} {∅, {B}, {D}, {B, D}} {{s}, {s, B}, {s, D}, {s, B, C}, {s, B, D}, {s, B, C, D}}
5
{=
6
} {∅, {B}} {{s}, {s, B}, {s, B, C}}
6
{=
7
} {∅} {{s}}
R
ψ
are defined in Examples 3, 4, and 6, respec-
tively. Both the graph and the index space of O
are depicted in Fig. 4. The decoration of I(O) can
be expressed by determining each monitoring at-
tribute M
i
that is relevant to node =
i
, i ∈ [0 .. 7],
namely:
M
0
= {(N
0
, {∅}, {∅})},
M
1
= {(N
3
, {{s}}, {{s}})},
M
2
= {(N
8
, {∅}, {{s}}), (N
20
, {∅}, {{s, C}})},
M
3
= {(N
1
, {∅}, {{s, A, C}})},
M
4
= {(N
7
, {∅}, {{s, B, C}})},
M
5
= {(N
10
, {∅}, {{s}}), (N
12
, {∅}, {{s, B, C}})},
M
6
= {(N
16
, {∅}, {{s}}), (N
14
, {∅}, {{s, B}}),
(N
14
, {∅}, {{s, B, C}})},
M
7
= {(N
0
, {∅}, {{s}})}. ¤
Based on the concept of index-space decoration,
both notions of monitoring trajectory and can-
didate sequence can be straightforwardly gener-
alized to diagnostic problems involving a frag-
mented observation.
Let ℘(Σ) be a problem involving a fragmented
observation O = hµ
1
, . . . , µ
n
i. Let I
∗
(O
[i]
) =
(S
∗
i
, E
∗
i
, T
∗
i
, S
∗
0
i
, S
∗
f
i
) be the decorated index space
relevant to the sub-observation O
[i]
, i ∈ [0 .. n].
The trajectory of ℘(Σ) is the sequence of moni-
toring states hM
0
, M
1
, . . . , M
n
i, where
∀i ∈ [0 .. n]
M
i
=
[
(=,M)∈S
∗
f
i
M
.
The definition of the candidate sequence
ˆ
∆(℘(Σ))
does not change, as M
0
only depends on the root
of the monitor, while each pair
ˆ
∆
i
, i ∈ [1 .. n],
depends upon the monitoring state M
i
within the
trajectory.
Example 12 With reference to the diagnostic
problem ℘(Ψ) defined in Example 11, the candi-
date sequence
ˆ
∆(℘(Ψ)) will be h
ˆ
∆
0
,
ˆ
∆
1
, . . . ,
ˆ
∆
6
i,
as detailed in Table 1. Specifically, each sub-
observation O
[i]
is associated with the set of final
states S
∗
f
i
of the decoration =
∗
(O
[i]
), whose mon-
itoring attributes were computed in Example 11.
Note how the historic candidate set reduces to a
singleton {{s}} upon the arrival of the sixth mes-
sage. That is, a short circuit has occurred on the
protected line and the protection apparatus has
reacted correctly. ¤
Algorithm 1 The Diagnose procedure performs
dynamic diagnosis by generating the candidate
sequence relevant to a fragmented diagnostic
problem ℘(Σ) = (Σ
0
, V, O, R). Each diagnos-
tic pair within the sequence is generated at the
arrival of each message of O. Lines 1–3 create
the roots of the monitor and of the decorated in-
dex space based on the empty observation. The
core of the algorithm is the loop enclosed between
Lines 5–17. Each iteration of the loop is triggered
by the arrival of a new message (Line 6), which
causes the extension of the decorated index space
and of the monitoring space (Lines 7–9). At this
point, possible monitoring states correspond to
the monitoring attributes M of the current final
states of the decorated index space. Both snap-
shot and historic candidate sets are computed
based on the contexts incorporated in such at-
tributes M (Lines 12–13), so that the correspond-
ing candidate pair can be eventually generated
(Line 16).
procedure Diagnose(℘(Σ))
input
℘(Σ) = (Σ
0
, V, O, R): a fragmented problem;
side effects
Incremental generation of Mtr(Σ, Σ
0
, V, R),
Incremental generation of I
∗
(O ) = (S
∗
, E
∗
, T
∗
, S
∗
0
, S
∗
f
),
Generation of a candidate pair at each new message;
begin
1. Create the root N
0
of Mtr (Σ, Σ
0
, V, R);
2. Create the index space of the empty observation;
3. Mark the node of the index space with {(N
0
, {∅}, {∅)}};
4. Generate (∆
loc
(N
0
), ∆
loc
(N
0
));
5. loop
6. µ := the newly received message;
7. Extend the index space based on µ;
8. Extend the monitor based on Step 7;
9. Mark each new state of the index space
DYNAMIC DIAGNOSIS OF ACTIVE SYSTEMS WITH FRAGMENTED OBSERVATIONS
259

with the relevant monitoring attribute M;
10. for each (=, M) ∈ S
∗
f
do
11. for each (N, S, H) ∈ M do
12. ∆
s
:= ∆
s
∪ (∆
loc
(N) on S);
13. ∆
h
:= ∆
h
∪ (∆
loc
(N) on H)
14. end-for
15. end-for;
16. Generate (∆
s
, ∆
h
)
17. end-loop
end.
6 CONCLUSION
This paper has introduced a method for comput-
ing diagnoses during monitoring of a class of asyn-
chronous DESs that keep on being called active
systems although they have been endowed with
the new feature of a (local and global) priority hi-
erarchy. Also the notion of a diagnostic problem
has changed, having been introduced both a ruler
and a viewer in its definition. These new con-
cepts enable to decouple the (behavioral) models
of system components from the descriptions of
their observability and abnormality properties.
In the literature only a more limited separa-
tion between component models and observability
properties can be found: in (Console et al., 2002)
each specific problem assigns the same observabil-
ity to all the instances of the same component
type whereas each instance can be endowed with
distinct properties in the current approach. It is
worth noting that (Console et al., 2002) gives the
conceptual means to characterize model-based di-
agnosis, not to compute diagnoses, whereas our
proposal encompasses also operational methods.
As to the separation between component models
and abnormality properties, this belongs exclu-
sively to the approach described in the present
paper.
The essential novelty of the paper, however, is
the extension of dynamic diagnosis to fragmented
observations, these being uncertain observations
(Lamperti and Zanella, 2002) such that observ-
able events are received one by one and the re-
ception order does not reflect the emission order.
Each received message consists of a logical con-
tent and a (possibly) empty temporal content.
The logical content is uncertain in that it may
range over a set of labels, each of which may have
been emitted by several components. The avail-
able temporal content is uncertain since it does
not allow, in general, to determine one emission
order, instead, it is compliant with several ones.
A limiting monotonicity assumption implicit in
the notion of a fragmented observation is that the
temporal content of each newly received message
cannot place the emission of such a message after
that of any message that has not been received
yet.
The adopted algorithm for dynamic diagnosis
adapts that described in (Lamperti and Zanella,
2003a). However, in (Lamperti and Zanella,
2003a) it was assumed that the label inherent to
each received message was precisely identified and
the reception order exactly matched the emission
order. In the new algorithm, in order to handle
fragmented observations, the observation index
space is not computed beforehand as in (Lamperti
and Zanella, 2002), instead, it is built incremen-
tally, by updating it every time a new message
is received. This incremental construction, which
directly leads to a deterministic index space with-
out any need of generating a nondeterministic one
first, could indeed be proficiently exploited also
by a posteriori diagnosis.
The dynamic diagnosis algorithm is inherently
nonmonotonic since, as in (Lamperti and Zanella,
2003a), any estimate of the current system state
may not survive a new message. Orthogonally,
owing to temporal uncertainty in fragmented ob-
servations, every time a new message is received
further sequences of labels may have to be added
to the ones hypothesized so far. However, the
monotonicity assumption prevents any sequence
of labels hypothesized in previous monitoring
steps to be refuted. Future research will tackle
the relaxation of the monotonicity assumption,
thus introducing a second source of nonmono-
tonicity to be coped with by the reasoning mech-
anism. Another plan for future work is to apply
the modeling and reasoning principles described
in this paper to a real-world apparatus.
In the literature, monitoring-based diagnosis
of DESs is considered also by the diagnoser ap-
proach (Sampath et al., 1995; Sampath et al.,
1996) and the incremental decentralized diag-
noser approach (Pencol´e et al., 2001). Both con-
tributions differ from the current method in sev-
eral aspects. First, the class of considered systems
is different. In fact, while both the quoted ap-
proaches deal exclusively with synchronous DESs,
the new method can cope with asynchronous
ones, where every system may follow behavioral
silent cycles over time (which is not the case for
the diagnoser approach). Moreover, the exten-
sion of the current method to systems that in-
tegrate synchronous and asynchronous behavior
is straightforward (they are already dealt with in
(Lamperti and Zanella, 2003a), although consid-
ering certain plain observations only). Second,
both approaches consider an observation without
any uncertainty while the method introduced in
this paper takes as input a fragmented observa-
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
260

tion. Major differences inherent to the adopted
algorithms are highlighted and discussed in (Lam-
perti and Zanella, 2003a).
REFERENCES
Baroni, P., Lamperti, G., Pogliano, P., and Zanella,
M. (1999). Diagnosis of large active systems.
Artificial Intelligence, 110(1):135–183.
Console, L., Picardi, C., and Ribaudo, M. (2002).
Process algebras for systems diagnosis. Artifi-
cial Intelligence, 142(1):19–51.
Cordier, M. and Largou¨et, C. (2001). Using model-
checking techniques for diagnosing discrete-
event systems. In Twelfth International Work-
shop on Principles of Diagnosis – DX’01, pages
39–46, San Sicario, I.
Debouk, R., Lafortune, S., and Teneketzis, D. (2000).
A diagnostic protocol for discrete-event systems
with decentralized information. In Eleventh In-
ternational Workshop on Principles of Diagnosis
– DX’00, pages 41–48, Morelia, MX.
Fattah, Y. E. and Provan, G. (1997). Modeling tem-
poral behavior in the model-based diagnosis of
discrete-event systems (a preliminary note). In
Eighth International Workshop on Principles of
Diagnosis – DX’97, Mont St. Michel, F.
Lamperti, G. and Pogliano, P. (1997). Event-based
reasoning for short circuit diagnosis in power
transmission networks. In Fifteenth Interna-
tional Joint Conference on Artificial Intelligence
– IJCAI’97, pages 446–451, Nagoya, J.
Lamperti, G. and Zanella, M. (2002). Diagnosis of
discrete-event systems from uncertain tempo-
ral observations. Artificial Intelligence, 137(1–
2):91–163.
Lamperti, G. and Zanella, M. (2003a). Continuous di-
agnosis of discrete-event systems. In Fourteenth
International Workshop on Principles of Diag-
nosis – DX’03, pages 105–111, Washington DC.
Lamperti, G. and Zanella, M. (2003b). Diagnosis
of Active Systems – Principles and Techniques,
volume 741 of The Kluwer International Series
in Engineering and Computer Science. Kluwer
Academic Publisher, Dordrecht, NL.
Lunze, J. (2000). Diagnosis of quantized systems
based on a timed discrete-event model. IEEE
Transactions on Systems, Man, and Cybernetics
– Part A: Systems and Humans, 30(3):322–335.
Pencol´e, Y., Cordier, M., and Roz´e, L. (2001). Incre-
mental decentralized diagnosis approach for the
supervision of a telecommunication network. In
Twelfth International Workshop on Principles of
Diagnosis – DX’01, pages 151–158, San Sicario,
I.
Sampath, M., Sengupta, R., Lafortune, S., Sinnamo-
hideen, K., and Teneketzis, D. (1995). Diagnos-
ability of discrete-event systems. IEEE Trans-
actions on Automatic Control, 40(9):1555–1575.
Sampath, M., Sengupta, R., Lafortune, S., Sinnamo-
hideen, K., and Teneketzis, D. (1996). Fail-
ure diagnosis using discrete-event models. IEEE
Transactions on Control Systems Technology,
4(2):105–124.
DYNAMIC DIAGNOSIS OF ACTIVE SYSTEMS WITH FRAGMENTED OBSERVATIONS
261
