
AN EFFICIENT FRAMEWORK FOR ITERATIVE TIME-SERIES
TREND MINING
Ajumobi Udechukwu, Ken Barker, Reda Alhajj
ADSA Lab, Dept. of Computer Science, University of Calgary, AB, Canada
Keywords: Trend analysis, Time-series mining, Knowledge discovery and data mining
Abstract: Trend analysis has applications in several domains including: stock market predictions, environmental trend
analysis, sales analysis, etc. Temporal trend analysis is possible when the source data (either business or
scientific) is collected with time stamps, or with time-related ordering. These time stamps (or orderings) are
the core data points for time sequences, as they constitute time series or temporal data. Trends in these time
series, when properly analyzed, lead to an understanding of the general behavior of the series so it is
possible to more thoroughly understand dynamic behaviors found in data. This analysis provides a
foundation for discovering pattern associations within the time series through mining. Furthermore, this
foundation is necessary for the more insightful analysis that can only be achieved by comparing different
time series found in the source data. Previous works on mining temporal trends attempt to efficiently
discover patterns by optimizing discovery processes in a single run over the data. The algorithms generally
rely on user-specified time frames (or time windows) that guide the trend searches. Recent experience with
data mining clearly indicates that the process is inherently iterative, with no guarantees that the best results
are achieved in the first run. If the existing approaches are used for iterative analysis, the same heavy weight
process would be re-run on the data (with varying time windows) in the hope that new discoveries will be
made on subsequent iterations. Unfortunately, this heavy weight re-execution and processing of the data is
expensive. In this work we present a framework in which all the frequent trends in the time series are
computed in a single run (in linear time), thus eliminating expensive re-computations in subsequent
iterations. We also demonstrate that trend associations within the time series or with related time series can
be found.
1 INTRODUCTION
A time series X is an observed data sequence which
is ordered in time, X = x
t
, t = 1, …, n, where t is an
index of time stamps, and n represents the number of
data observations. Typical examples include stock
market data, weather data, and interaction flow data
(journey to work flows, telephone flows, etc.) A
time series is a sequence of real numbers, and may
be categorical or continuous. Categorical time series
have well defined segments, i.e., portions of the time
series can easily be classified as members of given
categories. For example, given a time series of
precipitation data and the minimum precipitation
that marks a drought. We can easily classify the time
series into periods of drought and periods of normal
precipitation. Translating categorical time series is
thus a trivial problem. However, for continuous time
series there are no well-defined categories. Several
approaches have appeared in the literature for
translating continuous time series: see e.g. (Agrawal
et al., 1995; Faloutsos et al., 1994; Keogh et al.,
2000; Perng et al., 2000; Qu et al., 1998; Yi and
Faloutsos, 2000). Most of the translation schemes
are developed to index and query similar time series.
We are interested in identifying all frequent trends
and trend associations that exist in any given time
series. Trends are qualitative movements that may
exist in a time series dataset. Figure 1 shows a
repeating trend in a time series. Frequently occurring
trends in time series are excellent pointers for
understanding the general behavior of the series.
130
Udechukwu A., Barker K. and Alhajj R. (2004).
AN EFFICIENT FRAMEWORK FOR ITERATIVE TIME-SERIES TREND MINING.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 130-137
DOI: 10.5220/0002620001300137
Copyright
c
SciTePress

Trends can also be a good start for mining
pattern associations existing within the time series,
or between a time series and other time series. For
example, a sales manager may be interested in
identifying periods when the sales pattern of a
product are similar, or when the sales pattern of a
given product is correlated to the sales patterns of
other products. A major objective of our work is to
achieve such trend discovery in a flexible framework
that allows efficient iterative analysis. Previous work
on time series translation, frequent pattern discovery,
and rule discovery requires domain and application
specific parameters from the users very early in the
process. Hence, the parameters guide (and prejudice)
the entire process. These approaches become
computationally very expensive if the user-specified
parameters and time windows are removed. Our
approach does not require time windows, and can be
applied to any domain. Furthermore, previous works
in the area only address the problem of finding
frequent patterns of a specified length while we lift
this restriction.
The rest of this paper is organized as follows.
Section 2 discusses related work. We discuss our
approach for encoding and finding frequent trends in
Sections 3 and 4. Section 5 discusses our technique
for identifying trend associations. We present the
analysis of our algorithms in Section 6. Our
experimental results are presented in Section 7, and
we conclude in Section 8.
2 RELATED WORK
Time series analysis and mining has received the
attention of several research groups. For example,
Indyk et al (Indyk et al., 2000) study the problem of
identifying representative trends in time series.
Given interval windows, their work aims at
identifying the interval that best approximates (or
represents) its neighbors. The problem they address
is, however, more related to identifying periodic
patterns in time series (Han et al., 1998). Qu et al
(Qu et al., 1998) present an approach for supporting
trend searches in time series data. Their work is in
the general area of time-series query processing and
assumes that the length of the query sequence is
known. The query sequence length is then used as a
window size for processing the time series data. A
match is found if the general trend of the best-fitting
line within a window is the same as that of the query
sequence. Adapting this approach in identifying all
frequent trends will require O(n
3
) time, thus, it is not
well suited for the problem we address in this paper.
Das et al. (Das et al., 1998) study the problem
of discovering rules in time series. Their approach
uses a sliding window of user-specified width to
extract subsequences from the time series. The
subsequences are then clustered into discrete groups
to complete the translation process. Rules may then
be obtained from the discretized series. Their
approach can be used to find trend associations by
normalizing the data in the subsequences, thus, is
related in spirit to the work presented in this paper.
However, their approach uses user-specified
windows, and would require a quadratic-time, all-
window approach to identify all frequent trends in
the time series. Furthermore, clustering the
subsequences requires the setting of parameters that
is guided by domain knowledge. If no parameters
are set, then, in the worst case, the number of
clusters may approach the number of subsequences
resulting in O(n
3
) time complexity for an all-window
approach. Other authors have studied rule discovery
in time series from the viewpoint of episodes (Harms
et al., 2001; Mannila et al., 1997). Episodes are
well-defined categories in time series, so they differ
from the problem addressed in this paper.
Patel et al. (Patel et al., 2002) address the
problem of identifying k motifs. A motif, as used in
their work, is a frequently occurring pattern in the
time series. The emphasis of their work is on real
data occurrences and not the movements or trends
existing between data entries. Their algorithm is
based on a user-specified sliding window
(representing the length of the patterns of interest),
and at best runs in sub-quadratic time. Adapting the
algorithm to identify all motifs of arbitrary lengths
will result in O(n
3
) time complexity, where n is the
size of the time series.
None of the previous works on temporal trend
discovery addresses the problem of finding all
frequent trends of arbitrary lengths. These works are
also guided by user-specified time windows that
dictate the lengths of the trends of interest. As a
Figure 1: An illustration of a repeating trend in time series.
AN EFFICIENT FRAMEWORK FOR ITERATIVE TIME-SERIES TREND MINING
131

result, these previous works generally require O(n
3
)
time to iteratively discover frequent trends of
arbitrary lengths. Our framework is developed to
support iterative analysis, and discovers all the
frequent trends in linear time.
3 TREND ENCODING
As a first step to time-series trend analysis, the time
series dataset has to be encoded in some way. As
discussed in Section 1, the encoding of categorical
time-series is trivial because the datasets have well
defined segments. Thus, the focus of our discussion
in this section is continuous time series data. The
data range for continuous time series is the set of
real numbers. Hence, as a first step to analyzing
continuous time-series, the data is discretized or
encoded by extracting relevant features from the
series. In our work, we require an encoding scheme
that adequately captures the movements or trends
existing in the time series. We also require an
encoding scheme that does not make use of time
windows so as to maintain efficient support for
iterative analysis. Most time series translation
schemes discussed in the literature require some
form of windows or domain-specific data
categorizations (Das et al., 1998; Faloutsos et al.,
1994; Keogh et al., 2000; Perng et al., 2000; Qu et
al., 1998; Yi and Faloutsos, 2000). Such encoding
schemes are inappropriate for our work.
The work by Agrawal et al. (Agrawal et al.,
1995) encodes the shapes in continuous time series
datasets. Each point in the series is translated based
on the relative change in the value of that point
compared to the previous point. The change can be
captured as a steep increase, increase, steep
decrease, decrease, no-change, or zero. We adapt
and generalize the shape-encoding concept
introduced in (Agrawal et al., 1995) for our work.
Our adapted scheme is discussed below.
3.1 Generalized Trend Encoding
The translation scheme used in this work is simple
and utilizes the relative changes in the time series
values to encode the series into a finite alphabet
string. We utilize a symmetrical alphabet encoding
that allows the matching of reverse patterns. The
underlying thought in our scheme is as follows:
given any two consecutive points on a continuous
time series, and knowing that the time series must be
changing in time; if the time component is
represented on one axis in a two dimensional plane,
then the line joining the two consecutive points must
be less than ninety degrees from the time axis in an
increasing or decreasing direction. Thus, we can
represent the relative movements in the time series
irrespective of the domain from which the data is
drawn. Figure 2 illustrates the overall concept.
The maximum value of angle ab is less than
90
0
, as is the maximum value of angle bc. The range
of angular values is maintained irrespective of the
data domain. Movements in the time series are then
simply encoded into alphabets based on the angles
between two neighboring data points. The alphabet
size can be greatly reduced or increased depending
on the level of detail desired. Using fewer alphabets
(i.e., angular categories) will result in approximate
matches.
To complete our discussion on the encoding
scheme, recall that the time component is assigned
to one of the axes. The time component, however, is
not on the same scale as the time series data entries.
The magnitude of the time component affects the
angle between the two data points. A natural choice
for the time unit is the recorded intervals at which
the data elements were collected. Alternatively,
given that the time series data elements were
collected at uniform intervals, and that the focus is
on discovering trends relative to the overall
movements in the series, we can establish a
distributive value for each time unit as follows:
TimeUnit = Change Space / Change Interval
Given a time series X = x
1
, x
2
, …, x
n
;
Change Space =
∑
=
−
−
n
i
ii
xx
2
1
||
, and
Change Interval = n – 1; where n is the size of the
time series. Given that x
i
and x
i+1
are two
consecutive entries in the series, and that θ is the
angle between them;
Tan θ =
T
imeUn
it
xx ii || 1 −+
The angle of change is then determined, and the
translation for that data point calculated accordingly.
The result is a string of length n-1 where n is the
number of data points in the original time series.
4 IDENTIFYING ALL FREQUENT
TRENDS
This Section presents the main contribution of this
paper, i.e., identifying all the frequent trends in the
time-series in one pass, thus, eliminating expensive
re-computations required by previous works to
achieve iterative analysis. We propose to identify all
frequent trends in any time series dataset by
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
132
representing the translated time series with a suffix
tree (Bieganski et al., 1994; Gusfield, 1997). Such a
representation would allow the identification of all
frequent trends in linear time. A suffix tree can be
used to represent a string composed from a finite
alphabet. A suffix tree for a string x of length n is a
rooted directed tree with exactly n leaves numbered
1 to n. The internal nodes of the tree, besides the
root node, must have at least two descendants. The
edges are labeled with nonempty sub-strings of x,
and no two edges originating from any particular
node can have edge-labels that start with the same
character. For any leaf i of the tree, the
concatenation of the edge-labels on the path from the
root to leaf i results in the suffix of string x from
position i.
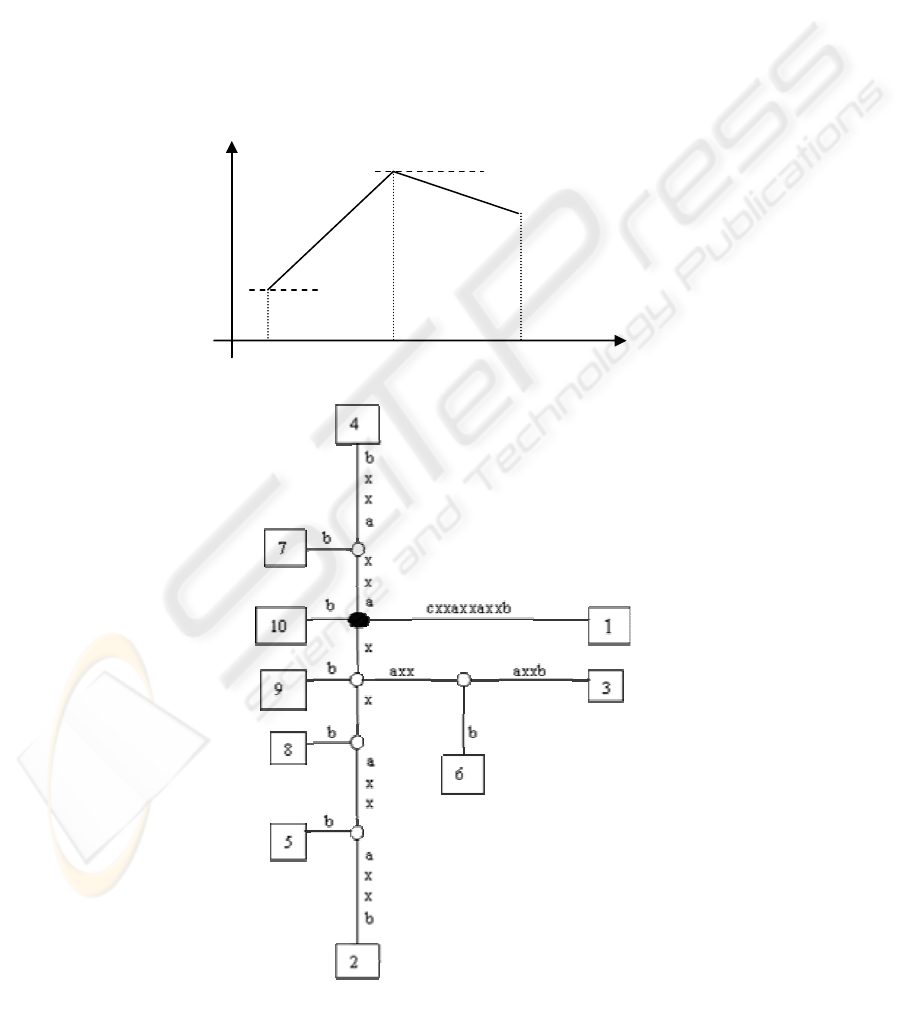
Figure 3 shows the suffix tree for string
“cxxaxxaxxb”. The following nomenclature is used
in the figure: the root node is depicted by a shaded
oval, the internal nodes by unshaded ovals; and the
leaf nodes by rectangles. Each leaf node is the path
taken by a particular suffix of the sequence, and is
named with the start position of that suffix. The label
of each node is the concatenation of all the edge-
labels for the path from the root to that node. The
suffix tree for “cxxaxxaxxb” has five internal nodes
with labels: “x”, “xx”, “xxaxx”, “axx”, and “xaxx”.
The labels of the internal nodes depict repeated parts
of the string. We wish to capture all the meaningful
repeated structures in the series without producing
overwhelming output, so we only select the
maximally repeated patterns that occur in maximal
pairs.
Figure 3: Suffix tree for string “cxxaxxaxxb”.
ab
x
z
bc
A
B
C
y
Time
Figure 2: Relative trends in time series.
AN EFFICIENT FRAMEWORK FOR ITERATIVE TIME-SERIES TREND MINING
133

Definition 1: Maximal pair: A maximal pair (or
maximally repeated pair) in a string s is a pair of
identical substrings r
1
and r
2
in s with the property
that the character to the immediate right (left) of r
1
is
different from the character to the immediate right
(left) of r
2
, thus, the equality of the two strings
would be destroyed if r
1
and r
2
are extended in either
direction.
Definition 2: Maximal repeat: A maximal repeat m
in string s is a substring of s that occurs in a maximal
pair in s.
Based on the definitions above, only 3 of the 5
node labels in Figure 3 are maximal repeats, these
are: “x”, “xx”, and “xxaxx”. The other repeated
patterns do not have independent occurrences that
are not within the maximal repeats. In our work, all
the patterns that participate in maximal repeats
(including their start and end points) are recorded in
a file using a simple format. The first element of
each record is a unique identifier we assign to each
pattern. The next element is the pattern, then the
number of occurrences of the pattern, and finally the
start and end points of all the occurrences. An
example of such a file is:
0; x; 6; 2,2; 3,3; 5,5; 6,6; 8,8; 9,9
1; xx; 3; 2,3; 5,6; 8,9
2; xxaxx; 2; 2,6; 5,9
Note that we enumerate all the occurrences of the
pattern, and not just its occurrences that are maximal
pairs. Thus, once a pattern has at least one
occurrence as a maximally repeated pattern, we
enumerate all its occurrences. The occurrences of a
pattern begin at all the leaf nodes that descend from
the node that has that pattern as the node label. Note
that both “x” and “xx” have higher occurrence
frequencies and they are sub-patterns of “xxaxx”.
The other repeated patterns always occur within
“xxaxx”, so they do not qualify as maximal patterns,
and can always be generated from “xxaxx”. Our
discussion so far is presented algorithmically below:
Input: Translated sequence (from time series)
Output: File containing maximal repeated
patterns
Steps:
1 Represent sequence with a suffix tree
2 Identify patterns with ≥ 1 maximally
repeated pair. For each pattern identified:
2.1 Assign a unique pattern-ID
2.2 Write the pattern, pattern-ID,
occurrence frequency, and start
and end positions of all its
occurrences to the output file
The steps discussed so far only need to be
carried out once on a given time series dataset. At
this stage, the user can retrieve all patterns of interest
by specifying the minimum frequency of occurrence,
or the minimum length of the pattern, or both. This
operation will require a simple query because we
have already stored all the maximal patterns and
frequencies in a file. This differs from existing
approaches that would require re-computation for
each new query specification.
The discussion so far has used a generalized
notion of repeating patterns. Special sets of repeating
patterns (such as non-overlapping repeats and
tandem repeats) may be derived from the general set
of frequent patterns by comparing the start and end
positions of the repeats.
5 MINING TREND
ASSOCIATIONS
Our algorithm for mining trend associations relies on
the set of maximal patterns found earlier. The
algorithm takes the file containing the set of
maximal patterns as input. The user has to set the
threshold (or minimum allowable) confidence for the
algorithm. For example, given that A and B are two
patterns discovered in the time series; assume
pattern A occurs four times, and that there are three
occurrences where B is found after A. The
confidence of the rule “B follows A” is ¾ (i.e., 75%).
There are also 3 optional user-specified inputs
to the algorithm. The first is the allowable time lag,
with a default of 0. For example, the user may want
the association “B follows A” to mean that B follows
A immediately, or the intent may be that B follows A
within at most 2 time units. The user may also
specify the minimum length of patterns considered
in the trend associations, and (or) the minimum
frequency of occurrence for a pattern to be
considered in the trend associations. These two
parameters aid in pruning the discovered rules to suit
the user’s specific interests. We use a subset of
Allen’s temporal interval logic (Allen, 1983;
Hoppner, 2001) to show the associations that may
exist between patterns in our framework. Figure 4
shows Allen’s interval relationships.
The first three relationships can be realized
between pairs of maximal patterns in our framework.
(The time-lag parameter only applies to the first rule
class.) However, the next three exist within maximal
patterns. For example, given that pattern A is
“xxaxx”, we can generate rules between the subparts
of A, such as “axx” finishes “xxaxx”. Rules like
these are rather obvious once we have the set of
maximal repeats.
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
134

The first three relationships in Figure 4 give
more interesting mining results. Notice that the
second relationship is equivalent to the first
relationship with zero time lag. To discover these
associations using our framework, we check the start
and end points of each pattern in the set of maximal
repeats against the start/end positions of all other
maximal patterns. For example, given two patterns
with unique id’s 0 and 1, and frequency counts 3 and
2, respectively; as shown below:
0; 3; 1,4; 8,11; 15,18
1; 2; 5,6; 12,13
Assuming a confidence threshold of 0.75, it is easy
to see that the rule “Pattern 0 occurs after Pattern 1
(i.e., every occurrence of pattern 0 follows an
occurrence of pattern 1)” cannot hold because there
are 3 occurrences of pattern 0 and only 2
occurrences of pattern 1, so at best, this rule would
have a 0.67 confidence.
On the other hand, the rule “Pattern 1 occurs
after Pattern 0 (i.e., every occurrence of pattern 1
follows an occurrence of pattern 0)” can be
discovered by comparing the start positions of
pattern 1 with the end positions of pattern 0. In
general, given that X.start represents the start point
of pattern X, and X.end represents the end point of
pattern X. Rules of the form “Pattern A occurs after
Pattern B (i.e., every occurrence of pattern A follows
an occurrence of pattern B)”, can be discovered by
finding the percentage of the occurrences of pattern
A that satisfy the inequality 0
≤ A.start – B.end ≤
time lag. This percentage must be up to the threshold
confidence for the rule to be returned (as true) to the
user. Similarly, rules of the form “Pattern A occurs
before Pattern B (i.e., every occurrence of pattern A
precedes an occurrence of pattern B)”, can be
discovered by finding the percentage of the
occurrences of pattern A that satisfy the inequality
0
≤ B.start – A.end ≤ time lag. The overlapping
relationship can be similarly defined.
Our framework can also be used to identify
associations between trends/patterns in multiple time
series. Each time series is encoded into a string, and
the maximal repeat patterns are extracted and stored
in a file using the techniques discussed earlier. The
rules are mined in the same way as those for a single
time-series, however, we can now define inequalities
to extract relationships in the form of the last four
Allen’s rules (see in Figure 4).
6 ANALYSIS
Our framework is composed of the following steps:
Step 1: Translation: Given that the time series has N
data elements, the translation takes O(N) time. The
result is a string of length N-1.
Step 2: Retrieving all frequent patterns: The suffix
tree is built in O(N) time. The disk-based approach
to suffix tree construction also runs in O(N) time.
Identifying the maximal repeats from the suffix tree
takes O(N) time. Thus, all the maximal frequent
patterns in our framework can be retrieved in linear
time.
Step 3: Mining trend associations: The time
required to discover the trend associations depends
on the number of maximal patterns, n. Each pattern
is compared with every other pattern in the file, thus
the operation runs in O(n
2
) time. In the worst case (if
the entire sequence is made up of the same
character), n = N-1. The number of participating
patterns may also be reduced by user-specified
parameters (such as minimum pattern-length and/or
time
A
B
A after B B before A
A is-met-by B B meets A
A is-overlapped-by B B overlaps A
A finishes B B is-finished-by A
A during B B contains A
A is-started-by B B starts A
A equals B B equals A
Figure 4: Allen’s interval relationships (Hoppner, 2001)
AN EFFICIENT FRAMEWORK FOR ITERATIVE TIME-SERIES TREND MINING
135

frequency). For practical applications, however, the
time series would be encoded with more than one
character, and patterns spanning multiple time
periods (e.g., ≥ 4) would be of greater interest, thus n
<< N.
7 EXPERIMENTAL EVALUATION
In our experiments we make use of several publicly
available datasets (Keogh, 2003; West, 2003). We
begin by translating each time series dataset. We
define 52 angular categories for encoding the
movements between pairs of entries in the time
series. Twenty-six of the categories are used for
increasing trends while the other twenty-six encode
decreasing trends. We use the average change space
to represent the time axis (see the discussion in
Section 3.1). The angular categories for increasing
movements are as follows: 0 – 39 degrees are
encoded with the letters a – h respectively, with 5-
degree increments between categories; 40 – 49
degrees are encoded with letters i – r respectively,
with 1-degree increments; 50 – 90 degrees are
encoded with letters s – z respectively, with 5-degree
increments. Decreasing trends are encoded in capital
letters using the same categories. We use more
discriminatory categories for angular changes
between 40 and 49 degrees. This is because the
mean movement has an angular change of 45
degrees when the time axis is represented by the
mean change space. Table 1 gives a summary of our
results on different datasets using 52 angular
categories. Reducing the number of categories used
can discover more approximate patterns. Table 2
shows the summary of our results when the angular
categories are reduced to 3. For both experiments,
time lag is set to 10 periods and threshold
confidence is 0.80. (Time-lag and confidence are
used for identifying trend associations. See the
discussion in Section 5). For the second experiment,
angular changes between –10 and +10 are taken as
no change (n), changes greater than 10 degrees are
encoded as increasing or decreasing trends (i or d)
respectively, depending on the direction of change.
Notice that for both experiments, the number of
frequent patterns is much smaller than the number of
entries in the time series. The number drops further
if the minimum pattern length is set ≥ 4. Notice also
that more frequent trends are reported in Table 2 for
each of the datasets. The trends are also longer and
generally occur more frequently. There are also
more trend associations. The increases are due to the
approximate matching achieved by using fewer
angular categories. The number of categories to use
should be guided by the analysis task at hand.
Generally, broader categories may be used to
identify broad segments of the time series with
similar movements. More discriminatory categories
however, should be used if identifying interesting
trend associations is the objective.
8 CONCLUSIONS
In this paper we have addressed the problem of
identifying all frequently occurring trends in time
series. We also show how to identify associations
existing in the discovered frequent trends. A major
underlying theme of the work presented in this paper
is the support for iterative trend discovery and
mining. The mining framework used in this paper is
well suited for both categorical and continuous time-
series datasets. Existing approaches for time series
trend discovery and mining require domain-specific
input very early in their processes, thus, the domain-
specific variables (such as time windows) drive the
subsequent stages of these algorithms. Our approach
does not make use of time windows, thus, all the
frequent trends existing in the dataset are identified
in the first pass. The identified trends are stored and
simply queried for subsequent analysis. Hence, our
approach is better suited for iterative trend analysis
because it does not require expensive re-computation
when parameters are changed during analysis.
Table 1: Summary of results with 52 angular categories
Dataset Length Number of
frequent
trends
Frequent trends
spanning at ≥ 4
time periods
Average freq. of
trends spanning
≥ 4 periods
Num. of trend
associations
Balloon 2001 768 412 5 31
Darwin 1400 421 1 2 5
Foetal_ecg 2500 694 22 2 10
Greatlakes 984 328 3 2 15
Industrial 564 190 1 2 17
Soiltemp 2304 772 90 2 20
Sunspot 2899 841 32 6 9
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
136

Table 2: Summary of results with 3 angular categories
Dataset Length Number of
frequent
trends
Frequent trends
spanning at ≥ 4
time periods
Average freq. of
trends spanning
≥ 4 periods
Num. of trend
associations
Balloon 2001 1200 1161 6 101
Darwin 1400 743 705 9 330
Foetal_ecg 2500 1510 1471 6 159
Greatlakes 984 510 471 8 221
Industrial 564 346 316 7 114
Soiltemp 2304 1404 1365 7 176
Sunspot 2899 1783 1744 7 159
REFERENCES
Agrawal, R., Psaila, G., Wimmers, E.L., and Zait, M.,
1995. Querying Shapes of Histories, Proceedings of
the 21
st
VLDB Conference, Zurich, Switzerland.
Allen, J.F., 1983. Maintaining Knowledge about Temporal
Intervals, Comm. ACM, 26(11):832-843.
Bieganski, P., Riedl, J., Carlis, J.V., and Retzel, E.R.,
1994. Generalized Suffix Trees for Biological
Sequence Data: Applications and Implementation, In
Proceedings of the 27
th
Hawaii Int’l Conference on
Systems Science, IEEE Computer Society Press, pages
35-44.
Das, G., Lin, K-I., Mannila, H., Ranganathan, G., and
Smyth, P., 1998. Rule Discovery from Time Series,
Proceedings of the 4
th
International Conference on
Knowledge Discovery and Data Mining, [KDD98],
New York, NY, pages 16-22.
Faloutsos, C., Ranganathan, M., and Manolopoulos, Y.,
1994. Fast Subsequence Matching in Time-Series
Databases, in Proceedings of the 1994 ACM SIGMOD
International Conference on Management of Data,
pages 419-429.
Gusfield, D., 1997. Algorithms on Strings, Trees, and
Sequences: Computer Science and Computational
Biology, Cambridge University Press.
Han, J., Gong, W., and Yin, Y., 1998. Mining Segment-
Wise Periodic Patterns in Time Series Databases,
KDD, pages 214-218.
Harms, S.K., Deogun, J., Saquer, J., and Tadesse, T.,
2001. Discovering Representative Episodal
Association Rules from Event Sequences Using
Frequent Closed Episode Sets and Event Constraints,
Proceedings of the IEEE International Conference on
Data Mining, Silicon Valley, CA, pages 603-606.
Hoppner, F., 2001. Discovery of Temporal Patterns,
Learning Rules about the Qualitative Behaviour of
Time Series, in De Raedt, L., Siebes, A., (Eds.),
PKDD 2001, LNAI 2168, Springer-Verlag, Berlin,
pages 192-203.
Indyk, P., Koudas, N., and Muthukrishnan, S., 2000.
Identifying Representative Trends in Massive Time
Series Data Sets Using Sketches, In Proceedings of the
26
th
Int’l Conference on Very Large Data Bases,
Cairo, Egypt, pages 363-372.
Keogh, E., 2003. The UCR Time Series Data Mining
Archive,
http://www.cs.ucr.edu/~eamonn/TSDMA/index.html
,
University of California – Computer Science and
Engineering Department, Riverside, CA.
Keogh, E.J., Chakrabarti, K., Pazzani, M.J., and Mehrotra,
S., 2000. Dimensionality Reduction for Fast Similarity
Search in Large Time Series Databases, Journal of
Knowledge and Information Systems, vol 3, number 3,
pages 263-286.
Mannila, H., Toivonen, H., and Verkamo, A.I., 1997.
Discovery of Frequent Episodes in Event Sequences,
Report C-1997-15, Department of Computer Science,
University of Helsinki, Finland.
Patel, P., Keogh, E., Lin, J., and Lonardi, S., 2002. Mining
Motifs in Massive Time Series Databases, Proceedings
of the IEEE Int’l Conference on Data Mining,
Maebashi City, Japan.
Perng, C-S., Wang, H., Zhang, S.R., and Parker, D.S.,
2000. Landmarks: A New Model for Similarity-,
Based Pattern Querying in Time Series Databases,
Proceedings of the 16
th
IEEE International Conference
on Data Engineering.
Qu, Y., Wang, C., Wang, X.S., 1998. Supporting Fast
Search in Time Series for Movement Patterns in
Multiple Scales, Proceedings of the ACM 7
th
International Conference on Information Management,
pages 251-258.
West, M., 2003. Some Time Series Data Sets, retrieved
June 18, 2003, from
http://www.stat.duke.edu/~mw/ts_data_sets.html
,
Duke University.
Yi, B-K, Faloutsos, C., 2000. Fast Time Sequence
Indexing for Arbitrary L
p
norms, in The VLDB
Journal, pages 385-394.
AN EFFICIENT FRAMEWORK FOR ITERATIVE TIME-SERIES TREND MINING
137
