
HIERARCHICAL MODEL-BASED CLUSTERING FOR
RELATIONAL DATA
Jianzhong Chen, Mary Shapcott, Sally McClean, Kenny Adamson
School of Computing and Mathematics, Faculty of Engineering, University of Ulster
Shore Road, Newtownabbey, Co. Antrim, BT37 0QB, Northern Ireland, UK
Keywords:
Hierarchical model-based clustering, relational data, frequency aggregates, EM algorithm.
Abstract:
Relational data mining deals with datasets containing multiple types of objects and relationships that are pre-
sented in relational formats, e.g. relational databases that have multiple tables. This paper proposes a proposi-
tional hierarchical model-based method for clustering relational data. We first define an object-relational star
schema to model composite objects, and present a method of flattening composite objects into aggregate ob-
jects by introducing a new type of aggregates – frequency aggregate, which can be used to record not only the
observed values but also the distribution of the values of an attribute. A hierarchical agglomerative clustering
algorithm with log-likelihood distance is then applied to cluster the aggregated data tentatively. After stopping
at a coarse estimate of the number of clusters, a mixture model-based method with the EM algorithm is devel-
oped to perform a further relocation clustering, in which Bayes Information Criterion is used to determine the
optimal number of clusters. Finally we evaluate our approach on a real-world dataset.
1 INTRODUCTION
Clustering aims at determining the intrinsic structure
of clustered data when no information other than the
observed values is available. Three types of clustering
methods have been widely used – hierarchical clus-
tering (Meil
˘
a and Heckerman, 1998), partition-based
clustering and model-based approach using mixture
models (Fraley and Raftery, 1998).
Most traditional clustering methods handle datasets
that have single relation in flat formats. Recently,
there has been a growing interest in relational data
mining (RDM) (D
ˇ
zeroski and Raedt, 2003; D
ˇ
zeroski
and Lavra
ˇ
c, 2001), which is tackling the problem of
mining relational datasets that contain multiple types
of objects and richer relationships and are presented
in relational formats that have more than one ta-
ble. RDM provides techniques for discovering use-
ful or unknown patterns and dependencies embed-
ded in relational databases. A common solution to
RDM is developing propositional methods that in-
tegrate traditional data mining techniques into rela-
tional data by converting or “flattening” multiple ta-
bles into a single table on which standard algorithms
can be run. One of the shortcomings of this approach
is that it may cause loss of meaning or information.
Another solution leads to relational approaches that
are capable of dealing with data stored in multiple
tables directly in the areas of inductive logic pro-
gramming (ILP) (D
ˇ
zeroski and Raedt, 2003; D
ˇ
zeroski
and Lavra
ˇ
c, 2001) and probabilistic relational models
(PRMs) (Friedman et al., 1999). Some initial work of
relational data classification and clustering based on
ILP and PRMs have been developed in (D
ˇ
zeroski and
Raedt, 2003; D
ˇ
zeroski and Lavra
ˇ
c, 2001; Emde and
Wettschereck, 1996; Taskar et al., 2001).
In this paper, we present a propositional method
which integrates traditional hierarchical model-based
clustering algorithms with relational data that is com-
posed of a set of composite objects. We use aggrega-
tion to efficiently flatten composite objects into flat
aggregate objects, to which model-based hierarchi-
cal agglomerative clustering with log-likelihood dis-
tance and the EM algorithm are then applied. In order
to discover rich aggregate knowledge from relational
data, we define frequency aggregates for composite
objects, which have vector data type and can be used
to record not only the observed values but also the dis-
tribution of the values of an attribute. Frequency ag-
gregates provide extended semantics in reducing the
information loss during aggregation and are helpful to
the computation of log-likelihood distance.
92
Chen J., Shapcott M., McClean S. and Adamson K. (2004).
HIERARCHICAL MODEL-BASED CLUSTERING FOR RELATIONAL DATA.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 92-97
DOI: 10.5220/0002624300920097
Copyright
c
SciTePress

2 OBJECT-RELATIONAL STAR
SCHEMA
Multi-relational data mining focuses on composite
objects. A general characterization defines a compos-
ite object consisting of several components (possibly
from different types) with relationships in between.
We assume the relationship between a composite ob-
ject and its components is aggregation and the objects
are stored in multiple database tables. A composite
object is defined as composed of a base (sub-object)
associated with a set of additional parts (sub-objects).
Two types of composite objects are distinguished cor-
responding with the two kinds of aggregation defined
in object-oriented modelling – shared aggregation,
where the parts may be parts in any wholes, and com-
position aggregation, in which the particular parts are
owned by one whole at a time and the existence of
the parts is strongly dependent on the existence of the
whole (Eriksson and Penker, 1998).
Two types of relational models can be used to
represent the two kinds of aggregation relationships
between the tables. One is relational star schema
(which can be generalized to the relational snowflake
schema), where the base table is in the middle and
the part tables radiate from the base
1
. A relational
star schema represents a shared aggregation in the
way that many-to-one relationships are specified from
base to parts. In comparison, a so called relational
aggregate schema, where in the middle is the base ta-
ble and the parts converge on the base, is defined to
represent a composition aggregation in the way that
many-to-one relationships are denoted from parts to
base. Figures 1 and 2 illustrate the schema graphs
and object diagrams of the two schemas respectively.
For example, it is natural to design a product sales
database using a relational star schema (Figure 1),
in which each sale is a composite object with a base
object of SaleRecord class (X
0
) and several sharable
part objects of classes ({X
k
}) such as Product, Time,
Geography, etc. An example of a relational aggre-
gate schema (Figure 2) used in the paper is to model
a housing condition survey database as composed of
a base table of Dwelling and two part tables of Occu-
pants and Rooms. In this way, each house is repre-
sented as a composite object that has a dwelling de-
scription record, a set of occupants who are living in
and a set of rooms of different living conditions.
The two schemas can be unified in the object-
relational (OR) context by introducing object iden-
tifiers (OIDs), reference (REF) and collection data
types (nested tables or collection of REF types) (Con-
nolly and Begg, 2002), which allow us to convert
1
The star schema is widely used in data warehousing
and OLAP, where the base table and part tables are called
the fact table and dimension tables respectively.
X
0
: base
X
1
: part
1
· · · · · ·
X
K
: part
K
X
1
: part
1
· · · · · ·
X
K
: part
K
1
m
1
m
∗
(a)
x
11
x
12
x
13
x
14
x
01
x
02
x
03
x
04
x
05
x
06
x
21
x
22
x
23
(b)
Figure 1: (a)The schema graph of relational star schema.
(b)An instance graph of relational star schema, including
6 composite objects, that contain 6 objects of base class X
0
,
4 objects of part class X
1
and 3 objects of part class X
2
.
X
0
: base
X
1
: part
1
· · · · · ·
X
K
: part
K
X
1
: part
1
· · · · · ·
X
K
: part
K
m
1
m
1
∗
∗
(a)
x
11
x
12
x
13
x
14
x
15
x
01
x
02
x
21
x
22
x
23
x
24
x
25
x
26
(b)
Figure 2: (a)The schema graph of relational aggregate
schema. (b)An instance graph of relational aggregate
schema, including 2 composite objects, that contain 2 ob-
jects of base class X
0
, 5 objects of part class X
1
and 6 ob-
jects of part class X
2
.
the many-to-one relationship in a relational aggregate
schema from parts-to-base into base-to-parts. In this
way, a relational aggregate schema can be replaced by
a star schema. We call the resulting schema as object-
relational star schema which is treated as a unified
representation of the relational star schema and rela-
tional aggregate schema. For the sake of simplicity,
we assume that only one composite class exists in the
dataset without recursive structures.
More formally, an object-relational star schema de-
fines a composite class X = {X
0
, X
1
, . . . , X
K
},
which consists of a base class X
0
and a set of
part classes {X
1
, . . . , X
K
}. Each class X
k
, 0 ≤
k ≤ K, is an abstract type of an entity in the
domain, and is associated with a set of attributes.
For a star schema, the base class is denoted as
X
0
(o, A
1
, . . . , A
M
0
, R
1
, . . . , R
K
) and the k-th part
class as X
k
(o, A
1
, . . . , A
M
k
). Three types of at-
tributes are distinguished. X
k
.o is used to specify an
unique system-generated object identifier for each ob-
ject of class X
k
. A descriptive attribute X
k
.A
m
, 1 ≤
m ≤ M
k
, represents an attribute of X
k
and takes
value from its domain Dom(X
k
.A
m
). A reference
attribute X
0
.R
k
, 1 ≤ k ≤ K, has domain of REF
HIERARCHICAL MODEL-BASED CLUSTERING FOR RELATIONAL DATA
93

type or collection type (e.g., a set of REFs). When
all the reference attributes are REF typed, an object-
relational star schema is identical with a relational
star schema; otherwise, we restrict it to stand for a
relational aggregate schema with composition aggre-
gation. In addition, an instantiation I of an object-
relational star schema X is composed of a set of N
composite objects, I
X
= {I
1
, I
2
, . . . , I
N
}, where
I
n
= {x
0
(n), x
n1
, . . . , x
nK
}, 1 ≤ n ≤ N; x
0
(n)
stands for the n-th object (or case) of the base class
X
0
in the database; x
nk
= {x
nk
(1), . . . , x
nk
(T
nk
)},
1 ≤ k ≤ K, T
nk
≥ 1, represents a subset of T
nk
objects of a part class X
k
involved in the n-th com-
posite object; x
nk
(t), 1 ≤ t ≤ T
nk
, is the t-th object
of class X
k
in the n-th composite object. Each ob-
ject is assigned an OID and a list of value mappings
from descriptive attributes to their domains and, for
the base class, an interpretation for all the reference
attributes. Moreover, in the n-th composite object, we
use x
0
(n).A
m
, x
nk
(t).A
m
and x
nk
.A
m
to denote the
observed value of attribute X
0
.A
m
in the base object,
the observed value of attribute X
k
.A
m
in any part ob-
ject, and the subset of observed values of attributes
X
k
.A
m
, respectively.
3 FREQUENCY AGGREGATES
In clustering, once the objects of analysis have been
determined, we are faced with the problem of finding
proper measures to decide how far, or how close the
data objects are from each other. The measures can
be either similarity or dissimilarity (Jain and Dubes,
1988). Dissimilarity, which is widely used in prac-
tice, can be measured in many ways and one of them
is distance. Distance measures depend on the type,
scale and domain of attributes we are analyzing. In or-
der to measure likelihood distance between compos-
ite objects, we present a “relational-to-propositional”
method of making composite objects comparable by
defining an aggregate object. The basic idea is to con-
vert each composite object into a single aggregate ob-
ject by preserving aggregate information of part ob-
jects. The notion of aggregate is borrowed from re-
lational algebra and set theory, where a multi-set of
values can be converted into a single aggregation or
summary value by applying with aggregate functions
or operations, such as COUNT, AVG in SQL and
MODE, MEDIAN in set theory.
More precisely, given a composite ob-
ject I
n
= {x
0
(n), x
n1
, . . . , x
nK
}, we de-
fine its aggregate object as AGG(I
n
) =
(AGG(x
0
(n)), AGG(x
n1
), . . . , AGG(x
nK
)),
where AGG(x
0
(n)) = (x
0
(n).o, x
0
(n).A
1
,
. . . , x
0
(n).A
M
0
); AGG(x
nk
) = (COUNT(x
nk
),
AGG(x
nk
.A
1
), . . . , AGG(x
nk
.A
M
k
));
COUNT(x
nk
) = |x
nk
| = T
nk
; if T
nk
= 1,
then AGG(x
nk
.A
m
) = x
nk
(1).A
m
, otherwise,
AGG(x
nk
.A
m
) is equal to a single value after
applying an aggregate function to the multi-set of
values x
nk
.A
m
.
The basic aggregate functions to achieve the pur-
pose could be any aggregate operations on a set: car-
dinality or count, maximum, minimum, mean or av-
erage, median, mode, sum, or even some compos-
ite aggregates, etc., depending on the type of at-
tributes. However, the general aggregators are only
good choices in some situations or under some condi-
tions, they are unable to represent the complete distri-
bution of values in a multi-set. We define a new type
of aggregate that is able to represent both value and
the distribution of values in a multi-set. A partial fre-
quency aggregate PFA(A, d) on a discrete attribute A
with Dom(A) = {v
1
, . . . , v
k
} in an observed multi-
set of objects d is defined to be a k-dimensional fre-
quency vector [f
d
1
. . . f
d
k
], where f
d
i
, 1 ≤ i ≤ k, is
the frequency of value v
i
within the set d. For ex-
ample, assume the attribute Gender has a domain
of {male,female}. The partial frequency aggregates
of two observations {2 males and 1 female} and {2
males and 3 females} are [
2
3
1
3
] and [
2
5
3
5
] respec-
tively. Together with the count number, PFA provides
a good description and statistics of a subset of part
objects, so that they are sufficient in calculating the
log-likelihood distances between (sets of) composite
objects. An example of a composite object and its ag-
gregate object is shown in Figure 3.
4 MODEL-BASED CLUSTERING
An integrated two-stage model-based clustering
method is developed based on the model-based clus-
tering strategy in (Fraley and Raftery, 1998), where a
mixture model is dealt with by applying HAC to pro-
vide tentative and suboptimal partitions, and the EM
algorithm to refine and relocate the partitions to reach
the optimal result.
4.1 Clustering Models
Here we assume a discrete multinomial mixture model
(Meil
˘
a and Heckerman, 1998) for a set of aggregate
attributes X = (AA
1
, . . . , AA
M
) and a set of aggre-
gate objects D = {x(1), . . . , x(N )}. Let Θ stand for
the set of parameters of the model, model-based HAC
is associated with a classification log-likelihood
`
C
(Θ, C; D) =
N
X
n=1
C
X
c=1
M
X
m=1
log P (x(n).AA
m
|θ
c
),
(1)
where c is used to label the classification: x(n) be-
longs to the c-th cluster only; and θ
c
represents the
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
94

Occupants (Age, Gender, Religion,
Income)
Dwelling (
Type, ConstructionDate, NetAssetValue, Location,
Tenure, Satisfaction,
{REF(Occupants)}, {REF(Rooms)})
Rooms (Function, Defect)
(o1, Adult, Male, Protestant, 20k-30k)
(o2, Adult, Female, Protestant, 10k-20k)
(o3, Child, Male, Protestant, None)
(o4, Child, Male, Protestant, None)
(o5, Old, Female, Catholic, None)
(d1, House, Post 1980, 61k-130k, Urban, Owner Occupied,
Yes, {o1,o2,o3,o4,o5}, {r1,r2,r3,r4,r5})
(r1, Kitchen, No)
(r2, LivingRoom, No)
(r3, Bedroom, No)
(r4, Bedroom, Yes)
(r5, Bathroom, No)
(OccupantsNo, AdultsNo, PfaGender, PfaReligion, TotalIncome) (RoomNo, BedroomNo, PfaDefect)
(5, 3, [0.6 0.4], [0.8 0.2 0], 30k+, d1, House, Post 1980, 61k-130k, Urban, Owner Occupied, Yes , 5, 2, [0.8 0.2])
Figure 3: An example of a composite object and aggregate object. Each attribute is set to be categorical. Three PFA attributes
are included.
set of parameters of the c-th model distribution, such
that Θ = {θ
1
, . . . , θ
C
}. In contrast, a mixture cluster-
ing model is used in the model-based clustering with
EM algorithm, and the relevant mixture log-likelihood
is expressed as
`
M
(Θ, C; D) =
N
X
n=1
log
£
C
X
c=1
π
c
M
Y
m=1
P (x(n).AA
m
|θ
c
)
¤
,
(2)
where π
c
is the mixing probability that an object be-
longs to the c-th cluster, π
c
≥ 0,
P
C
c=1
π
c
= 1; and
Θ = {θ
1
, . . . , θ
C
; π
1
, . . . , π
C
}.
Moreover, the likelihood ratio (LR) criterion
(Everitt, 1981) and Bayesian information criterion
(BIC) (Fraley and Raftery, 1998) are used to detect
the stopping rules and to determine the optimal num-
ber of clusters in the course of clustering. Let k be an
arbitrary number of clusters, q
m
be the number of cat-
egories of attribute AA
m
, r
m
be the number of vec-
tor values if AA
m
is a frequency aggregate attribute,
and M
v
be the total number of frequency aggregate
attributes; we then define, for a given data set D, the
log-likelihood ratio LR(D, k), the BIC score for mix-
ture classification model BIC
C
(D, k) and the BIC
score for mixture clustering model BIC
M
(D, k), re-
spectively, as
LR(D, k) = −2 log
`
C
(Θ, k; D)
`
C
(Θ, k + 1; D)
, (3)
BIC
C
(D, k) = −2`
C
(Θ, k; D) + δ
k
log (N), (4)
BIC
M
(D, k) = −2`
M
(Θ, k; D) + (δ
k
+ k − 1) log (N ), (5)
where δ
k
= k
£
P
M
m=1
(q
m
− 1) +
P
M
v
m=1
(r
m
− 1)
¤
.
Note that a frequency aggregate attribute has a do-
main of vector values with a dimension equal to the
number of categories of the original attribute it aggre-
gates from, so the total number of the independent
parameters of both two types of attributes (δ
k
) are
considered in the model complexity penalized term
of BIC scores. In addition, the number of mixing
probabilities (k − 1 for each object) must be penal-
ized in BIC for mixture models as well. The overall
hierarchical model-based clustering algorithm can be
expressed as follows.
1. Detecting stopping rules: Perform model-based HAC
for the data set D to reach up to 2 clusters, while com-
puting LR(D, c) and BIC
C
(D, c) for each cluster num-
ber c in each step; let C
l
= arg min(LR(D, c)) and
C
u
= d
C
l
+arg min(BI C
C
(D,c))
2
e be the lower bound and
upper bound of the stopping rules of further clustering.
2. Clustering: Perform the following two steps for each
number of clusters c = C
l
, . . . , C
u
2.1. Tentative clustering: Perform model-based HAC to
reach up to c clusters.
2.2. Relocation partitions: Perform the EM algorithm,
starting with c clusters from HAC and compute
BIC
M
(D, c).
3. Determining the optimal number of clusters: Choose
the clustering with the first local minimum of all the
BIC
M
(D, c) as the clustering result with the optimal
number of clusters, C = arg min(BIC
M
(D, c)).
4.2 Clustering Algorithms
The model-based HAC provides a likelihood distance
measure (Meil
˘
a and Heckerman, 1998), such that a
maximum log-likelihood (ML) can be maintained for
the joint probability density of all the data records.
For the discrete multinomial mixture model, the ML
of C
j
, the j-th cluster, takes the form
ˆ
l
j
(
ˆ
θ
j
; D
j
) =
M
X
m=1
q
m
X
q=1
N
jmq
log
N
jmq
N
j
, (6)
where
ˆ
θ
j
is the ML parameters of C
j
; D
j
is the set
of data cases involved in C
j
; N
j
and N
jmq
are the
number of cases (sufficient statistics) in C
j
and the
number of cases in C
j
whose m-th attribute takes the
q-th category of values, respectively. By merging two
clusters, e.g. C
j
and C
s
, and assigning all their data
cases to the newly formed cluster C
<j,s>
, the log-
likelihood distance d(j, s) is set to be the decrease in
ML resulting by the merge
d(j, s) =
ˆ
l
j
(
ˆ
θ
j
; D
j
)+
ˆ
l
s
(
ˆ
θ
s
; D
s
)−
ˆ
l
<j,s>
(
ˆ
θ
<j,s>
; D
<j,s>
).
The algorithm is described as follows, assuming we
maintain two linked lists of clusters and of aggregate
objects, and the stopping number of clusters is set to
be a pre-specified number K < N .
1. Initialization:
1.1. For n = 1, . . . , N , initialize C
n
to contain x(n);
HIERARCHICAL MODEL-BASED CLUSTERING FOR RELATIONAL DATA
95

1.2. For n = 1, . . . , N − 1, [for j = n + 1, . . . , N , com-
pute α
n
= min(d(n, j)) and β
n
= arg min
j
α
n
].
2. Iteration: For k = N, N − 1, . . . , K, do
2.1. get cluster with minimum distance: for i =
1, . . . , k, search C
n
with min(α
i
);
2.2. merge clusters: form C
<n,β
n
>
by merging C
n
and
C
β
n
, and set C
n
← C
<n,β
n
>
;
2.3. update clusters preceding C
n
: for n
0
= 1, . . . , n−1,
[compute d(n
0
, n) and update α
n
0
and β
n
0
if neces-
sary; if β
n
0
= β
n
then recompute α
n
0
and β
n
0
];
2.4. update the new formed cluster C
n
: for n
0
= n +
1, . . . , k, compute d(n, n
0
) and update α
n
and β
n
;
2.5. update clusters following C
n
: for n
0
= n +
1, . . . , β
n
− 1, if β
n
0
= β
n
then recompute α
n
0
, β
n
0
;
2.6. erase cluster C
β
n
from the cluster list.
3. Finish: For k = 1, . . . , K, output θ
k
, π
k
and C
k
.
The log-likelihood distance depends only on the ob-
jects of the clusters being merged, and all the other
distances remain unchanged. However, the time
complexity of the algorithm is between O(N
2
) and
O(N
3
) (Meil
˘
a and Heckerman, 1998).
Another issue is the computation of the distance be-
tween two clusters that contain each one object. For a
nominal (unordered) attribute, the Hamming distance
is used to calculate the differences between two ob-
served values; for an ordinal attribute, the normalized
Manhattan distance is applied; for a frequency aggre-
gate attribute that takes a vector value, the normalized
Euclidean distance between two vector values is cal-
culated with a normalized constant
1
√
2
.
In practice, HAC based on classification model of-
ten gives good, but suboptimal partitions. The EM
algorithm can further refine and relocate partitions
when started sufficiently close to the optimal value.
The mixture clustering likelihood is used as the basis
for the EM algorithm, because it models a conditional
probability τ
nk
that an object x(n) belongs to a clus-
ter C
k
, in contrast, τ
nk
is assumed to be either 1 or
0 in the classification model. The EM algorithm is
a general approach for maximizing likelihood in the
presence of hidden variables and missing data (Fraley
and Raftery, 1998), i.e. the class label attribute, τ
nk
and π
k
.
1. E-step: for n = 1, . . . , N and k = 1, . . . , K, compute
the conditional expectation of τ
nk
by
ˆτ
nk
=
ˆπ
k
P
k
(x(n)|
ˆ
θ
k
)
P (x(n))
=
ˆπ
k
Q
M
m=1
Q
q
m
q=1
ˆ
θ
x
mq
(n)
kmq
P
K
k=1
ˆπ
k
Q
M
m=1
Q
q
m
q=1
ˆ
θ
x
mq
(n)
kmq
where x
mq
(n) stands for the value (1 or 0) of x(n).AA
m
in its q-th category.
2. M-step: for k = 1, . . . , K, estimate the expectation of
π
k
and θ
k
by
ˆπ
k
=
1
N
N
X
n=1
ˆτ
nk
,
ˆ
θ
kmq
=
P
N
n=1
ˆτ
nk
x
mq
(n)
P
N
n=1
ˆτ
nk
.
The iteration will converge to a local maximum of the
likelihood under mild conditions, although the con-
vergence rate may be slow in most cases.
The BIC provides a kind of score functions that not
only measures the goodness of fit of the model to the
data, but also penalizes the model complexity, e.g. the
total number of model parameters or the storage space
of model structure. We apply BIC to both the classi-
fication model (Equation (4)) and the mixture cluster-
ing model (Equation (5)). Accordingly, the smaller
the value of BIC, the stronger the model. BIC
C
,
in model-based HAC, is used to compute the upper
bound (stopping rule) of the EM; and BIC
M
, in the
EM algorithm, is applied to find the optimal number
of clusters. A decisive first local minimum indicates
strong evidence for a model with optimal parameters
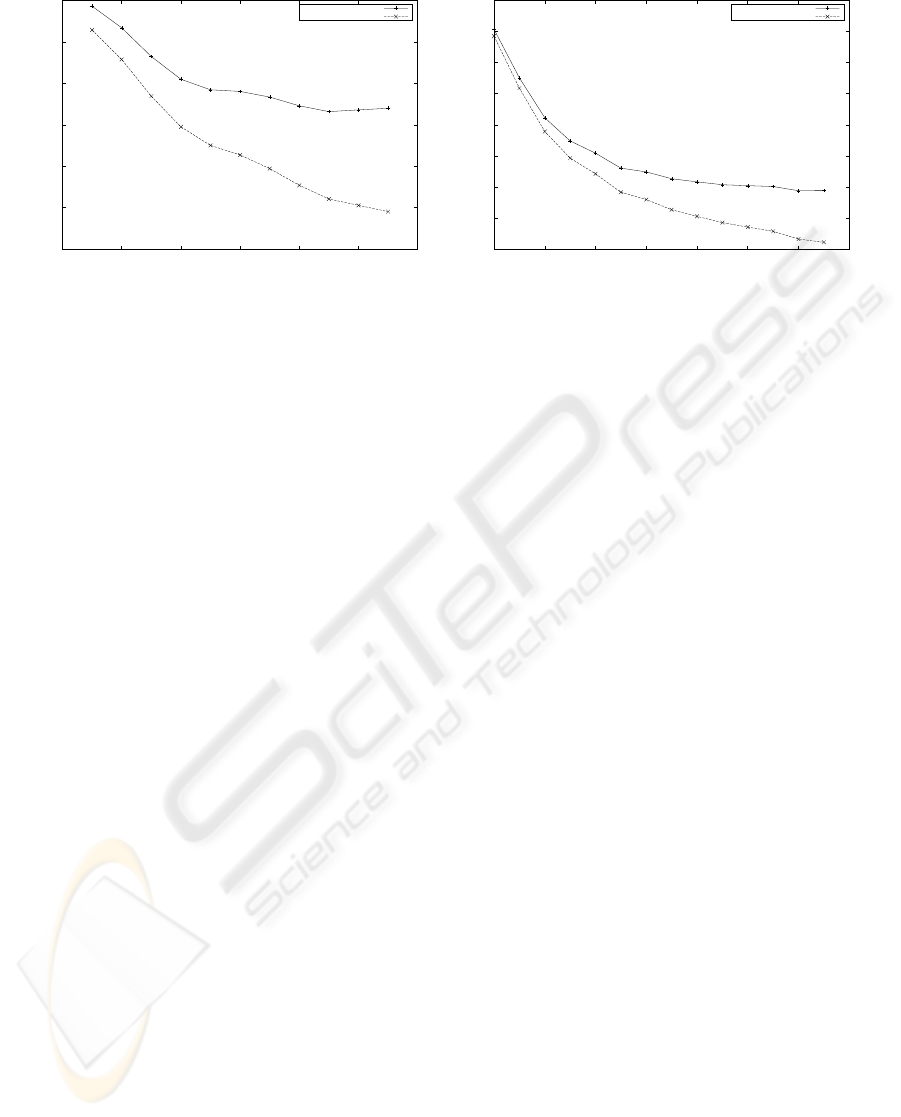
and number of clusters (see Figure 4 for example).
5 EXPERIMENTAL RESULTS
We apply the approach to a real world relational
dataset, which contains about 10,000 records of the
survey information of various types of dwellings. As
mentioned in section 2, the data is modelled using
a relational aggregate schema, where Dwelling table
plays a role of base class, with Occupants table and
Rooms table being two part classes. We chose some
significant attributes from the three tables and dealt
with their domains of values so that all the attributes
are categorical. After aggregating the attributes of
Occupants table and House table, we got a set of
composite objects with aggregate attributes of (Oc-
cupantsNo, AdultsNo, PfaGender, PfaReligion, Total-
Income, RoomNo, BedroomNo, PfaDefect), in which
PfaGender, PfaReligion and PfaDefect are three par-
tial frequency aggregate attributes with vector values
(see an example in Figure 3).
Table 1: Experimental Result
number of objects 1,000 3,000 5,000 9,530
(Lower,Upper) Bound (2,7) (2,11) (3,13) (2,15)
number of clusters 6 9 11 14
HAC running time (sec.) 50 427 1,159 4,024
After clearing the objects that have missing data,
we got 9,530 aggregate objects left, from which
four groups are selected for clustering, 1,000 objects,
3,000 objects, 5,000 objects and the whole dataset.
The EM algorithm runs until either the difference be-
tween successive log-likelihood is less than 10
−5
or
100 iterations are reached. The results for the four
groups is listed in Table 1. Figure 4 show the two
plots of the mixture BIC scores and −2log-likelihood
values against the number of clusters for the last two
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
96
170000
175000
180000
185000
190000
195000
200000
2 4 6 8 10 12 14
BIC score & -2log-likelihood
number of clusters
BIC score & log-likelihood versus the number of clusters for 5,000 composite objects
BIC score
-2log-likelihood
330000
340000
350000
360000
370000
380000
390000
400000
410000
2 4 6 8 10 12 14 16
BIC score & -2log-likelihood
number of clusters
BIC score & log-likelihood versus the number of clusters for 9,530 composite objects
BIC score
-2log-likelihood
Figure 4: The BIC and log-likelihood versus the number of clusters for the datasets of 5,000 and 9,530 composite objects. The
first local minimum shows the optimal numbers of clusters found by the EM algorithm are 11 and 14 clusters respectively.
groups respectively. An observation from the exper-
iments is that the optimal number of clusters found
by the algorithm is increasing as the total number of
objects increases. This can be verified from Equation
(5), where the likelihood term (O(N)) dominates the
penalty term (O(log N)) as N gets larger.
The clustering results are significant and convinc-
ing. The count aggregates and frequency aggregates
play important roles in the clustering. The dataset
tends to be partitioned into groups that have dis-
tinct number of part objects, e.g., dwellings with
distinct number of occupants and rooms, together
with properties of distinct aggregate frequencies, e.g.,
dwellings of protestant families and dwellings in
which fewer room defects are reported. In addition,
by analysing the BIC curves in Figure 4, it is reason-
able for us to partition the whole dataset into 7 distinct
clusters at last.
6 CONCLUSION
Compared with other work, our method is a proposi-
tional approach in relational data mining. We bor-
rowed some ideas from (Fraley and Raftery, 1998;
Meil
˘
a and Heckerman, 1998), and provide some ex-
tensions in dealing with aggregate attributes. We de-
fine frequency aggregates so that both the values and
the distribution of values can be recorded for compos-
ite objects. Frequency aggregates are well applied in
computing log-likelihood distance. We also present
a method of determining the lower and upper bounds
for the EM and get good results from the experiments.
Some future work are planned to do: handling con-
tinuous attributes as well as discrete attributes; deal-
ing with missing data or data with noise; and apply-
ing relational distance measurements, e.g. (Emde and
Wettschereck, 1996) to develop a relational model-
based clustering method.
REFERENCES
Connolly, T. M. and Begg, C. E. (2002). Database Systems:
A Practical Approach to Design, Implementation, and
Management. Harlow: Addison-Wesley, third edition.
International computer science series.
D
ˇ
zeroski, S. and Lavra
ˇ
c, N. (2001). Relational Data Min-
ing. Springe-Verlag, Berlin.
D
ˇ
zeroski, S. and Raedt, L. D. (2003). Multi-relational data
mining: a workshop report. SIGKDD Explorations,
4(2):122–124.
Emde, W. and Wettschereck, D. (1996). Relational
instance-based learning. In Proc. ICML-96, pages
122–130, San Mateo, CA. Morgan Kaufmann.
Eriksson, H.-E. and Penker, M. (1998). UML Toolkit. John
Wiley and Sons, New York.
Everitt, B. (1981). Cluster Analysis. Halsted Press: John
Wiley and Sons, New York, second edition.
Fraley, C. and Raftery, A. (1998). How many clusters?
which clustering method? answers via model-based
cluster analysis. The Computer Journal, 41(8):578–
588.
Friedman, N., Getoor, L., Koller, D., and Pfeffer, A.
(1999). Learning probabilistic relational models. In
Proc. IJCAI-99, pages 1300–1307, Stockholm, Swe-
den. Morgan Kaufmann.
Jain, A. K. and Dubes, R. C. (1988). Algorithms for Clus-
tering Data. Prentice-Hall.
Meil
˘
a, M. and Heckerman, D. (1998). An experimen-
tal comparison of several clustering and initialization
methods. In Proc. UAI 98, pages 386–395, San Fran-
cisco, CA. Morgan Kaufmann.
Taskar, B., Segal, E., and Koller, D. (2001). Probabilis-
tic classification and clustering in relational data. In
Nebel, B., editor, Proc. IJCAI-01, pages 870–878,
Seattle, US.
HIERARCHICAL MODEL-BASED CLUSTERING FOR RELATIONAL DATA
97
