BUILDING PROVEN CAUSAL MODEL BASES FOR STRATEGIC

DECISION SUPPORT

Christian Hillbrand

Liechtenstein University of Applied Sciences

urst-Franz-Josef-Strasse, LI-9490 Vaduz, Principality of Liechtenstein

Keywords:

Strategy planning, universal function approximation, causal proof, Artiﬁcial Neural Networks.

Abstract:

Since many Decision Support Systems (DSS) in the area of causal strategy planning methods incorporate

techniques to draw conclusions from an underlying model but fail to prove the implicitly assumed hypotheses

within the latter, this paper focuses on the improvement of the model base quality. Therefore, this approach

employs Artiﬁcial Neural Networks (ANNs) to infer the underlying causal functions from empirical time

series. As a prerequisite for this, an automated proof of causality for nomothetic cause-and-effect hypotheses

has to be developed.

1 INTRODUCTION

The main task of corporate strategy planning is the

construction of a variety of decisions which are highly

interrelated and characterized by a rather complex

informational background. In order to reduce this

complexity, the raw data originating from operational

databases or Management Information Systems has

to be arranged within decision models which be-

comes the principal issue of Decision Support Sys-

tems (DSS). Hence it can be observed that the archi-

tecture of any DSS necessarily incorporates the notion

of a mental model underlying the respective decision

theory as well as appropriate decision techniques.

A considerable number of recent approaches within

the domain of strategic decision making propose to

organize business indicators in the form of causal

models. The main task of these models is to visu-

alize the cause-and-effect hypotheses between given

variables (Hillbrand and Karagiannis, 2002). Well-

known examples for this type of strategic decision

methodologies are the Balanced Scorecard technique

(Kaplan and Norton, 2004), the tableau de board

methodology (Mendoza et al., 2002), as well as cy-

bernetic concepts like VESTER’s Biocybernetic Ap-

proach (Vester, 1988) or the St. Gallen Management

Model (Schwaninger, 2001).

Although these managerial approaches for strategic

decision support provide some practical aspects for

the reduction of complexity, the implementations of

these ideas in the form of DSS are rather weak (Hill-

brand and Karagiannis, 2002, p. 368): The model

base, however, usually remains unproven with respect

to the empirical evidence of the hypothetic cause-and-

effect relations. Moreover these techniques are not

able to provide quantitative forecasts for future im-

pacts of an analyzed strategic scenario.

The discussion in this area restricts to the concept

of correlation to prove causal relations. As this tech-

nique fails to sufﬁciently explain the phenomenon of

causality, the relevant literture predominantly shares a

rather dogmatic conception that it is not admissible at

all to assess relations of this type (Hillbrand, 2003a,

pp. 6ff.).

However, if we abandon the restriction to corre-

lation as a concept for the proof of causality and a

measure of association, it seems to be possible to in-

fer further causal knowledge from empirical data and

therefore improve the quality of the model base sig-

niﬁcantly. Hence this paper proposes an approach to

automatically prove managerial cause-and-effect rela-

tions and to approximate the unknown causal function

underlying these associations.

Based on a brief overview of causality concepts in

section 2 this paper proposes a methodology to prove

the causality of nomothetic cause-and-hypotheses in

section 3 as well as to approximate the underlying

functions (section 4) based on empirical evidence.

The paper is concluded by the presentation of experi-

mental results in section 5.

178

Hillbrand C. (2004).

BUILDING PROVEN CAUSAL MODEL BASES FOR STRATEGIC DECISION SUPPORT.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 178-183

DOI: 10.5220/0002625101780183

 SciTePress

2 CAUSALITY CONDITIONS

As it has been outlined in the introduction, the mere

correlation of two variables seems to be insufﬁcient

for the causal validation of associations between

them. Moreover, causality per se cannot be observed

or tested by objective means. According to KANT it

is a synthetic judgment a priori (Schnell et al., 1999,

p. 56). Causality must therefore be regarded as an as-

sumption about the connection between cause and ef-

fect made by the human mind and based on a variety

of experiences rather than some kind of natural phe-

nomenon which can be observed in an objective man-

ner. Therefore some notions of causality incorporate

the interventionistic idea which suggests the admis-

sibility of experimental results as the only proof for

causality. In an enterprise, however, there is hardly

any situation where an experiment-like situation can

be created because the trial-and-error manner of these

settings usually would inﬂict losses for the business

and the response time of basic cause-and-effect rela-

tions can be rather long.

Applied to managerial cause-and-effect relations,

an appropriate concept of causality must restrict itself

to observational studies in terms of empirical data as a

consequence. Therefore a ﬁrst necessary but not sufﬁ-

cient criterion (conditio sine qua non) for causality is

that a cause provides information which can be used

to (partly) explain its effects. In case of linear cause-

and-effect relations this property of informational re-

dundancy is also known as correlation or covariance.

However, as it has been shown in the introduction,

these concepts fail to fully explain causality. Accor-

ding to HUME, there has to be a temporal precedence

relation between a cause and its effects additionally to

informational redundancy. Regardless of the ability of

these two necessary properties to fully explain many

causal relations, there still remains the problem of an

exogenous common cause to induce spurious associa-

tions between presumably causal variables. Therefore

the deﬁnition of causality has to be enhanced by the

postulate to control for this type of association.

Based on an extensive research of causality con-

cepts within the relevant literature (Hillbrand, 2003a,

pp. 152 – 170) the following deﬁnition of an appro-

priate concept of causality to analyze associations be-

tween managerial variables can be derived:

Theorem 1 (managerial causal relation): A causal

relation between variables of a managerial system ex-

ists if and only if there exist appropriate nomothetic

(i.e. unproven) cause-and-effect hypotheses based on

causal a priori knowledge where the following condi-

tions are fulﬁlled:

• The empirical observations of a potential cause

provide informational redundancy regarding its po-

tential effect.

• The variation within the time series of the poten-

tial cause must always precede the response of this

variation within the time series of the potential ef-

fect.

• The three causality properties as deﬁned above

(causal a priori knowledge, informational redun-

dancy and temporal precedence) must not originate

from the inﬂuence of a known or unknown cause,

common to the potential cause and the potential ef-

fect. ¤

As it is obvious from the above theorem, the under-

lying notion of causality follows the ideas of logical

empirism which regards a hypothesis as true as long

as it cannot be falsiﬁed. Therefore it is the task of

a causality proof to rule out non-causal associations

according to the above criteria from a given strategy

model consisting of nomothetic cause-and-effect hy-

potheses. The next section develops an appropriate

approach for the automated proof of causality.

3 PROOF OF CAUSALITY

BETWEEN BUSINESS

VARIABLES

The analysis and deﬁnition of a homogeneous notion

of causality in the preceding section of this paper rep-

resents the conceptual basis for the construction of

proven causal models for strategic decision support.

A set of nomothetic cause-and-effect hypotheses con-

tained in a rudimentary cause-and-effect model has to

be given by strategic decision makers and represents

the ﬁrst necessary causal property of a priori know-

ledge.

As HIL LBR AND proposes in his meta-model (Hill-

brand, 2003b), the key modeling element of this

model-type is an indicator which can be of crisp or

fuzzy type. These indicators are linked by either un-

deﬁned or deﬁned inﬂuence relations, where the latter

is described by axiomatically determined rules (e.g.:

ROI, ROCE, etc.).

Consequently it is the focus of this section to pro-

vide appropriate methods in order to analyze the hy-

pothetically established undeﬁned inﬂuences within

a strategic DSS with respect to their causal validity.

This task of the proposed approach is to detect so-

called α-errors of undeﬁned nomothetic cause-and-

effect hypotheses between variables. Therefore the

starting point for the reconstruction of a proven causal

model is a rather overdeﬁned rudimentary model as

described above.

In order to analyze the causality criterion of infor-

mational redundancy it seems to be suitable to re-

strict to the linear case as this proof per se does not

build the model base but is used to select variables for

BUILDING PROVEN CAUSAL MODEL BASES FOR STRATEGIC DECISION SUPPORT

179

the following approximation of arbitrary causal func-

tions. The admissibility of this theory for different

types of causal functions has been shown by HIL L-

BR AND (Hillbrand, 2003a, pp. 299ff.).

When considering the third necessary condition for

causality of temporal precedence between cause and

effect, the inadequacy of the concept of correlation

alone to prove cause-and-effect relations becomes ob-

vious: The correlation of two time series would show

that the variations of an independent and a dependent

variable are similar and that they take place contem-

poraneously. As this is mutually contradictory to the

notion of causality as deﬁned in the previous section,

the concept of correlation has to be adopted to mea-

sure temporally lagged responses of the variation of

an independent factor within the time series of the

dependent variable. Therefore the cross-correlation

X,Y

(∆t) implies a time lag ∆t between a cause X

and an effect Y in the following form:

X,Y

(∆t) =

t=1

−

Y )(x

t−∆t

−

· σ

(1)

Where y

and x

stand for the values of the vari-

ables Y and X at time t,

X and

Y for the average

values and σ

as well as σ

for the standard devia-

tion of the respective time series.

By calculating the cross correlations for varying

time lags it is possible to identify a window of im-

pact between an independent and a dependent vari-

able (characterized by a minimum time lag and a

number of subsequent effects). For this purpose it is

necessary to determine the statistical signiﬁcance of

a cross correlation at a given time lag. Therefore this

approach uses BART LET T’s signiﬁcance test (Bartlett,

1955) following the suggestions of the appropriate lit-

erature in this area (Levich and Rizzo, 1997, p. 6):

The null hypothesis that two given time series at a

certain time lag are independent has to be rejected if

the following constraint is satisﬁed:

|ρ

X,Y

(∆t)| >

n − |∆t|

(2)

Where n stands for the number of samples in the time

series of X and Y , respectively.

By increasing the time lag ∆t by discrete steps be-

ginning at a lag of zero time periods, it is possible to

identify the minimum time lag by recording the ﬁrst

signiﬁcant cross correlation between the time series.

This approach is illustrated in ﬁgure 1 for the fol-

lowing synthetically generated time series:

= ε

U(0;1)

(3)

= 0.2y

t−1

+ 0.5x

t−2

+ 0.2x

t−3

+ 0.1ε

U(0;1)

(4)

Where ε

U(0;1)

is a random variable uniformely dis-

tributed between zero and one.

As it is obvious from the above equations, the time

series y

of the independent variable Y incorporates

past values of the time series x

with a time lag of

two and three time periods, respectively. Therefore

the correct window of impact is [2, 3].

-0,2

-0,1

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

0 1 2 3 4 5 6 7 8 9

∆

(

∆

Figure 1: Correlogram between two timeseries

Figure 1 shows the cross correlations computed

from the artiﬁcial time series x

and y

for the time

lags ∆t = 0, . . . , 9, as well as the bandwidth of

their standard deviation which lies between the dot-

ted lines. The clear consequence which can be drawn

from this correlogram is that the ﬁrst signiﬁcant cor-

relation starting from zero occurs at a time lag of

∆t = 2 which corresponds exactly to the generating

function of y

as stated above.

The ﬁrst attempt to determine the appropriate

length of the window of impact using the correlo-

gram in ﬁgure 1 yields time lags between ∆t = 2

and ∆t = 4. Hence it can be shown that signiﬁcant

autocorrelation of the independent time series leads to

the so-called echo effect (Hillbrand, 2003a, pp. 178f.)

which describes the indirect effects of independent

values prior to the window of impact through an au-

tocorrelated dependent time series: In the example of

ﬁgure 1 the term ”. . . 0.2y

t−1

. . . ” leads to a reﬂec-

tion of x

t−3

and x

t−4

within the time series of y

Therefore it is crucial for a correct identiﬁcation of

the impact window to eliminate any autocorrelation

within the time series to be analyzed. Since a disqui-

sition of these so-called prewhitening approaches ex-

ceeds the limits of this paper, it remains to refer to the

appropriate literature (Hillbrand, 2003a, pp. 181ff.).

Potentially causal relations which show a signiﬁ-

cant window of temporally lagged impact are subject

to a further analysis of common causation by third

variables. For this purpose PEAR L and VERMA pro-

pose an approach to identify spurious associations in-

duced by a common cause (Pearl and Verma, 1991):

Theorem 2 (Controlling for third variables): One

can assume a relation X → Y to be causal if

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

180

and only if the time series of the potential effect Y

incorporates not only patterns of its direct potential

cause X but also those of the predecessors P of X

in the cause-and-effect model. If X and Y as well

as P and X are informationally redundant but P

and Y are not, an unknown third variable U rather

than a causal relation must be assumed to induce

informational redundancy between X and Y . ¤

As a consequence the patterns of P are reﬂected

within the time series of X but they are not inherited

on to Y due to the absence of a genuine cause-and-

effect relation X → Y .

A basic tool for the analysis of these assumptions

within causal graphs is the concept of conditional in-

dependence: Two variables A and B are conditionally

independent given a set of variables S

- written as

(A ⊥ B | S

) - if A and B are informationally re-

dundant. However, if the impacts of S

on B are

eliminated, this property vanishes. Therefore S

said to ”block” the causal path between A and B.

The theory to detect third variable effects as out-

lined in this paper is implemented by the IC

Algorithm. For reasons of lucidity, this paper dis-

penses with a detailed discussion of these proce-

dures but refers to the appropriate literature (Pearl and

Verma, 1991) or (Hillbrand, 2003a, p. 198).

Summarizing this approach, the modeling of

nomothetic cause-and-effect hypotheses by decision

makers represents a prerequisite for their proof as

well as the ﬁrst causality criterion. The second and

third condition for causality - informational redun-

dancy and temporal sequence - are tested by analyz-

ing the cross correlations between the prewhitened

time series of the respective variables connected by a

cause-and-effect hypothesis. To rule out a third vari-

able inducing informational redundancy between two

lagged variables, this analysis is completed by the ap-

plication of the IC-Algorithm as outlined above. Only

relations which pass all these tests satisfy the neces-

sary causality conditions and are therefore said to be

genuinely causal.

4 APPROXIMATION OF

UNKNOWN CAUSAL

FUNCTIONS

The proof of causality as proposed in the previous

section is the main prerequisite for the approximation

of the unknown causal function affecting the values

of any arbitrary business variable within a cause-and-

effect structure. This provides the necessary numeric

properties for the causal model base of a DSS to run

IC = Inductive Causation

numeric analyses (e.g.: simulation, how-to-achieve or

what-if-analyses).

Many function approximation techniques either re-

quire a priori knowledge about basic functional de-

pendencies (e.g.: regression analysis) or their approx-

imation results are only valid within rather tight lo-

cal boundaries (e.g.: FOU RIE R or TAYLOR series ex-

pansion). Since the form of these cause-and-effect-

functions cannot be assessed a priori it is necessary

to employ so-called universal function approximators

for the purpose as described above (Tikk et al., 2001).

Hence these techniques are able to learn any arbitrary

function from mere empirical observations without

the need to narrow down some base function. As it

can be shown, microeconomic functions which usu-

ally underly strategic reasoning are almost never of

linear type (Hillbrand, 2003a, pp. 201ff.). The rea-

sons for this observation are manifold: Saturation as

well as scale effects or resource limitations are only

a few issues. One well-known example is the associ-

ation between the market price and the customer de-

mand for a certain product: Lowering prices will not

linearly result in an increasing demand. Rather this

association is expected to follow some S-shaped - also

known as sigmoidal or logistic - pattern (Allen, 1964).

For these reasons it is essential to abandon all re-

strictions regarding a priori assumptions about the

unknown function underlying a cause-and-effect re-

lation. Therefore this approach studies the potential

and limitations of Artiﬁcial Neural Networks (ANNs)

for universal causal function approximation. The cen-

tral theory in this area has been proposed by KOL-

MO GOROV who proved that any arbitrary unknown

function f can be approximated by two nested known

functions (Kolmogorov, 1957). Further enhance-

ments of KOLMOGOROV’s superposition theory have

been developed by several authors which lead to the

notion of ANNs as universal function approximators

(Hillbrand, 2003a, pp. 210 – 215).

Since this universal approximation property has

been proved for numerous of types of ANNs, this

approach focuses on the construction of MLPs out

of empirically proven cause-and-effect hypotheses.

Therefore the causal strategy model has to be sepa-

rated into causal function kernels (CFK). The latter

describe a set of variables and interjacent cause-and-

effect relations, each of which consists of a depen-

dent element and its direct predecessors. Following

the theory underlying this approach, the totality of

all cause-and-effect relations within a causal function

kernel represent the unknown causal function deter-

mining the values of the dependent variable.

Due to the possible existence of indirect associa-

tions between independent and dependent variables

within a CFK - also known as multicollinearity - it

is likely that the overall effect between two such ele-

ments has to be separated in order to obtain the direct

BUILDING PROVEN CAUSAL MODEL BASES FOR STRATEGIC DECISION SUPPORT

181

share of inﬂuence. Hence it is necessary to extend the

causal function kernels for cause-and-effect relations

which directly and/or indirectly link two independent

variables X

→ X

. These auxiliary cause-and-effect

relations accounting for multicollinearity can be dis-

covered by analyzing the transitive closure of each in-

dependent variable within the global causal system:

For every pair of independent variables X

and X

within a causal function kernel K

there exists an

auxiliary cause-and-effect relation X

Ã X

if and

only if X

is contained in the transitive closure of X

according to the global model G as shown in ﬁgure 2.

Figure 2: Separation of (extended) causal function kernels

Since an unknown causal function to be approxi-

mated does not exist between variables but rather be-

tween their lagged time series, the (e)CFKs have to

be temporally disaggregated. While the dependent

variable Y is represented by its instantaneous time se-

ries y

as an output node, each independent variable

leads to a number of input nodes corresponding to the

length of the appropriate window of impact (see sec-

tion 3). As far as eCFKs are concerned, it is necessary

to introduce a second input layer which accounts for

auxiliary cause-and-effect relations: The time series

of the second layer are derived by the same procedure

as described above taking the inﬂuenced indirect time

series of the auxiliary association as output node and

the inﬂuencing element as input node. Second input

layer elements which affect ﬁrst layer time series and

the output node directly are of speciﬁc interest since

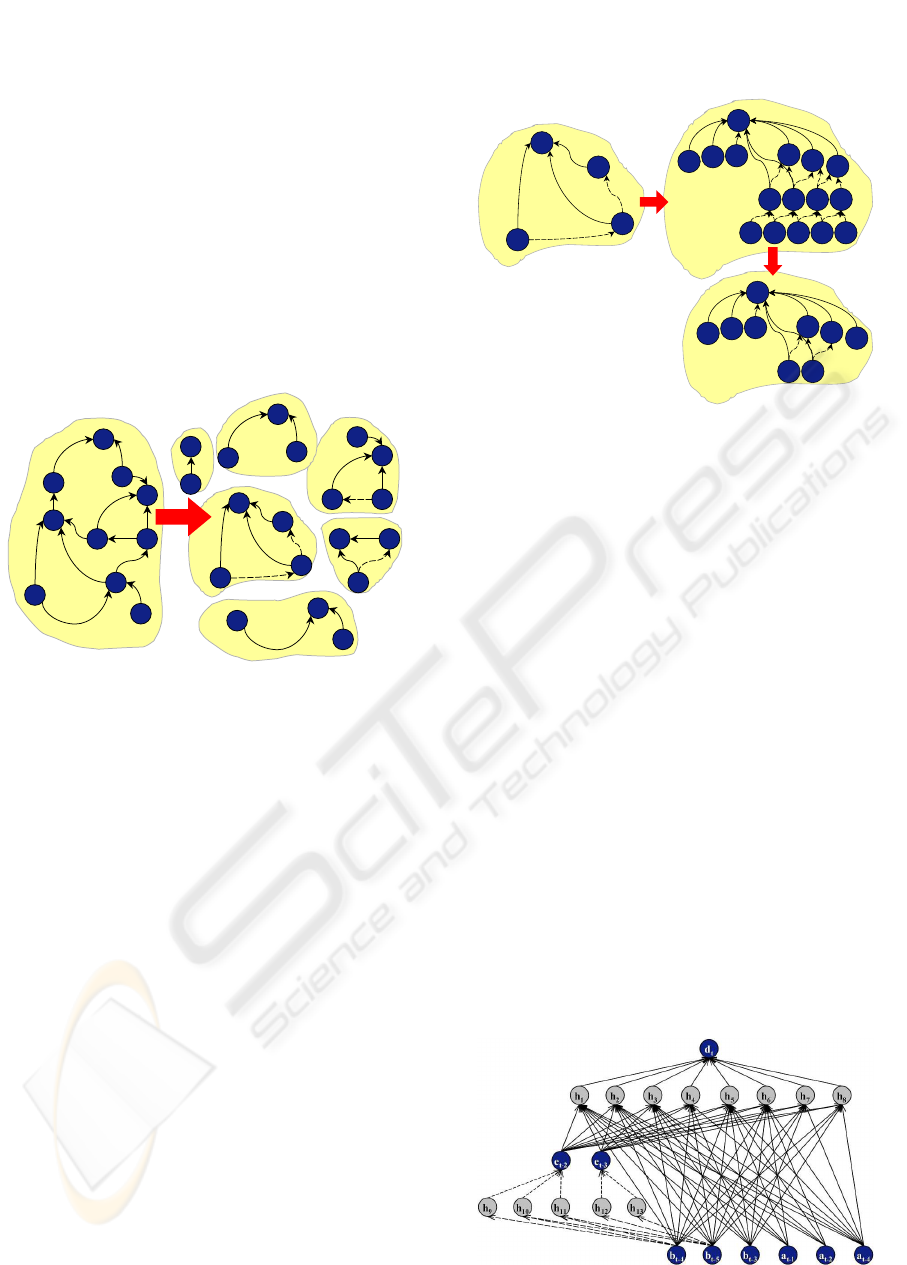
they combine direct and indirect inﬂuence as ﬁgure 3

shows for the extended causal function kernel K

As temporal disaggregation delivers the appropri-

ate input and output nodes for a neural function ap-

proximator in the form of temporally lagged time se-

ries there remains the issue to complete the model se-

lection of the ANN. This includes an adequate dimen-

sioning of the hidden layer(s) as well as the selection

of input and transfer functions for all ANN-nodes.

Since the universal approximation property pos-

tulates a limitation of the inner function of KOL-

t-3

[1,2]

[3,5]

[2,4]

[1,2]

[2,3]

t-4

t-2

t-1

t-2

t-3

t-5

t-4

t-6

t-7

t-5

t-6

t-7

t-8

t-9

t-3

t-4

t-2

t-1

t-2

t-3

t-5

t-4

Figure 3: Temporal disaggregation of (e)CFKs

MO GOROV’s theorem, it is necessary to use so-called

squashing functions which encompass sigmoid as

well as logistic, sine or heaviside functions (Hill-

brand, 2003a, p. 214). For practical reasons the use

of an additive input function for hidden and output

neurons is recommended.

The selection of an appropriate number of hidden

neurons is directly related to the generalization abi-

lity of the ANN (i.e. to learn a certain function in-

stead of memorizing input-output mappings). As this

speciﬁc model selection task depends on a variety of

issues which cannot be analytically determined a pri-

ori, it is necessary to rely on heuristics (for details see

(Hillbrand, 2003a, pp. 226 – 230)) and evaluate the

prediction accuracy of the trained ANN by using a

validation data set.

As it follows from the temporal disaggregation of

eCFKs as discussed above, the resulting auxiliary

cause-and-effect relations between second-level and

ﬁrst-level time series have to be incorporated into the

neural function approximator in order to account for

indirect effects. Therefore auxiliary sub-MLPs are in-

troduced as symbolized by dotted connectors in the

example of ﬁgure 4.

Figure 4: Neural function approximator for (e)CFKs

Before the training of the overall causal function

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

182

approximator it is necessary to learn these correct-

ing functions, each of which has one ﬁrst-level time

series (e.g.: e

t−2

and e

t−3

) as output node and one

or more second-level time series as input nodes. Af-

ter the training of all correcting ANNs, their weights

are kept ﬁxed and included in the main neuron model.

For the overall training of the causal function approx-

imator it is necessary to equip ﬁrst-level nodes with a

speciﬁc input function since they are input and hidden

nodes in the same way. Consequently the input func-

tion of a ﬁrst level node calculates the weighted output

sum of all preceding nodes plus the respective input

value of the node itself. The ratio between these two

shares of cumulative input is needed for training pur-

poses when employing an error backpropagating al-

gorithm: The same portion by which the overall input

for a ﬁrst-level node consists of values from a lower

network layer is used to distribute the output error -

backpropagated from higher network levels - among

lower level neurons.

Since all further characteristics regarding layout

and training of neural causal function approximators

correspond with those of MLPs, they are not dis-

cussed in further detail.

Having determined the appropriate connection

weights for these neural function approximators re-

constructing a causal function , they can be used to ex-

plain the associations between business variables and

goals as well as for the prediction of future values for

dependent variables in a numeric way.

5 CONCLUSIONS

Experimental results with synthetically generated

time series of causally dependent business variables

have yielded the admissibility of the theoretic foun-

dations for this approach (Hillbrand, 2003a, pp. 288

– 319): All cause-and-effect relations implicitly con-

tained in the generating processes for ﬁve time se-

ries of an experimental case study could be recov-

ered from a fully interlinked causal system (i.e.: Ev-

ery variable is linked to all other elements) by analyz-

ing the four causality criteria and the falsiﬁcation of

all spurious associations. Studying the relevance of

anomalies for the results of this causality proof shows

its robustness against nonlinearity, multicollinearity

as well as autocorrelation within the causal function

kernels. The exposure to highly noisy causal asso-

ciations is the only issue which remains for future re-

search in this context as this seems to affect the results

of this causality validation approach negatively. The

neural approximation of the causal functions underly-

ing these proven cause-and-effect relations results in a

signiﬁcantly higher ex post prediction quality for the

validation set than various regression techniques.

REFERENCES

Allen, R. (1964). Mathematical Analysis for Economists.

St. Martin’s Press, New York (NY).

Bartlett, P. S. (1955). Stochastic Processes. Cambridge

University Press, Cambridge, UK.

Hillbrand, C. (2003a). Inferenzbasierte Konstruk-

tion betriebswirtschaftlicher Kausalmodelle zur Un-

terst

utzung der strategischen Unternehmensplanung.

Unpublished PhD Thesis, University of Vienna, Vi-

enna. (in German).

Hillbrand, C. (2003b). Towards the accuracy of cybernetic

strategy planning models: Causal proof and function

approximation. Journal of Systemics, Cybernetics and

Informatics, 1(2).

Hillbrand, C. and Karagiannis, D. (2002). Using artiﬁ-

cial neural networks to prove hypothetic cause-and-

effect relations: A metamodel-based approach to sup-

port strategic decisions. In Piattini, M., Filipe, J., and

Braz, J., editors, Proceedings of ICEIS 2002 - The

Fourth International Conference on Enterprise Infor-

mation Systems, volume 1, pages 367 – 373, Ciudad

Real, Spain.

Kaplan, R. and Norton, D. (2004). Strategy Maps: Convert-

ing Intangible Assets into Tangible Outcomes. Har-

vard Business School Press, Boston (MA).

Kolmogorov, A. N. (1957). On the representation of con-

tinuous functions of many variables by superposition

of continuous functions of one variable and addition.

Doklady Akademii Nauk SSSR, 114:953 – 956.

Levich, R. M. and Rizzo, R. M. (1997). Alternative tests

for time series dependence based on autocorrelation

coefﬁcients. In Stern School of Business, editor, Sym-

posium on Global Integration and Competition, New

York (NY).

Mendoza, C., Delemond, M.-H., Giraud, F., and Loening,

H. (2002). Tableaux de bord et Balanced Scorecards.

Guide de gestion RF. Publications ﬁduciaires. (in

French).

Pearl, J. and Verma, T. (1991). A theory of inferred cau-

sation. In Allen, J. A., Fikes, R., and Sandewall, E.,

editors, Principles of Knowledge Representation and

Reasoning, pages 441 – 452, San Mateo (CA).

Schnell, R., Hill, P. B., and Esser, E. (1999). Methoden

der empirischen Sozialforschung. Oldenbourg-Verlag,

Munich et al., 6

edition. (in German).

Schwaninger, M. (2001). System theory and cybernetics.

Kybernetes, 30(9/10):1209–1222.

Tikk, D., K

oczy, L. T., and Gedeon, T. D. (2001). Universal

approximation and its limits in soft computing tech-

niques. an overview. Research Working Paper RWP-

IT-02-2001, Murdoch University, Perth W.A.

Vester, F. (1988). The biocybernetic approach as a basis for

planning our environment. Systems Practice, 4:399 –

413.

BUILDING PROVEN CAUSAL MODEL BASES FOR STRATEGIC DECISION SUPPORT

183