STRATEGIC NEGOTIATION OF BANDWIDTH IN COOPERATIVE

NETWORKS

Jonathan Bredin

Colorado College

Department of Mathematics, 14 E Cache la Poudre St, Colorado Springs, CO 80903, USA

Keywords:

Cooperative networks, resource allocation, game theory, self-interested agents

Abstract:

We analyze the scenario where a pair of network devices each periodically relies on the other to handle network

trafﬁc. Without immediate reward, the forwarding device incurs an opportunity cost in handling the other’s

request. We ﬁnd, however, situations where rational decision makers prefer bandwidth exchange to isolated

operation. We base our analysis on a take-or-leave-it protocol inspired by the Rubinstein bargaining model,

and extend it to evaluate repeated interaction between pairs of devices.

1 INTRODUCTION

Around the world, wireless network users consoli-

date their resources to form cooperative networks to

extend the range of their wirelessly networked de-

vices (Flickenger, 2003). Devices in each of these

networks are owned by multiple self-interested in-

dividuals and each device depends on its peers to

handle some of its network trafﬁc. The deployment

cost for a cooperative network spreads evenly among

the many users. Many wireless cooperative networks

have emerged in urban neighborhoods around the

world. Furthermore, the distributed ownership and

policy development make cooperative networks po-

tentially dynamic and robust to ﬂuctuating user de-

mand and mobile nodes.

The network depends device owners devices to

choose to cooperate– there is no other motivation

for participation in the network. Most cooperative

networking organizations assume that users willingly

donate hardware to build the network, but we ﬁnd

that there are several reasons to question the assump-

tion. First, network applications require increasingly

greater bandwidth, especially in light of ubiquitous

multimedia, and bandwidth will become constrained.

Second, in the wake of recent denial-of-service at-

tacks from email viruses and worms, it is clear that

a networked commons could beneﬁt from some reg-

ulation. Finally, many obvious applications of coop-

erative networks exist in mobile wireless networks,

where devices face not only bandwidth, but also bat-

tery power constraints, so network participation may

not be rational.

This paper examines the motivations for peer-wise

bandwidth exchange in cooperative networks. We

ﬁnd that even a short-sighted analysis provides incen-

tive for rational decision makers to contribute to co-

operative networks. The equilibrium reached in the

myopic analysis, however, is not stable to perturba-

tion or incomplete information.

In section 2 we present our model for bandwidth

exchange. Section 3 describes the method that we

use to compare the bandwidth allocations. From the

evaluation and ideas from existing negotiation mod-

els, we derive a policy for one device to rationally de-

cide whether or not to share bandwidth with another

on the expectation of future cooperation. We describe

some relevant work in section 6 and conclude in sec-

tion 7 with directions to extend our analysis.

2 BANDWIDTH EXCHANGE IN

COOPERATIVE NETWORKS

That the cost of deployment falls evenly among the

network users motivates the construction of coopera-

tive networks. Users contribute devices to form the

network. Sometimes a device will link the coopera-

tive network to the rest of the Internet. Frequently, the

devices comprising a cooperative network are wire-

lessly linked using 802.11 protocols where most de-

230

Bredin J. (2004).

STRATEGIC NEGOTIATION OF BANDWIDTH IN COOPERATIVE NETWORKS.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 230-235

DOI: 10.5220/0002627302300235

 SciTePress

A B

network A network B

Figure 1: The network topology to be modeled.

vices could not individually connect to the Internet.

Several possible factors motivate Internet uplink

sharing. Distributing access of several uplinks among

network users spreads the load evenly among the up-

links. Users beneﬁt from statistical multiplexing: the

chance that all users require network access is small

and the residual network capacity can be divided

among the active users. The scenario also provides

redundancy when one user’s service provider fails to

provide Internet access due to link or router failure,

network overload, etc.

Another motivation may stem from that while co-

operating network members may be mobile, their up-

links are statically located. A user that strays far from

her Internet uplink may wish to use another uplink

during her travel. The user “pays” for her access

through providing other members with network ac-

cess when they travel near her uplink.

Finally, ﬁnancial reasons may motivate sharing of

a network uplink. Perhaps a group of users lives in a

building ill suited for network access; wiring the en-

tire building may be expensive or intrusive and users

could instead share a set of uplinks. In rural environ-

ments, a group of users may share a satellite uplink

that would be too expensive for a single user to main-

tain. The shared payment of the Internet service may

be arranged out of band, but to function, there must

be incentive for devices to contribute to the rest of the

network rather than freeload on the efforts of others.

This altruistic behavior, or at least the incentive to

behave as such, is a central obstacle for cooperative-

network operation. Forwarding network trafﬁc incurs

an opportunity cost of network bandwidth usage on

the part of altruistic devices, i.e. the more one de-

vice helps another, the less work it can perform for

itself. Rationally, donations come with some expecta-

tion that favors will be returned.

We model a scenario where two devices, A and B,

repeatedly query one another to forward network traf-

ﬁc. A link partitioning the network connects the two

devices. Device i connects to its side of the network

with an x

bit per-second link. Figure 1 sketches the

network topology. For now, we ignore the bandwidth

constraint of the connecting link as well as battery

limits.

Periodically, device j requests that i give it network

access. We assume that a device will not make an-

other request until the current request is satisﬁed. De-

vice j informs i the desired duration of usage; and

i immediately returns an answer of x

, the amount

of bandwidth it will provide to j.

If i denies j’s

request, no further exchange will occur between the

devices. We assume that there is no cost in dividing

bandwidth, so that

= x

+ x

. (1)

3 UTILITY MODEL

We now assert some general assumptions we make

that will drive the derivation of sharing policy in the

next section. Device i generates utility at a rate of

(x) per second, where u

is a continuous func-

tion of x, the amount of j’s bandwidth available for

i to consume. More bandwidth is always better, but

not proportionally so. Hence du

/dx is positive and

/dx

is negative. Without loss of generality, we

root the utility function so that u

(0) = 0. Further-

more, u

is onto with respect to the non-negative re-

als, modeling the belief that enough bandwidth will

solve any problem. We will use u

(x) = log(1 + x)

for the graphical and numeric examples for the re-

mainder of the paper.

We describe device i

s total utility as the sum of

two parts: the utility derived from local bandwidth

usage, and utility derived from consuming another de-

vice’s bandwidth. We write the expected utility func-

tion as

, x

) = α

) + (1 − α

)

), (2)

where α

is a weight in [0, 1] to determine the impor-

tance of local versus remote consumption. The func-

tions

and

represent the expected utility de-

rived from local and remote bandwidth, respectively.

Since bandwidth usage varies over time, we calculate

the time-discounted expected utility from each com-

ponent as a function of the estimated bandwidth con-

sumption presented in the next section.

3.1 Time-discounted evaluation

Devices prefer consuming earlier than later. We de-

ﬁne the value of i’s consumption of j’s bandwidth

from time t

until t

(x, t

, t

) =

(x)e

−tγ

dt =

(x)e

−tγ

(3)

For rest of the paper, the ﬁrst subscript of a bandwidth

amount denotes the provider, whereas the second, possibly

identical, subscript denotes the consumer.

STRATEGIC NEGOTIATION OF BANDWIDTH IN COOPERATIVE NETWORKS

231

where γ

∈ [0, 1] is i’s discount factor.

We now calculate the expected time-discounted

utility a device generates from consuming bandwidth.

For its own bandwidth, a device i values its choice to

consume x

bandwidth when it is requested, and x

at other times, as

(ˆx

) =

∞

r=0

∞

t=0

(r)p

(t)

, 0, t)

(ˆx

, t, t + r)

(ˆx

−γ

(t+r)

dt dr,

(4)

where we denote the probability density function for

the duration that j requests bandwidth from i as q

(r),

the inter-request time probability density function as

(t), and the estimate i has of using its own band-

width as ˆx

To simplify the calculation, we assume that each

device generates requests at a Poisson rate with ex-

ponentially distributed request durations, though our

decision model in section 4 does not depend on the

assumption. Under the Poisson assumption where de-

vice i has a request intensity of λ

and an average re-

quest duration of 1/φ

, the time-discounted expected

value of a device consuming its own bandwidth is

(ˆx

) =

(φ

+ γ

) + λ

(ˆx

)

(γ

+ φ

+ λ

)

. (5)

The calculation of the value device i has for con-

suming j’s bandwidth is a similar,

(ˆx

) =

∞

r=0

∞

t=0

(r)p

(t)

(ˆx

, t, t + r)

(ˆx

−γ

(t+r)

dt dr,

(6)

and the Poisson assumption simpliﬁes to the result

(ˆx

) =

(ˆx

)

(γ

+ φ

+ λ

)

. (7)

We note that, even without the Poisson assumption,

the utility of consuming no bandwidth is still zero.

3.2 Feasible allocations

For a cooperative network to function, a device must

be better off periodically sharing than operating in

Contact the author for a full version of the paper with

an appendix that shows that both

and

are increasing-

concave in the utility consumed.

0.5

1.5

2.5

0 0.2 0.4 0.6 0.8 1

xji

xii

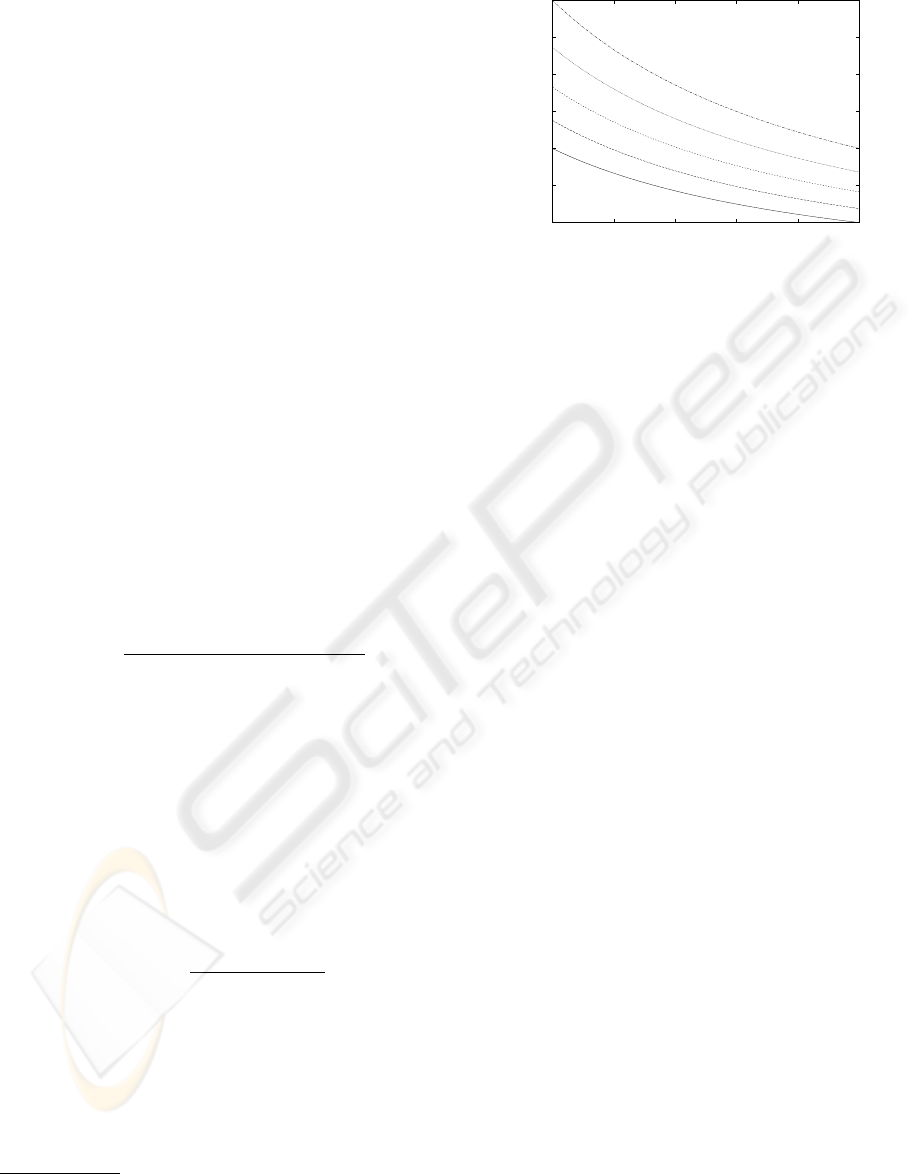
Figure 2: Five isoquants of i’s bandwidth and j’s bandwidth

donated to i. The lowest curve represents the set of alloca-

tions for which i is indifferent to sharing or acting on its

own. The highest curve represents a set of allocations that

yield twice as much utility to i than operating in isolation.

isolation and consuming only it its own bandwidth. In

this section we model a device’s preference for con-

suming its own bandwidth in comparison to its part-

ner’s. We use the comparison to derive the set of ratio-

nally feasible bandwidth allocations from which the

devices may agree.

Let us assume that devices attempt to maximize a

weighted sum of their valuations for bandwidth usage,

(ˆx

, ˆx

) = α

− ˆx

) + (1 − α

)

(ˆx

(8)

where α

∈ [0, 1] expresses i’s preference for local

versus remote bandwidth usage.

An isoquant is a set of equally preferable alloca-

tions. As a result of modeling utility as an increas-

ing function of bandwidth with diminishing returns,

the curves representing isoquants of two commodi-

ties will always be convex.(Mas-Colell et al., 1995)

We plot some isoquants for a device’s preference for

bandwidth in ﬁgure 2. The lowest curve represents the

set of allocations that are all equally preferable to op-

erating without cooperation between the two devices.

It would not be rational for a device to operate with

the expectation of receiving an allocation lying under

the lowest curve.

Since we assume that dividing bandwidth is cost-

less, we can rearrange the isoquant curves in ﬁgure 2

in terms of x

= x

− x

and x

. We can also do

the same for j’s indifference curves and plot the two

devices’ isoquants against each other. Figure 3 plots

each device’s isoquant curves at the level of utility

indifferent to isolated operation. The ﬁgure demon-

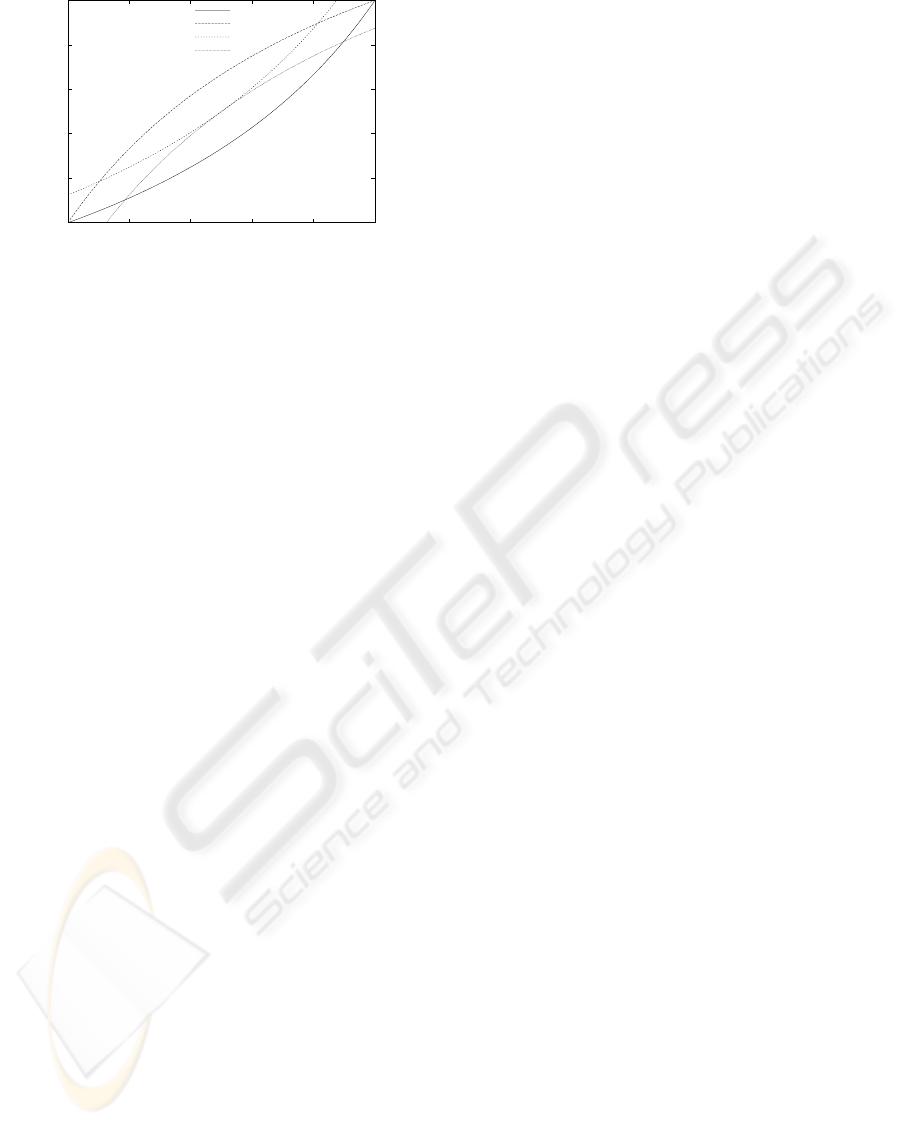
strates the set of feasible bandwidth allocations.

The lens-shaped region between the two curves

represents a set of allocations with which both de-

vices prefer sharing to isolated operation. With any

ICEIS 2004 - SOFTWARE AGENTS AND INTERNET COMPUTING

232

0.2

0.4

0.6

0.8

1.2

1.4

0 0.2 0.4 0.6 0.8 1 1.2 1.4

xij

xji

j’s constraint

i’s constraint

Figure 3: The set of feasible allocations is the lens shaped

area between the curves. Device i will opt to consume only

its own bandwidth if the allocation falls on the left side of

its constraint curve, whereas j will only consume above its

constraint curve.

other allocation, one device would prefer to opt out

of cooperation. We use this area to derive a rational

bandwidth-sharing policy in the next section.

4 NEGOTIATION

We now use the utility model to derive a rational pol-

icy to share bandwidth with another device. The de-

vices repeatedly ask each other for assistance. After

several exchanges, device i has an expectation of re-

ceiving ˆx

bandwidth and giving ˆx

when necessary.

We use a rationale taken from the Rubinstein bar-

gaining model: in bargaining, an agent offers its part-

ner an allocation whose outcome the partner is in-

different to accepting or not (Rubinstein, 1982). If

we assume that the impact of the next interaction is

negligible– perhaps the devices are mobile and will

move on anyway– then a device will offer its partner

an allocation that the other device prefers equally to

solo operation. The allocation satisﬁes

(ˆx

, x

) = U

, 0). (9)

Figure 3 sketches with a solid line the offer that i

makes to j as a function of j’s generosity to satisfy

equation 9. We can solve for the the lower boundary,

device i’s response as a function of j’s cooperation,

(ˆx

) =

−1

(

)−γ

−ˆx

)

(1−α

)γ

(10)

In the example where utility generation is a loga-

rithmic function of bandwidth, we derive the bound-

ary

= h

(ˆx

) = u

−1

) − u

− ˆx

))),

(11)

where

(γ

+ φ

+ λ

)

(1 − α

)λ

(γ

+ φ

+ λ

)

. (12)

With the rationality constraint that i may prefer to

share less than the amount required to sustain trade

with j, and i reverts back to its own constraint. At

this extreme case, i’s response is simply the inverse

of j’s initial response. We incorporate the two cases

to yield i’s response g

(ˆx

) =

(ˆx

) U

(ˆx

), ˆx

) ≥ U

(0, x

)

−1

) U

(ˆx

), ˆx

) < U

(0, x

)

(13)

We can visualize i’s response as the lower boundary

of the two curves plotted in ﬁgure 3.

5 EQUILIBRIUM

It is useful not only to know how devices immediately

share bandwidth, but also whether they will continue

to share bandwidth. To this end, we study equilib-

rium behavior to derive conditions under which de-

vices will exchange bandwidth. Furthermore, equi-

libria stability also interests us; we wish to know how

small changes in exchange affect exchange decisions.

We describe equilibrium as the pair of responses

such that the equality

= g

)) (14)

holds. Notice that with the response derived in the

previous subsection, the trivial equilibrium at x

= 0 is always feasible, but sometimes other equi-

libria exists. We treat the composition from equa-

tion 14 as an iterated function system to determine

equilibria and their stability. A necessary and sufﬁ-

cient condition for stability of an equilibrium is that

the absolute slope of the iterated function system is

less than one (Kaplan and Glass, 1995). With our sce-

nario, the condition becomes

1 >

))

. (15)

The intuition is that when the absolute slope is less

than one, changes in a device’s output cause the other

device to respond, but to a lesser extent. An absolute

slope greater than one means that one device’s change

is magniﬁed by its partner, and the equilibrium is un-

stable.

STRATEGIC NEGOTIATION OF BANDWIDTH IN COOPERATIVE NETWORKS

233

We rewrite a device’s response function as

) = min{h

), h

−1

)}. (16)

Note that because h

is continuous and convex, there

is a second equilibrium where h

and h

−1

intersect

beyond x

= 0. Additionally, i’s partner shares the

same intersection. The allocation represented at the

allocation yields utility for each device equal to not

sharing any bandwidth, so the rationality constraint is

enforced for each device. Let us name the equilibrium

where h

= h

−1

as (x

∗

, x

∗

) and deﬁne

k = x

∗

. (17)

We now will use k to show that allocations to the

right of the second equilibrium will result in allo-

cations closer to to it, and allocations to the left of

the equilibrium will result in devices eventually boy-

cotting trade.

Theorem 1 The equilibrium (x

∗

, x

∗

) attracts allo-

cations (x

, g

)) whenever x

> x

∗

Proof. We prove the theorem by showing that the

slope of the iterated response g

)) is strictly

less than one. Since each device’s rationality con-

straint is increasing concave in the amount it receives

from its partner, k provides a boundary on the slope of

each device’s response. The ratio k provides a strict

upper bound on i’s marginal response, and 1/k is the

strict upper bound for j’s marginal response. Addi-

tionally, both these marginals are positive, since the

constraints are strictly increasing. Hence for x

∗

˙g

< k ∗ 1/k = 1, (18)

so the equilibrium (x

∗

, x

∗

) is attractive from the

right since the derivative of the iterated response is

less than one, but greater than zero. ¦

Theorem 2 The equilibrium (x

∗

, x

∗

) repulses allo-

cations (x

, g

)) whenever x

< x

∗

Proof. We use a similar argument to show that the

marginal iterated response is greater than one when

is less than x

∗

. Note that the devices’ response

functions are increasing convex for the values of inter-

est and that g

(0) = 0. Again, k provides a bound for

marginal response near the equilibrium (x

∗

, g

∗

)).

This time, dg

/dx

> k and dg

/dx

> 1/k, so

˙g

> k ∗ 1/k = 1. (19)

Hence, from the left, the equilibrium (x

∗

, g

∗

)) is

repulsive. ¦

While there is an equilibrium that involves both de-

vices exchanging bandwidth, the devices are indiffer-

ent to the equilibrium and not sharing. Furthermore,

the equilibrium is unstable in the sense that deviations

in exchange always yield less trade.

6 RELATED WORK

Rubinstein presents the seminal bargaining model

where two agents take turns proposing allocations to

each other (Rubinstein, 1982). When the total value

to be allocated decays over time, the scenario ends

with a ﬁnite number of iterations. Kraus applies the

Rubinstein model to solve automated service negoti-

ation problems (Kraus, 2001). Muthoo studies situa-

tions where agents repeatedly enter negotiations with

each other (Muthoo, 1999). He only considers sce-

narios where agents alternate taking turns in initiating

negotiation, and ﬁnds that when when agents have the

opportunity to make only one offer, as in our model,

that devices receive all or nothing.

The idea that networks can beneﬁt from coopera-

tive behavior is not new to this paper. Padmanab-

han and Sripanidkulchai analyze network traces of

news-ﬂash trafﬁc to create routing policies where de-

vices cooperate to reduce latency of network broad-

casts (Padmanabhan and Sripanidkulchai, 2002).

Buttyan and Hubaux observe that devices may

not wish to cooperate, but noncooperation eliminates

many applications (Buttyan and Hubaux, 2003). They

explore the possibility of embedding trusted hardware

into every network device. The trusted hardware en-

forces that each device may not use the network for

its own purposes more than it forwards other devices’

messages. They present several policies to optimize

local performance under the management of the cen-

soring trusted hardware.

Recently, several research groups have addressed

incentive problems for participation in peer-to-peer

ﬁle-sharing applications, focusing on modeling in-

centives through repeated multi-player prisoners’

dilemma games. Lai et al. measure the value of pri-

vate versus shared reputation information (Lai et al.,

2003). Their model addresses “whitewashing,” the

possibility that a device can change its identity for

each network interaction, and shows that systems

that rely on private reputation information do not

scale well. Ranganathan et al. compare reputa-

tion and market-based incentive mechanisms to ﬁnd

scenarios where reputation-based model performance

approaches the performance of market-based mod-

els (Ranganathan et al., 2003).

7 DISCUSSION

We present a pessimistic model for network exchange

to show that there exist equilibria allocations where

ICEIS 2004 - SOFTWARE AGENTS AND INTERNET COMPUTING

234

0.2

0.4

0.6

0.8

0 0.2 0.4 0.6 0.8 1

xij

xji

j’s constraint

i’s constraint

Ui’

Uj’

Figure 4: The set of feasible allocations and device i and j’s

isoquants that include the allocation that maximizes social

surplus.

rational devices choose to cooperate with one another.

The model is pessimistic in that each device myopi-

cally assumes that its actions will not affect its part-

ner’s future decision, except to wholesale discontinue

trading.

We note that there are frequently better allocations

than the ones that our model arrives. Figure 4 sketches

the set of feasible allocations as well as two new iso-

quants for the devices that maximize the sum of the

devices’ utilities– the social surplus.

We have two reasons to have optimism regarding

more efﬁcient allocation. First, more-forward look-

ing models will likely yield allocations lying deeper

into the lens-shaped region. We are currently inves-

tigating negotiation models where each device rea-

sons about the effects its own offer has in driving the

pair of devices towards a favorable equilibrium allo-

cation. Muthoo discovers that agents that alternate

positions in repeated bargaining situations strive for

more socially optimal allocations whereas in the tradi-

tional single-shot bargaining game, a device receives

more resources the less it values the resource as a re-

sult of brinksmanship. In Muthoo’s repeated bargain-

ing model, the reverse, more socially efﬁcient, effect

manifests (Muthoo, 1999).

The second source of intuition seems paradoxical:

competition will drive allocations to which devices

strongly prefer over not sharing. The idea is that given

the choice of sharing with two devices, a rational de-

cision maker will choose the one that yields a more

desirable allocation. So far, we have only modeled bi-

lateral bandwidth exchange. That competition might

provide sweeter allocations gives us further incentive

to continue our research. It is likely that testing mul-

tilateral exchange will be beyond scope of an analytic

model, so we are currently implementing our band-

width allocation policies inside the ns network simu-

lator.

That even a pessimistic model can motivate devices

to exchange bandwidth motivates us to further study

incentives for participation in cooperative networks.

We are excited to investigate foresighted models of

exchange as well as multilateral exchange to motivate

more efﬁcient exchange and to study larger networks.

REFERENCES

Buttyan, L. and Hubaux, J.-P. (2003). Stimulating cooper-

ation in self-organizing mobile ad hoc networks. Mo-

bile Networks and Applications, 8(5). to appear.

Flickenger, R. (2003). Building Wireless Community Net-

works, 2nd Edition. O’Reilly, Sebastopol, CA.

Kaplan, D. and Glass, L., editors (1995). Understanding

Nonlinear Dynamics. Springer Verlag, New York, NY.

Kraus, S. (2001). Strategic Negotiation in Multiagent Envi-

ronments. MIT Press, Cambridge, MA.

Lai, K., Feldman, M., Stoica, I., and Chuang, J. (2003).

Incentives for cooperation in peer-to-peer networks.

In Proceedings of the First Workshop on Economics

of Peer-to-Peer Systems.

Mas-Colell, A., Whinston, M. D., and Green, J. R. (1995).

Microeconomic Theory. Oxford University Press,

New York, NY.

Muthoo, A. (1999). Bargaining Theory with Applications.

Cambridge University Press, Cambridge, UK.

Padmanabhan, V. K. and Sripanidkulchai, K. (2002). The

case for cooperative networking. In Druschel, P., ,

Kaashoek, F., and Rowstron, A., editors, Peer-to-Peer

Systems, pages 178–190. Springer-Verlag, New York,

NY.

Ranganathan, K., Ripeanu, M., Sarin, A., and Foster, I.

(2003). To share or not to share: An analysis of in-

centives to contribute in collaborative ﬁle sharing en-

vironments. In Proceedings of the First Workshop on

Economics of Peer-to-Peer Systems.

Rubinstein, A. (1982). Perfect equilibrium in a bargaining

model. Econometrica, 50(1):97–109.

STRATEGIC NEGOTIATION OF BANDWIDTH IN COOPERATIVE NETWORKS

235