AN ADAPTABLE TIME-DELAY NEURAL NETWORK TO

PREDICT THE SPANISH ECONOMIC INDEBTEDNESS

M. P. Cuellar, W. Fajardo, M.C. Pegalajar, R. Pérez-Pérez

Dpt. Computer Science of University of Granada, Periodista Daniel Saucedo Aranda s/n,Granada,Spain

M.A. Navarro

Dpt. Economía Financiera y Contabilidad, Campus Universitario de la Cartuja, Granada, Spain

Keywords: Neural Network, Training, Time-Delay Neural Network, Levenberg-Marquardt

Abstract: In this paper, we study and predict the economic indebtedness for the autonomic of Spain. In turn, we use

model of neural network. In this study, we assess the feasibility of the Time-Delay neural network as an

alternative to these classical forecasting models. This neural network permits accumulate more values of

pass and a best prediction of the future. We show the MSE assignment to check the good forecasting of

indebtedness economic.

1 INTRODUCTION

Artificial Neural Networks (ANNs) have been

deployed in a variety of real world problems

(Haykin (1998)). The success of ANNs for a

particular problem depends on the adequacy of the

training algorithm regarding the necessities of the

problem. The existing gradient-based techniques in

particular the Back-propagation algorithm, have

been widely used in the training of ANNs.

A feed-forward neural network with an arbitrary

number of neurons can approximate some uniformed

continuous functions (Hornik et at.(1989)). These

arguments permit us the basic motivation to use

neural network for forecasting time series.

In this paper, we study the way to predict the

Spanish economic indebtedness for 2001 year. We

use the gross inner product of each community.

This paper is organized as follows. Section 2 we

introduce Time-Delay neural network. In Section 3,

we expose the adaptation algorithm, Levenberg-

Marquardt. So, Section 4 we show ours experimental

results in the application of this model with

autonomous Spain indebtedness. Finally, our

conclusions are presented in Section 5.

2 A TIME DELAY NEURAL

NETWORK

The traditional model of multi-layers neural network

is formed by a set of layers with artificial neurons.

Neurons of one layer is connected with each one of

neurons the following layers, so they are completely

connected. In figure 1, we show a neuron that it

appertains to layer l+1 of the network. The inputs

to the neuron in layer l are multiplied by the

weights

. These weights represent the synaptic

connection between the neuron i in previous layer

and neuron j in layer l+1. The output of neuron is

calculated through a sigmoidal function of the

weighty sum of its inputs:

iji

fwx

⎛⎞

⎜

⎝⎠

∑

⎟

(1)

Figure 1: Representation of a neuron

457

P. Cuellar M., Fajardo W., C. Pegalajar M., Pérez-Pérez R. and Navarro M. (2004).

AN ADAPTABLE TIME-DELAY NEURAL NETWORK TO PREDICT THE SPANISH ECONOMIC INDEBTEDNESS.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 457-460

DOI: 10.5220/0002628604570460

 SciTePress

The

=1 is the bias for neuron. The training of

network is realized through the Back-Propagation

algorithm.

To handle the temporal information (time

patterns) for the times series data, a neural network

must be “short-term memory”, the primary role of is

to remember the past signal. There are two attributes

of memory structure: depth and resolution. The

memory depth defines the length of the time window

available in the memory structure to store past

information. The deeper the memory, the further it

holds information from the past. Memory resolution

defines how much information will be remembered

in a given time window. The so-called “tapped delay

line” is the simplest and most commonly used form

of “short-term memory”.

A popular neural network that uses ordinary time

delays to perform temporal processing the so-called

time delay neural network (TDNN), which was first

described in Lang and Hinton (1988) and Waibel et

al. (1989). The TDNN is a multilayer feedforward

network whose hidden neurons and output neurons

are replicated across time. It was devised to capture

explicitly the concept of symmetry time as

encountered in the recognition of an isolated word

(phoneme) using a spectrogram.

The main goal in development of TD-neural

networks was to have a neural network architecture

for non-linear feature invariant classification under

translation in time or space. TD-Networks uses

built-in time-delay steps to represent temporal

relationships. The invariant classification translation

is realized by sharing the connection weights of the

time delay steps. The activation of each TD-neuron

is computed by the weighted summation of all

activations of predecessor neurons in a input

window over time and applying a non-linear

function (i.e. a sigmoid function) to the sum.

Time-Delay neural network (TDNN) is a

dynamic neural network structure that is constructed

by embedding local memory (tapped delay line

memory) in both input and output layers of a

multilayers feed forward neural network. Both, its

input and output are time series data.

3 GRADIENT DESCENDENT:

LEVENBERG-MARQUARDT

Like the quasi-Newton methods, the Levenberg-

Marquardt algorithm was designed to approach

second-order training speed without having to

compute the Hessian matrix. When the performance

function has the form of a sum of squares (as is

typical in training feedforward networks), then the

Hessian matrix can be approximated as

and the gradient can be computed as

where the Jacobian matrix that contains first

derivatives of the network errors respect to the

weights and biases, and

e is a vector of network

errors. The Jacobian matrix can be computed

through a standard Backpropagation technique that

is much less complex than computing the Hessian

matrix.

The Levenberg-Marquardt algorithm uses this

approximation to the Hessian matrix in the following

Newton-like update:

When the scalar µ is zero, this is just Newton's

method, using the approximate Hessian matrix.

When µ is large, this becomes gradient descent with

a small step size. Newton's method is faster and

more accurate near an error minimum, so the aim is

to shift towards Newton's method as quickly as

possible. Thus, µ is decreased after each successful

step (reduction in performance function) and is

increased only when a tentative step would increase

the performance function. In this way, the

performance function will always be reduced at each

iteration of the algorithm.

We use the algorithm implemented by

MATLAB. TRAINLM can train any network as

long as its weight, net input, and transfer functions

have derivative functions. We use the version 6.5

of MATLAB and toolbox of neural network with a

license of campus available in Universidad of

Granada.

4 RESULTS

To continue, we apply this model of neural network

to resolve the problem of forecasting of indebtedness

economic of the autonomous community Spanish in

the period between year 1986 and 2000. We have a

set of values of each community. These values

reflect the ratio of indebtedness. The TDNN utilized

is formed by 20 neuron input and a neuron output.

Moreover, we utilized three step delay in the input

layer.

In the following figure are represented the real

values (blue) and the predicted values (red). The

sixteen value is the prediction to year 2001. The axis

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

458

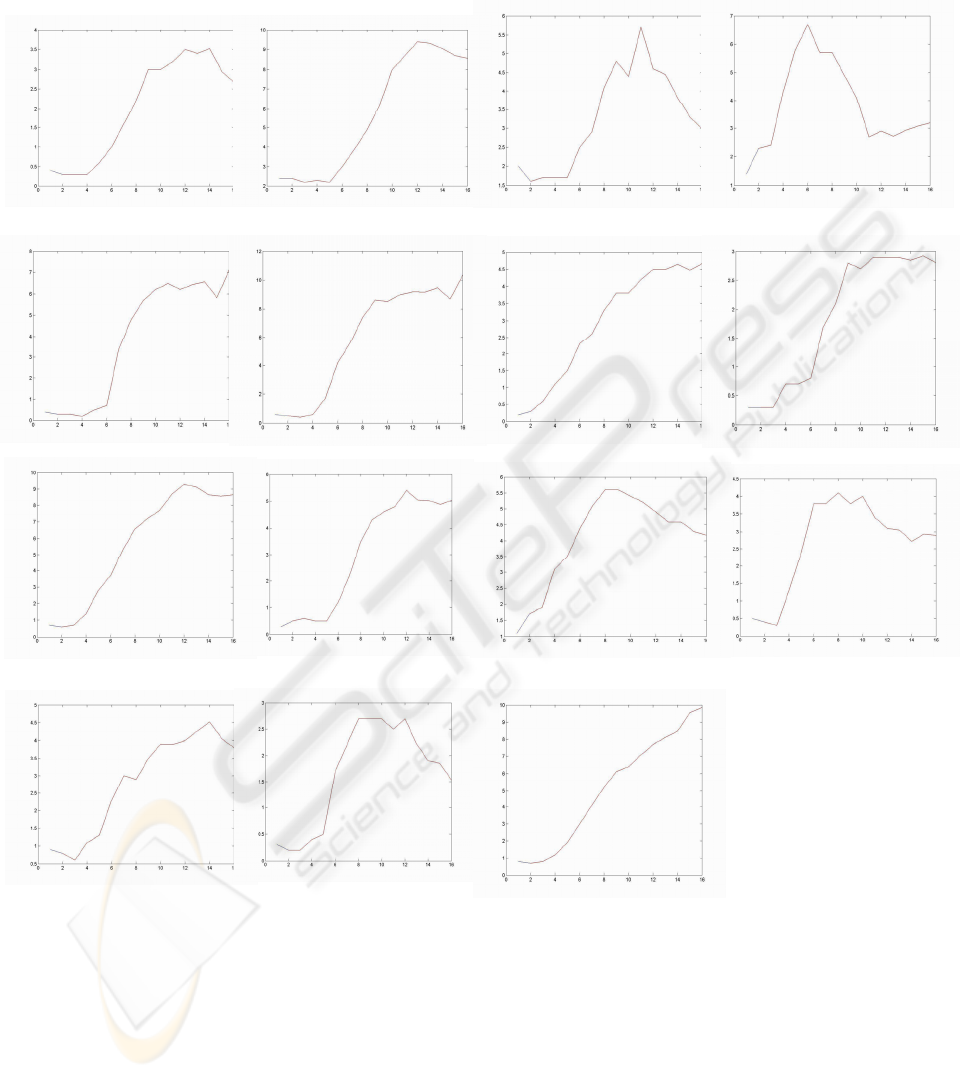
X represents the year of data and axis Y represents

the gross inner product.

The results obtained after of training can be

consulted in the following figures:

ure 8: Castilla-Leon

Figure 9: Cataluña

ure 6: Canarias

ure 7: Cantabria

Figure 12: Madrid

ure 10: Extremadura

ure 13: Castilla-Mancha

As we can observe the level the learning is very

high. In the following table (table 1) where we show

the MSE commited in the train, the values are very

low. Therefore, we realized a good approximation to

the functions.

ure 11: Galicia

Figure 2: Andalucia Figure 3: Aragón

Figure 14: Murcia

Figure 15: Rioja

ure 4: Asturias Fi

ure 5: Baleares

ure 16: Valencia

AN ADAPTABLE TIME-DELAY NEURAL NETWORK TO PREDICT THE SPANISH ECONOMIC INDEBTEDNESS

459

Table 1: The midle MSE of ten ejecution the

algorithm over Time-Delay Neural Network

COMMUNITY Medium Square Error

Andalucía 9.12219e-025

Aragón 3.40256e-023

Asturias 1.76825e-023

Baleares 2.27909e-024

Islas Canarias 9.21784e-023

Cantabria 4.14689e-027

Castilla León 3.61551e-024

Cataluña 1.86823e-022

Extremadura 1.88568e-023

Galicia 1.2120e-022

Madrid 1.32362e-022

Castilla-La Mancha 9.95153e-024

Murcia 1.97685e-023

Rioja 4.97758e-026

Valencia 1.84428e-023

The following table (table 2) shows the inference

for 2001 year:

COMMUNITY RATE OF INDEBTEDNESS

Andalucía 8.741354

Aragón 5.114635

Asturias 2.888294

Baleares 1.498553

Islas Canarias 2.266441

Cantabria 3.356926

Castilla León 3.237302

Cataluña 8.366449

Extremadura 7.838027

Galicia 10.958742

Madrid 4.669944

Castilla-La Mancha 2.814105

Murcia 4.371530

Rioja 2.810956

Valencia 10.338479

5 CONCLUSIONS

In this paper, we show that the assignment MSE

committed is very low.

Therefore, we show how TDNN and Levenberg-

Marquardt act over the values of Spanish economic

indebtedness. The error commited is very low and

therefore the ajust is very good. The new

approximate with TDNN- Levenberg-Marquardt

give better result as other work with Finite Impulse

Response Neural Network (M.P. Cuellar et al.

2003). We obtain the best solution for time-series

predictions in case of indebtedness in comparison

with other neural network topology and studies.

REFERENCES

Cuellar, M.P., Navarro, M.A., Pegalajar, M.C., Pérez-

Pérez, R. 2003. A Fir Neural Network to model the

autonomous indebtedness. Proceedings of the X SIGEF

Congress, vol I. Leon. Pp. 199-209.

Cybenko G. 1989. Approximation by superpositions of a

sigmoidal function. Mathematics of Control, Signals,

and Systems, vol 2 no. 4.

Haykin, S. 1998. Neural Network: A Comprehensive

Foundation. Second Edition. Prentice Hall.

Hornik, K. Stinchombe M. and White H. 1989. Multilayer

feedforward networks are universal approximators.

Neural Networks, vol 2, pp. 359-366.

Irie B. and Miyake S. 1988. Capabilities of three-layered

perceptrons. Proceedings of the IEEE Second

International Conference on Neural Networks, vol I,

San Diego, CA, July 1988, pp.641-647.

Kanzow C., Yamashita, N. And Fukushima, M. 2002.

Levenberg-Marquardt methods for constrained

nonlinear equations with strong local convergence

properties.April 23

Lang, K.J., and G.E. Hinton, 1988. The development of

the time-delay neural network architecture for speech

recognition. Technical Report CMU-CS-88-152,

Carnegie-Mellon University, Pittsburgh, PA.

Marquardt, D.W. 1963. An algorithm for least-squares

estimation of nonlinear parameters. Journal of the

Society for industrial and Applied Mathematics,

11:431-441.

Mor, J.J. 1977. The Levenberg-Marquardt Algorithm:

Implementation and Theory, in Numerical Analysis, G.

A. Watson, ed., Lecture Notes in Mathematics, vol.

630, Springer-Verlag, Berlin, 1977, pp. 105-116.

Ricardo, B.C., Prudëncio and Teresa B. Ludermir. Neural

Network Hybrid Learning: Genetic Algoritms &

Levenberg-Marquardt.

Waibel, A., T. Hanazawa, G.Hinton, K.Shikano, and K.J.

Lang, 1989. Phoneme recognition using time-delay

neural networks. IEEE Transactions on Acoustics,

Speech, and Signal Processing, vol. ASSP-37, pp.328-

339.

Weigend, A. Huberman, B. and Rumelhart, D. 1990.

Predicting the future: a connectionist approach.

International Journal of Neural Systems, vol 7, no. 3-4,

pp. 403-430.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

460