
NEW ENERGETIC SELECTION PRINCIPLE
IN DIFFERENTIAL EVOLUTION
Vitaliy Feoktistov
Centre de Recherche LGI2P, Site EERIE, EMA
Parc Scientifique Georges Besse, 30035 Nimes, France
Stefan Janaqi
Centre de Recherche LGI2P, Site EERIE, EMA
Parc Scientifique Georges Besse, 30035 Nimes, France
Keywords:
differential evolution, evolutionary algorithms, heuristics, optimization, selection.
Abstract:
The Differential Evolution algorithm goes back to the class of Evolutionary Algorithms and inherits its phi-
losophy and concept. Possessing only three control parameters (size of population, differentiation and recom-
bination constants) Differential Evolution has promising characteristics of robustness and convergence. In
this paper we introduce a new principle of Energetic Selection. It consists in both decreasing the population
size and the computation efforts according to an energetic barrier function which depends on the number of
generation. The value of this function acts as an energetic filter, through which can pass only individuals with
lower fitness. Furthermore, this approach allows us to initialize the population of a sufficient (large) size. This
method leads us to an improvement of algorithm convergence.
1 INTRODUCTION
Evolutionary Algorithms increasingly become the
primary method of choice for optimization problems
that are too complex to be solved by deterministic
techniques. They are universal, robust, easy to use
and inherently parallel. The huge number of appli-
cations and continuous interest prove it during sev-
eral decades (Heitk
¨
otter and Beasley, 2000; Beasley,
1997). In comparison with the deterministic methods
Evolutionary Algorithm require superficial knowl-
edge about the problem being solved. Generally, the
algorithm only needs to evaluate the cost function for
a given set of input parameters. Nevertheless, in most
cases such heuristics take less time to find the opti-
mum than, for example, gradient methods. One of the
latest breakthroughs in the evolutionary computation
is the Differential Evolution algorithm.
2 DIFFERENTIAL EVOLUTION
Differential Evolution (DE) is a recently invented
global optimization technique (Storn and Price,
1995). It can be classified as an iterative stochas-
tic method. Enlarging the Evolutionary Algorithms’
group, DE turns out to be one of the best population-
based optimizers (Storn and Price, 1996; Feoktis-
tov and Janaqi, 2004c; Feoktistov and Janaqi, 2004a;
Feoktistov and Janaqi, 2004b). In the following lines
we give a brief description of DE algorithm.
An optimization problem is represented by a set of
variables. Let these variables form a D-dimensional
vector in continuous space X = (x
1
, . . . , x
D
) ∈
IR
D
. Let there be some criterion of optimization
f : IR
D
→ IR, usually named fitness or cost function.
Then the goal of optimization is to find the values of
the variables that minimize the criterion, i.e. to find
X
∗
: f(X
∗
) = min
X
f(X) (1)
Often, the variables satisfy boundary constraints
L ≤ X ≤ H : L, H ∈ IR
D
(2)
As all Evolutionary Algorithms, DE deals with a
population of solutions. The population IP of a gener-
ation g has NP vectors, so-called individuals of pop-
ulation. Each such individual represents a potential
optimal solution.
IP
g
= X
g
i
, i = 1, . . . , N P (3)
In turn, the individual contains D variables, so called
genes.
X
g
i
= x
g
i,j
, j = 1, . . . , D (4)
The population is initialized by randomly generat-
ing individuals within the boundary constraints,
IP
0
= x
0
i,j
= rand
i,j
· (h
j
− l
j
) + l
j
(5)
29
Feoktistov V. and Janaqi S. (2004).
NEW ENERGETIC SELECTION PRINCIPLE IN DIFFERENTIAL EVOLUTION.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 29-35
DOI: 10.5220/0002631200290035
Copyright
c
SciTePress

where rand function generates values uniformly in
the interval [0, 1].
Then, for each generation the individuals of the
population are updated by means of a reproduction
scheme. Thereto for each individual ind a set of other
individuals π is randomly extracted from the popula-
tion. To produce a new one the operations of Differ-
entiation and Recombination are applied one after an-
other. Next, the Selection is used to choose the best.
Now briefly consider these operations.
Here, we show the typical model of the Differenti-
ation, others can be found in (Feoktistov and Janaqi,
2004a; Feoktistov and Janaqi, 2004c). For that, three
different individuals π = {ξ
1
, ξ
2
, ξ
3
} are randomly
extracted from a population. So, the result, a trial in-
dividual, is
τ = ξ
3
+ F · (ξ
2
− ξ
1
) , (6)
where F > 0 is the constant of differentiation.
After, the trial individual τ is recombined with up-
dated one ind. The Recombination represents a typ-
ical case of a genes’ exchange. The trial one inherits
genes with some probability. Thus,
ω
j
=
½
τ
j
if rand
j
< Cr
ind
j
otherwise
(7)
where j = 1, . . . , D and Cr ∈ [0, 1) is the constant
of recombination.
The Selection is realized by comparing the cost
function values of updated and trial individuals. If
the trial individual better minimizes the cost function,
then it replaces the updated one.
ind =
½
ω if f(ω) ≤ f(ind)
ind otherwise
(8)
Notice that there are only three control parameters
in this algorithm. These are N P – population size, F
and Cr – constants of differentiation and recombina-
tion accordingly. As for the terminal conditions, one
can either fix the number of generations g
max
or a de-
sirable precision of a solution V T R (value to reach).
The pattern of DE algorithm is presented in Algo-
rithm 1.
3 DIFFERENTIATION
Differentiation occupies a quite important position in
the reproduction cycle. So, we try to analyze it in
detail.
Geometrically, Differentiation consists in two si-
multaneous operations: the first one is the choice of
a Differentiation’s direction and the second one is the
calculation of a step length in which this Differenti-
ation performs. From the optimization point of view
we have to answer the next two questions:
Algorithm 1 Differential Evolution
Require: F, Cr, N P – control parameters
initialize IP
0
← {ind
1
, . . . , ind
NP
}
evaluate f(IP
0
)
while (terminal condition) do
for all ind ∈ IP
g
do
IP
g
→ π = {ξ
1
, ξ
2
, . . . , ξ
n
}
τ ← Diff erentiate(π, F )
ω ← Recombine(τ, Cr)
ind ← Select(ω, ind)
end for
g ← g + 1
end while
1. How to choose the optimal direction from all avail-
able ones?
2. What step length is necessary in order to better
minimize the cost function along the chosen direc-
tion?
Let us remind that the principle of Differentiation
is based on a random extraction of several individuals
from the population and the geometrical manipulation
of them.
Possible directions of Differentiation entirely de-
pend on the disposition of extracted individuals. Also,
their disposition influences the step length. Further-
more by increasing either the size of population or
the number of extracted individuals we augment the
diversity of possible directions and the variety of step
lengths. Thereby we intensify the exploration of the
search space. But on the other hand, the probability
to find the best combination of extracted individuals
goes considerably down.
Example. We take the typical differentiation strat-
egy u = x
1
+ F · (x
2
− x
3
), where for each cur-
rent individual three other individuals are randomly
extracted from the population.
• In the first case we suppose that the population
consists only of four individuals. So there are
(4 − 1)(4 − 2)(4 − 3) = 3 · 2 · 1 = 6 possible di-
rections and 6 possible step lengths. Imagine then
that only one combination gives the best value of
the cost function. Therefore the probability to find
it, is 1/6.
• In the second case the population size is equal to
five individuals. It gives (5 − 1)(5 − 2)(5 − 3) =
4 · 3 · 2 = 24 directions and as many step lengths.
But, in this case, the probability to find the best
combination is much less – 1/24.
If we choose another strategy consisting of two ran-
domly extracted individuals, u = x
1
+ F · (x
2
− x
1
)
for example, then for the population size of five in-
dividuals the diversity of possible directions and step
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
30

lengths is equal now to (5−1)(5−2) = 12 (two times
less then in the previous case).
As we can see only two factors control the capa-
bility of the search space exploration. These are the
population size N P and the number of randomly ex-
tracted individuals k in the strategy. In the case of
the consecutive extraction of individuals the depen-
dence of the potential individuals diversity from both
the population size and the number of extracted indi-
viduals is shown in the Formula 9.
f(NP, k) =
k
Y
i=1
(NP − i) (9)
But, where is the compromise between the covering
of the search space (i.e. the diversity of directions and
step lengths) and the probability of the best choice?
This question makes us face with a dilemma that was
named ”The Dilemma of the search space exploration
and the probability of the optimal choice”.
During the evolutionary process the individuals
learn the cost function surface (Price, 2003). The step
length and the difference direction adapt themselves
accordingly. In practice, the more complex the cost
function is, the more exploration is needed. The bal-
anced choice of N P and k defines the efficiency of
the algorithm.
4 ENERGETIC APPROACH
We introduce a new energetic approach which can be
applied to population-based optimization algorithms
including DE. This approach may be associated with
the processes taking place in physics.
Let there be a population IP consisting of NP in-
dividuals. Let us define the potential of individual
as its cost function value ϕ = f(ind). Such poten-
tial shows the remoteness from the optimal solution
ϕ
∗
= f (ind
∗
), i.e. some energetic distance (poten-
tial) that should be overcome to reach the optimum.
Then, the population can be characterized by supe-
rior and inferior potentials ϕ
max
= max f (ind
i
) and
ϕ
min
= min f (ind
i
). As the population evolves the
individuals take more optimal energetic positions, the
closest possible to the optimum level. So if t → ∞
then ϕ
max
(t) → ϕ
min
(t) → ϕ
∗
, where t is an el-
ementary step of evolution. Approaching the opti-
mum, apart from stagnation cases, can be as well ex-
pressed by ϕ
max
→ ϕ
min
or (ϕ
max
− ϕ
min
) → 0.
By introducing the potential difference of population
4ϕ(t) = ϕ
max
(t) − ϕ
min
(t) the theoretical condi-
tion of optimality is represented as
4ϕ(t) → 0 (10)
In other words, the optimum is achieved when the po-
tential difference is closed to 0 or to some desired
precision ε. The value 4ϕ(t) is proportional to the
algorithmic efforts, which are necessary to find the
optimal solution.
Thus, the action A done by the algorithm in order
to pass from one state t
1
to another t
2
is
A(t
1
, t
2
) =
Z
t
2
t
1
4ϕ(t)dt (11)
We introduce then the potential energy of popula-
tion E
p
that describes total computational expenses.
E
p
=
Z
∞
0
4ϕ(t)dt (12)
Notice that the equation (12) graphically repre-
sents the area S
p
between two functions ϕ
max
(t) and
ϕ
min
(t).
Figure 1: Energetic approach.
Let us remind that our purpose is to increase the
speed of algorithm convergence. Logically, the con-
vergence is proportional to computational efforts. It is
obvious the less is potential energy E
p
the less com-
putational efforts are needed. Thus, by decreasing the
potential energy E
p
≡ S
p
we augment the conver-
gence rate of the algorithm. Hence, the convergence
increasing is transformed into a problem of potential
energy minimization (or S
p
minimization).
E
∗
p
= min
4ϕ(t)
E
p
(4ϕ(t)) (13)
5 NEW ENERGETIC SELECTION
PRINCIPLE
5.1 The Idea
We apply the above introduced Energetic Approach to
the DE algorithm. As an elementary evolution step t
we choose a generation g.
NEW ENERGETIC SELECTION PRINCIPLE IN DIFFERENTIAL EVOLUTION
31
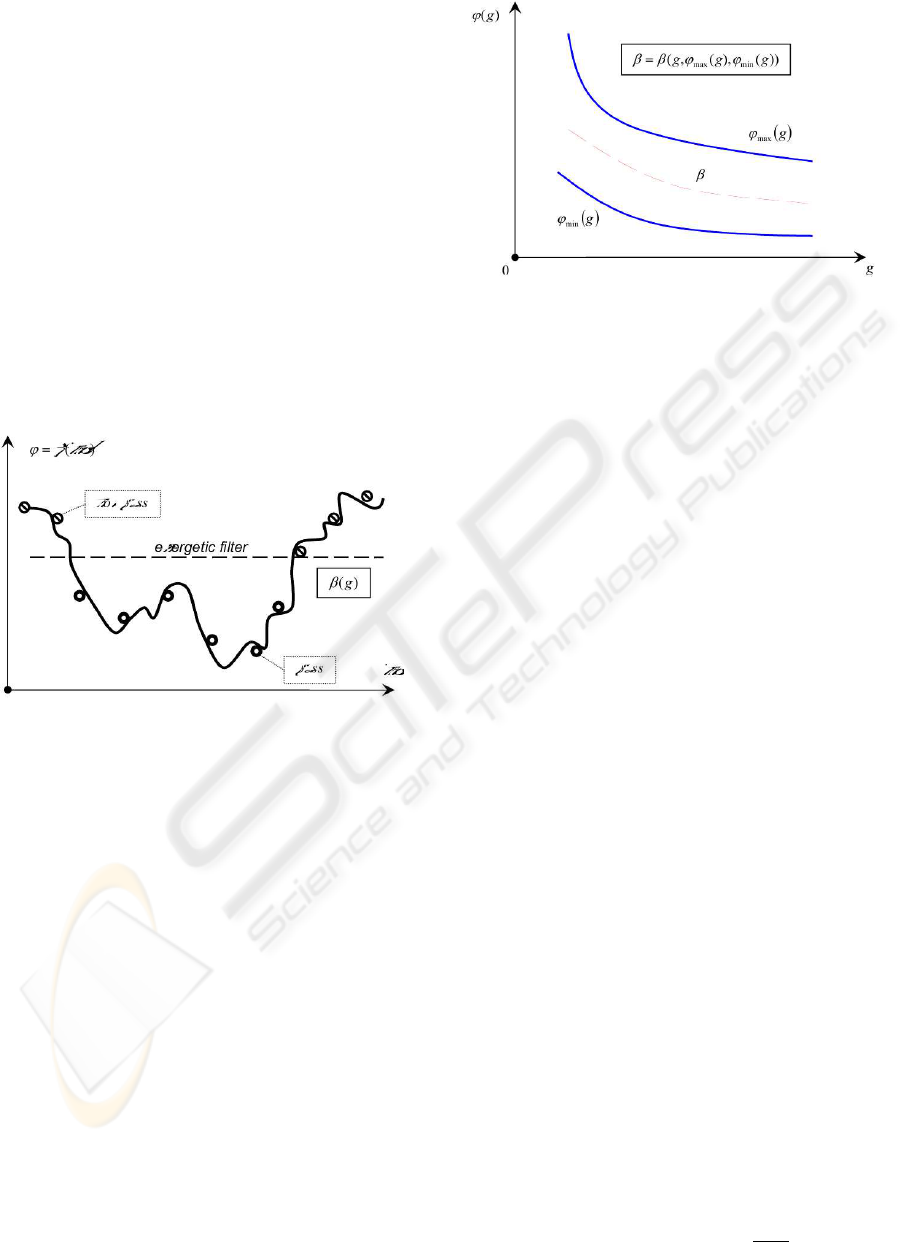
In order to increase the convergence rate we min-
imize the potential energy of population E
p
(Fig.1).
For that a supplementary procedure is introduced at
the end of each generation g. The main idea is to
replace the superior potential ϕ
max
(g) by so called
energetic barrier function β(g). Such function artifi-
cially underestimates the potential difference of gen-
eration 4ϕ(g).
β(g) − ϕ
min
(g) ≤ ϕ
max
(g) − ϕ
min
(g)
⇔ β(g) ≤ ϕ
max
(g), ∀g ∈ [1, g
max
]
(14)
From an algorithmic point of view this function
β(g) serves as an energetic filter for the individuals
passing into the next generation. Thus, only the indi-
viduals with potentials less than the current energetic
barrier value can participate in the next evolutionary
cycle (Fig.2).
Figure 2: Energetic filter.
Practically, it leads to the decrease of the popula-
tion size NP by rejecting individuals such that:
f(ind) > β(g) (15)
5.2 Energetic Barriers
Here, we show some examples of the energetic barrier
function. At the beginning we outline the variables
which this function should depend on. Firstly, this is
the generation variable g, which provides a passage
from one evolutionary cycle to the next. Secondly, it
should be the superior potential ϕ
max
(g) that presents
the upper bound of the barrier function. And thirdly,
it should be the inferior potential ϕ
min
(g) giving the
lower bound of the barrier function (Fig.3).
Linear energetic barriers. The simplest example
is the use of a proportional function. It is easy to ob-
tain by multiplying either ϕ
min
(g) or ϕ
max
(g) with
a constant K.
Figure 3: Energetic barrier function.
In the first case, the value ϕ
min
(g) is always stored
in the program as the current best value of the cost
function. So, the energetic barrier looks like
β
1
(g) = K · ϕ
min
(g), K > 1 (16)
The constant K is selected to satisfy the energetic bar-
rier condition (14).
In the second case, a little procedure is necessary to
find superior potential (maximal cost function value
of the population) ϕ
max
(g). Here, the energetic bar-
rier is
β
2
(g) = K · ϕ
max
(g), K < 1 (17)
K should not be too small in order to provide a
smooth decrease of the population size NP .
An advanced example would be a superposition of
the potentials.
β
3
(g) = K · ϕ
min
(g) + (1 − K) · ϕ
max
(g) (18)
So, with 0 < K < 1 the energetic barrier function is
always found between the potential functions. Now,
by adjusting K it is easier to get the smoothed re-
duction of the population without condition violation
(14). Examples of the energetic barrier functions are
shown on the figure (Fig.4).
Nonlinear energetic barriers. As we can see the
main difficulty of using the linear barriers appears
when we try to define correctly the barrier function in
order to provide a desired dynamics of the population
reduction. Taking into consideration that ϕ
max
→
ϕ
min
when the algorithm converges locally, the ideal
choice for the barrier function is a function which be-
gins at a certain value between ϕ
min
(0) and ϕ
max
(0)
and converges to ϕ
max
(g
max
).
Thereto, we propose an exponential function K(g)
K(g) = K
l
+ (K
h
− K
l
) · e
(
−
T
g
max
·g
)
(19)
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
32
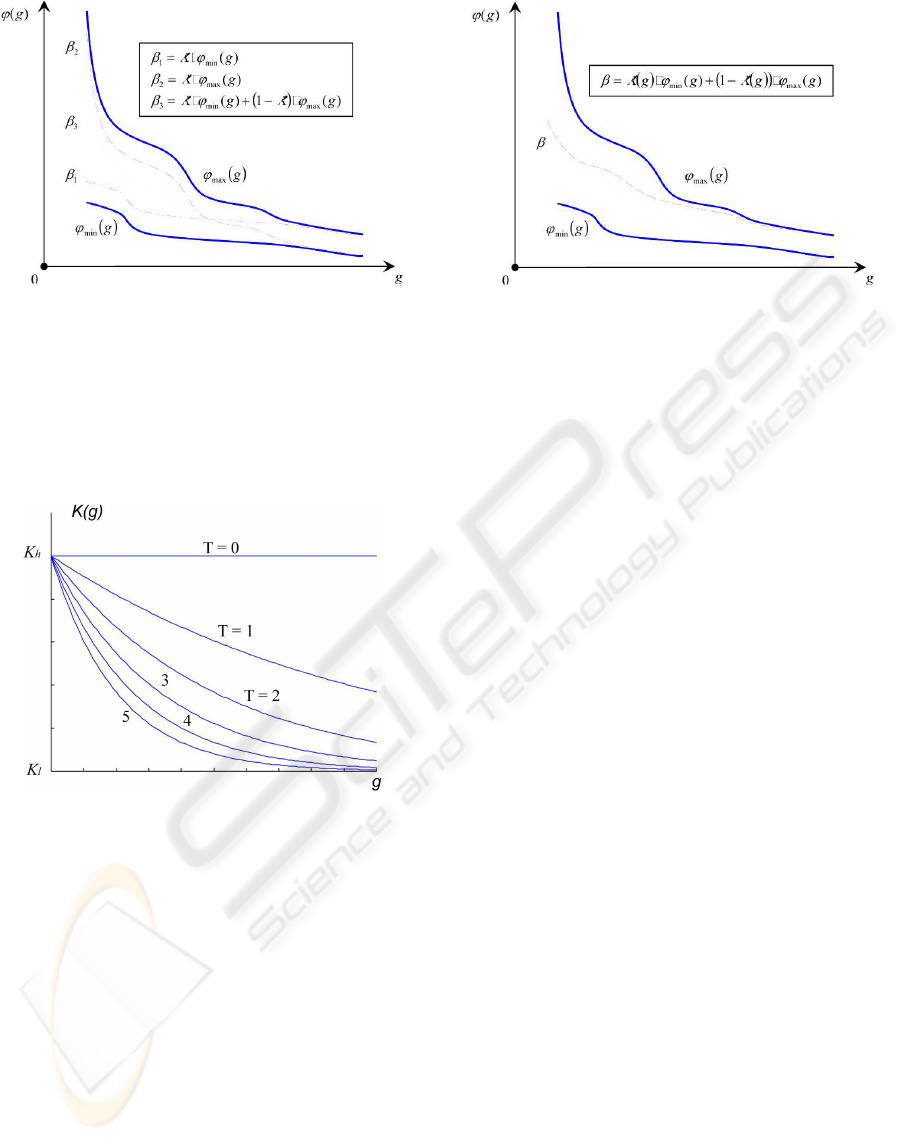
Figure 4: Linear energetic barriers.
This function, inspired by the color-temperature de-
pendence from Bernoulli’s low, smoothly converges
from K
h
to K
l
. The constant T , so called temper-
ature, controls the convergence rate. The functional
dependence on the temperature constant K(T ) is rep-
resented on the figure (Fig.5).
Figure 5: Exponential function K(g, T ).
By substituting the constant K in the equations (16-
18) for the exponential function (19) we can supply
the energetic barrier function with improved tuning
(Fig.6).
5.3 Advantages
Firstly, such principle of energetic selection permits
to initialize the population of a sufficiently large size.
This fact leads to better (careful) exploration of a
search space during the initial generations as well as
it increases the probability of finding the global opti-
mum.
Secondly, the introduction of the energetic barrier
function decreases the potential energy of the popula-
tion and thereby increases the algorithm rate.
Thirdly, a double selection principle is applied. The
first one is a usual DE selection for each individual
Figure 6: Nonlinear energetic barrier.
of a population. Here, there is no reduction of the
population size. And the second one is a selection of
the best individuals which pass in the next generation,
according to the energetic barrier function. It leads to
the reduction of the population size.
Remark. Notice that a considerable reduction of
the population size occurs at the beginning of the
evolutionary process. For more efficient exploitation
of this fact a population should be initialized with
greatly larger size N P
0
than usually. Then, when the
population shrinks to a certain size NP
f
, it is neces-
sary to stop the energetic selection procedure. This
forced stopping is explained by possible stagnation
and not enough efficient search in a small size pop-
ulation. In fact, the first group of generations locates
a set of promising zones. The selected individuals are
conserved in order to make a thorough local search in
these zones.
6 COMPARISON OF RESULTS
In order to test our approach we chose three test func-
tions (20) from a standard test suite for Evolutionary
Algorithms (Whitley et al., 1996). The first two
functions, Sphere f
1
and Rosenbrock’s function f
2
,
are classical De Jong testbads (Jong, 1975). Sphere
is a ”dream” of every optimization algorithm. It
is smooth, unimodal and symmetric function. The
performance on the Sphere function is a measure
of the general efficiency of the algorithm. Whereas
the Rosenbrock’s function is a nightmare. It has a
very narrow ridge. The tip of the ridge is very sharp
and it runs around a parabola. The third function,
Rotated Ellipsoid f
3
, is a true quadratic non separable
optimization problem.
NEW ENERGETIC SELECTION PRINCIPLE IN DIFFERENTIAL EVOLUTION
33

f
1
(X) =
3
X
i=1
x
2
i
f
2
(X) = 100(x
2
1
− x
2
)
2
+ (1 − x
1
)
2
f
3
(X) =
20
X
i=1
i
X
j=1
x
j
2
(20)
We fixed the differentiation F and recombination
Cr constants to be the same for all functions. F =
0.5. Recombination Cr = 0 (there is no recombina-
tion) in order to make the DE algorithm rotationally
invariant (Salomon, 1996; Price, 2003). The terminal
condition of algorithm is a desirable precision of op-
timal solution V T R (value to reach). It is fixed for
all tests as V T R = 10
−6
. We count the number of
function evaluations NF E needed to reach the V T R.
The initial data are shown in the Table 6.
Table 1: Initial test data.
f
i
D NP NP
0
NP
f
K
1 3 30 90 25 0.50
2 2 40 120 28 0.75
3 20 200 600 176 0.15
For DE with energetic selection principle the ini-
tial population size was chosen three times larger than
in the classical DE scheme: N P
0
= 3 · NP . The
forced stopping was applied if the current population
became smaller than NP . Hence NP
f
≤ NP . As
an energetic barrier function the linear barrier β
3
(g)
was selected (18). So, K is an adjusting parameter
for barrier tuning, which was found empirically. D is
the dimension of the test functions.
The average results of 10 runs for both the classical
DE scheme and DE with energetic selection principle
are summarized in the Table 2.
Table 2: Comparison the classical DE scheme (cl) and DE
with energetic selection principle (es).
f
i
NF E
cl
NF E
es
δ, %
1 1088.7 912.4 16,19
2 1072.9 915.3 14,69
3 106459.8 94955.6 10,81
The numbers of function evaluations (NF E’s)
were compared. It is considered that NF E
cl
value
is equal to 100% therefore the relative convergence
amelioration in percentage wise can be defined as
δ = 1 −
NF E
es
NF E
cl
(21)
Thus, δ may be interpreted as the algorithm improve-
ment.
Remark. We tested DE with a great range of other
functions. The stability of results was observed. So,
in order to demonstrate our contribution we have gen-
erated only 10 populations for each test function rely-
ing on the statistical correctness. Nevertheless farther
theoretical work and tests are necessary.
7 CONCLUSION
The variation of the population size of population-
based search procedures presents a rather promising
trend. In this article we have examined its decrease.
The proposed energetic approach explains a theoret-
ical aspect of such population reduction. The effi-
ciency of the new energetic selection principle based
on this energetic approach is illustrated by the exam-
ple of the DE algorithm. The given innovation pro-
vides more careful exploration of a search space and
leads to the convergence rate improvement. Thus,
the probability of the global optimum finding is in-
creased. Further works are carried on the methods of
increasing the population size.
REFERENCES
Beasley, D. (1997). Possible applications of evolution-
ary computation. In B
¨
ack, T., Fogel, D. B., and
Michalewicz, Z., editors, Handbook of Evolutionary
Computation, pages A1.2:1–10. IOP Publishing Ltd.
and Oxford University Press, Bristol, New York.
Feoktistov, V. and Janaqi, S. (2004a). Generalization of the
strategies in differential evolutions. In 18th Annual
IEEE International Parallel and Distributed Process-
ing Symposium. IPDPS – NIDISC 2004 workshop,
page (accepted), Santa Fe, New Mexico – USA. IEEE
Computer Society.
Feoktistov, V. and Janaqi, S. (2004b). Hybridization of
differential evolution with least-square support vec-
tor machines. In Proceedings of the Annual Machine
Learning Conference of Belgium and The Nether-
lands. BENELEARN 2004., pages 53–57, Vrije Uni-
versiteit Brussels, Belgium.
Feoktistov, V. and Janaqi, S. (2004c). New strategies in dif-
ferential evolution. In Parmee, I., editor, 6-th Interna-
tional Conference on Adaptive Computing in Design
and Manufacture, ACDM 2004, page (accepted), Bris-
tol, UK. Engineers House, Clifton, Springer-Verlag
Ltd.(London).
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
34

Heitk
¨
otter, J. and Beasley, D. (2000). Hitch Hiker’s Guide
to Evolutionary Computation: A List of Frequently
Asked Questions (FAQ).
Jong, K. A. D. (1975). An analysis of the behavior of a class
of genetic adaptive systems. PhD thesis, University of
Michigan.
Price, K. (2003). New Ideas in Optimization, Part 2: Dif-
ferential Evolution. McGraw-Hill, London, UK.
Salomon, R. (1996). Re-evaluating genetic algorithm per-
formance under coordinate rotation of benchmark
functions: A survey of some theoretical and practical
aspects of genetic algorithms. BioSystems, 39:263–
278.
Storn, R. and Price, K. (1995). Differential evolution - a
simple and efficient adaptive scheme for global opti-
mization over continuous spaces. Technical Report
TR-95-012, International Computer Science Institute,
Berkeley, CA.
Storn, R. and Price, K. (1996). Minimizing the real func-
tions of the ICEC’96 contest by differential evolu-
tion. In IEEE International Conference on Evolu-
tionary Computation, pages 842–844, Nagoya. IEEE,
New York, NY, USA.
Whitley, D., Rana, S. B., Dzubera, J., and Mathias, K. E.
(1996). Evaluating evolutionary algorithms. Artificial
Intelligence, 85(1-2):245–276.
NEW ENERGETIC SELECTION PRINCIPLE IN DIFFERENTIAL EVOLUTION
35
