LEARNING BAYESIAN NETWORKS WITH LARGEST CHAIN

GRAPHS

Mohamed BENDOU

ESIEA Recherche

38 rue des Docteurs Calmette et Gu

erin

53 000 Laval, France

Paul MUNTEANU

ESIEA Recherche

Keywords:

Bayesian networks, equivalence classes, learning, largest chain graphs, essential graphs, instanciable partially

oriented graph

Abstract:

This paper proposes a new approach for designing learning bayesian network algorithms that explore the

structure equivalence classes space. Its main originality consists in the representation of equivalence classes

by largest chain graphs, instead of essential graphs which are generally used in the similar task. We show

that this approach drastically simpliﬁes the algorithms formulation and has some beneﬁcial aspects on their

execution time.

1 INTRODUCTION

Learning Bayesian networks from data is one of the

most ambitious approaches to Knowledge Discovery

in Databases. Unlike most other data mining tech-

niques, it does not focus its search on a particular kind

of knowledge but aims at ﬁnding all the (probabilis-

tic) relations which hold between the considered vari-

ables.

From a statistical viewpoint, a Bayesian network

efﬁciently encodes the joint probability distribution of

the variables describing an application domain. This

kind of knowledge allows making rational decisions

involving any arbitrary subset of these variables on

the basis of the available knowledge about another ar-

bitrary subset of variables.

Moreover, Bayesian networks may be represented

in a graphical annotated form which seems quite nat-

ural to human experts for a large variety of applica-

tions. The nodes of a Bayesian network correspond

to domain variables and the edges which connect the

nodes correspond to direct probabilistic relations be-

tween these variables. Under certain assumptions

(Spirtes et al., 1993), these relations have causal se-

mantics (a directed edge A → B may be interpreted

as A is a direct cause of B), while most other data

mining approaches deal exclusively with correlation.

There are two main approaches to learning

Bayesian networks with unknown structure. The

ﬁrst one is to build the network according to the

conditional independence relations found in data

(e.g., (Spirtes et al., 1993)). Traditionally, these

methods aim at discovering causal relations between

the variables and, therefore, emphasize the structural

ﬁdelity of the Bayesian networks they learn. How-

ever, they suffer from the lack of reliability of high-

dimensional conditional independence tests.

The other approach to learning Bayesian networks

is to deﬁne an evaluation function (or score) which

accounts for the quality of candidate networks with

respect to the available data and to use some kind of

search algorithm in order to ﬁnd, in a “reasonable”

amount of time, a network with an “acceptable” score

(we use the terms “reasonable” and “acceptable” be-

cause this learning task has been proven to be NP-

hard for the evaluation functions mentioned in the fol-

lowing section). These algorithms are less sensitive to

the quality of the available data and their results can

be successfully used in various decision making tasks.

However, as we have show in (Munteanu and Ben-

dou, 2001), there are many local optima in the space

of Bayesian networks and heuristic search algorithms

may easily be trapped in one of them. The explo-

ration of the space of Bayesian network structures by

a greedy search algorithm may end with a structure

which fails to reveal some independence relations be-

tween the variables and, therefore, may be rather dif-

ferent from the true one. The main reason for this is

the equality of the score of equivalent networks.

The space of equivalence classes of Bayesian net-

184

BENDOU M. and MUNTEANU P. (2004).

LEARNING BAYESIAN NETWORKS WITH LARGEST CHAIN GRAPHS.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 184-190

DOI: 10.5220/0002636301840190

 SciTePress

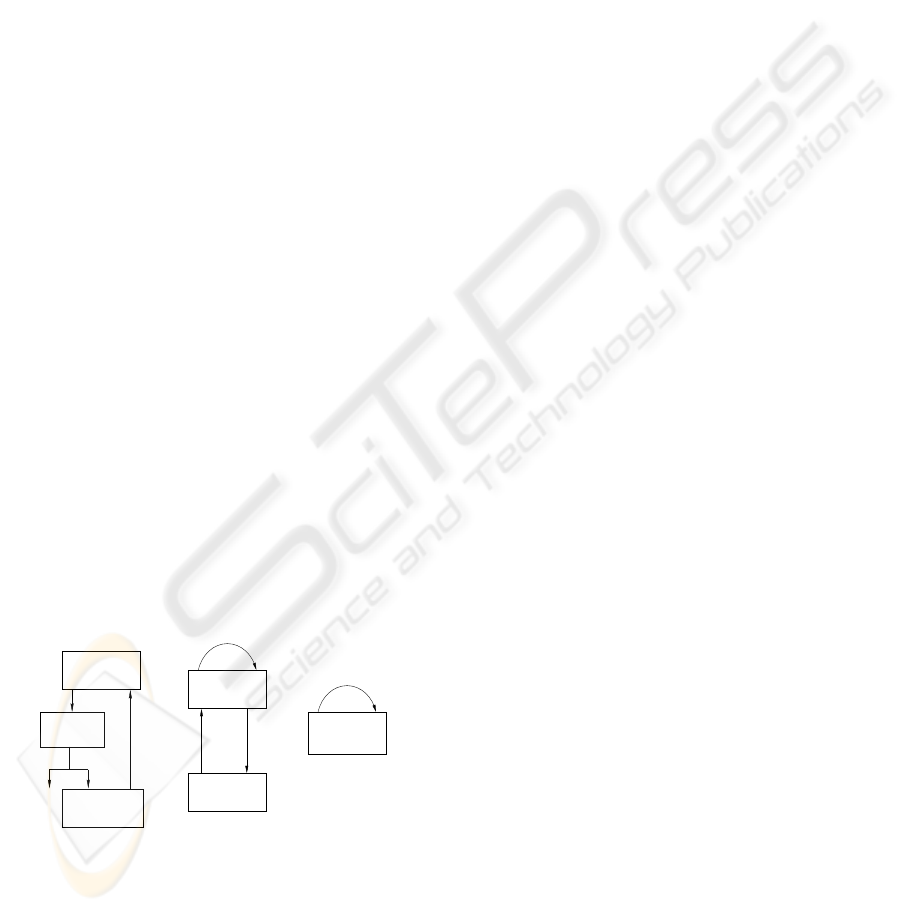
work structures seems to be better suited for this kind

of search. Learning algorithms which explore this

space have already been studied in (Chickering, 1996)

(ﬁg 1.a). Intuitively, this approach consists in allow-

ing the addition of undirected edges when no direc-

tion is preferred by the score. The conclusion of

this work was that the search in the space of equiva-

lence classes generally provides better results than the

search in the space of Bayesian networks but, unfor-

tunately, unfortunately, this algorithm is considerably

slower than classical ones. Mainly because they have

to build instances of the equivalence classes in order

to check their consistency and in order to calculate

their score.

In (Munteanu and Bendou, 2001) and (Bendou and

Munteanu, 2002) we have proposed an equivalence

classes leaning model EQ, as described in ﬁg 1.b. It

introduces the ”instantiable” partially oriented graphs

notion, provides the means for the veriﬁcation of the

consistency of these partially directed graphs and for

the computation of their score without instantiation.

In EQ, the transformation operators are constrained

to make sure that the transformed graphs are instan-

tiable. When the best instantiable partially oriented

graph is obtained, for each leaning step, it is trans-

formed on essential graphs. This approach consider-

ably reduces the execution time of the leaning task

in the space of equivalence classes. It became com-

parable to the execution time of the classical algo-

rithms that explore bayesian network structures space

for best result in terms of obtained precision results.

The price to pay for this efﬁciency is the concep-

tual complexity of the algorithms. In fact, they not

only require the development of the speciﬁc applica-

tion constraints for each transformation operation, but

they also require the non-trivial post-treatments to ob-

tain the essential graph result.

Best transformation

Transformation

Score

Calculating

graphs

Best transformation

Essential graphs

Partialy oriented

Constraints

Generation of

essential graph

a . Chickering model

c. EQ-LCG model

b. EQ model

Failure

Transformation

without constraints

Instances

generation

Success

Largest chain

Essential graph

Partially oriented

graphs

DAGs

Figure 1: Equivalence classes learning models

In this paper, we propose a new model for lean-

ing equivalence classes, EQ-LCG (EQ for equiva-

lence classes and LCG for largest chain graphs, see

ﬁg 1.c). The main originality of this model consists

in the representation of equivalence classes by largest

chain graphs (Frydenberg, 1990), instead the essential

graphs. As shown in ﬁg1, the using of largest chain

graphs allow to reduce the representation forms used

in the learning, with beneﬁcial effects on the concep-

tual complexity and on the EQ-LCG algorithms efﬁ-

ciency. EQ-LCG use one kind of graphs to represent

the structure classes evaluated in the learning and use

one algorithm (described in section 3.2) to validate all

the transformation operators

The next section introduces the theoretical notions

on which EQ-LCG is based. The EQ-LCG algorithm

aspects are presented in the section 3 and its experi-

ential evaluation make the object of the section 4.

2 THEORETICAL FRAMEWORK

Deﬁnition 1 (Equivalence) Two DAGs are equiva-

lent if and only if they represent the same conditional

independence relationships. A maximal set of equiva-

lent DAGs forms an equivalence class.

Verma and perl (Verma and Pearl, 1990) have charac-

terized the equivalence of the DAGs in term of struc-

ture:

Theorem 1 ((Verma and Pearl, 1990)) All Bayesian

networks belonging to the same equivalence class

have the same skeleton and the same v-structures

(Verma and Pearl, 1990).

A skeleton is an undirected graph resulting from

ignoring the directionality of edges and a v-structures

is triples of nodes A, B, C such that A and B are not

adjacent and are connected to C by the edges A →

C ← B.

Deﬁnition 2 (Instance) A DAG D is instance of an

arbitrary partially directed graph G if and only if :

• D and G have the same skeleton and the same v-

structures;

• D contain all the directed edges of G.

Deﬁnition 3 (Instantiable partially oriented graph)

A partially oriented graph is instantiable if and only

if it contains at less one instance.

The following deﬁnitions provide the rules for ori-

enting undirected edges (pseudo directed edges and

pseudo directed paths) and characterize the substruc-

tures of a partially directed graph that cannot be

instantiated (minimal undirected cycles, pseudo di-

rected cycles and colliding minimal chains).

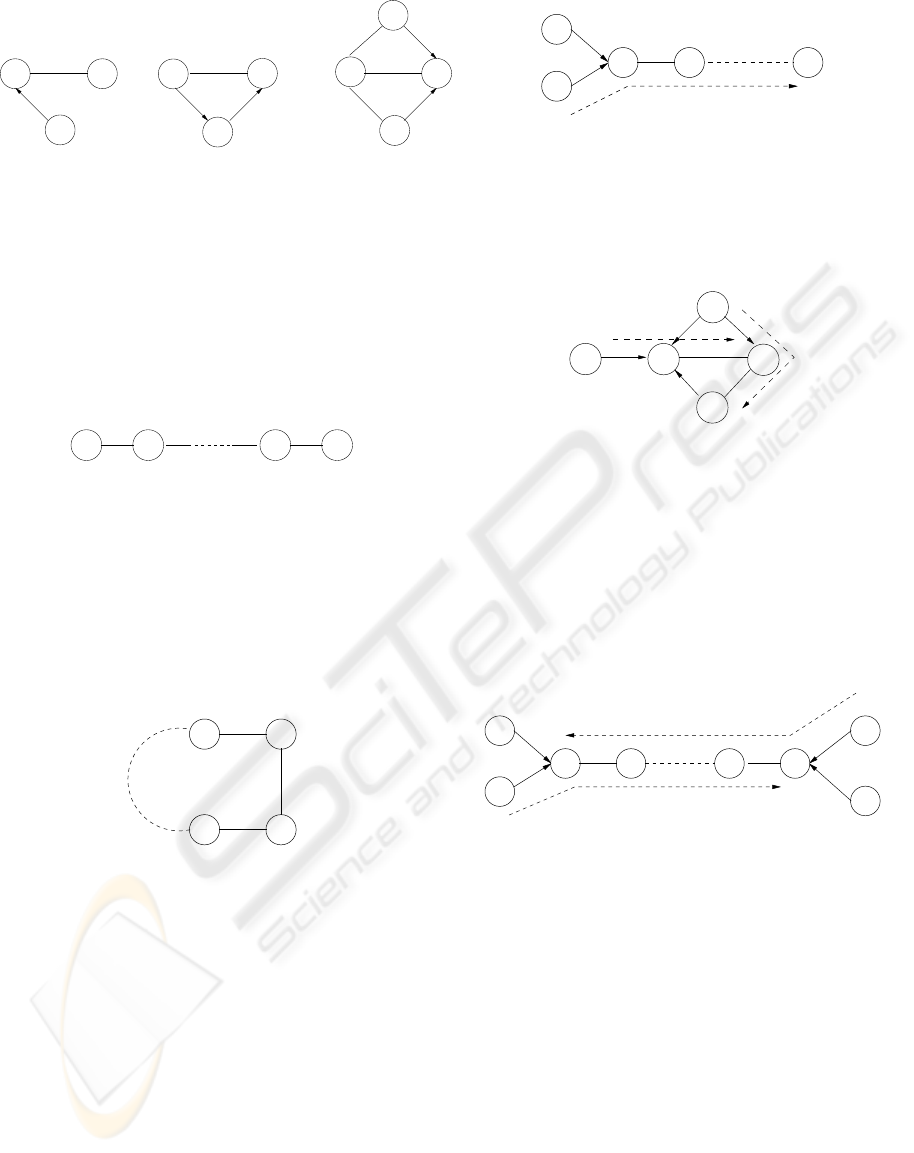
Deﬁnition 4 (Pseudo directed edges) We say that

an undirected edge X − Y of a graph G is a pseudo

directed edge from X to Y , and we note X

→

− Y , if

X − Y occurs in at least one of the three conﬁgura-

tions of ﬁg.2 as an induced subgraph of G.

LEARNING BAYESIAN NETWORKS WITH LARGEST CHAIN GRAPHS

185

Figure 2: Possible conﬁgurations for pseudo directed edges

The orientation of pseudo directed edges is directly

imposed by the neighboring directed edges in order to

prevent directed cycles or spurious v-structures.

Deﬁnition 5 (Minimal chain) A succession of undi-

rected edges X

, . . . , X

is called a minimal chain if

, X

i+2

are not adjacent for any i ≤ N − 2.

X2X1 XnXn-1

Figure 3: Minimal chain

All edges belonging to the same minimal chain

have to be oriented in the same direction in order to

avoid the introduction of spurious v-structures.

Deﬁnition 6 (Minimal undirected cycle) A minimal

chain X

, . . . , X

is called a minimal undirected cy-

cle if X

N −1

= X

and X

= X

Xi+3 Xi+2

Xi+1

Figure 4: Minimal undirected cycle

Alternatively, an undirected cycle is minimal if it is

not chordal (chords may be directed). Since all edges

of a minimal undirected cycle have to be oriented in

the same direction, this kind of substructure cannot be

instantiated.

Deﬁnition 7 (Pseudo directed path) We say that a

minimal chain X

, . . . , X

is a pseudo directed path,

and we note X

→

. . ., X

if X

→

− X

The orientation of the pseudo directed edges have

to be propagated through the graph along the pseudo

directed paths.

Deﬁnition 8 (Pseudo directed cycle) A partially di-

rected cycle is called a pseudo directed cycle if all

the undirected edges of the cycle belong to pseudo

X1 X2 Xn

Figure 5: Pseudo directed path

directed paths oriented in the same direction as the

cycle.

Figure 6: Example of a pseudo directed cycle

Since all its undirected edges have to be oriented in

the same direction, a pseudo directed cycle cannot be

instantiated.

Deﬁnition 9 (Colliding minimal chain) A minimal

chain X

, . . . , X

is called a colliding minimal chain

if and only if X

→

. . ., X

and X

←

. . . X

Xn−1X2

Figure 7: Colliding minimal chain

This kind of substructure cannot be instantiated

without introducing spurious v-structures.

The following quasi algorithmic theorem charac-

terizes instantiable graphs.

Theorem 2 A partially oriented graph, G, is instan-

tiable if and only if :

1. G does not contain any directed cycle;

2. G does not contain any pseudo directed cycle;

3. G does not contain any minimal undirected cycle;

4. G does not contain any colliding minimal chain.

It is obvious that the instances of an instantiable par-

tially oriented graphs are equivalent. So, the instan-

tiable partially oriented graphs generally represent

subsets of structures that belong to the same equiva-

lence classes and some instantiable partially oriented

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

186

graphs can represent all the equivalence classes. In

fact, all the equivalence classes can be represented by

at least one instantiable partially oriented graph and

most of the equivalence classes can be represented by

several distinct instantiable partially oriented graphs.

In order to realize a bijection between the equiv-

alence classes and the instantiable partially oriented

graphs that represent them, some privileged represen-

tatives have been chosen. Two approaches are gener-

ally used:

1. A ” maximal ” representation for the directed

edges (and ”minimal ” representation for undi-

rected edges : the essential graphs

2. A ” maximal ” representation for the undirected

edges (and ”minimal ” representation for directed

edges : the largest chain

graphs

Deﬁnition 10 (Essential Graph EG) the essential

graph represented one equivalence class is a partially

oriented graph in which :

• edges that may appear in either direction in net-

works belonging to the same equivalence class are

represented as undirected edges;

• the other edges are represented as directed edges.

Deﬁnition 11 (Largest Chain Graph LCG) The

largest chain graph represented one equivalence

class is a partially oriented graph in which :

• each directed edge belonging to v-structures of the

DAGS that forms teh equivalence class is repre-

sented as a directed edge.

• the other edges are represented as undirected

edges.

We can immediately notice the intuitive charac-

ter of this second representation choice in contrast

with the ﬁrst one. Indeed, it directly relies on the

equivalence classes characterization of Verma and

Pearl(theorem 1) : it sufﬁces to indicate by directed

edges the v-structures and by undirected edges the re-

maining of the DAGs skeleton belonging to the equiv-

alence class.

The ﬁgure 8 illustrates the example of an instan-

tiable partially oriented graph (it exists at less one ori-

entation that doesn’t introduce a news v-structure or

directed cycle). The graph b is an example of an es-

sential graph (all the undirected edges can be oriented

in the two direction and, if any directed edge is ori-

ented in the reverses direction, alors it destroys or in-

troduces v-structures). The graph c, contains four di-

rected edges that form a v structure, is a largest chain

graph.

A chain graph is a partially oriented graph that does not

contain any directed cycle or any partially directed cycle.

We take this appellation for the historic reason, although the

chain graph concept (more restraining than the instantiable

partially oriented graph concept) is not used directly in this

paper

cba

Figure 8: Examples of intantiable partially oriented graph,

essential graph and largest chain graph

3 ALGORITHMIC ASPECTS OF

EQ-LCG

3.1 Global algorithmic structure

EQ-LCG basically uses the same strategy than EQ, as

presented in (Munteanu and Bendou, 2001). It uses

the exploration of the equivalence classes of bayesian

networks, by using evaluation function that gives the

same score for the equivalence structures (it is the

case for most modern evaluation functions ).

Since the largest chain graphs are instantiable par-

tially oriented graphs, the evaluation methods for the

transformation operators developed in the EQ frame-

work (based on ﬁctional instanciations of the instan-

tiable partially oriented graph candidates) remains

also true. As shown in (Munteanu and Bendou,

2001), the natural transformation operations (addi-

tion/suppression of directed and undirected edge, ad-

dition of v-structure), can be evaluated in an eco-

nomic manner by calculating a reduced number of lo-

cal scores.

In algorithmic terms, the ﬁrst EQ-LCG advantage

against EQ is the use of the chain graph that consider-

ably simpliﬁes the post-treatments applied after each

transformation operation (see section 3.3).

Another important difference between EQ-LCG

and EQ are the constraints of transformation opera-

tions applicability. In EQ, we took a part of a theo-

ritical analysis (relatively complex) of each transfor-

mation operation in order to elaborate this applicabil-

ity constraints under declarative form. Even though

most of the c onstraints have a local expression that

make their veriﬁcation very efﬁcient, the constraint of

the absence of a directed cycle, often implies a global

analysis of the graph structure, is responsible of an

important part in the execution time. For this rea-

son, we decided to use in EQ-LCG, an algorithmic

approach, direct generalization of those used for the

veriﬁcation of the circuit absence, that has the merit

to apply in a homogeneous manner to all considered

transformation operations. The details of this algo-

LEARNING BAYESIAN NETWORKS WITH LARGEST CHAIN GRAPHS

187

rithm, that veriﬁes the applicability of a transforma-

tion operation by detecting the possible non instan-

tiable structures introduced by it, are presented in the

following section.

3.2 Instantiable structures detection

algorithm

The non-instantiable structure detection algorithm,

proposed here, is based on the characterization of the

partially oriented graphs previously presented. The

algorithm is called on two nodes that are implied in

the transformation operation candidate. It browses the

nodes of the network that are susceptible to belong to

non-instantiable substructure. The recursive calls are

directly imposed by the rules for orienting undirected

edges of the substructures proposed in section 2. Each

visited node is marked. If the same node is visited two

times, then the graph contains non-instantiable struc-

tures. The NextInStructure method has as input

two nodes : A and B. The node B is the current node

and the node A is the last visited node.

Algorithm 1 (”Instantiable structure detection (X,Y)”)

Begin

Mark the node X;

If NextInStructure (Y, X) then

The structure is not instantiable and end

Else the structure is instanciable

End

Algorithm 2 (”NextInStructure (B, A)”)

Begin

If (B is marked) then

Retour true

Mark the node B;

For each node ch child of B do

If NextInStructure(ch,B) then

The structure is not instantiable and end

For each node ch neighbor of B Do

If ch and A are disconnected then

If NextInStructure(ch,B) then

The structure is not instantiable and end

Else

If B - CH is pseudo directed edge then

If NextInStructure(ch,B) then

The structure is not instantiable

and end

Unmark then node B;

End

3.3 An application example : the

EQ-LCG3 algorithm

To ease the experimental evaluation of this theoriti-

cal and algorithmic framework, and its comparison to

EQ, we implemented an algorithm of EQ-LCG having

the same exploration method than EQ3 (Munteanu

and Bendou, 2001) in the space of equivalence classes

that will be called EQ-LCG 3.

EQ-LCG 3 uses the heuristic search method, which

explores the space largest chain graph by applying

greedy manner for the ﬁve transformation operators

deﬁned as follows:

Let G be the current largest chain graph and G

the

transformed graph. Remember G

has to be largest

chain graph and the transformation has to be tiny.

The following subsections present ﬁve operators

which respect these conditions. In order to improve

the efﬁciency of the search algorithm we consider

here two different operators for the addition of di-

rected and undirected edges.

3.3.1 Operator 1: Addition of a directed edge

Deﬁnition

= Op1(G, X, Y ) = G ∪ {X → Y }

Constraints We will consider the application of this

operator only when G’ is an instatiable graph (then we

call ”Instantiable structure detection algorithm form

X to Y )

post-treatment when the directed edges X → Y

and Y → X produce the same greatest improvement

of the score, the undirected edge X − Y is added.

3.3.2 Operator 2: Addition of an undirected

edge

Deﬁnition

= Op2(G, X, Y ) = G ∪ {X − Y }

Constraints There is not constraints. This opera-

tor is applied when the addition of the directed edges

X → Y and Y → X are possible and produce the

same greatest improvement of the score.

Post-treatment The superﬂuous v-structures are

disoriented.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

188

3.4 Operator 3: Addition of

v-structure

Deﬁnition

= Op3(G, X, Y, Z) =

(G \ {Y − Z}) ∪ {X → Y } ∪ {Y ← Z}

This operator realizes the addition of a directed

edge together with the orientation of a previously

undirected edge.

Constraints We will consider the application of this

operator only when G

is an instatiable graph (then we

call ”Instantiable structure detection algorithm form

X to Y )

Post-treatment : nothing

3.5 Operator 4: Suppression

undirected edge

Deﬁnition

= Op4(G, X, Y ) = G \ {X − Y }

Constraints We will consider the application of this

operator only when G

is an instatiable graph (then we

call ”Instantiable structure detection algorithm form

X to Y )

Post-treatment : nothing

3.6 Operator 5: Suppression of

directed

Deﬁnition

= Op4(G, X, Y ) = G \ X → Y

Constraints We will consider the application of this

operator only when G

is an instatiable graph (then we

call ”Instantiable structure detection algorithm form

X to Y )

Post-treatment : All the superﬂuous v-structures in

Y are disoriented.

4 EXPERIMENTAL RESULTS

In order to evaluate the LCG algorithm perfor-

mances, we have compared it experimentally to clas-

sical greedy search and tabu search in the space of

Bayesian networks.

Tabu search uses a tabu list of 10 states and stops

after 10 consecutive iterations without score improve-

ment. All algorithms use the MDL score, as deﬁned

in (Friedman and Goldszmidt, 1996).

The comparison has been realized on learning tasks

involving seven publicly available Bayesian networks

of various sizes: Cancer (1): 5 nodes, 5 edges, Asia

(2): 8 nodes, 8 edges, CarStarts (3): 18 nodes, 17

edges, Alarm (4): 37 nodes, 46 edges, and Hailﬁnder

(5): 56 nodes, 66 edges.

In order to improve the statistical signiﬁcance of

the experimental results, we have compared the algo-

rithms on thirty different data sets for each network

(1,000 examples for the small networks Cancer, Asia,

and 10,000 for the others, generated according to the

probability distributions modeled by the networks).

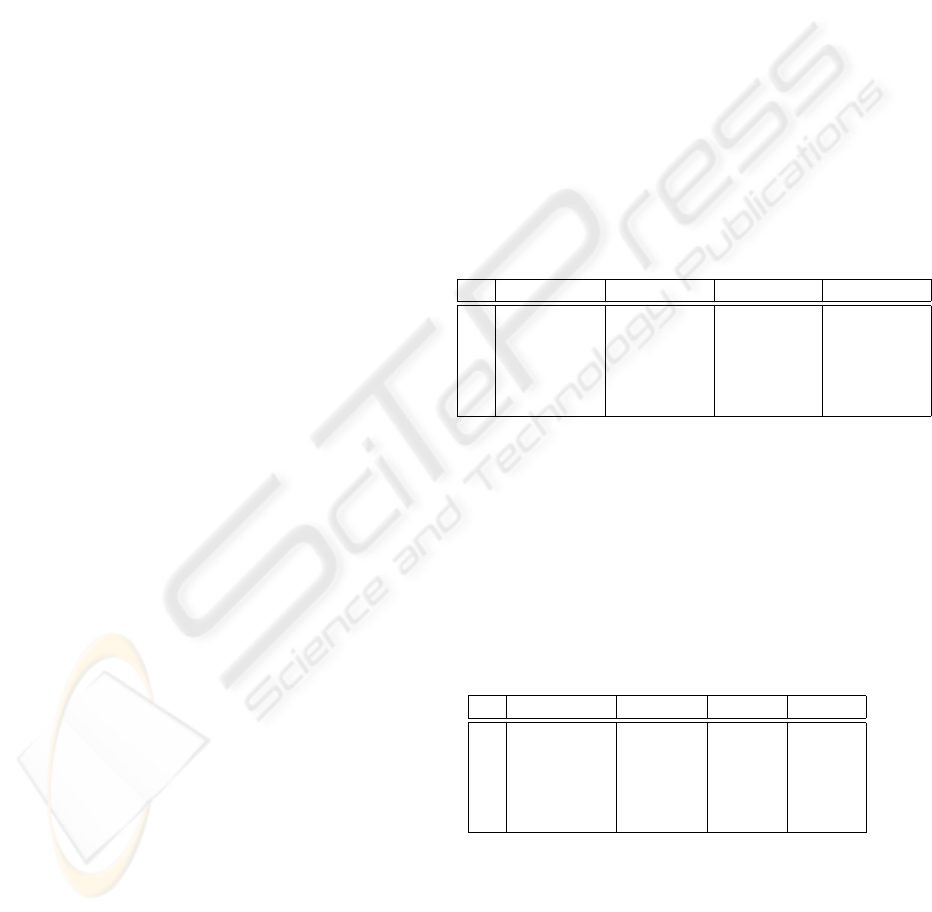
Table 1 presents the means of the score of the com-

pared algorithms (the MDL score has to be mini-

mized). The best results are presented in bold face.

Table 1: Scores

N GreedyBN TabuBN EQ LCG

1 3266.29 3262.61 3261.57 3261.57

2 3343.20 3336.69 3335.82 3335.82

3 33563.80 33553.79 33517.19 33517.19

4 139719.52 139558.86 139116,70 139116,70

5 720712.31 720383.23 720038.42 720038.42

Table 2 presents the comparison of the average ex-

ecution times of the four algorithms. They are all

programmed in Java, using the same base classes,

the same methods for computing scores and the same

caching schemas. The tabu list of TabuBN is imple-

mented as a hash table. The comparison has been re-

alized on a PIII 500Mhz CPU. The results are given

in seconds.

Table 2: Execution times

N GreedyBN TabuBN EQ LCG

1 0,23 0,25 bf 0,29 0,21

2 0,50 0,55 0,68 0,50

3 18,39 19,48 17,65 17,26

4 126,86 160,52 128,93 117,58

5 325,43 493,32 354,85 279,44

These results clearly show that EQ and LGC al-

gorithms are systematically more successful than

GreedyBN, and even TabuBN on non-trival tasks, for

execution times comparable to those of GreedyBN

and smaller than those of TabuBN. This experimen-

tal results also show that LCG approach drastically

simpliﬁes the algorithms formulation and has some

LEARNING BAYESIAN NETWORKS WITH LARGEST CHAIN GRAPHS

189

beneﬁcial aspects on their execution time than EQ al-

gorithm.

In terms of execution times, EQ-LCG3 conﬁrms its

advantage against EQ 3, suggested by the algorithmic

analysis presented in the previous section. Although

the differences of execution time that may appear to

be weak, it is the ﬁrst time, to our knowledge, that

learning algorithm in the space of equivalence classes

is faster (especially for big sized network) than the

classic greedy algorithm, that explores directly the

space of bayesian network structures.

5 CONCLUSION

In this paper, we presented a new theoretical and al-

gorithmic framework for the elaboration of bayesian

network learning algorithms in the space of equiva-

lence classes structures.

Based on largest chain graph, EQ-LCG allow to

drastically simpliﬁes the algorithms formulation and

analyses and has some beneﬁcial aspects on their ex-

ecution time.

The instantiable graph detection algorithm pro-

vides the means for the veriﬁcation of the consistency

of the obtained largest chain graphs.

REFERENCES

Bendou, M. and Munteanu, P. (2002). Modles

graphiques semi-orients pour l’apprentissage des

rseaux baysiens”. EGC 2002, Montpellier.

Chickering, D. (1996). Learning equivalence classes of

bayesian-network structures. In Proc. of the 12th

Conf. on Uncertainty in Artiﬁcial Intelligence. Mor-

gan Kaufmann.

Friedman, N. and Goldszmidt, M. (1996). Learning

bayesian networks with local structure. In Proc. of the

12th Conf. on Uncertainty in Artiﬁcial Intelligence.

Morgan Kaufmann.

Frydenberg, M. (1990). The chain graph markov property.

Scandinavian Journal of Statistics, 17:333–353.

Munteanu, P. and Bendou, M. (2001). The eq framework for

learning equivalence classes of bayesian networks. In

Proc. of the 2001 IEEE International Conference on

Data Mining. IEEE Computer Society.

Spirtes, P., Glymour, C., and Scheines, R. (1993). Causa-

tion, Prediction and Search. Springer-Verlag.

Verma, T. and Pearl, J. (1990). Equivalence and synthesis

of causal models. In Proc. of the 6th Conf. on Uncer-

tainty in Artiﬁcial Intelligence. Elsevier.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

190