TOWARDS HIGH DIMENSIONAL DATA MINING WITH

BOOSTING OF PSVM AND VISUALIZATION TOOLS

Thanh-Nghi Do, François Poulet

ESIEA Recherche, 38 rue des Docteurs Calmette et Guérin, 53000 Laval, France

ywords: Data mining, Classification, Machine learning, SVM, Incremental learning, Boosting, Visualization.

Abstract: We present a new supervised classification algorithm using boosting with support vector machines (SVM)

and able to deal with very large data sets. Training a SVM usually needs a quadratic programming, so that

the learning task for large data sets requires large memory capacity and a long time. Proximal SVM

proposed by Fung and Mangasarian is another SVM formulation very fast to train because it requires only

the solution of a linear system. We have used the Sherman-Morrison-Woodbury formula to adapt the PSVM

to process data sets with a very large number of attributes. We have extended this idea by applying boosting

to PSVM for mining massive data sets with simultaneously very large number of datapoints and attributes.

We have evaluated its performance on several large data sets. We also propose a new graphical tool for

trying to interpret the results of the new algorithm by displaying the separating frontier between classes of

the data set. This can help the user to deeply understand how the new algorithm can work.

1 INTRODUCTION

In recent years, real-world databases increase rapidly

(double every 9 months). So the need to extract

knowledge from very large databases is increasing.

Knowledge Discovery in Databases (KDD) can be

defined as the non-trivial process of identifying

valid, novel, potentially useful, and ultimately

understandable patterns in data (Fayyad et al., 1996).

Data mining is the particular pattern recognition task

in the KDD process. It uses different algorithms for

classification, regression, clustering or association.

Support Vector Machine (SVM) algorithms

proposed by (Vapnik, 1995) are a well known class

of classification algorithms using the idea of kernel

substitution. SVM solutions are obtained from

quadratic programming problems possessing a

global solution. Therefore, the learning task for large

data sets requires large memory capacity and a long

time. There is a need to scale up SVM algorithms to

handle massive data sets on personal computers. The

proximal SVM proposed by (Fung & Mangasarian,

2001) changes the inequality constraints to equalities

in the optimization problem, thus the training task

requires the solution of a system of linear equations,

so that PSVM is very fast to train. Furthermore,

PSVM can construct incrementally the model

without loading the whole data set in main memory.

The Sherman-Morrison-Woodbury formula (Golub

& van Loan, 1996) is used to adapt PSVM to a row-

incremental or column-incremental version (but not

both). The new boosting of PSVM algorithm we

present in this paper focuses on mining massive data

sets with simultaneously very large number of

datapoints and attributes. Some performances are

evaluated on UCI (Blake & Merz, 1998), Twonorm,

Ringnorm (Breiman, 1996), Reuters-21578 and Ndc

(Musicant, 1998) data sets. The results are compared

with LibSVM (Chang & Lin, 2003). However, for

many data mining applications, understanding the

model obtained by the algorithm is as important as

the accuracy. In this order, we also propose a

graphical tool for trying to explain the result of the

boosting of PSVM by displaying the separating

frontier between classes. This can help the end-user

to deeply understand how, why the algorithm works

so well.

We briefly summarize the content of the paper now.

In section 2, we introduce standard SVM and

proximal SVM algorithms. In section 3, we describe

row-incremental and column-incremental linear

PSVM. In section 4, we apply the boosting approach

to PSVM. In section 5, we present the visualization

tool for trying to explain the results. We demonstrate

numerical test results in section 6 before the

Do T. and Poulet F. (2004).

TOWARDS HIGH DIMENSIONAL DATA MINING WITH BOOSTING OF PSVM AND VISUALIZATION TOOLS.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 36-41

DOI: 10.5220/0002639500360041

 SciTePress

conclusion in section 7. Some notations are used in

this paper. All vectors will be column vectors unless

transposed to row vector by a T superscript. The 2-

norm of the vector x will be denoted by ||x||, the

matrix A[mxn]

will be m trained points in the n-

dimensional real space R

. The classes +1, -1 of m

trained points are denoted by the diagonal matrix

D[mxm] of +1, -1. e will be the column vector of 1.

w, b will be the coefficients and the scalar of the

hyper plan. z will be the slack variable and

is a

positive constant. I denote the identity matrix.

2 PROXIMAL SVM

We briefly present a general linear classification task

of SVM and then we summarize proximal SVM

algorithm.

2.1 Linear SVM Classification

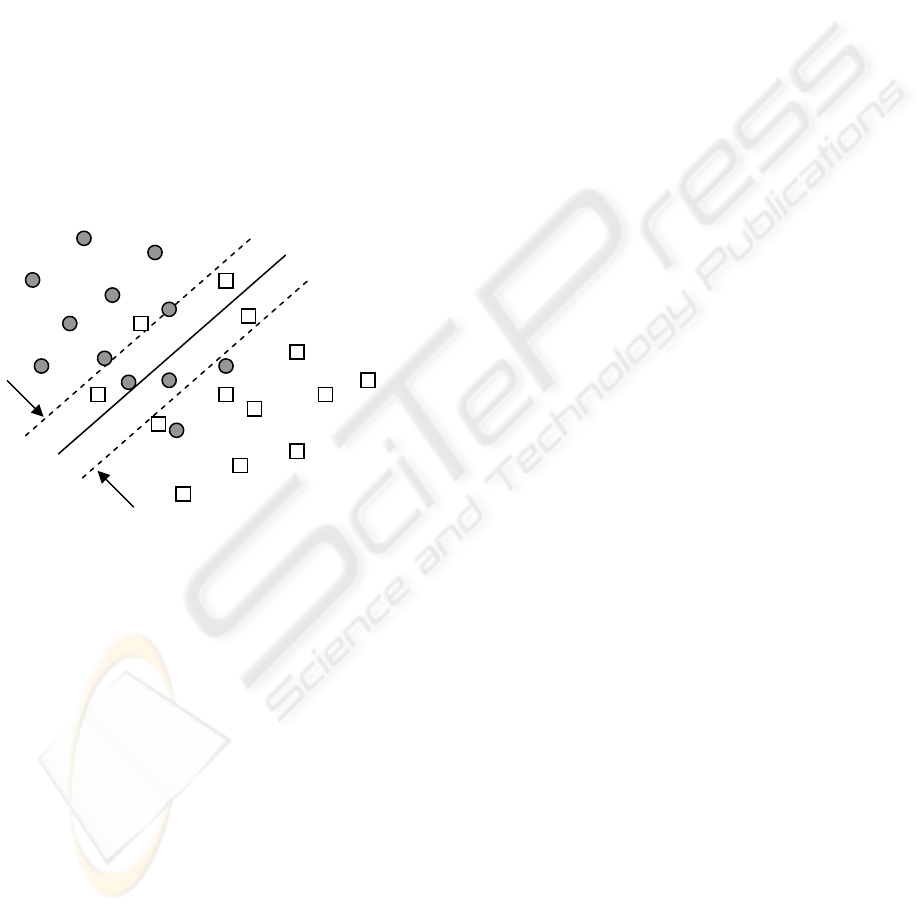
Let us consider a linear binary classification task, as

depicted in figure 1, with m data points in the n-

dimensional input space R

, represented by the mxn

matrix A, having corresponding labels ±1, denoted

by the mxm diagonal matrix D of ±1. For this

problem, the SVM try to find the best separating

plane, i.e. furthest from both class +1 and class -1. It

can simply maximize the distance or margin

between the support planes for each class (x

.w–

b=+1 for class +1, x

.w–b=-1 for class -1). The

margin between these supporting planes is 2/||w||.

Any point falling on the wrong side of its supporting

plane is considered to be an error. Therefore, the

standard SVM algorithm with linear kernel needs to

simultaneously maximize the margin and minimize

the error. This is accomplished through the

following quadratic program (1):

min f(z,w,b) = νe

z + (1/2)||w||

s.t. D(Aw - eb) + z ≥ e (1)

where the slack variable z ≥ 0 and

is a positive

constant. The plane (w,b) is obtained by the solution

of the quadratic program (1). And then, the

classification function of a new data point x based on

the plane is: f(x) = sign(x.w – b) (2)

SVM can use some other classification functions, to

change from a linear to non-linear classifier, one

must only substitute a kernel evaluation in the

objective function instead of the original one. More

details about SVM and others based-kernel learning

methods can be found in (Cristianini & Shawe-

Taylor, 2000).

2.2 Proximal SVM classifier

The proximal SVM classifier proposed by (Fung &

Mangasarian, 2001) changes the inequality

constraints to equalities in the optimization problem

(1). However, besides adding a least squares 2-norm

error into the objective function f, it changes the

formulation of the margin maximization to the

minimization of (1/2)||w,b||

. Thus substituting for z

from the constraint in terms (w,b) into the objective

function f we get an unconstraint problem (3):

min f(w,b)= (ν/2)||e – D(Aw–eb)||

+ (1/2)||w,b||

(3)

Setting the gradient with respect to (w,b) to zero

gives:

.. w

= (I/ν + E

-1

De (4)

where E = [A -e]

Therefore, the linear PSVM is very fast to train

because it expresses the training in terms of solving

a set of linear equations of (w,b) instead of quadratic

programming. The accuracy can be compared with

standard SVM. Note that all we need to store in

memory is the (m)x(n+1) training data matrix E, the

(n+1)x(n+1) matrix E

E and the (n+1)x1 vector d =

De. If the dimension of the input space is small

enough (less than 10

), even if there are millions

datapoints, PSVM is able to classify them on a

standard personal computer. For example, the linear

PSVM can easily handle large data sets as shown by

A+

.w – b = 0

–

b = +1

–

b =

margin = 2/||w||

Figure 1: Linear separation of the datapoints into two

classes

TOWARDS HIGH DIMENSIONAL DATA MINING WITH BOOSTING OF PSVM AND VISUALIZATION TOOLS

the classication of 2 million 10-dimensional points

in 15 seconds on a Pentium-4 (2.4 GHz, 256 Mb

RAM, Linux). In order to deal with very large (at

least one billion points) data sets, the incremental

version is extended from the computation of E

and d=E

De.

3 INCREMENTAL PSVM

3.1 Row-incremental PSVM

(Fung and Mangasarian,2002) have proposed to split

the training data set E into blocks of lines E

, D

and

compute E

E and d=E

De from these blocks : E

E =

∑ E

and d = ∑ d

= ∑ E

e. For each step, we

only need to load the (blocksize)x(n+1) matrix E

and the (blocksize)x1 vector D

e for computing E

and d=E

De. We only need to store in memory

(n+1)x(n+1) and (n+1)x1 matrices although the

order of the data set is one billion data points. The

authors have performed the linear classification of

one billion data points in 10-dimensional input space

into two classes in less than 2 hours and 26 minutes

on a Pentium II.

3.2 Column-incremental PSVM

The algorithm described in the previous section can

handle data sets with a very large number of

datapoints and small number of attributes. But some

applications (like bioinformatics or text mining)

require data sets with a very large number of

attributes and few training data. To adapt the

algorithm to this problem, we have applied the

Sherman-Morrison-Woodbury formula to the linear

equation system (4) to obtain:

.. w

= (I/ν + E

-1

= νE

[De – (I/ν + EE

)

-1

De] (5)

where E = [A -e]

The solution of (5) depends on the inversion of the

(m)x(m) matrix (I/ν + EE

) instead of the

(n+1)x(n+1) matrix (I/ν + E

E) in (4). The cost of

storage and computation depends on the number of

training data. This formulation can handle data sets

with very large number of attributes and few training

data. We have imitated the row-incremental

algorithm for constructing the column-incremental

algorithm able to deal with very large number of

dimensions. The data are split in blocks of columns

and then we perform the incremental computation

of EE

= ∑ E

. For each step, we only need to

load the (m)x(blocksize) matrix E

for computing

. Between two incremental steps, we need to

store in memory the (m)x(m) matrix EE

although

the order of the dimensional input space is very

high. With these two formulations of the linear

incremental PSVM, we are able to deal with very

large data sets (large either in training data or

number of attributes, but not yet both

simultaneously). We have used them to classify bio-

medical data sets with interesting results in terms of

learning time and classification accuracy (Do &

Poulet, 2003). The parallel and distributed version of

the two incremental PSVM algorithms can be found

in (Poulet & Do, 2003) and (Poulet, 2003).

4 BOOSTING OF PSVM

For mining massive data sets with simultaneously

large number (at least 10

) of datapoints and

attributes, there are at least two problems to solve:

the learning time and the memory requirement. The

PSVM algorithm and its incremental versions need

to store and invert a matrix with size mxm (or nxn).

To scale PSVM to large data sets, we have applied

the boosting approach to the PSVM algorithm. We

briefly explain the mechanism of boosting of PSVM,

more details about boosting can be found in (Freund

& Chapire, 1999). Boosting technique is a general

method for improving the accuracy of any given

learning algorithm. The boosting algorithm calls

repeatedly a given weak or base learning algorithm k

times so that each boosting step concentrates mostly

on the errors produced by the previous step. For

achieving this goal, we need to maintain a

distribution weights over the training examples.

Initially, all weights are set equally and at each

boosting step the weights of incorrectly classified

examples are increased so that the weak learner is

forced to focus on the hard examples in the training

set. The final hypothesis is a weighted majority vote

of k weak hypotheses. Alternately, we consider the

PSVM algorithm as a weak algorithm thus at each

boosting step we can sample a subset of the training

set according to the distribution weights over the

training examples. Note that PSVM only classifies

the subset (less than the original training set). The

subset size is in opposite proportion to the number of

boosting steps. Row-incremental or Column-

incremental PSVM can be adapted to solve large

sizes of subset with high performances concerning

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

the learning time, the memory requirements and the

classification accuracy.

5 VISUALIZATION TOOL TO

EXPLAIN BOOSTING RESULTS

For many data mining applications, understanding

the model obtained by the algorithm is as important

as the accuracy, it is necessary that the user has

confidence in the knowledge discovered (model) by

data mining algorithms. This can help to reduce the

risk of wrong decisions or incorrect assumptions

made during the mining task. Although SVM and

boosting algorithms have been successfully applied

to a number of applications, they provide limited

information. Most of the time, the user only knows

the classification accuracy. It is difficult to really

explain or verify the constructed model or

understand why the SVM and boosting algorithms

are more efficient than the other ones. Information

visualization methods can be used to improve the

results comprehensibility. There are very few

research papers about the visualization of SVM

(Poulet, 2003a) or boosting results. So we have

developed a new method that can help the user to

understand the model constructed by our boosting of

PSVM algorithm. No single visualization method is

best for high-dimensional data mining. This implies

that we should design a visualization tool which

combines forces from an arsenal of visualization

methods. We propose to use data distribution

according to predictive value with 2D-scatterplot

matrices method. The understanding can be greatly

enhanced by visualizing the same information in

different ways. Each view provides the user with

useful information. While the classification task is

processed (based on the model obtained), we also

compute the distribution of the points according to

predictive value. For each class, the positive

distribution is the set of correctly classified data

points, and the negative distribution is the set of

misclassified data points as shown in figure 2.

Datapoints being near the frontier between classes

correspond to bar charts being near the origin. When

these bar charts are selected, the corresponding

datapoints are displayed in all possible pair wise

combinations of dimensions in 2D-scatterplot

matrices. The user can see approximative frontier

between classes. This can help the user to improve

the comprehensibility of the obtained model, his

confidence in the knowledge discovered is

increased. The visualization tool has been applied to

the Segment data set of Statlog. This data set has

2310 datapoints, 19 attributes and 7 classes. We

consider the class 2 as +1 class and all others classes

are considered as -1 class. Our boosting of PSVM

algorithm is used to classify this data set. The

understanding of the result is enhanced in our

visualization tool as shown in the figure 3.

6 NUMERICAL TEST RESULTS

The software program is implemented in C/C++ on

PC (Linux). We are interested in the evaluation of

the performances concerning the learning time, the

accuracy and the memory requirements. We have

selected 3 synthetic data sets generated by

Twonorm, Ringnorm, NDC and 8 data sets from the

UCI repository. These data sets are described in

table 1. Nominal attributes from the Adult and

Mushroom datasets are converted into binary

attributes. We have used the new boosting of linear

PSVM (Boost-PSVM) and LibSVM with linear

kernel to classify data sets on a Pentium-4 machine,

2.4 GHz CPU, and 256 MB RAM. The first small

data sets are used to evaluate the classification

accuracy, learning time shown in table 2. Boost-

PSVM is outperforming LibSVM in six data sets on

Table 1: Data sets description

Class

Rows Attr. method

Twonorm 2 7400 20 300 / 7100

Ringnorm 2 7400 20 300 / 7100

Pima 2 768 8 10-fold

Bupa 2 345 6 10-fold

Ionosphere

2 351 34 10-fold

Mushroom

2 8124 22 10-fold

Tic-tac-toe

2 958 9 10-fold

Adult 2 48842 14 32561/16281

Reuters 135 10789 29406 7770 / 3019

Forest 8 581012 54 10-fold

Ndc 2 55000 20000 50000 / 5000

misclassification

nb. points

predictive value

–

correct classification

Figure 2: Data distribution according to predictive value

TOWARDS HIGH DIMENSIONAL DATA MINING WITH BOOSTING OF PSVM AND VISUALIZATION TOOLS

classification correctness and four data sets on

learning time. Note that the training time of LibSVM

increases dramatically with the size of the training

data. For example for the Adult data set, Boost-

PSVM is a factor of 190 faster than LibSVM.

We have used the Bow software program

(McCallum, 1998) to pre-process the Reuters-21578

data. Each document is represented as a vector of

words. Thus we have obtained 29406 words

(attributes) without any feature selection. We have

classified the 10 largest categories. This data set has

more than 2 classes so we used the one-against-all

approach. The most popular measures are based on

Precision and Recall. The table 3 reports the average

of Precision and Recall (breakeven point). Boost-

PSVM has given the best accuracy on 9 of 10

categories. However, the learning time of Boost-

PSVM is twice as LibSVM one because the Boost-

PSVM needs many boost steps to achieve a good

classification correctness.

Two very large data sets are used to estimate the

execution time and memory requirements of the

algorithms. LibSVM loads the whole data set in the

memory so we have increased the capacity of RAM.

For Forest cover type data set, we have classified the

2 largest classes (Spruce-Fire: 211840 rows and

Lorgepole-Pine: 283301 rows with 54 attributes).

We have generated a large data set with 55000

points, 20000 attributes and 2 classes (about 4 GB)

with NDC. For both data sets, LibSVM has not

finished its learning task. For classifying Forest

cover type data, LibSVM was running during 21

days without any result. For the NDC data set,

loading the whole data in memory requires at least

4 GB RAM, so we could not obtain any result with

LibSVM. Our Boost-PSVM algorithm only needs

256 MB of RAM but it had to read data for each

boosting step (96 % of the time was spent to read

data from disk). Finally, the results in table 4 show

that Boost-PSVM is able to mine massive data sets

with simultaneously very large number of datapoints

and attributes on PCs in acceptable execution time.

7 CONCLUSION

We have developed a new boosting of PSVM able to

classify very large data sets on personal computers.

The main idea is to extend PSVM algorithms with

boostong for scaling data mining algorithms to

massive data sets. Numerical test results have shown

that the new boosting of PSVM algorithm is fast and

accurate. It was compared with LibSVM. For small

size data sets, it preserves learning speed and

classification correctness. The new algorithm has

also shown effectiveness concerning the execution

time, the memory requirement and the accuracy for

massive data sets with simultaneously very large

number of datapoints and attributes. We also

proposed a visualization tools for trying to interpret

the results of PSVM. A multiple views approach is

used to display the frontier between classes. This can

help the user to understand how and why the

algorithm works so well. This avoids using

automatic mining algorithm as a “black box”.

Forthcoming improvements will be to extend this

algorithm to build parallel and distributed algorithms

and to combine our method with other graphical

techniques (Fayyad et al., 2001), (Poulet, 2002) to

construct another kind of cooperation between SVM,

boosting and visualization tools.

Table 2

Performance of Boost

PSVM and

LibSVM on small data sets

Time (secs) Accuracy (%)

Boost

PSVM

Lib

SVM

Boost

PSVM

Lib

SVM

Twonorm 0,06

0,03 97,04

97,01

Ringnorm

0,14

0,23

75,07

73,82

Pima 0,088

0,085 77,50

76,82

Bupa 0,043

0,019 69,12

68,41

Ionosphere

0,106

0,044

88,00

88,32

Mushroom

1,528

3,75

100,00

Tic-tac-toe

0,089

0,323

65,63

65,34

Adult

12,86

2472 85,25

85,29

Table 4 – BoostPSVM results on large data sets

Table 3

Breakeven performance for the 10 largest

categories of Reuters-21578

Accuracy (%) Time(secs)

Boost

PSVM

LibSVM

Boost

PSVM

LibSVM

Earn

98.41

98.02

8,42

9,4

Acq

96.57

95.66

8,47

10,78

Money-fx

79.49

75.72 7,68

7,4

Grain

90.75

89.33 9,86

5,05

Crude

89.83

86.62 8,05

5,7

Trade

78.18

77.46 8,01

5,73

Interest

78.32

75.57 13,33

8,69

Ship

84.60

83.00 14,21

5,36

Wheat

86.38

85.58 14,10

3,54

Corn 88.97

88.99

6,28

3,79

RAM(MB) Accuracy (%) time (min)

Forest

19 77.41 23,2

Ndc 193 81,18 1491,2

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

Acknowledgements. Thanks to Jason Rennie for his

help with preparing Reuters-21578 text collection.

REFERENCES

Blake, C., Merz, C., 1998. UCI Repository of Machine

Learning Databases.

Breiman, L., 1996. Bias, Variance and Arcing Classifiers.

In Technical Report 460, Statistics Department,

University of California.

Chang, C-C., Lin C-J., 2003. A Library for Support Vector

Machines. http://www.csie.ntu.edu.tw/~cjlin/libsvm

Cristianini, N. and Shawe-Taylor, J., 2000. An

Introduction to Support Vector Machines and Other

Kernel-based Learning Methods. Cambridge

University Press.

Do, T-N., Poulet, F., 2003. Incremental SVM and

Visualization Tools for Bio-medical Data Mining. In

proc. of Workshop on Data Mining and Text Mining

in Bioinformatics, ECML/PKDD’03, Cavtat-

Dubrovnik, Croatia, pp. 14-19.

Fayyad, U., Grinstein, G., Wierse, A., 2001. Information

Visualization in Data Mining and Knowledge

Discovery. Morgan Kaufmann Publishers.

Fayyad, U., Piatetsky-Shapiro, G., Smyth, P., Uthurusamy,

R., 1996. Advances in Knowledge Discovery and Data

Mining. AAAI Press.

Freund, Y., Chapire, R., 1999. A Short Introduction to

Boosting. In Journal of Japanese Society for Artificial

Intelligence, 14(5), pp. 771-780.

Fung, G., Mangasarian, O., 2001. Proximal Support

Vector Machine Classifiers. In proc. of the 7

ACM

SIGKDD Int. Conf. on KDD’01, San Francisco, USA,

pp. 77-86.

Fung, G., Mangasarian, O., 2002. Incremental Support

Vector Machine Classification. In proc. of the 2

SIAM Int. Conf. on Data Mining SDM'2002

Arlington, Virginia, USA, pp. 247-260.

Golub, G., van Loan, C., 1996. Matrix Computations. John

Hopkins University Press, Baltimore, Maryland, 3

Edition.

McCallum, A., 1998. Bow: A Toolkit for Statistical

Language Modeling, Text Retrieval, Classification and

Clustering. http://www-2.cs.cmu.edu/~mccallum/bow

Musicant D., 1998. NDC : Normally Distributed Clustered

Data sets. http://www.cs.wisc.edu/~musicant/data/ndc/

Poulet, F., 2002. Full-View: A Visual Data Mining

Environment. In Int. Journal of Image and Graphics,

2(1), pp. 127-143.

Poulet, F., 2003. Multi-way Distributed SVM Algorithms.

In proc. of Workshop on Parallel and Distributed

Computing for Machine Learning, ECML/PKDD’03,

Cavtat-Dubrovnik, Croatia, pp. 59-70.

Poulet, F., Do, T-N., 2003. Mining Very Large Data sets

with Support Vector Machine Algorithms. In

Enterprise Information Systems V, Kluwer.

Vapnik, V., 1995. The Nature of Statistical Learning

Theory. Springer-Verlag, New York.

Figure 3: Visualization of the Boost-PSVM result on Segment dataset

TOWARDS HIGH DIMENSIONAL DATA MINING WITH BOOSTING OF PSVM AND VISUALIZATION TOOLS