A CONNEXIONIST APPROACH FOR CASE BASED REASONING

Antonio B. Bailón Miguel Delgado Eva Gibaja

Dpto. Ciencias de la Computación e Inteligencia Artiﬁcial

E.T.S. Ingeniería Informática, Universidad de Granada

c/ Daniel Saucedo Aranda s/n, 18071 Granada (Spain)

José María de la Torre

Dpto. Economía Financiera y Contabilidad

Facultad de Ciencias Económicas, Universidad de Granada

Campus Universitario de La Cartuja, 18071 Granada (Spain)

Keywords:

Case Based Reasoning, Associative Memories, Connexionist Model

Abstract:

Case Based Learning is an approach to automatic learning and reasoning based on the use of the knowledge

gained in past experiences to solve new problems. To suggest a solution for a new problem it is necessary

to search for similar problems in the base of problems for which we know their solutions. After selecting

one or more similar problems their solutions are used to elaborate a suggested solution for the new problem.

Associative memories recover patterns based on their similarity with a new input pattern. This behaviour made

them useful to store the base of cases of a Case Based Reasoning system. In this paper we analyze the use

of a special model of associative memory named CCLAM (Bailón et al., 2002) with this objective. To test

the potentiality of the tool we will discuss its use in a particular application: the detection of the “health” of a

company.

1 INTRODUCTION

In real life, when we have to deal with a problem our

memory evokes past similar situations. Those simi-

lar problems were solved in the past and now we re-

member the actions that helped us to solve them (or at

least we remember the actions that we tried but didn’t

solve the problems). If a new problem is similar to a

problem that was previously solved we can reuse its

solution (possibly after revising it) to solve the current

problem. If our actions are successful we will remem-

ber them if we need to solve a similar problem.

Case based reasoning relies on the existence of a

base of cases that stores our experience in a particular

problem. When a new problem arrives, the base is

searched for a similar case to reuse its solution. New

cases are stored in the base of cases when they are

solved (Aamodt and Plaza, 1994).

The role of the memory is very important because

the process relies on its behaviour storing cases and

retrieving cases based on their similarity with a new

one. Associative memories receive an input patern

and retrieve the most similar stored pattern. This is

the expected behaviour of the base of cases in case

based reasoning and that’s why we use associative

memories.

2 CONTINUOUS CLASSIFYING

ASSOCIATIVE MEMORY

The Continuous Classifying Associative Memory

CCLAM is a memory model which allows the stor-

age of arbitrary analogical patterns which have con-

tinuous components in the interval [0, 1].

b b

CLASSIFICATION

RECOVERY

Figure 1: Continuous Classifying Associative Memory

(CCLAM).

In the operation of the CCLAM we can distinguish

two processes: classiﬁcation and recovery. The clas-

369

B. Bailón A., Delgado M., Gibaja E. and María de la Torre J. (2004).

A CONNEXIONIST APPROACH FOR CASE BASED REASONING.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 369-374

DOI: 10.5220/0002641403690374

 SciTePress

siﬁcation process receives an input pattern in the F

layer (Fig.1) and obtains a value in each processing el-

ement (PE) of F

which indicates the degree to which

the input pattern is similar to the stored pattern repre-

sented by this PE. The recovery process receives in

the extent to which we refer to each of the stored

patterns and recovers a combination of these patterns

in F

The F

layer is competitive. The weights of the

competition signals between the PEs of the F

layer

are represented in the matrix β

n×n

, with n being the

number of stored patterns and β

being the weight of

the connection which exists from b

to b

. The win-

ning element is the one whose activation state Y

ver-

iﬁes Y

≥ Y

∀j. For the competition we can

establish whether the winning PE will retain its acti-

vation state or take the value 1 as its new state.

The behavior of the CCLAM depends on:

• The weigths of the connections made between the

layers F

and F

, represented in the matrix M

• The functions Υ and Ψ that control the propagation

of the information between the layers.

• The weigths of the competition connections made

in the F

layer.

• Whether the winning PE in F

will retain its value

or take value 1.

This behavior of the classiﬁcation and recovery

processes may be different. To distinguish the

weights and functions used in each process we will

name them using the superscripts C and R appropi-

ately.

2.1 Learning

In the learning process, the memorization of a pat-

tern entails the creation of a new PE in F

and the

appropriate adjustment of the weights of the connec-

tions which are carried out towards it. Learning has

the following steps:

1. Arrival at F

of a pattern to be memorized.

2. Veriﬁcation that the pattern was not previously

stored.

3. Creation of a new PE in F

associated to the pat-

tern.

4. Adjustment of the competition weights of the F

layer.

5. Adjustment of the weights of the connections made

between F

and the new PE.

2.2 Classiﬁcation

In the classiﬁcation process the PEs send activation

signals from the F

layer towards the F

layer. Given

an input pattern presented in the F

layer activation

states are obtained in the F

layer which represent the

similarity which exists between the input pattern and

each of the stored patterns. The classiﬁcation process

has the following steps:

1. A pattern X = (x

, . . . , x

) arrives at the F

layer.

2. The signal propagates towards the F

layer so that

the PE b

receives the activation signal:

(a) y

= Ψ

, m

¢ª

j=1...p

(b) Υ

and Ψ

are functions bounded to the interval

[0, 1]. The choice of these functions depends on

the behavior which we would like the memory to

present.

3. The PEs of the F

layer compete amongst them-

selves with the intensity reﬂected in the weights

matrix β

4. We obtain the result of the classiﬁcation process in

the F

layer. The activation state obtained in the

PEs of the F

layer indicates the degree to which

the input pattern is classiﬁed by each of the classes

represented by the stored patterns.

2.3 Recovery

In the recovery process, the information ﬂows from

to F

. In the F

layer is presented an input pat-

tern which represents the degree to which recovery

involves each of the stored patterns. The recovery has

the following steps:

1. A pattern Y = (y

, . . . , y

) arrives at the F

layer.

2. The PEs of the F

layer compete amongst them-

selves with the weights matrix β

. The new acti-

vation states form the pattern Y

= (y

, . . . , y

3. The signal propagates from the F

layer towards

the F

layer so that the PE a

receives the activa-

tion signal:

(a) x

= Ψ

, m

¢ª

j=1...n

(b) Υ

and Ψ

are functions bound to the interval

[0, 1].The choice of these functions depends on

the behavior which we would like the memory

to present.

4. We obtain the pattern resulting from the recovery

process in the F

layer. This might be one of the

stored patterns or a combination of them.

3 CASE BASED REASONING

USING CCLAM

Our goal is to use the CCLAM in case-based reason-

ing to allow to:

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

370

• Store the patterns included in the set of known

cases.

• Compute the similarity that exists between a new

case and each of the stored cases.

• Select the cases that will take part in the elaboration

of the solution proposed for a new case.

• Obtain the proposed solution as the solution or

combination of solutions of several known cases.

• Store the new cases.

• Forget the cases that don’t provide a solution dif-

ferent from those provided by a large number of

the nearest known cases.

The CCLAM can store arbitrary continuous pat-

terns while other associative memories present spu-

rious states and have a strong dependency on the kind

of patterns that they can store. For that reason the

CCLAM can be used in case based reasoning allow-

ing the storage and correct retrieval of known cases.

In each case X = (x

, x

, . . . , x

) we can dis-

tinguish the attributes that deﬁne the problem from

those attributes that deﬁne the solution. Each case

X is formed by two patterns (P, S) such as P =

, p

, . . . , p

, p

∈ {x

}

j=1...n

, is the pattern

that contains the attributes of the problem and S =

, s

, . . . , s

),s

∈ {x

}

j=1...n

, contains the at-

tributes of the solution of case X.

Let’s suppose that each problem has only one solu-

tion. If we ﬁnd the same problem with two different

solutions it is possible that:

• One of the solutions embeds the other because it is

more general. We shoul decide if it is better to store

the more general or the more particular solution.

• The solutions are incompatible. The solution of a

problem can’t be used to solve the other one al-

thougt the two problems are expressed using the

same attributes. This conﬂict arises when the at-

tributes that deﬁne the problems aren’t enough to

distinguish them. To solve the conﬂict we must

augment the attributes used to represent a problem

to include those in what the actual cases differ.

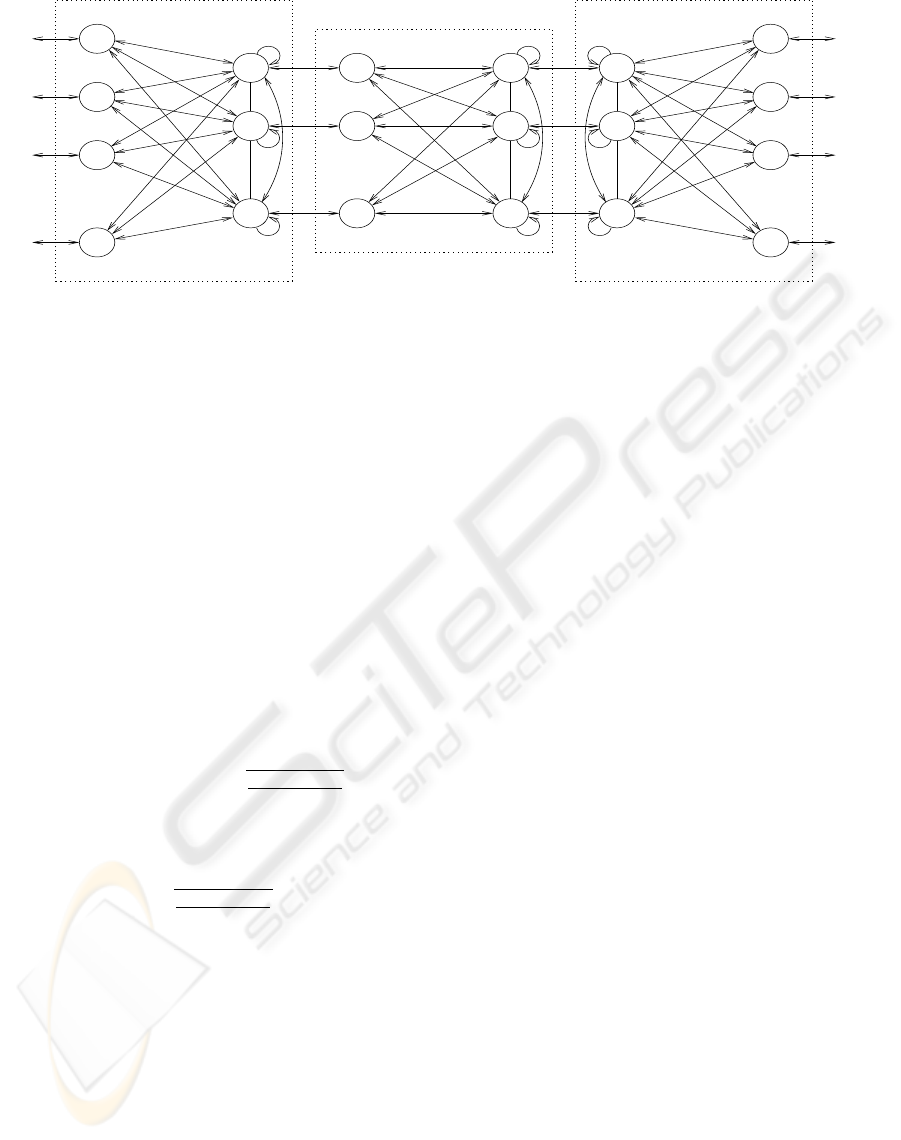
To store the cases we will use three CCLAM.

One of them will store the patterns that encode the

attributes of the problems and will be named P-

Memory. Other memory will store the attributes of

the solutions and will be named S-Memory. The

two memories will be connected by means of a third

CCLAM that selects the solution that is recovered

based on the similarities found between the stored

cases and a new problem (Fig. 2). This CCLAM that

links the P-Memory and the S-Memory will be named

L-Memory.

3.1 P-Memory

The P-Memory has as many processing elements (PE)

in the F

layer as attributes of the problem. In the F

layer has as many PE as stored problems.

The weight of the connection that links the a

PE in

the F

layer to the b

PE of layer F

represents the

value of the i-th attribute in the j-th stored problem.

In the classiﬁcation process the memory receives in

a pattern that represents a new problem and will

provide in the F

layer the degree of similarity that

exists between the new problem and each of the stored

problems.

3.1.1 Similarity between problems

In case-based reasoning it’s neccessary to compare a

new problem with all the stored problems to obtain

the similarity that exists between them. We need a

function that computes the similarity that exists be-

tween the problems. We use a function that measures

the distance between the patterns (the greater the dis-

tance between the patterns, the lower the simiarity be-

tween the problems). The most commonly used func-

tions are euclidean and manhattan distance.

We can conﬁgure the P-Memory to compute the

distance between the new problem and each known

problem. Depending on the conﬁguration we can

compute any particular instance of the Minkowski

distance ( 1 ). When p = 1 it computes the manhattan

distance and when p = 2 it computes the euclidean

distance.

(A, B) =

i=1

− b

(1)

To compute the similarity that exists between the

patterns we must take into account that the attributes

can have different relative importance. For example

lets represent the problem of selecting people to form

a basketball team based on their height and weight.

Candidates will be represented with two attributes

that measure their height in meters, weight in kilo-

grams and classiﬁcation as good or bad candidate. We

store the following cases:

Case 1 : (1.9m, 70kg, good)

Case 2 : (1.4m, 65kg, bad)

(2)

We recognize in case 1 a tall slim person and in case

2 a short fat person. When a new candidate arrives we

have to decide wether to select him for the team. The

new case (1.89m, 67kg) will be compared with cases

1 and 2 to decide its classiﬁcation. The manhattan and

euclidean distances show that the nearest stored pat-

tern is case 2. But intuitively we recognize in the new

case a tall slim person that is more similar to case 1.

A CONNEXIONIST APPROACH FOR CASE BASED REASONING

371

PROBLEM SOLUTION

LINK

Figure 2: Case Based Reasoning using CCLAM.

This happens because we have assigned the same im-

portance to the height and the weight of the person but

in this particular problem of selecting people to play

basketball the height of a person is more important

than his weigth.

((1.89, 67) , (1.9, 70)) = 3.01

((1.89, 67) , (1.9, 70)) ≈ 3

((1.89, 67) , (1.4, 65)) = 2.49

((1.89, 67) , (1.4, 65)) ≈ 2.06

(3)

We need to assign a relative importance to each at-

tribute so that the distance between patterns reﬂects it.

If we assign wheight w

to attribute p

we must con-

ﬁgure the CCLAM to compute the similarity between

patterns:

, m

) = |x

− m

, . . . , a

) = 1 −

i=1

)

i=1

(4)

The attributes of the problems are normalized to

give patterns that can be stored in the memory.

Each attribute takes its value in [0, 1] and then the

Minkowski distance

i=1

)

i=1

takes its value in

[0, 1] too. The value computed by the Ψ

function

is the similarity between the patterns measured in the

interval [0, 1].

The weights used to represent the relative impor-

tance of the attributes can be established by an ex-

pert or can be learned from the known cases. We can

use cross validation to adjust the weights. If the num-

ber of cases is high enough, when case C is removed

from the memory the rest of the cases can give the

correct solution to problem C. The goal is a weight

assignment that maximizes the number of cases that

are correctly solved if they are removed from mem-

ory. To learn the weights we can use several methods

such as simulated annealing or genetic algorithms.

The weights can be revised periodically to reﬂect the

knowledge adquired with the new cases learned after

the previous assignment of weights.

3.2 L-Memory

The CCLAM that links the P-Memory and the S-

Memory has in the F

layer one PE for each stored

problem and one PE in the F

layer for each stored

solution. There is a connection with weight 1 between

the PE in F

that represents a problem and the PE

in F

that represents the solution associated to that

problem. The rest of connections have weight 0.

The CCLAM receives in the F

layer the degree

of similarity that exists between a new problem and

each stored problem (this information comes from the

P-Memory). After the classiﬁcation process the only

active element in F

represents the proposed solu-

tion.

In some situations we can obtain the solution as

a combination of several stored solutions of similar

problems. Then we can obtain in F

the degree with

which the solutions can be combined. This can be

useful in problems where the solution is a real num-

ber that represents a physical magnitude.

3.2.1 Wheight of the environment of the

problem

Let’s suppose that a new problem P arrives. The P-

Memory ﬁnds one case with similarity 0.6 that sug-

gests solution A. It also ﬁnds 100 cases with similar-

ity 0.59 and all of them suggest solution B. Which

solution should be proposed?

The answer depends on the problem. In general we

can use a voting system. Each known problem sug-

gests its own solution with a degree that depends on

its similarity to the new problem. Then the proposed

solution will be that with the highest number of votes.

To compute the weight of a vote from the similarity

of the problem we use a non decreasing function ∆ :

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

372

[0, 1] → [0, 1] with the properties:

∆ (0) = 0

∆ (1) = 1

(5)

The L-Memory computes the sum of the degrees

with which the stored problems vote for each solu-

tion. Let’s suppose that a new case arrives and the

CCLAM that stored the problems computes the sim-

ilarities (s

, s

, . . . , s

). The L-Memory receives the

similarities in the layer F

. The weight of the con-

nection made between the i-th PE in F

and the j-th

PE in F

is m

. The memory is conﬁgured with:

, m

) = ∆ (s

) m

, x

, . . . , x

) =

i=1

(6)

After the classiﬁcation process we obtain in F

layer the degree with which each solution is sugested

by the stored cases.

If we can’t combine several solutions to obtain a

new one then we select the PE that represents the most

voted solution to be the only PE that will remain ac-

tive.

If we will combine several solutions we must adjust

the degrees with which each one is voted so that the

sum of all of them equals one to ensure that we obtain

the wheighted mean of the solutions. The result is

sent to the S-Memory.

3.3 S-Memory

The S-Memory has in the F

layer a PE for each at-

tribute of the solutions and one PE in the F

layer for

each stored solution.

The weight of the connection made between ele-

ment i in F

and element j in F

represents the value

of the j-th attribute of the i-th solution.

The recovery process obtains in F

layer the so-

lution sugested by the activation degrees received in

3.3.1 Recovery of the solution

To obtain in F

the solution that will be suggested

to solve the new problem we must conﬁgure the

CCLAM with:

, m

) = s

, x

, . . . , x

) =

i=1

(7)

This conﬁguration computes the weighted average

of the stored solutions. The weight of each solution

depends on the similarity that exists between its prob-

lem and the new case. If only one PE in F

is ac-

tive with activation 1 and the rest remain inactive the

CCLAM recovers the most voted solution.

With the recovered solution the CCLAM can show

the degree with which it was recalled. This can be

interpreted as a conﬁdence measure.

3.4 Case Pruning

The set of problems that share the same solution can

be found grouped in clusters. Those problems ly-

ing in the perimeter of the cluster are more important

because they give more information than the others.

Then if we need to reduce the number of stored cases

we can remove the cases that give less information.

To store only the new cases that give new infor-

mation we must study the solutions suggested by our

CCLAM-based CBR system. Let the solution of the

new case be A and the suggested solutions A,B,C...

suggested with degrees s(A), s(B), s(C), . . .. The

new case will be stored if the difference between the

degree of the correct solution and the sum of the de-

grees of the incorrect solutions is lower that a estab-

lished threshold.

A pattern located in the interior of a cluster makes

the correct solution be suggested with a high degree

because there are many near patterns with the correct

solution. If the pattern is near the perimeter of the

cluster then the inﬂunce of patterns with wrong solu-

tions is high.

Setting the threshold to a convenient value will for-

bid the store of patterns that are clearly in the interior

of a cluster of patterns with which it shares the same

solution.

The prune of cases must be done very carefully be-

cause we lose information when we don’t store a pat-

tern.

4 APPLICATION: A CASE STUDY

One problem that is receiving an increasing attention

in the literature is that of prediction of a company

health (behaviour).

The idea is to represent any company by a vector

, . . . , x

) of attribute values and try from that to

detect the company health.

Let us consider this health is represented in this turn

by a new boolean variable, h, such that h = 0 repre-

sents a bad health and h = 1 represents a good helth.

Clasical prediction (classiﬁcation) models try

to identify an input-output relation like h =

H (x

, . . . , x

), where function H is learned from a

set of examples by some inductive procedure.

This approach has shown some inefﬁciency be-

cause it’s very difﬁcult to capture the knowledge

about the health of a company as contained in a set

©¡

, x

, . . . , x

, h

¢ª

i=1...T

of training examples.

Semantics, scales, degree of importance, etc. of this

variables troubles us with this task. For this reason

some different approaches have raised in last years

(artiﬁcial neural networks, Kohonen maps, ...).

A CONNEXIONIST APPROACH FOR CASE BASED REASONING

373

Here we will investigate the use of our CBR ap-

proach by CCLAM to classify enterprises in the above

described sense. In the following we describe a sum-

mary of our experiment and its conclusions, being im-

possible to include here a detailed description of them

because the size and the amount of data and algorith-

mic steps.

Te interested reader may consult

http://decsai.ugr.es/ to obtain the whole set of data

and the complete discussion about the experiment.

The training set contains information about 1500

companies each described by 53 attributes. That is in

our case n = 53 and T = 1500.

The variables have very different semantics and ac-

cording to that different domains and scales. In fact

we have:

• 36 continuous attributes (ex. debt level)

• 9 integer attributes (ex. number of employees)

• 6 boolean attributes (ex. whether the company has

been audited)

• 2 categorial attributes (ex. economic activity code)

To take into account the different distance functions

(or similarity functions) needed to compare different

kinds of attributes we must conﬁgure the P-Memory

so that there will be different Ψ

and Υ

functions

depending on the kind of attribute that represents each

processing element.

We don’t know the degree of inﬂuence of each at-

tribute in the health of a company. To estimate the

relative importance of the attributes we measure the

goodness of a set of weights as the amount of correct

classiﬁcations of cases in a cross validation process.

We assume that similar companies have the same

classiﬁcation (this assumption is the key of case based

reasoning). We also assume that the number of known

cases is high enough. If the weights were right then

when we extract a case from the memory and use it as

a new problem there will be similar problems that will

classify it correctly. We repeat this operation with all

the cases and the percentage of correct classiﬁcations

is the value that measures the goodness of the set of

weights.

To ﬁnd an appropiate set of weights for the train-

ing set of cases we have used genetic algorithms to

ﬁnd initial good solutions that were then reﬁned us-

ing simulated annealing.

Once conﬁgured our CCLAM based CBR system

with the appropiate weights it was tested with a set of

764 new cases to measure the number of correct clas-

siﬁcations obtaining a 73% of success that represents

a good result that justiﬁes the use of the system.

5 CONCLUSIONS

• The CCLAM is a good choice for case based rea-

soning because it can store any number of arbitrary

cases and it don’t recover cases not stored previ-

ously because of the absence of spurious states.

• The use of two CCLAM to store the problems and

the solutions in different memories allows the cor-

rect computation ofthe similarity of the problems

and the correct retrieval of the suggested solution.

• The L-Memory allows the use of a voting system

to select the most voted of the solutions proposed

by the stored cases.

• The similarity between problems is computed by

means of the generalized minkowsky distance with

the correct conﬁguration of the P-Memory.

• When the solution is expressed with attributes that

can be aggregated we can obtain a lineal combina-

tion of the sugested solutions.

REFERENCES

Aamodt, A. and Plaza, E. (1994). Case-based reasoning:

Foundational issues, methodological variations and

system approaches. AI Communications, 7(1):39–59.

Aha, D. W. (1998). The omnipresence of case-based rea-

soning in science and application. Knowledge-Based

Systems, 11(5-6):261–273.

Aha, D. W., Kibler, D., and Albert, M. K. (1991). Instance-

based learning algorithms. Machine Learning, (6):37–

66.

Bailón, A., Delgado, M., and Fajardo, W. (2002). Con-

tinuous classifying associative memory. International

Journal of Intelligent Systems, 17(4):391–407.

Bartsch-Sprl, B., Lenz, M., and Hbner, A. Case-based rea-

soning – survey and future directions.

Globig, C. and Wess, S. (1995). Learning in case-

based classiﬁcation algorithms. In Jantke, K. P.

and Lange, S., editors, Algorithmic Learning for

Knowledge-Based Systems, volume 961, pages 340–

362. Springer-Verlag.

Leake, D. B. (1996). Case-Based Reasoning: Experiences,

Lessons, and Future Directions. MIT Press.

Richter, M. M. (1992). Classiﬁcation and learning of simi-

larity measures. Technical Report SR-92-18.

Wilson, D. R. and Martinez, T. R. (1997). Instance pruning

techniques. In Proc. 14th International Conference

on Machine Learning, pages 403–411. Morgan Kauf-

mann.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

374