ON ONTOLOGY MATCHING PROBLEMS
for building a corporate Semantic Web in a multi-communities organization
Bach Thanh Le, Rose Dieng-Kuntz, Fabien Gandon
Institut National de Recherche en Informatique et en Automatique, 2004 route des lucioles, Sophia Antipolis, France
Keywords: Semantic Web, Ontologies, Ontolog
y Matching.
Abstract: Ontologies are nowadays used in many domains such as Semantic Web, information systems… to represent
meaning of data and data sources. In the framework of knowledge management in an heterogeneous
organization, the materialization of the organizational memory in a “corporate semantic web” may require
to integrate the various ontologies of the different groups of this organization. To be able to build a
corporate semantic web in an heterogeneous, multi-communities organization, it is essential to have
methods for comparing, aligning, integrating or mapping different ontologies. This paper proposes a new
algorithm for matching two ontologies based on all the information available about the given ontologies
(e.g. their concepts, relations, information about the structure of each hierarchy of concepts, or of relations),
applying TF/IDF scheme (a method widely used in the information retrieval community) and integrating
WordNet (an electronic lexical database) in the process of ontology matching.
1 INTRODUCTION
“The Semantic Web is an extension of the current web
in which information is given well-defined meaning,
better enabling computers and people to work in
cooperation” (Berners-Lee et al. 2001).
An organization can be an actual enterprise, a
co
mmunity, a virtual enterprise consisting of several
organizations in collaboration. An heterogeneous orga-
nization can comprise various sources of knowledge,
various categories of users and various communities.
A corporate memory (or organizational memory)
can be defined
as an explicit and persistent materiali-
zation of crucial knowledge and information of an
organization in order to ease their access, sharing and
reuse by the members of the organization in their
individual and collective tasks.
By taking into account the analogy between the
resource
s of a corporate memory and the resources of
the Web, a corporate memory can be materialized in a
corporate semantic web, constituted of:
- resource
s (persons, documents (XML, HTML), or
services, software, materials),
- ontologie
s (describing the conceptual vocabulary
shared by the different communities of the organiza-
tion),
- se
mantic annotations on these resources (i.e. on
persons’ skills, document contents, characteristics of
services/software/material), relying on these
ontologies.
In the framework of knowledge management in an
heterogene
ous organization, the materialization of the
organizational memory in a “corporate semantic web”
may require to integrate the various ontologies of the
different groups (or communities) of this organization
(the various communities generally prefer to use their
own ontologies instead of a common general one).
To be able to build a corporate semantic web in an
heterogene
ous, multi-communities organization, it is
essential to have methods for manipulating the different
ontologies of the various groups of the organization, for
comparing, aligning, integrating or mapping these
different ontologies.
In this paper, we present our preliminary work on
this difficult
problem. The results presented here are a
new algorithm for matching ontologies, named ASCO.
A successful ontology matching is the basis for onto-
logy integration, ontology comparison.
Our other contributions are the application of
TF/IDF sche
me, a widely used method in the informa-
tion retrieval community, and the integration of a
lexical thesaurus (such as WordNet, EuroWordNet) in
the process of matching the ontologies.
The rest of this paper is organized as follows: some
related work i
s presented in section 2. Section 3 pre-
sents our ontology representation. Our ASCO algori-
thm is described in section 4. The experimental results
follow in section 5. And finally, section 6 summarizes
our conclusions.
236
Thanh Le B., Dieng-Kuntz R. and Gandon F. (2004).
ON ONTOLOGY MATCHING PROBLEMS - for building a corporate Semantic Web in a multi-communities organization.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 236-243
DOI: 10.5220/0002642802360243
Copyright
c
 SciTePress

2 RELATED WORK
The ontology matching problem is the problem of
finding the semantic mappings between elements of
two given ontologies. As we will discuss later, we
define an ontology as a conceptual vocabulary shared
by a community, it comprises a hierarchy of concepts
and a hierarchy of relations, enabling to describe
relationships between the concepts (see section 3).
The ontology matching problem may hence be con-
sidered as problem of matching the hierarchies of con-
cepts and the hierarchies of relations of two ontologies.
Without the hierarchy of relations, an ontology can
be regarded as a schema. In the schema matching
domain, there was a lot of researches in the context of
data integration and data translation. A good survey of
approaches to automatic schema matching is presented
in (Rahm & Bernstein 2001).
Similarity Flooding (SF) is a generic graph
matching algorithm (Melnik et al. 2001). Its application
to schema matching is presented in (Melnik et al.
2002). SF converts schemas (SQL DDL, XML) into
directed labeled graphs and then uses fix-point compu-
tation to determine correspondent nodes in the graphs.
This approach is based on a very simple string compa-
rison of node’s names to calculate initial element-level
mappings, then the last is fed to the structural SF
matcher. Although SF applied a new oriented-structural
approach based on the intuition that elements of two
distinct schemas are similar when their adjacent ele-
ments are similar to propagate the similarity of two
elements to their respective neighbors, it relies mainly
on labels of arcs. If there is no label for arcs in the
graph or if these labels are almost the same, the algori-
thm does not work well. Without use of an external ter-
minological dictionary (such as WordNet), the algori-
thm will not give good linguistic-level matching results
in the first phase, which will be fed to the second pha-
se, so the final results will be influenced. Consequently,
the application of SF in the ontology matching domain
(where it is difficult to build labeled graphs) will en-
counter many hard problems and requires a lot of work.
Contrarily to SF, Cupid (Madhavan et al. 2001)
proposes a match approach combining a sophisticated
name matcher and a structural match algorithm. Cupid
is also a generic schema matching but its structural
matching phase is mainly based on the similarity of
atomic elements in the graphs (i.e. leaves). So if there
are significant differences in structure of the given
graphs, Cupid cannot find correct mappings. For
example, if a concept is situated in a leaf in the first
graph (schema), but in the second, is non-leaf element
which is the root of a sub-graph, Cupid will not detect
that they are the same concept.
There is not very much work in the ontology
matching domain. Some of recent researches are GLUE
(Doan et al. 2002), Anchor-PROMPT (Noy & Musen
2001) and SAT (Giunchiglia & Shvaiko 2003).
GLUE (Doan et al. 2002) is the evolved version of
LSD (Doan et al. 2001) whose goal is to semi-
automatically find schema mappings for data integra-
tion. Like LSD, GLUE use machine learning techni-
ques to find mappings. In GLUE, there are several lear-
ners, which are trained by data instances of ontologies.
After learning phase, different characteristic instance
patterns and matching rules for single elements of the
target schema are discovered. The predictions of indivi-
dual matchers are combined by a meta-learner, and
from that, final mappings result will be deduced. One
disadvantage of this approach is that it mainly rely on
the data instances of the ontologies, which are not al-
ways abundantly available for numerous ontologies.
Another disadvantage is that the ontology is modeled
as a taxonomy of concepts and each concept has some
attributes. With this organization, GLUE does not use
information contained in the taxonomy (hierarchy) of
relations. GLUE also makes modest use of the informa-
tion about the taxonomy of concepts.
Anchor-PROMPT (Noy & Musen 2001) constructs
a directed labeled graph representing the ontology from
the hierarchy of concepts (called classes in the algori-
thm) and the hierarchy of relations (called slots in the
algorithm), where nodes in the graph are concepts and
arcs are relations denoting relationships between con-
cepts (the labels are the names of the relations). An
initial list of anchors-pairs of related concepts defined
by the users or automatically identified by lexical mat-
ching is the input for the algorithm. Anchor-PROMPT
analyzes then the paths in the sub-graph limited by the
anchors and it determines which concepts frequently
appear in similar positions on similar paths. Basing on
these frequencies, the algorithm decides if these con-
cepts are semantically similar concepts. However,
Anchor-PROMPT finds only concept mappings, not
relation mappings and it uses relation names for labels
on the arcs and simple string comparison of these
labels. So if the relation names are differently defined,
the algorithm will not work well. The returned results
of the algorithm will also be limited if the structures of
the ontologies are different (e.g. one is deep with many
inter-linked concepts, and the other is shallow). For
example, the algorithm will get problems if a hierarchy
has only a few levels and most of the relations are
associated with the concepts at the top of the hierarchy.
SAT (Giunchiglia & Shvaiko 2003) takes as input
two graphs of concepts, and produces as output rela-
tionships such as equivalence, overlapping, mismatch,
more general and more specific between two concepts.
The main idea of this approach is to use logic to encode
the concept of a node in the graph and to use SAT to
find relationships. The concept at a node, which is then
transformed into a propositional formula, is the con-
junction of all the concepts of the nodes on the path
from the root of the graph to that node. The concept of
a node, in turn, is extracted from WordNet. The rela-
tionship which needs to be proved between two con-
ON ONTOLOGY MATCHING PROBLEMS - FOR BUILDING A CORPORATE SEMANTIC WEB IN A
MULTI-COMMUNITIES ORGANIZATION
237

cepts is also converted to a propositional formula. SAT
solver will run on the set of calculated propositional
formulas to verify if the assumed relationship is true or
not. One of the main difficulties of this approach is the
choice of the best meaning of a term (a node) in the
graph from the lexical directory WordNet. By
consulting WordNet, a list of various meanings with
their set of synonyms is returned for a given term. The
question is that which meaning is the most adequate for
a term (a node) in the context where the node is placed
in the graph. SAT has not yet met this satisfactorily.
Our approach was motivated by some ideas of the
above approaches, and we study specially problems of
ontology matching. Unlike other approaches which use
only a part of available information, we try to use as
much as possible all of the information we have such as
ontology’s data instances, information about concepts,
relations, about structures of hierarchy of concepts
/relations… in the process of finding mappings. We
apply techniques for string comparison (e.g. Jaro-
Winkler metric), for calculating the similarity value
between descriptions of the concepts or of the relations
(TF/IDF scheme)… and we also integrate the WordNet
lexical database.
3 ONTOLOGY REPRESENTATION
There are many different definitions of ontology across
research fields. However, in the semantic web domain,
most approaches share the basic elements of ontology.
We adopt here the following definition of an
ontology and the meanings of its elements:
Ontology: an ontology is a conceptual vocabulary
shared by a community. It can be represented by a
hierarchy of concepts and a hierarchy of relations.
Class (also known as a concept): A class is a
representation for a conceptual grouping of similar
terms. For example, a
Vehicle could be represented
as a class which would have many subclasses such as
Car, Motorbike, etc.
Relation: A relation is used to describe a
relationship between two terms. The first term must be
a class that is the Domain of the relation and the second
must be a class that is the Range of the relation. For
example,
drive could be represented as a relation
such that its Domain is
Person and its Range is
Vehicle. A relation may have sub-relations. For
example,
firstName, lastName, title could be
sub-relations of the relation
designation.
Instance: An object is an instance of a class if it is a
member of the set denoted by that class. For example,
Mark could be an instance of class Person.
The relationship between a class and its subclasses,
or between a relation and its sub-relations is also called
an “is_a” relationship or a specialization relation. That
structures the set of classes as a hierarchy of classes
and the set of relations as a hierarchy of relations.
We formalize an ontology O as a tuple (Hc, Hr,
Domain, Range), where Hc is a set of classes, Hr is a
set of relations, Domain: Hr → Hc is a function which
returns the class that is the Domain of a relation, and
Range: Hr → Hc is a function which returns the class
that is the Range of a relation. Each class c is a tuple
(N, L, D), where N is its name (for identifying and
distinguishing a class from another), L is its set of
labels (a label provides a human-readable version of
the class name), and D is its set of descriptions (which
is used to provide a human-readable description of the
class). Similarly, a relation is defined as a tuple (N, L,
D).
Our formalization of ontology is very general, so
our proposed algorithm which uses that formalization
will work with most ontology representation languages.
In our experimentation, we evaluated our algorithm on
the RDF(S) formalism (Lassila and Swick 1999,
Brickley and Guha 2000). Our algorithm can be applied
on ontologies which are represented by the other
formalisms such as Description Logic, DAML+OIL…
The internal representation of an ontology in our
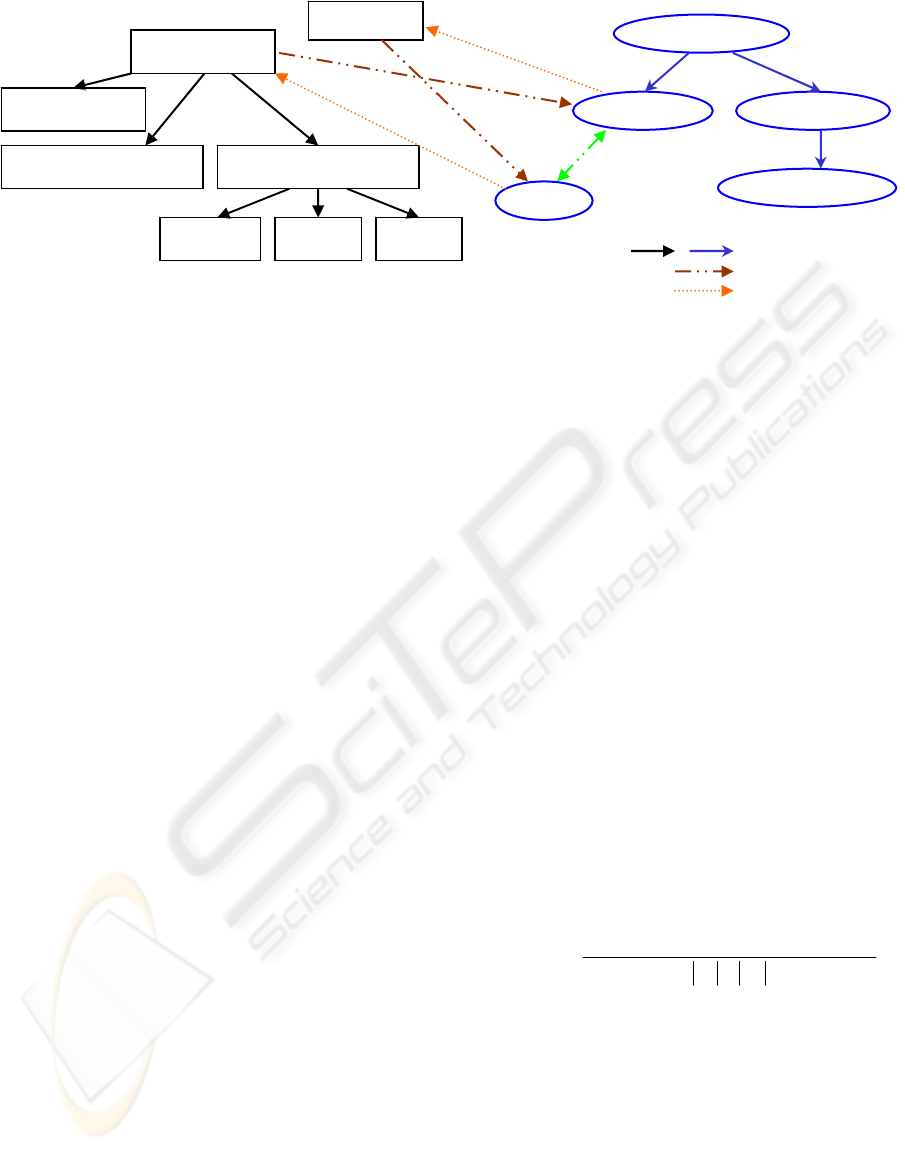
approach is a rooted directed acyclic graph (figure 1),
where classes and relations are nodes in the graph,
edges in the graph represent either the is_a relations
(i.e. a class or a relation is a specialization of its
parent), or domain or range relationship.
There will be a directed edge which connects from
a node A to a node B in the graph if one of the
following conditions are true: (i) node A represents a
class or a relation and node B represents its
specialization, (ii) node A represents the domain class
of the relation which is represented by node B, or (iii)
node A represents a relation and node B represents a
class in the range values of that relation.
4 ASCO ALGORITHM
The main idea behind our approach is to use maxi-
mally the available information which is contained in
the ontology in the progress of discovering the mapp-
ings between classes in the ontologies.
ICEIS 2004 - SOFTWARE AGENTS AND INTERNET COMPUTING
238

Author
All of the exploitable information in an ontology is
the information about the classes, the relations: their
names, their labels, their descriptions; the instances of
the classes or of the relations, the information about the
structure of the hierarchy of classes and of the
hierarchy of relations. By exploiting all of the available
information which we have, the calculation of the
similarity of classes (or relations) in the ontologies will
gain a better value. In our current work, we calculate
the similarity of two classes (or two relations) in two
ontologies by using the information about the names,
the labels, the descriptions of the classes (or the
relations). We plan to exploit the instances of classes
and relations, the facets, the structures of the ontologies
for calculating the similarity in our ongoing research.
The similarity of classes (or relations) will be
calculated by basing on the different information (e.g.
names, labels…), the obtained similarity results will be
combined to have the final similarity value. In our
current work, the information used for calculating the
similarity of two classes in two ontologies is similar to
information used for calculating the similarity of two
relations. So, from here, we will present the algorithm
that work on classes and find mappings of classes, the
algorithm for finding mappings of relations are
constructed similarly.
Our ASCO algorithm has two phases: a linguistic
phase and a structural phase.
4.1 Linguistic Matching
In this phase, the similarity of two classes in two
ontologies is calculated by relying on linguistic
components of their names, their labels and their
descriptions. For each of these three elements, a
similarity value is produced. A combination of these
values is a linguistic similarity value of the two
classes.
4.1.1 Name similarity calculation
Normally, the name of a class is a chain of characters, a
string, without blank characters (space). A name of
class may be a word, a term, or an expression (a
combination of words). This name is unique in the
ontology for identifying the class.
The similarity calculation of two names is carried
out in two steps: normalization and comparison.
The normalization step will normalize the name of
class to a set of tokens. A name will be tokenized
thanks to punctuation, upper case, special symbols,
digits… (e.g. SpatialEntity Æ {Spatial, Entity}). Then,
an expansion could be applied to the tokens:
abbreviations, acronyms are expanded (e.g. {SW} Æ
{Semantic, Web}).
Token similarity is calculated by using Jaro-
Winkler metric (JW), which is based on the number
and order of the common characters between two
strings.
Name similarity (NS) of two names N
1
and N
2
of
two classes A and B (each name is a set of tokens, N =
{n
i
}) is then the average of the best similarity of each
token with a token in the other set:
Instead of using Jaro-Winkler metric for calculating
string similarity between two tokens, we can apply the
other well-known metrics such as Levenstein, Monger-
Elkan (Cohen et al. 2003).
4.1.2 Label similarity calculation
Labels are also chains of characters. A label is used to
provide a human-readable version of the name of class.
),(),(
),(max),( where
),(),(
),(
21
21
1221
21
2211
NNNSBANS
nnJWNnMJW
NN
NnMJWNnMJW
NNNS
ji
Nn
i
NnNn
j
=
=
+
+
=
∈
∈∈
∑
∑
Document
GraphicDocument
Photo
SomeRelation
PlanSchema
Figure 1: An example of an ontology represented as a hierarchy of classes (a) and a hierarchy tions (b) of rela
(b)
CreatedBy
HasNumber
PhoneNumber
Create
inverseOf
(a)
File
TextualDocument
is_a (
domain
specialization)
range
ON ONTOLOGY MATCHING PROBLEMS - FOR BUILDING A CORPORATE SEMANTIC WEB IN A
MULTI-COMMUNITIES ORGANIZATION
239

So, the calculation of label similarity (LS) is somewhat
similar with the name similarity calculation. However,
there may be several labels L
i
for a name of class L =
{L
i
}. The label similarity calculation between two
classes of two ontologies is then extended to:
4.1.3 Description similarity calculation
A class may also have several comments (or
descriptions). These are descriptions for someone to
know about what that class is. They usually consist of a
long descriptive text. For that reason, using similarity
metrics such as Jaro, Smith-Waterman is not a good
choice. Instead, we applied the TF/IDF weighting
scheme, a well-known good method used in
information retrieval and classification domain, for
calculating the similarity between these descriptions.
In the original use of the TF/IDF weighting scheme
in information retrieval domain, TF/IDF ranking is
used for searches. It is a way of weighting the
relevance of a term to a document. For a vector search
in a set of documents for example, a document-vector
over all known terms is calculated for each document
with TF/IDF ranking. The correlations between these
vectors and a query-vector are then used to weight the
documents according to a query.
In our domain, we transformed and expressed this
problem as follows: we consider classes as documents.
The universe is the set of documents (set of classes)
which is built from all of classes in both of ontologies.
Words in the descriptions of a class are words in the
document representing that class. Each class will be
associated with a vector. The elements of these vectors
are calculated by basing on the contents of descriptions
in all of the classes (in both of two ontologies). Hence,
the similarity of two descriptions (one in the class A in
ontology O
1
and the other in the class B in ontology O
2
)
is the “distance” between two vectors which represent
class A and class B.
We will illustrate how we calculate these vectors
and the description similarity value.
Let v = (w
1
, w
2
, … w
S
) be a vector representing a
certain class c. S = |U| is number of distinct words in
the universe U of documents from two ontologies (a
document is built from all of the words in the descrip-
tions of a class). The i
th
element w
i
in the vector v,
which represents the class c in an ontology, is calcu-
lated as follow:
where tf
i
(term frequency) is the number of times
that the i
th
word in the universe U appears in the class
(document) c, idf
i
(inverse document frequency) is the
inverse of the percentage of the classes which contain
the word w
i
, N is the number of classes (documents) in
the universe U (which contains all of the classes in both
of two ontologies), n
i
is the number of classes which
contain the word w
i
at least one time.
),(),(
),(max),( where
),(),(
),(
21
21
1221
21
2211
LL
L
LL
LL
LL
L
LL
LSBALS
LLNSLMNS
LMNSLMNS
LS
ji
L
i
LL
j
=
=
+
+
=
∈
∈∈
∑∑
The similarity between two classes is therefore the
“distance” between two vectors that represent them.
Let v
i
= (w
i1
, w
i2
, …, w
iS
) and v
j
= (w
j1
, w
j2
, …, w
jS
) be
two vectors representing the class A of the first
ontology O
1
and the class B of the second ontology O
2
,
respectively. The similarity between A, B, named
DS(A, B) is defined as follows (cosine coefficient):
),(),(
)(*)(
),(
11
22
1
ji
S
k
S
k
jkik
S
k
jkik
ji
vvDSBADS
ww
ww
vvDS
=
=
∑∑
∑
==
=
As we have noticed, the descriptions usually
consist of a descriptive text. So, a pre-processing step is
necessary. This step will eliminate all of the stopwords
from the descriptions. Stopwords are words that carry
little useful information, such as the articles (the, a,
an…), the prepositions (to, of, in…), the conjunctions
(and, or…), pronouns (you, I…), modal verbs (are, is,
was…), … We can use a library of stopwords for this
step.
4.1.4 Combination of similarity values
Linguistic similarity (LingSim) is finally calculated
from above similarity values.
If this similarity value LingSim(A, B) exceeds a
threshold T
LingSim
> 0, we say that the class A of the
ontology O
1
is similar with the class B of the ontology
O
2
, or there is a mapping between class A and class B.
The best matching of class c
1i
in the ontology O
1
,
which is represented by the vector v
1i
, may be then
deduced:
where i=1..n, j=1..m, n, m are the number of classes
in the ontology O
1
and the ontology O
2
, respectively, c
2j
is a class in the ontology O
2
which is represented by the
vector v
2j
.
If LingSim(c
1
, c
2
) <= T
LingSim
, it means that there is
no similar class in the ontology O
2
with the class c
1
in
the ontology O
1
, otherwise there is a mapping between
c
1
and c
2
, called l-similar(c
1
,c
2
).
i
i
iii
n
N
idf
idftfw
2
log
*
=
=
1
*),(*),(
*),(),(
32
1
=
+
+
=
∑
i
i
w
wBADSwBALS
wBANSBA
TvvLingSim
vvLingSimvvLingSim
=
>
=
=
LingSim
),(),(
),(
),(max),(
maxmax
max
max
2121
21
21
..1
21
jiji
LingSimji
ji
mj
ji
vvLingSimccLingSim
⎪
⎨
⎩
⎪
⎧
ICEIS 2004 - SOFTWARE AGENTS AND INTERNET COMPUTING
240

4.1.5 WordNet integration
WordNet (Miller 1995) is a lexical reference system
whose design is inspired by current psycho-linguistic
theories of human lexical memory. English nouns,
verbs, adjectives and adverbs are organized into
synonym sets, each representing one underlying
concept. Different relations link the synonym sets.
There is also another system, named EuroWordNet
(EuroWordNet 1999), which is also a multilingual
database with wordnets for several European languages
(Dutch, Italian, Spanish, German, French, Czech and
Estonian). The wordnets are structured in the same way
as the WordNet for English.
Using these wordnets, we can find the synonyms of
a term. This helps to resolve the problems of term
conflicts, which are produced when the ontological
engineers design ontologies using terms differently. For
example, one can choose the term “person” for the
name of the class denoting an individual, another one
may decide to use the term “human” instead.
The synonyms are therefore helpful for comparing
and calculating the similarity value between names and
labels of classes.
Let synset(t) be the set of synonyms of the term t.
This set is obtained from consulting a wordnet library
such as WordNet or EuroWordNet. The formulas
calculating the similarity value NS, LS can then be
modified to newer versions:
and LS’ is calculated from NS’ instead of from NS:
The integration of WordNet in the calculation of
description similarity value may not be valuable and
cost the calculating time because the description is not
usually a term or a short expression. It contains itself
relatively enough information for being able to
compare to the others using the TF/IDF scheme.
4.2 Structural matching
In our current work, we extend the results of the work
of Dieng (Dieng & Hug 1998a, 1998b), that studied the
matching problems of two ontologies representing
through conceptual graph formalism, for structural
matching of ontologies.
4.2.1 Adjacency
We rely on the hypothesis that if the direct super-
concepts and/or the direct sub-concepts and/or the
sibling concepts of two concepts are already similar,
the two concepts in question may be also similar.
For i ∈ {1,2}, let c
i
be a concept in the hierarchy of
concepts Hc
i
. Let Pred(c
i
), Succ(c
i
), Sibl(c
i
) be respec-
tively the set of direct super-concepts of c
i
in Hc
i
, the
set of direct sub-concepts of c
i
in Hc
i
, and the set of
sibling concepts of c
i
in Hc
i
.
We define SameSet(S
1
,S
2
) is the set of elements in
S
1
which are similar with any element in S
2
. And
UnionSet(S
1
,S
2
), which is the set of all of elements in
S
1
combining with elements of S
2
that are not similar
with any element in S
1
.
SameSet(S
1
,S
2
)={s
i
∈S
1
; ∃s
j
∈S
2
:1-similar(s
i
,s
j
)}
UnionSet(S
1
,S
2
)=S
1
∪{s
i
∈S
2
;∀s
j
∈S
1
:¬1-similar(s
i
,s
j
)}
So, SamePred(c
i
,c
j
) = SameSet(Pred(c
i
), Pred(c
j
))
UnionPred(c
i
,c
j
) = UnionSet(Pred(c
i
), Pred(c
j
)).
We define P
Pred
, P
Succ
, P
Sibl
as the similar propor-
tions of the concepts in the sets Pred, Succ, Sibl,
respectively.
),('),('
)}(|{
),(max),( where
),(),(
),('
21
'
21
'
2
'
21
21
22
1
11
NNNSBANS
nsynsetnNnnNN
nnJWNnMJW
NN
NnMJWNnMJW
NNNS
jkijkii
ji
Nn
i
NnNn
j
=
∈∩∈∃∪=
=
+
+
=
∈
∈∈
∑∑
)c,c(edPrUnion
)c,c(edPrSame
)c,c(P
ji
ji
jiedPr
=
and the total similar proportion P
∑
∑
=
===
=
=
k
k
SiblSuccedPr
..k
kjikji
w
PP,PP,PP
w*)c,c(P)c,c(P
1
3
1
321
31
),('),('
),('max),(' where
),('),('
),('
21
21
1221
21
2211
LL
L
LL
LL
LL
L
LL
LSBALS
LLNSLMNS
LMNSLMNS
LS
ji
L
i
LL
j
=
=
+
+
=
∈
∈∈
∑∑
If the proportion P(c
i
,c
j
) exceeds the threshold T
P
,
two classes c
i
and c
j
are adjacent-structural similar.
4.2.2 Path of concepts
Our intuition is that if the path from the root of the first
hierarchy of concepts to the concept A contains similar
concepts with the path from the root to the concept B in
the second hierarchy of concepts, the two concepts A
and B may be similar too.
ON ONTOLOGY MATCHING PROBLEMS - FOR BUILDING A CORPORATE SEMANTIC WEB IN A
MULTI-COMMUNITIES ORGANIZATION
241

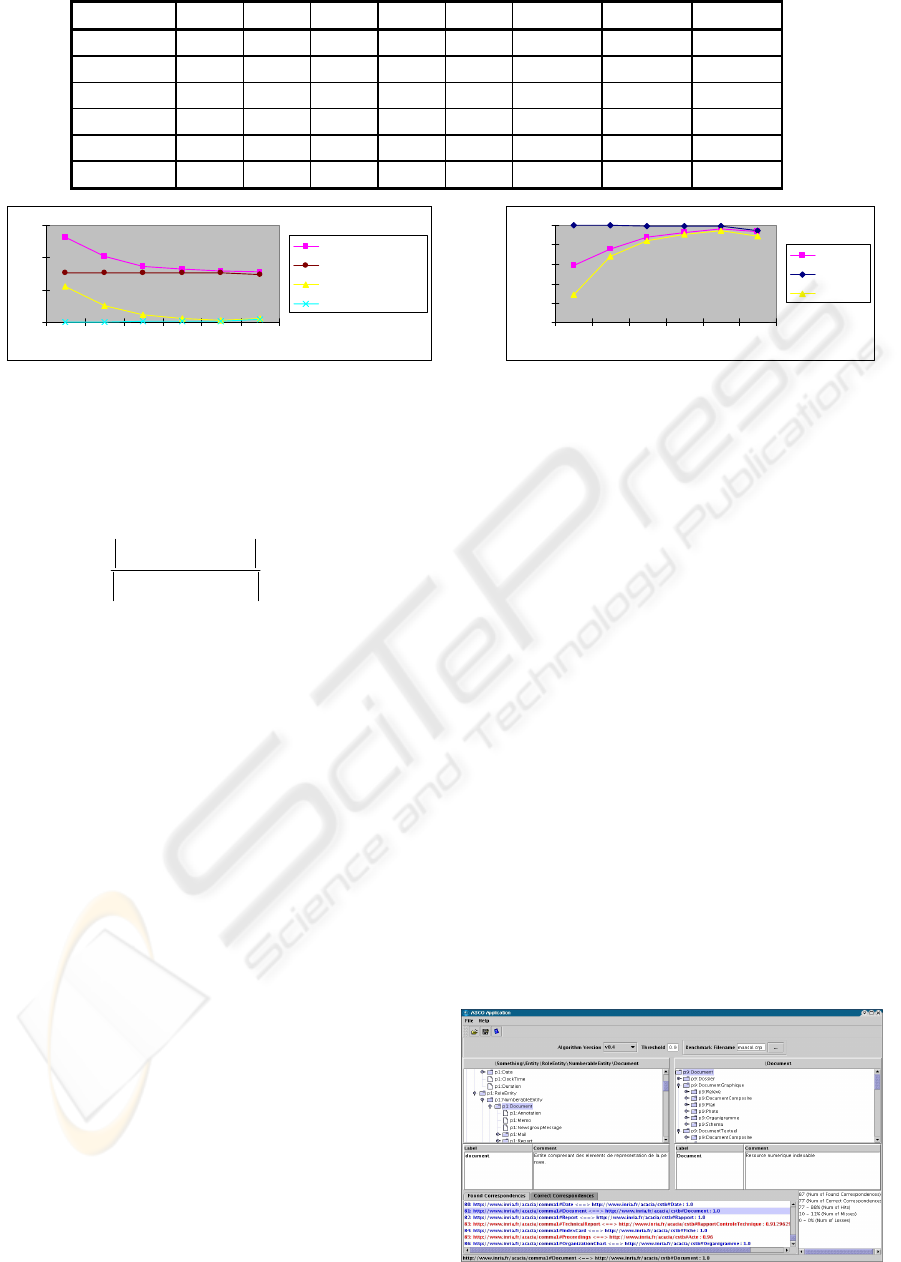
Threshold P R I F=P\I M=R\I Precision Recall Overall
0.85 132 77 77 55 0 0.583 1.000 0.286
0.87 102 77 77 25 0 0.755 1.000 0.675
0.90 87 77 76 11 1 0.874 0.987 0.844
0.95 82 77 76 6 1 0.927 0.987 0.909
0.98 79 77 76 3 1 0.962 0.987 0.948
1.00 78 77 73 5 4 0.936 0.948 0.883
0
50
100
150
0.85 0.87 0.90 0.95 0.98 1.00
P - Found matches
I - True positives
F - False positives
M - False negatives
0.000
0.200
0.400
0.600
0.800
1.000
0.85 0.87 0.90 0.95 0.98 1.00
Precision
Recall
Overall
Figure 2: ASCO results on two ontologies O’COMMA and O’Aprobatiom
Let Path(c
i
) be the path from the root to the class c
i
in the hierarchy Hc
i
. Path(c
i
) is a set of classes along
the path.
The similar proportion between two paths of two
classes c
i
and c
j
is
4.2.3 Combination of similarity values
Similarly with linguistic matching, structural mat-ching
results are combined to obtain the final structural
similarity value StrucSim.
4.3 Mapping generation
The output of ontology matching is a list of mappings
between the elements of the ontologies such as
concepts, relations. These mappings are generated by
relying on the final similarity value TotSim between
two elements, which is computed from linguistic and
structural similarity values LingSim and StrucSim. The
calculation of relation mappings is realized similarly.
If the TotSim of two elements A and B is higher
than a threshold T
accept
, we say that A is similar with B.
There may be several elements B
i
that are similar with
A. So, the algorithm ASCO can return correspondences
of 1:1 or 1:n cardinality.
5 EXPERIMENTAL RESULTS
The ASCO algorithm (figure 3) was implemented and
experimented with two real-world ontologies:
O’COMMA, which has 472 concepts and 77 relations;
and O’Aprobatiom, which has 460 concepts and 92
relations. O’COMMA is a corporate memory-dedicated
ontology, which was developed for the Comma
European IST project (2000-2001) (Gandon et al.
2002). O’Aprobatiom is an ontology for project in
building domain, developed through a cooperation
between our team and CSTB organization (CSTB). The
two ontologies were developed in two separate projects
by different persons, but they have some common
parts, therefore the obtained results (figure 2) are good.
We plan to experiment the ASCO algorithm on other
real-world ontologies, developed independently by
different teams in order to analyze the advantages and
the drawbacks of the algorithm.
))c(Path),c(Path(UnionSet)c,c(UnionPath
))c(Path),c(Path(SameSet)c,c(SamePath
)c,c(UnionPath
)c,c(SamePath
)c,c(P
jiji
jiji
ji
ji
jiPath
=
=
=
1
21
=
+=
∑
i
i
Path
w
w*)B,A(Pw*)B,A(P)B,A(StrucSim
In figure 2, P is the number of matches returned by
the algorithm, R is the number of manually determined
real matches, I is the number of true positives (i.e.
correctly identified matches), F = P\I is the number of
false positives (i.e. false matches), M is the number of
false negatives (i.e. missing matches), Precision = |I|/|P|
estimates the reliability of the match predictions, Recall
Figure 3: Interface of ASCO Application
ICEIS 2004 - SOFTWARE AGENTS AND INTERNET COMPUTING
242

= |I|/|R| specifies the share of real matches found, and
Overall = Recall * (2 – 1/Precision) represents a
combined measure for match quality (Melnik et al.
2002).
6 SUMMARY AND FUTURE
WORK
In this paper, we studied one of difficult problems in
the framework of knowledge management in an
heterogeneous organization. We argued that the mate-
rialization of the organizational memory in a “corporate
semantic web” requires to integrate the various
ontologies of the different groups of the organization.
Therefore, the task of matching ontologies for
supporting the integration, the exchange, the pro-
cessing of these heterogeneous data sources is crucial.
We presented our new algorithm, named ASCO,
for ontology matching. Our approach tries to use all
available information that we have about ontologies
such as data instances, concepts, relations, structures of
hierarchy of concepts/relations in the process of finding
mappings and we applied techniques such as Jaro-
Winkler metric, Monger-Elkan metric for string com-
parison, TF/IDF scheme, a well-known widely used
method used in the information retrieval and classifica-
tion fields, for calculating the similarity value between
descriptions of the concepts/relations, and we also
integrated WordNet, a lexical thesaurus system. We
believe that with our method, the obtained ontology
matching results will be more accurate and more
complete.
For further work, we plan to test widely the
algorithm ASCO on other real-world domains,
especially in medical domain, where there exists
several ontologies developed independently. Some
improvements in the structural phase of the algorithm
will also be studied (e.g. the application of the
information about the influence between the hierarchy
of concepts and the one of relations).
REFERENCES
Berners-Lee, T.; Hendler, J.; and Lassila O. 2001. The
Semantic Web, Scientific American.
Brickley, D. and Guha, R. 2000. Resource Description
Framework Schema Specification 1.0.
Cohen, W. W.; Ravikumar, P.; and Fienberg, S. 2003. A
Comparison of String Distance Metrics for Name-
Matching Tasks. IJCAI 2003, Workshop on
Information Integration on the Web.
Dieng, R. and Hug, S. 1998a. Comparison of "Personal
Ontologies" Represented through Conceptual Graphs.
In: Proc. of the 13th European Conference on Artifical
Intelligence (ECAI'98), p. 341-345, Brighton, UK.
Dieng, R. and Hug, S. 1998b. MULTIKAT, a Tool for
Comparing Knowledge from Multiple Experts. In
Proc. of the 6th Int. Conference on Conceptual
Structures (ICCS'98), Springer-Verlag, LNAI 1453.
Doan, A.; Domingos, P.; and Halevy, A. 2001.
Reconciling Schemas of Disparate Data Sources: A
Machine Learning Approach. In Proc. of the ACM
SIGMOD Conf. on Management of Data (SIGMOD-
2001).
Doan, A.; Madhavan, J.; Domingos, P.; and Halevy, A.
2002. Learning to Map between Ontologies on the
Semantic Web. The Eleventh International World
Wide Web Conference (WWW'2002), Hawaii, USA.
Gandon, F.; Dieng, R.; Corby, O.; and Giboin, A. 2002.
Semantic Web and Multi-Agents Approach to
Corporate Memory Management. In 17th IFIP World
Computer Congress. IIP Track-Intelligent Information
Processing, Eds Musen M., Neumann B., Studer R., p.
103-115. August 25-30, 2002, Montreal.
Giunchiglia, F. and Shvaiko P. 2003. Semantic Matching.
CEUR-WS, vol: 71.
Lassila, O. and Swick, R.R. 1999. Resource description
framework (RDF) Model and Syntax Specification.
W3C Recommendation, World Wide Web
Consortium, Cambridge (MA), February 1999.
Madhavan, J.; Bernstein, P. A.; and Rahm, E. 2001.
Generic Schema Matching with Cupid. In Proc. of the
27
th
Conference on Very Large Databases.
Mädche, A. and Staab, S. 2002. Measuring Similarity
between Ontologies. In Proc. Of the 13
th
Int.
Conference on Knowledge Engineering and
Management - EKAW-2002. Madrid, Spain.
Melnik, S.; Garcia-Molina, H.; and Rahm, E. 2001.
Similarity Flooding: A Versatile Graph Matching
Algorithm. Extended Technical Report,
http://dbpubs.stanford.edu/pub/2001- 25.
Melnik, S.; Garcia-Molina, H.; and Rahm, E. 2002.
Similarity Flooding: A Versatile Graph Matching
Algorithm and its Application to Schema Matching. In
Proc. 18th ICDE, San Jose CA.
Miller, G. A. 1995. WordNet: A lexical database for
English. Communications of the ACM, 38(11):39--41,
1995.
Noy, N. F. and Musen, M. A. 2001. Anchor-PROMPT:
Using Non-Local Context for Semantic Matching.
Workshop on Ontologies and Information Sharing.
IJCAI, Seattle, WA, . 2001.
Rahm, E. and Bernstein, P. A. 2001. A survey of
approaches to automatic schema matching. In The
VLDB Journal: Volume 10 Issue, pages 334-350.
Wache, H.; Vogele, T.; Visser, U.; Stuckenschmidt, H.;
Schuster, G.; Neumann H.; and Hubner, S. 2001.
Ontology-Based Integration of Information - A Survey
of Existing Approaches. Proceedings of the IJCAI-01
Workshop: Ontologies and Information Sharing.
EuroWordNet 1999. http://www.illc.uva.nl/EuroWordNet/
CSTB. Centre Scientifique et Technique du Bâtiment.
http://www.cstb.fr
ON ONTOLOGY MATCHING PROBLEMS - FOR BUILDING A CORPORATE SEMANTIC WEB IN A
MULTI-COMMUNITIES ORGANIZATION
243