
MEMORY MANAGEMENT FOR LARGE SCALE DATA STREAM
RECORDERS
∗
Kun Fu and Roger Zimmermann
Integrated Media System Center
University of Southern California
Los Angeles, California 90089
Keywords:
Memory management, real time, large-scale, continuous media, data streams, recording.
Abstract:
Presently, digital continuous media (CM) are well established as an integral part of many applications. In
recent years, a considerable amount of research has focused on the efficient retrieval of such media. Scant
attention has been paid to servers that can record such streams in real time. However, more and more devices
produce direct digital output streams. Hence, the need arises to capture and store these streams with an efficient
data stream recorder that can handle both recording and playback of many streams simultaneously and provide
a central repository for all data.
In this report we investigate memory management in the context of large scale data stream recorders. We are
especially interested in finding the minimal buffer space needed that still provides adequate resources with
varying workloads. We show that computing the minimal memory is an NP-complete problem and will
require further study to discover efficient heuristics.
1 INTRODUCTION
Digital continuous media (CM) are an integral part of
many new applications. Two of the main characteris-
tics of such media are that (1) they require real time
storage and retrieval, and (2) they require high band-
widths and space. Over the last decade, a considerable
amount of research has focused on the efficient re-
trieval of such media for many concurrent users (Sha-
habi et al., 2002). Algorithms to optimize such fun-
damental issues as data placement, disk scheduling,
admission control, transmission smoothing, etc., have
been reported in the literature.
Almost without exception these prior research ef-
forts assumed that the CM streams were readily avail-
able as files and could be loaded onto the servers off-
line without the real time constraints that the com-
plementary stream retrieval required. This is cer-
tainly a reasonable assumption for many applica-
tions where the multimedia streams are produced of-
fline (e.g., movies, commercials, educational lectures,
etc.). However, the current technological trends are
such that more and more sensor devices (e.g., cam-
∗
This research has been funded in part by NSF grants
EEC-9529152 (IMSC ERC) and IIS-0082826, and an unre-
stricted cash gift from the Lord Foundation.
eras) can directly produce digital data streams. Fur-
thermore, many of these new devices are network-
capable either via wired (SDI, Firewire) or wireless
(Bluetooth, IEEE 802.11x) connections. Hence, the
need arises to capture and store these streams with
an efficient data stream recorder that can handle both
recording and playback of many streams simultane-
ously and provide a central data repository.
The applications for such a recorder start at the
low end with small, personal systems. For exam-
ple, the “digital hub” in the living room envisioned
by several companies will in the future go beyond
recording and playing back a single stream as is cur-
rently done by TiVo and ReplayTV units (Wallich,
2002). Multiple camcorders, receivers, televisions,
and audio amplifiers will all connect to the digital
hub to either store or retrieve data streams. An exam-
ple for this convergence is the next generation of the
DVD specification that also calls for network access
of DVD players (Smith, 2003). At the higher end,
movie production will move to digital cameras and
storage devices. For example, George Lucas’ “Star
Wars: Episode II Attack of the Clones” was shot en-
tirely with high-definition digital cameras (Huffstut-
ter and Healey, 2002). Additionally, there are many
sensor networks that produce continuous streams of
54
Fu K. and Zimmermann R. (2004).
MEMORY MANAGEMENT FOR LARGE SCALE DATA STREAM RECORDERS.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 54-63
DOI: 10.5220/0002645400540063
Copyright
c
SciTePress
data. For example, NASA continuously receives data
from space probes. Earthquake and weather sensors
produce data streams as do web sites and telephone
systems.
In this paper we investigate issues related to mem-
ory management that need to be addressed for large
scale data stream recorders (Zimmermann et al.,
2003). After introducing some of the related work in
Section 2 we present a memory management model
in Section 3. We formalize the model and compute its
complexity in Section 4. We prove that because of a
combination of a large number of system parameters
and user service requirements the problem is expo-
nentially hard. Conclusions and future work are con-
tained in Section 5.
2 RELATED WORK
Managing the available main memory efficiently is
a crucial aspect of any multimedia streaming sys-
tem. A number of studies have investigated buffer
and cache management. These techniques can be
classified into three groups: (1) server buffer man-
agement (Makaroff and Ng, 1995; Shi and Ghande-
harizadeh, 1997; Tsai and Lee, 1998; Tsai and Lee,
1999; Lee et al., 2001), (2) network/proxy cache man-
agement (Sen et al., 1999; Ramesh et al., 2001; Chae
et al., 2002; Cui and Nahrstedt, 2003) and (3) client
buffer management (Shahabi and Alshayeji, 2000;
Waldvogel et al., 2003). Figure 1 illustrates where
memory resources are located in a distributed envi-
ronment.
In this report we aim to optimize the usage of server
buffers in a large scale data stream recording system.
This focus falls naturally into the first category clas-
sified above. To the best of our knowledge, no prior
work has investigated this issue in the context of the
design of a large scale, unified architecture, which
considers both retrieving and recording streams si-
multaneously.
3 MEMORY MANAGEMENT
OVERVIEW
A streaming media system requires main memory to
temporarily hold data items while they are transferred
between the network and the permanent disk storage.
For efficiency reasons, network packets are generally
much smaller than disk blocks. The assembly of in-
coming packets into data blocks and conversely the
partitioning of blocks into outgoing packets requires
main memory buffers. A widely used solution in
servers is double buffering. For example, one buffer
Table 1: Parameters for a current high performance com-
mercial disk drive.
Model ST336752LC
Series Cheetah X15
Manufacturer Seagate Technology, LLC
Capacity C 37 GB
Transfer rate R
D
See Figure 2
Spindle speed 15,000 rpm
Avg. rotational latency 2 msec
Worst case seek time ≈ 7 msec
Number of Zones Z 9
is filled with a data block that is coming from a disk
drive while the content of the second buffer is emp-
tied (i.e., streamed out) over the network. Once the
buffers are full/empty, their roles are reversed.
With a stream recorder, double buffering is still the
minimum that is required. With additional buffers
available, incoming data can be held in memory
longer and the deadline by which a data block must
be written to disk can be extended. This can reduce
disk contention and hence the probability of missed
deadlines (Aref et al., 1997). However, in our in-
vestigation we are foremost interested in the minimal
amount of memory that is necessary for a given work-
load and service level. Hence, we assume a double
buffering scheme as the basis for our analysis. In a
large scale stream recorder the number of streams to
be retrieved versus the number to be recorded may
vary significantly over time. Furthermore, the write
performance of a disk is usually significantly less than
its read bandwidth (see Figure 2b). Hence, these fac-
tors need to be considered and incorporated into the
memory model.
When designing an efficient memory buffer man-
agement module for a data stream recorder, one can
classify the interesting problems into two categories:
(1) resource configuration and (2) performance opti-
mization.
In the resource configuration category, a represen-
tative class of problems are: What is the minimum
memory or buffer size that is needed to satisfy certain
playback and recording service requirements? These
requirements depend on the higher level QoS require-
ments imposed by the end user or application envi-
ronment.
In the performance optimization category, a repre-
sentative class of problems are: Given certain amount
of memory or buffer, how to maximize our system per-
formance in terms of certain performance metrics?
Two typical performance metrics are as follows:
i Maximize the total number of supportable streams.
ii Maximize the disk I/O parallelism, i.e., minimize
the total number of parallel disk I/Os.
MEMORY MANAGEMENT FOR LARGE SCALE DATA STREAM RECORDERS
55

Content
Distribution
Network
Buffers
Streaming Server
Buffers
Dislay
Disks
Proxy Servers
Buffers
Camera
Clients
...
Figure 1: Buffer distribution in a traditional streaming system.
0
200000
400000
600000
800000
1000000
1200000
1400000
1600000
0
200
400
600
800
1000
1200
1400
Movie consumption rate
Data Rate [bytes/sec]
Time [seconds]
0
10
20
30
40
50
60
0 5 10 15 20 25 30
Transfer Rate (MB/s)
Disk Capacity (GB)
read avg.
write avg.
Figure 2a: The consumption rate of a movie encoded
with a VBR MPEG-2 algorithm (“Twister”).
Figure 2b: Maximum read and write rate in different
areas (also called zones) of the disk. The transfer rate
varies in different zones.i The write bandwidth is up to
30% less than the read bandwidth.
Figure 2: Variable bit rate (VBR) movie characteristics and Disk characteristics of a high performance disk drive (Seagate
Cheetah X15, see Table 1).
We focus on the resource configuration problem in
this report, since it is a prerequisite to optimizing per-
formance.
4 MINIMIZING THE SERVER
BUFFER SIZE
Informally, we are investigating the following ques-
tion: What is the minimum memory buffer size S
buf
min
that is needed to satisfy a set of given streaming and
recording service requirements?
In other words, the minimum buffer size must sat-
isfy the maximum buffer resource requirement under
the given service requirements. We term this prob-
lem the Minimum Server Buffer or MSB. We illus-
trate our discussion with the example design of a
large scale recording system called HYDRA, a High-
performance Data Recording Architecture (Zimmer-
mann et al., 2003). Figure 3 shows the overall archi-
tecture of HYDRA. The design is based on random
data placement and deadline driven disk scheduling
techniques to provide high performance. As a result,
statistical rather than deterministic service guarantees
are provided.
The MSB problem is challenging because the me-
dia server design is expected to:
i support multiple simultaneous streams with differ-
ent bandwidths and variable bit rates (VBR) (Fig-
ure 2a illustrates the variability of a sample MPEG-
2 movie). Note that different recording devices
might also generate streams with variable band-
width requirements.
ii support concurrent reading and writing of streams.
The issue that poses a serious challenge is that disk
drives generally provide considerably less write
than read bandwidth (see Figure 2b).
iii support multi-zoned disks. Figure 2b illustrates
how the disk transfer rates of current generation
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
56
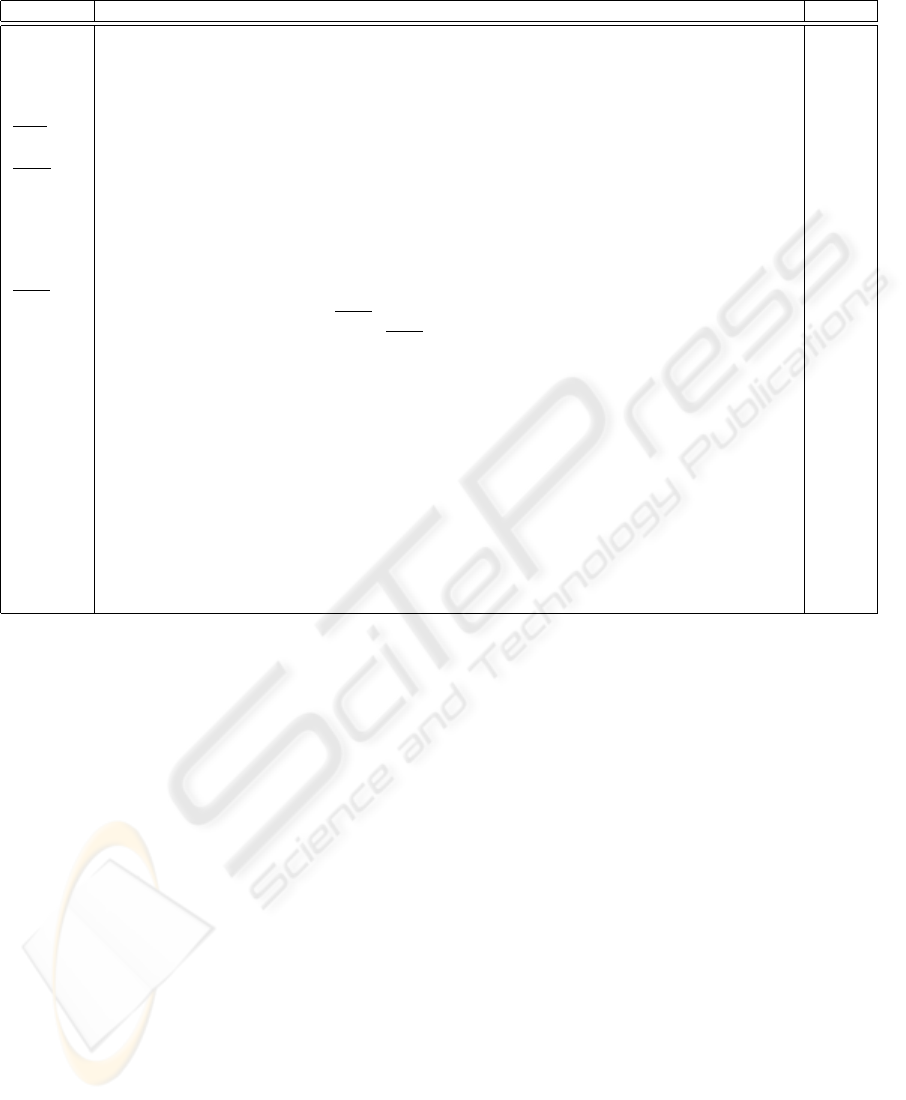
Table 2: List of terms used repeatedly in this study and their respective definitions.
Term Definition Units
B
disk
Block size on disk MB
T
svr
Server observation time interval second
ξ The number of disks in the system
n The number of concurrent streams
p
iodisk
Probability of missed deadline by reading or writing
R
Dr
Average disk read bandwidth during T
svr
(no bandwidth allocation for writing) MB/s
p
req
The threshold of probability of missed deadline, it is the worse situation that client can endure.
R
Dw
Average disk write bandwidth during T
svr
(no bandwidth allocation for reading) MB/s
t
seek
(j) Seek time for disk access j, where j is an index for each disk access during a T
svr
ms
R
Dr
(j) Disk read bandwidth for disk access j (no bandwidth allocation for writing) MB/s
µ
t
seek
(j) Mean value of random variable t
seek
(j), where j is an index for each disk access during a T
svr
ms
σ
t
seek
(j) Standard deviation of random variable t
seek
(j) ms
β Relationship factor between R
Dr
and R
Dw
t
seek
The average disk seek time during T
svr
ms
µ
t
seek
Mean value of random variable t
seek
ms
σ
t
seek
Standard deviation of random variable t
seek
ms
α Mixed-load factor, the percentage of reading load in the system
m
1
The number of movies existed in HYDRA
D
rs
i
The amount of data that movie i is consumed during T
svr
MB
µ
rs
i
Mean value of random variable D
rs
i
MB
σ
rs
i
Standard deviation of random D
rs
i
MB
n
rs
i
The number of retrieving streams for movie i
m
2
The number of different recording devices
D
ws
i
The amount of data that is generated by recording device i during T
svr
µ
ws
i
Mean value of random variable D
ws
i
MB
σ
ws
i
Standard deviation of random D
ws
i
MB
n
ws
i
The number of recording streams by recording device i
N
max
The maximum number of streams supported in the system
S
buf
min
The minimum buffer size needed in the system MB
drives is platter location dependent. The outermost
zone provides up to 30% more bandwidth than the
innermost one.
iv support flexible service requirements (see Sec-
tion 4.1 for details), which should be configurable
by Video-on-Demand (VOD) service providers
based on their application and customer require-
ments.
As discussed in Section 3, a double buffering
scheme is employed in HYDRA. Therefore, two
buffers are necessary for each stream serviced by the
system. Before formally defining the MSB problem,
we outline our framework for service requirements in
the next section. Table 4 lists all the parameters and
their definitions used in this paper.
4.1 Service Requirements
Why do we need to consider service requirements in
our system? We illustrate and answer this question
with an example.
Assume that a VOD system is deployed in a five-
star hotel, which has 10 superior deluxe rooms, 20
deluxe rooms and 50 regular rooms. There are 30
movies stored in the system, among which five are
new releases that started to be shown in theaters dur-
ing the last week. Now consider the following sce-
nario. The VOD system operator wants to configure
the system so that (1) the customers who stay in su-
perior deluxe rooms should be able to view any one
of the 30 movies whenever they want, (2) those cus-
tomers that stay in deluxe rooms should be able to
watch any of the five new movies released recently at
anytime, and finally (3) the customers in the regular
rooms can watch movies whenever system resources
permit.
The rules and requirements described above are
formally a set of service constraints that the VOD
operator would like to enforce in the system. We
term these type of service constraints service require-
ments. Such service requirements can be enforced
in the VOD system via an admission control mech-
anism. Most importantly, these service requirements
will affect the server buffer requirement. Next, we
will describe how to formalize the memory configu-
ration problem and find the minimal buffer size in a
streaming media system.
MEMORY MANAGEMENT FOR LARGE SCALE DATA STREAM RECORDERS
57

Admission Control
Node Coordination
Mem. Mgmt
Scheduler
Mem. Mgmt
Scheduler
Mem. Mgmt
Scheduler
LAN Environment
Data sources produce packetized realtime data streams (e.g., RTP)
Camera
Microphone
Haptic
Sensor
Internet (WAN)
Packets
Packets
(e.g., RTP)
Node 0 Node 1 Node N
Data Stream Recorder
Display /
Renderer
Recording
Playback
AggregationAggregation Aggregation
(Data is transmitted directly
from every node)
B2 B0 B6 B3
B7
B1B5
B4
Packet Router
E.g., DV Camcorder
Figure 3: HYDRA: Data Stream Recorder Architecture.
Multiple source and rendering devices are interconnected
via an IP infrastructure. The recorder functions as a data
repository that receives and plays back many streams con-
currently.
4.2 MSB Problem Formulation
4.2.1 Stream Characteristics and
Load Modeling
Given a specific time instant, there are m
1
movies
loaded in the HYDRA system. Thus, these m
1
movies are available for playback services. The HY-
DRA system activity is observed periodically, during
a time interval T
svr
. Each movie follows an inher-
ent bandwidth consumption schedule due to its com-
pression and encoding format, as well as its specific
content characteristics. Let D
rs
i
denote the amount of
data that movie i is consuming during T
svr
. Further-
more, let µ
rs
i
and σ
rs
i
denote the mean and standard
deviation of D
rs
i
, and let n
rs
i
represent the number of
retrieval streams for movie i.
We assume that there exist m
2
different recording
devices which are connected to the HYDRA system.
These recording devices could be DV camcorders,
microphones or haptic sensors as shown in Figure 3.
Therefore, in terms of bandwidth characteristics, m
2
types of recording streams must be supported by the
recording services in the HYDRA system. Analogous
with the retrieval services, D
ws
i
denotes the amount
of data that is generated by recording device i during
time interval T
svr
. Let µ
ws
i
and σ
ws
i
denote the mean
and standard deviation of D
ws
i
and let n
ws
i
represent
the number of recording streams generated by record-
ing device i. Consequently, we can compute the total
number of concurrent streams n as
n =
m
1
i=1
n
rs
i
+
m
2
i=1
n
ws
i
(1)
Thus, the problem that needs to be solved
translates to finding the combination of
<n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
>, which maximizes
n. Hence, N
max
can be computed as
N
max
= max(n)=max(
m
1
i=1
n
rs
i
+
m
2
i=1
n
ws
i
) (2)
under some service requirements described below.
Note that if the double buffering technique is em-
ployed, and after computing N
max
, we can easily ob-
tain the minimum buffer size S
buf
min
as
S
buf
min
=2B
disk
N
max
(3)
where B
disk
is the data block size on the disks. Note
that in the above computation we are considering the
worst case scenario where no two data streams are
sharing any buffers in memory.
4.2.2 Service Requirements Model-
ing
We start by assuming the example described in Sec-
tion 4.1 and following the notation in the previous
section. Thus, let n
rs
1
, ..., n
rs
30
denote the number of
retrieval streams corresponding to the 30 movies in
the system. Furthermore, without loss of generality,
we can choose n
rs
1
, ..., n
rs
5
as the five newly released
movies.
To enforce the service requirements, the operator
must define the following constraints for each of the
corresponding service requirements:
C1: n
rs
1
, ..., n
rs
30
≥ 10.
C2: n
rs
1
, ..., n
rs
5
≥ 20.
Note that we do not define the constraint for the third
service requirement because it can be automatically
supported by the statistical admission model defined
in the next section.
The above constraints are equivalent to the follow-
ing linear constraints:
C1: n
rs
1
, ..., n
rs
5
≥ 30.
C2: n
rs
6
, ..., n
rs
30
≥ 10.
These linear constraints can be generalized into the
following linear equations:
m
1
j=1
a
rs
ij
n
rs
j
+
m
2
k=1
a
ws
ik
n
ws
k
≤ b
i
n
rs
j
≥ 0
n
ws
k
≥ 0
n
rs
j
and n
ws
k
are integers
(4)
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
58

where i ∈ [0,w], w is the total number of linear con-
straints, j ∈ [1,m
1
], k ∈ [1,m
2
], and a
rs
ij
, a
ws
ik
, b
i
are
linear constraint parameters.
4.2.3 Statistical Service Guarantee
To ensure high resource utilization in HYDRA, we
provide statistical service guarantees to end users
through a comprehensive three random variable
(3RV) admission control model. The parameters in-
corporated into the random variables are the variable
bit rate characteristic of different retrieval and record-
ing streams, a realistic disk model that considers the
variable transfer rates of multi-zoned disks, variable
seek and rotational latencies, and unequal reading and
recording data rate limits.
Recall that system activity is observed periodically
with a time interval T
svr
. Formally, our 3RV model
is characterized by the following three random vari-
ables: (1)
m
1
i=1
n
rs
i
D
rs
i
+
m
2
i=1
n
ws
i
D
ws
i
, denoting
the amount of data to be retrieved or recorded dur-
ing T
svr
in the system, (2) t
seek
, denoting the aver-
age disk seek time during each observation time in-
terval T
svr
, and (3) R
Dr
denoting the average disk
read bandwidth during T
svr
.
We assume that there are ξ disks present in the
system and that p
iodisk
denotes the probability of
a missed deadline when reading or writing, com-
puted with our 3RV model. Furthermore, the statis-
tical service requirements are characterized by p
req
:
the threshold of the highest probability of a missed
deadline that a client is willing to accept (for details
see (Zimmermann and Fu, 2003)).
Given the above introduced three random variables
— abbreviated as X, Y and Z — the probability of
missed deadlines p
iodisk
can then be evaluated as fol-
lows
p
iodisk
= P [(X, Y, Z) ∈]
=
f
X
(x)f
Y
(y)f
Z
(z)dxdydz
≤ p
req
(5)
where is computed as
=
(X, Y, Z) |
X
ξ
>
(αZ+(1−α)βZ)×T
svr
1+
Y ×(αZ+(1−α)βZ)
B
disk
(6)
In Equation 6, B
disk
denotes the data block size on
disk, α is the mixload factor, which is the percent-
age of reading load in the system and is computed
by Equation 10, and β is the relationship factor be-
tween the read and write data bandwidth. The neces-
sary probability density functions f
X
(x), f
Y
(y), and
f
Z
(z) can be computed as
f
X
(x)
=
e
−
[
x−(
m1
i=1
n
rs
i
µ
rs
i
+
m2
i=1
n
ws
i
µ
ws
i
)
]
2
2×(
m1
i=1
n
rs
i
(σ
rs
i
)
2
+
m2
i=1
n
ws
i
(σ
ws
i
)
2
)
√
2π(
m1
i=1
n
rs
i
(σ
rs
i
)
2
+
m2
i=1
n
ws
i
(σ
ws
i
)
2
)
(7)
while f
Y
(y) similarly evaluates to
f
Y
(y)
≈
e
−
(
m1
i=1
n
rs
i
µ
rs
i
+
m2
i=1
n
ws
i
µ
ws
i
)
2B
disk
y−µ
t
seek
(j)
σ
t
seek
(j)
2
2πσ
2
t
seek
(j)
(8)
with µ
t
seek
(j) and σ
t
seek
being the mean value
and the standard deviation of the random variable
t
seek
(j), which is the seek time
2
for disk access j,
where j is an index for each disk access during T
svr
.
Finally, f
Z
(z) can be computed as
f
Z
(z)
≈
e
−
(
m1
i=1
n
rs
i
µ
rs
i
+
m2
i=1
n
ws
i
µ
ws
i
)
2B
disk
z−µ
R
Dr
(j)
σ
R
Dr
(j)
2
2πσ
2
R
Dr
(j)
(9)
where µ
R
Dr
(j) and σ
R
Dr
(j) denote the mean value
and standard deviation for random variable R
Dr
(j).
This parameter represents the disk read bandwidth
limit for disk access j, where j is an index for each
disk access during a T
svr
, and α can be computed as
α ≈
m1
i=1
n
rs
i
µ
rs
i
m1
i=1
n
rs
i
µ
rs
i
+
m2
i=1
n
ws
i
µ
ws
i
β
(10)
We have now formalized the MSB problem. Our
next challenge is to find an efficient solution. How-
ever, after some careful study we found that there are
two properties — integer constraints and linear equa-
tion constraints — that make it hard to solve. In fact,
MSB is a NP-complete problem. We will prove it
formally in the next section.
4.3 NP-Completeness
To show that MSB is NP-complete, we first need to
prove that MSB ∈NP.
Lemma 4.1: MSB ∈NP
Proof: We prove this lemma by providing a
polynomial-time algorithm, which can verify MSB
with a given solution {n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
}.
We have constructed an algorithm called Check-
Optimal, shown in Figure 4. Given a set
{n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
}, the algorithm CheckOp-
timal can verify the MSB in polynomial-time for the
following reasons:
2
t
seek
(j) includes rotational latency as well.
MEMORY MANAGEMENT FOR LARGE SCALE DATA STREAM RECORDERS
59

Procedure CheckOptimal (n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
)
/* Return TRUE if the given solution satisfies */
/* all the constraints and maximize n,*/
/* otherwise, return FALSE. */
(i) S={n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
},
If CheckConstraint(S)==TRUE
Then continue;
Else return FALSE;
(ii) For (i =1; i ≤ m
1
; i ++)
{
S
= S; S
.n
rs
i
= S
.n
rs
i
+1;
If CheckConstraint(S
)==TRUE
Then return FALSE;
Else continue;
}
(iii) For (i =1; i ≤ m
2
; i ++)
{
S
= S; S
.n
ws
i
= S
.n
ws
i
+1;
If CheckConstraint(S
)==TRUE
Then return FALSE;
Else continue;
}
(iv).return TRUE;
end CheckOptimal;
Procedure CheckConstraint (n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
)
/* Return TRUE if the given solution satisfies */
/* all the constraints, otherwise return FALSE. */
(i) S={n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
},
If S satisfies all the linear constraints defined
in Equation 4.
Then continue;
Else return FALSE;
(ii) If S satisfies the statistical service guarantee
defined in Equation 5.
Then return TRUE;
Else return FALSE;
end CheckConstraint;
Figure 4: An algorithm to check if a given solution
{n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
} satisfies all the constraints
specified in Equation 4 and 5 and maximizes n as well.
1 Procedure CheckConstraint runs in polynomial
time because both step (i) and step (ii) run in poly-
nomial time. Note that the complexity analysis of
step (ii) is described in details elsewhere (Zimmer-
mann and Fu, 2003).
2 Based on the above reasoning, we conclude that
procedure CheckOptimal runs in polynomial time
because each of its four component steps runs in
polynomial time.
Therefore, MSB ∈NP.
Next, we show that MSB is NP-hard. To accom-
plish this we first define a restricted version of MSB,
termed RMSB.
Definition 4.2 : The Restricted Minimum Server
Buffer Problem (RMSB) is identical to MSB except
that p
req
=1.
Subsequently, RMSB can be shown to be NP-
hard by reduction from Integer Linear Programming
(ILP) (Papadimitriou and Steiglitz, 1982).
Definition 4.3 : The Integer Linear Programming
(ILP) problem:
Maximize
n
i=1
C
j
X
j
subject to
n
i=1
a
ij
X
j
≤ b
i
for i =1, 2,...,m, and
X
j
≥ 0 and X
j
is integer for j =1, 2,...,n.
Theorem 4.4: RMSB is NP-hard.
Proof: We use a reduction from ILP. Recall that
in MSB, Equation 5 computes the probability of
a missed deadline during disk reading or writing
p
iodisk
, and p
iodisk
is required to be less than or
equal to p
req
. Recall that in RMSB, p
req
=1.
Therefore, it is obvious that p
iodisk
≤ (p
req
=1)
is always true no matter how the combination of
{n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
} is selected. Therefore, in
RMSB, the constraint of statistical service guarantee
could be removed, which then transforms RMSB into
an ILP problem.
Theorem 4.5: MSB is NP-hard.
Proof: By restriction (Garey and Johnson, 1979), we
limit MSB to RMSB by assuming p
req
=1.Asa
result – based on Theorem 4.4 – MSB is NP-hard.
Theorem 4.6: MSB is NP-complete.
Proof: It follows from Lemma 4.1 and Theorem 4.5
that MSB is NP-complete.
4.4 Algorithm to Solve MSB
Figure 5 illustrates the process of solving the MSB
problem. Four major parameter components are uti-
lized in the process: (1) Movie Parameters (see Sec-
tion 4.2.1), (2) Recording Devices (see Section 4.2.1),
(3) Service Requirements (see Section 4.2.2), and (4)
Disk Parameters (for details see (Zimmermann and
Fu, 2003)). Additionally, there are four major compu-
tation components involved in the process: (1) Load
Space Navigation, (2) Linear Constraints Checking,
(3) Statistical Admission Control, and (4) Minimum
Buffer Size Computation.
The Load Space Navigator checks
through each of the possible combinations
{n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
} in the search space.
It also computes the temporary maximum stream
number N
max
when it receives the results from the
admission control module. Each of the possible
solutions {n
rs
1
...n
rs
m
1
,n
ws
1
...n
ws
m
2
} is first checked
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
60

Statistical
Admission
Control Compute
Minimum
Buffer Size
Disks Parameters
...
...
Recording Devices
Movies Parameters
...
Load Space
Navigator
Linear
Constraints
Checking
Service
Requirements
Compute the maximum
number of streams N
max
Nmax
Figure 5: Process to solve the MSB problem.
by the Linear Constraints Checking module, which
enforces the service requirements formulated in
Section 4.2.2. The solutions that satisfy the service
requirements will be further verified by the Statistical
Admission Control module described in Section 4.2.3,
which provides the statistical service guarantees for
the recording system. After exhausting the search
space, the load space navigator forwards the highest
N
max
to the Minimum Buffer Size Computation
module, which computes the minimal buffer size
S
buf
min
.
We conclude by providing an algorithm that solves
the MSB problem in exponential time shown in Fig-
ure 6, based on the process illustrated in Figure 5.
5 CONCLUSIONS AND FUTURE
RESEARCH DIRECTIONS
We have presented a novel buffer minimization prob-
lem (MSB) motivated by the design of our large scale
data stream recording system HYDRA. We formally
proved that MSB is NP-complete, and we also pro-
vided an initial exponential-time algorithm to solve
the problem. As part of our future work, we will focus
on finding an approximation algorithm which solves
the MSB problem in polynomial-time. Furthermore,
we plan to evaluate the memory management mod-
ule in the context of the other system components
that manage data placement, disk scheduling, block
prefetching and replacement policy, and QoS require-
ments. Finally, we plan to implement and evaluate the
memory management module in our HYDRA proto-
type system.
REFERENCES
Aref, W., Kamel, I., Niranjan, T. N., and Ghandeharizadeh,
S. (1997). Disk Scheduling for Displaying and
Recording Video in Non-Linear News Editing Sys-
tems. In Proceedings of the Multimedia Comput-
ing and Networking Conference, pages 228–239, San
Jose, California. SPIE Proceedings Series, Volume
3020.
Chae, Y., Guo, K., Buddhikot, M. M., Suri, S., and Ze-
gura, E. W. (2002). Silo, rainbow, and caching token:
Schemes for scalable, fault tolerant stream caching.
Special Issue of IEEE Journal of Selected Area in
Communications on Internet Proxy Services.
Cui, Y. and Nahrstedt, K. (2003). Proxy-based asyn-
chronous multicast for efficient on-demand media
distribution. In The SPIE Conference on Multime-
dia Computing and Networking 2003 (MMCN 2003),
Santa Clara, California, pages 162–176.
Garey, M. R. and Johnson, D. S. (1979). Computers and In-
tractability: A Guide to Theory of NP-Completeness.
W.H.Freeman and Company, New York.
Huffstutter, P. J. and Healey, J. (2002). Filming Without the
Film. Los Angeles Times, page A.1.
Lee, S.-H., Whang, K.-Y., Moon, Y.-S., and Song, I.-
Y. (2001). Dynamic Buffer Allocation in Video-
On-Demand Systems. In Proceedings of the inter-
national conference on Management of data (ACM
SIGMOD’2001), Santa Barbara, California, United
States, pages 343–354.
Makaroff, D. J. and Ng, R. T. (1995). Schemes for Im-
plementing Buffer Sharing in Continuous-Media Sys-
tems. Information Systems, Vol. 20, No. 6., pages 445–
464.
Papadimitriou, C. H. and Steiglitz, K. (1982). Combinato-
rial Optimization: Algorithms and Complexity. Pren-
tice Hall, Inc., Englewood Cliffs, New Jersey 07632.
Ramesh, S., Rhee, I., and Guo, K. (2001). Multicast with
cache (mcache): An adaptive zero delay video-on-
demand service. In IEEE INFOCOM ’01, pages 85–
94.
Sen, S., Rexford, J., and Towsley, D. F. (1999). Proxy prefix
caching for multimedia streams. In IEEE INFOCOM
’99, pages 1310–1319.
MEMORY MANAGEMENT FOR LARGE SCALE DATA STREAM RECORDERS
61

Shahabi, C. and Alshayeji, M. (2000). Super-streaming:
A new object delivery paradigm for continuous me-
dia servers. Journal of Multimedia Tools and Applica-
tions, 11(1).
Shahabi, C., Zimmermann, R., Fu, K., and Yao, S.-Y. D.
(2002). Yima: A Second Generation Continuous Me-
dia Server. IEEE Computer, 35(6):56–64.
Shi, W. and Ghandeharizadeh, S. (1997). Buffer Sharing
in Video-On-Demand Servers. SIGMETRICS Perfor-
mance Evaluation Review, 25(2):13–20.
Smith, T. (2003). Next DVD spec. to offer Net access not
more capacity. The Register.
Tsai, W.-J. and Lee, S.-Y. (1998). Dynamic Buffer Manage-
ment for Near Video-On-Demand Systems. Multime-
dia Tools and Applications, Volume 6, Issue 1, pages
61–83.
Tsai, W.-J. and Lee, S.-Y. (1999). Buffer-Sharing Tech-
niques in Service-Guaranteed Video Servers. Mul-
timedia Tools and Applications, Volume 9, Issue 2,
pages 121–145.
Waldvogel, M., Deng, W., and Janakiraman, R. (2003).
Efficient buffer management for scalable media-on-
demand. In The SPIE Conference on Multime-
dia Computing and Networking 2003 (MMCN 2003),
Santa Clara, California.
Wallich, P. (2002). Digital Hubbub. IEEE Spectrum,
39(7):26–29.
Zimmermann, R. and Fu, K. (2003). Comprehensive Statis-
tical Admission Control for Streaming Media Servers.
In Proceedings of the 11th ACM International Multi-
media Conference (ACM Multimedia 2003), Berkeley,
California.
Zimmermann, R., Fu, K., and Ku, W.-S. (2003). Design of
a large scale data stream recorder. In The 5th Interna-
tional Conference on Enterprise Information Systems
(ICEIS 2003), Angers - France.
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
62

Procedure FindMSB
/* Return the minimum buffer size */
(i) N
max
= FindNmax; /* Find the maximum number of supportable streams */
(ii) Compute S
buf
min
using Equation 3.
(iii) return S
buf
min
;
end FindMSB;
Procedure FindNmax
/* Return the maximum number of supportable streams */
(i) Considering only statistical service guarantee p
req
, let N
rs
i
denote the maximum of supportable
retrieving streams of movie i without any other system load. Find the N
rs
i
, where i ∈ [1,m
1
].
(ii) Considering only statistical service guarantee p
req
, let N
ws
i
denote the maximum of supportable
recording streams of generated by recording device i without any other system load.
Find the N
ws
i
, where i ∈ [1,m
2
].
(iii) N
curmax
=0; S
curmax
={0 ...0, 0 ...0}
(iv) For (X
rs
1
=1; X
rs
1
≤ N
rs
1
; X
rs
1
++)
......
For (X
rs
m
1
=1; X
rs
m
1
≤ N
rs
m
1
; X
rs
m
1
++)
For (X
ws
1
=1; X
ws
1
≤ N
ws
1
; X
ws
1
++)
......
For (X
ws
m
2
=1; X
ws
m
2
≤ N
ws
m
2
; X
ws
m
2
++)
{
S
= {X
rs
1
...X
rs
m
1
,X
ws
1
...X
ws
m
2
};
If CheckConstraint(S
) == TRUE /* CheckConstraint is defined in Figure 4 */
Then
{
If
m
1
i=1
X
rs
i
+
m
2
i=1
X
ws
i
>N
curmax
Then
N
curmax
=
m
1
i=1
X
rs
i
+
m
2
i=1
X
ws
i
; S
curmax
={X
rs
1
...X
rs
m
1
,X
ws
1
...X
ws
m
2
}
}
}
(v) return N
curmax
;
end FindNmax;
Figure 6: Algorithm to solve MSB problem.
MEMORY MANAGEMENT FOR LARGE SCALE DATA STREAM RECORDERS
63
