DESIGN AND IMPLEMENTATION OF A SCALABLE

FUZZY CASE-BASED MATCHING ENGINE

RAMI HANSENNE, JONAS VAN POUCKE, VEERLE VAN DER SLUYS

Actonomy NV, Stapelplein 70, B – 9000 GENT (Belgium)

BARTEL VAN DE WALLE

Department of Information Systems and Management, Tilburg University

eywords: Case-based reasoning; fuzzy set theory; matching engine; matching techniques.

Abstract: We discuss the design and the implementation of a flexible and scalable fuzzy case-based matching engine.

The engine’s flexible design is illustrated for two of its core components: the internal representation of cases

by means of a variety of crisp and fuzzy data types, and the fuzzy operations to execute the ensuing case

matching process. We investigate the scalability of the matching engine by a series of benchmark tests of

increasing complexity, and find that the matching engine can manage an increasingly heavy load. This

indicates that the engine can be used for demanding matching processes. We conclude by pointing at several

applications in experimental electronic markets for which the matching engine currently is being put to use,

and indicate avenues for future research.

1 INTRODUCTION

Case-based reasoning (CBR) is a problem solving

approach resembling an example-based search

process. Problems that have been encountered earlier

are stored as examples, and when confronted with a

new problem, similar problems from this set are

identified by means of a search process. The query

(or target) problem is then classified according to the

similarity of earlier examples that have been

identified (Kolodner, 1993). More formally, CBR

can be defined as a four-step process (Aamodt and

Plaza, 1994):

• Retrieve: Given a target problem, relevant

stored cases are retrieved. A case consists of a

problem, its solution, and, typically, annotations

about how the solution was derived.

• Re-use: Map the solution from the previous case

to the target problem. This may involve

adapting the solution as needed to fit the new

situation.

• Revise: Having mapped the previous solution to

the target situation, test the new solution in the

real world (or a simulation) and, if necessary,

revise.

• Retain: After the solution has been successfully

adapted to the target problem, store the resulting

experience as a new case in memory.

The CBR process in general and the retrieval phase

in particular are the focus of the matching engine we

describe in this paper. The general design principles

that have guided the development of the matching

engine are presented in the following section, as well

as the case matching pipeline we have constructed.

Section 3 focuses on the internal workings of the

matching process, for which various operators

derived from fuzzy set theory are used. Section 4

investigates the scalability of the fuzzy matching

engine, by varying the case complexity and the

number of cases. We conclude in Section 5 by

presenting relevant enterprise matching applications

and indicating future research opportunities and

challenges.

375

HANSENNE R., VAN POUCKE J., VAN DER SLUYS V. and VAN DE WALLE B. (2004).

DESIGN AND IMPLEMENTATION OF A SCALABLE FUZZY CASE-BASED MATCHING ENGINE.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 375-382

DOI: 10.5220/0002645903750382

 SciTePress

2 DESIGN OF THE MATCHING

ENGINE

While our focus in this paper is on case-based

reasoning problem solving, it must be noted that it

was our overall design goal to develop a generic

framework for reasoning about data, and to allow

extensions of our framework towards other AI

technologies, such as clustering, re-inforcement

learning, neural networks and expert systems (Pal et

al., 2001).

2.1 Design layers overview

2.1.1 Algorithm Layer

This layer is concerned with the actual

implementation of the matching algorithms.

Moreover, Layer 1 controls the scalability of the

engine, e.g. by running certain matching algorithms

in parallel. To the end user, the Algorithm Layer is

the most abstract layer: there is no graphical user

interface (GUI) to directly interact with this layer.

The functionality of this layer is, in short, restricted

to matching one data set to another. This layer does

not ‘know’ where the data sets come from, or where

they will be further processed. This is taken care of

by the second layer, the Management Layer.

2.1.2 Management Layer

The Management Layer is an intermediate layer

between the Algorithm Layer and the Application

Layer and makes abstraction of the communication

between these two layers. This layer provides

management functionality to the matching engine,

for example security, data import from files, data

bases or data stores, user management, etc. This

layer must enable those users who have no specific

technical knowledge about the matching algorithms

or the structure of the datasets to work with the

matching engine.

2.1.3 Application Layer

The Application Layer, is the front end of the

software engine application. Layer 3 contains the

software which actually makes use of the matching

engine, and can add its own functionality to the

application. Dedicated GUIs can be developed and

other applications can be integrated within this layer.

Other applications such as search engines, web

services or autonomous agents can make use of the

data that have been matched.

2.2 The matching engine pipeline

The flow of the fuzzy matching engine as shown in

Figure 2 below can in essence be viewed as a

traditional input - output process, where the input

consists of one or more cases (the actual query), the

process is the fuzzy matching process, and the

output consists of the cases that have been matched

(the actions). This process is iterative: the output of

the process can be fed back into the engine, and re-

used for a subsequent or new matching query.

The different steps in the ‘pipeline’ of Figure 2 are

elaborated below. In principle, every step should be

individually configurable (at startup time and run

time), and controlled by a “step manager”. We are

currently exploring the development of a separate

workflow engine which controls each step of the

process and also indicates which loop-backs should

be performed.

2.2.1 Cases

Cases are the start of the process and are typically

created in Layer 2, the Management Layer. A case is

defined as a set of different properties, with every

property describing a single attribute on which a

matching is requested. Any property can have one of

the following formats: Boolean, Ordinal

(qualitative), Numeric (quantitative), Alpha numeric,

Fuzzy (vague) or Unknown. These properties are

extensible, as we do not know beforehand which

other data types may be needed. We only know that

they are atomic and that they form the basis upon

which will be matched. Properties also have meta-

information. They can have a weight to describe the

importance of an individual property, a ranking

relative to other properties and a veto power on other

properties that are not compatible. Some properties

can be converted into another format. For example, a

Numeric property is a special case of a Fuzzy

property, and hence could be converted into a Fuzzy

one without loss of precision or information. Cases

are stored in memory, which can be persistent or

transient.

Figure 1: The matching engine pipeline

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

376

2.2.2 Pre-processing

The pre-processing step occurs before the actual

matching. While this step is not part of the actual

matching algorithm, it is, globally speaking, part of

the matching process. This step is not intended to

create cases or do property extraction from some

source, but rather to do some manipulation on the

properties of a case. The pre-processing is a queue

of zero, one or more pre-processing steps, but each

step is independent of the other. As such, they run

sequentially in a well defined order. The pre-

processing is not required; actually, a valid

implementation is one that simply let pass all cases

without modifying them.

2.2.3 Matching

The matching step is the heart of the workflow. Here

we select the algorithm to match cases against

others. The actual implementation can differ, and

one could choose for a simple sorting of cases or

instead perform complex clustering algorithms. For

our purposes, there are some requirements upon the

matching step. We must be able to handle unknown

and incomplete data, or more specifically, we must

be able to handle cases where some or more

properties are absent, unknown or invalid. As a

result of the matching step, we obtain a result or

conclusion. This result can be partially complete, but

it always has received a score which indicates how

well the case matches with other cases.

2.2.4 Post-processing

The post-processing step acts on the result of the

matching step and is optional, as was the pre-

processing step. In this step, for instance, we could

decide to store intermediate results.

2.2.5 Selection of actions and matching

loops

In principle, the workflow process could run in an

endless loop: the result of the matching step can be

fed again into the initial ‘cases’ step. However, an

action is associated with the conclusion of every

single loop. This allows us to act upon partial results

that have been obtained during the matching or

reasoning. The main reason for having a loop is to

make the matching process more powerful. The

algorithm of the matching can be selected before we

perform the loop. In a first loop, we could match the

cases with one particular algorithm and perform a

second loop with another algorithm. This can be

repeated until we are satisfied with the result or with

a pre-defined number of times. The result is a

matching flow which consists of several smaller

matching loops, running in parallel or sequential.

3 FUZZY MATCHING PROCESS

3.1 Introduction

The fuzzy case-based matching engine is capable of

comparing the properties of a set of cases and

produces a matching result indicating the degree to

which every two cases match. As mentioned earlier,

a case is any uniquely identifiable entity (a product

description, a buyer preference, a CV,…) containing

property values for certain criteria. For example,

criteria may be “color” and “price” and their

corresponding property values might be “red” and

“100$”, respectively.

In the remainder of this section, we describe the

internal workings of the engine in more detail.

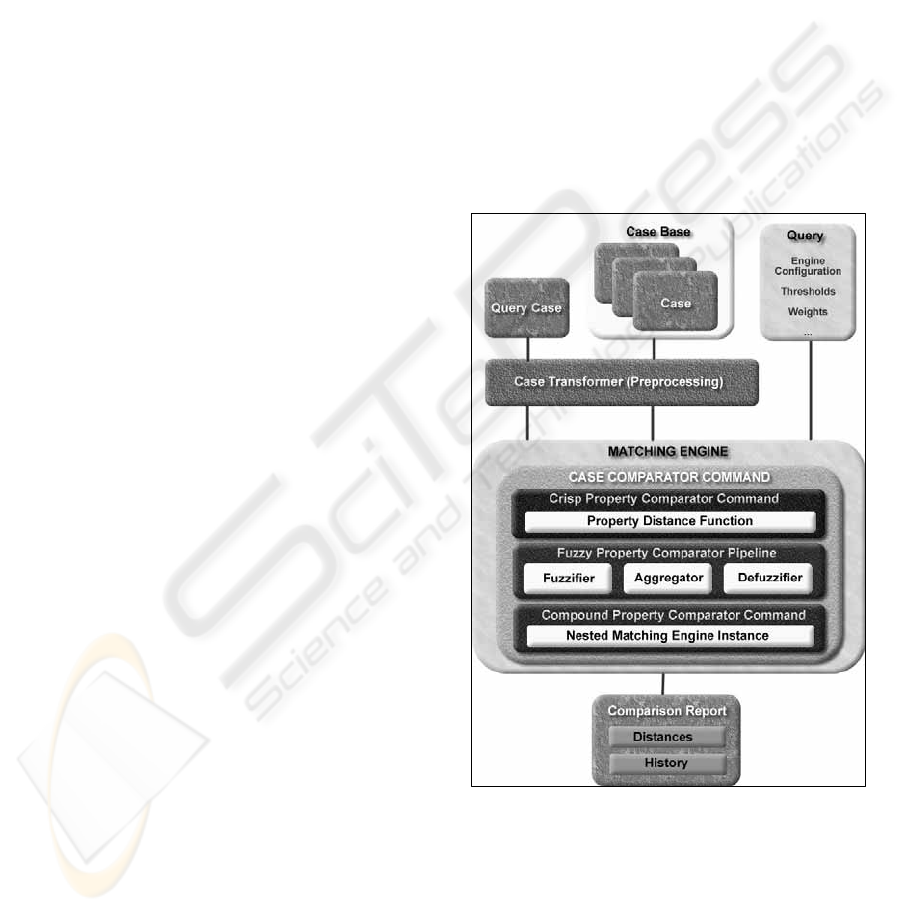
Figure 2: The fuzzy matching engine’s internal

functionality

DESIGN AND IMPLEMENTATION OF A SCALABLE FUZZY CASE-BASED MATCHING ENGINE

377

3.2 Input and internal data type

representation

Internally, the fuzzy engine performs its operations

using fuzzy data types. The property values of the

input cases may be defined in both a crisp (e.g. a

number or a range) or fuzzy (based on a membership

function) data type. Table 1 summarizes the

different data types that can be used in the fuzzy

engine.

Table 1: Matching engine data types

Numerical A (crisp) number which can be

represented with double

precision

Discrete set A finite list of options. An option

can be any uniquely identifiable

object. An example of a discrete

set would be {“red”, “blue”,

“orange”}.

Weighted

Discrete Set

Identical to a standard discrete

set, however every set member

has an associated weight or

membership value (in the

interval [0,1]). This allows an

application to use fuzzy

modifiers for each et member,

each mapping to a certain

weight. For instance: 25%=“a

little”;50%=”somewhat”;

75%=”quite”,…

Range A single continuous numerical

range.

Range Set A unique set of ranges

Weighted

Range Set

A range set, with weights

associated to every range. This is

a generalization of a weighted

discrete set.

Fuzzy Set A fuzzy value, represented by a

function.

Case Properties may be compound.

For example a property “price”

may be a composition (linear

function) of “base price”, “VAT”

and “s&h”. These compound

properties are modeled as sub-

cases containing properties for

the sub-criteria.

Before comparing property values, the engine

converts any non-fuzzy property value into a fuzzy

value at the pre-processing phase. The matching

engine works with both point-functions and piece-

wise linear functions as membership functions for

fuzzy values. These can represent all the most

frequently used fuzzy set membership functions

(triangular, trapezoid…) and allow an approximation

of others, such as Gauss curves (De Baets et al.,

1989; Klir and Bo, 1995).

In order to match the properties of two distinct

cases, three standard operations need to be

performed: the fuzzification of the property values,

the aggregation of these fuzzy values, and the

defuzzification of the aggregation into a crisp

matching value, respectively (Xu et al., 2001). We

discuss each of these steps in the following sections

in some more detail.

3.3 Fuzzification

In order to convert crisp input values into fuzzy

values, a method of fuzzification needs to be

selected. A wide variety of fuzzification methods

exists, and the most suitable method for the case at

hand will depend on the usage context. Three

standard methods have been implemented in the

engine. In addition, specific fuzzification operations

can be performed in higher level applications,

simply by creating the appropriate function and

passing the result as a fuzzy property value to the

engine. The following fuzzification methods have

been implemented.

• Range-based fuzzification: This method

fuzzifies the value over a domain (UoD or

Universe of Discourse). The fuzzification factor

(a number in the interval [0,1]) indicates over

which percentage of the domain the value will

be fuzzified. The UoD width indicates how

wide the function domain is. The greater the

range, the wider the resulting fuzzy function

will be. In other words, this method assumes

that properties with a broader value domain

(e.g. “price” in interval [0-10.000]) need not be

matched as precise as properties with a narrow

domain (e.g. “age” in interval [25-65]). An

example: a numerical value is 1000 and the

domain is 0-2000. A triangular fuzzification

with fuzzification factor 0.1 will result in a

function with base x-coordinates 900-1100. The

same fuzzification over a domain 900-1100 will

result in a function with base 990-1010. This

ensures that the fuzzification is meaningful in

the specific UoD context.

• Fixed fuzzification: If no domain is available

however, the method for fixed fuzzification or

value-oriented fuzzification (presented next) can

be applied. The fixed fuzzification results in a

function with a specified base width, which

does not depend on the actual value. An

example: a numerical value is 1000 and the

fuzzification is 250. The resulting function will

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

378

have a base with x-coordinates 875-1125.

Clearly, this method of fuzzification should

only be used when no UoD is known, as the

fuzzification would be meaningless if the

domain is extremely wide (for example 0-

1.000.000) and exaggerated if the domain is

very narrow (for example 900-1100).

• Value-based fuzzification: This fuzzification

results in a function with a base width,

depending in the actual value. The greater the

value, the wider the base. An example: the value

is 100 and the fuzzification is 0.1. The resulting

function will have a base with x-coordinates 90-

110 (width=20). The same fuzzification on a

value of 1000 will result in a base 900-1100

(width=200). This fuzzification method is

therefore only applicable in certain contexts,

where larger values require less precise

matches.

Besides the fuzzification method, a fuzzifying

function needs to be defined. Depending on the

application context, this might for instance be a

triangular, trapezoid or Gauss function.

3.4 Aggregation

The second step is to aggregate the fuzzified values

in order to determine the degree to which these

values correspond. Three standard methods have

been implemented in the engine and, as was the case

for the fuzzification operations, additional

aggregation methods such as product or union can

be easily implemented by higher level applications.

The implemented methods are the following.

• Intersection: The intersection operator models

the fuzzy ‘AND’, and aggregates two fuzzy sets

using function intersection. Intersection is a

very strict yet commonly used form of

aggregation. Using fuzzy intersection, two

properties will only match well if they both

contain high membership values.

• Absolute difference: The absolute difference

aggregates two fuzzy sets into a function

representing the absolute difference of both.

The absolute difference between piecewise

linear functions is a new piecewise linear

function, and the absolute difference between a

point and a piecewise linear function is a new

point function. The difference aggregation does

not take into account the actual values of the

points, but only compares the amount in which

the both values differ. As a result, two very low

values might match much better than a low and

a high value. In certain contexts this might not

be the expected behavior and in these cases a

different aggregator should be used.

• Bounded difference: The bounded difference

determines the fuzzy difference between two

functions f

and f

, with a lower bound of 0. In

other words, the difference is max(f

-f

,0). In

contrast to the other aggregators, the order of

the functions is important here. Indeed, the

bounded difference of f

and f

is not

necessarily equal to the bounded difference of f

and f

. As with the absolute distance, this

aggregator is not suited for every form of

matching as a set of low preferences might

result in a perfect or near-perfect matching

score.

3.5 Defuzzification

The aggregation step is followed by a final step of

defuzzification a distance or matching value. This

resulting value is a measure for the similarity of two

property values. Depending on the data type of one

or both of the properties, either a numerical value or

range (partial matching) will be returned. As before,

additional operators can be easily added at the

Application layer, but the following operators are

available by default.

• Max: Simply returns the maximum membership

value of a fuzzy value. This can be used to

determine the maximum intersection value of

two properties and will be used most often in

fuzzy matching. However, if at least one of the

properties is a discrete set and the property

should only receive a high score if all of the

options in the set match well, average

intersection or a matching based on difference-

aggregation should be used. The max

defuzzification used in combination with a

bounded or absolute difference aggregation only

compares the similarity of property values,

without taking into account the actual values

themselves. This means, two properties with

both low, nearly equal values will score match

very closely. In some cases, this is not expected

behavior. In those cases distance function based

on intersection can be used.

• Average: Returns the average function value.

This property distance can be used when at least

one of the properties is a discrete set and the

property should only receive a high score if all

of the options in the set match well. If the

property score should reflect the score of the

best matching option, Max-Intersection should

be used instead.

DESIGN AND IMPLEMENTATION OF A SCALABLE FUZZY CASE-BASED MATCHING ENGINE

379

100

120

140

160

180

200

1 10 100 1000

Crisp matching 1st run

Crisp matching 2nd run

Fuzzy matching 1st run

Fuzzy matching 2nd run

100

150

200

250

300

350

400

110100

Crisp matching 1st run

Crisp matching 2nd run

Fuzzy matching 1st run

Fuzzy matching 2nd run

.))0),()(max(1(

∑

−− xSxU

|))()(|1(

2,1

∑

∑∑

−−

iii

xSxU

3.6 Matching

Once all property distances are computed for each of

the matching criteria, these distances can be turned

into a case distance. Several case distance functions

are available, however the weighted sum will be

used most frequently in fuzzy matching (Zadeh

1971).

Combining an intersection aggregator and a Max

defuzzification, will result in a matching value

defined as

with Ui and Si property values for a criterion Ci and

Wi a weight for the criterion Ci. Combining an

absolute difference aggregator and an Avg

defuzzification, will result in

The bounded difference and Avg defuzzification

amount to (unweighted):

4 FUZZY MATCHING ENGINE

SCALABILITY TESTING

This section provides a brief overview of the

performance of the fuzzy case-based matching

engine.

The benchmarks were performed under the

following test conditions: Hardware: P4-2,66Ghz,

512Mb Ram; Software: Windows XP, JDK1.4.1

Configuration: Single threaded; Fuzzy config: Fixed

value fuzzification (other fuzzification types are

marginally slower). All times are represented in

milliseconds (ms). Two runs are performed per

evaluation, to ensure initialization and configuration

of the matching engine are not taken into account.

4.1 Case scaling

This test benchmarks matching speed for cases with

a single property, in order to evaluate the scaling in

function of the amount of cases. 1000 cases are

evaluated in approximately 140 ms when fuzzy logic

is used.

Using a plain CBR algorithm, 1000 cases are

evaluated in approximately 110 ms. The chart also

illustrates that the engine scales in a logarithmic and

not a linear fashion. This means the engine works

optimally when processing a large amount of cases.

4.2 Property scaling

This test benchmarks matching speed for a single

case, with an increasing amount of properties.

Here we note that the fuzzy algorithm

implementation is faster than standard CBR when

)))(),(((

2,1

∑

iii

xSxUMinMaxW

Figure 3: Results of the case scaling tests for the fuzzy

matching engine

Figure 4: Results of the property scaling test for the

fuzzy matching engine

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

380

100

200

300

400

500

600

700

10 100 1000

Crisp matching 1st run

Crisp matching 2nd run

Fuzzy matching 1st run

Fuzzy matching 2nd run

100

200

300

400

500

600

700

800

900

10 100 1000

Fuzzy matching 1st run

Fuzzy matching 2nd run

processing a limit amount of cases with a large

amount of properties.

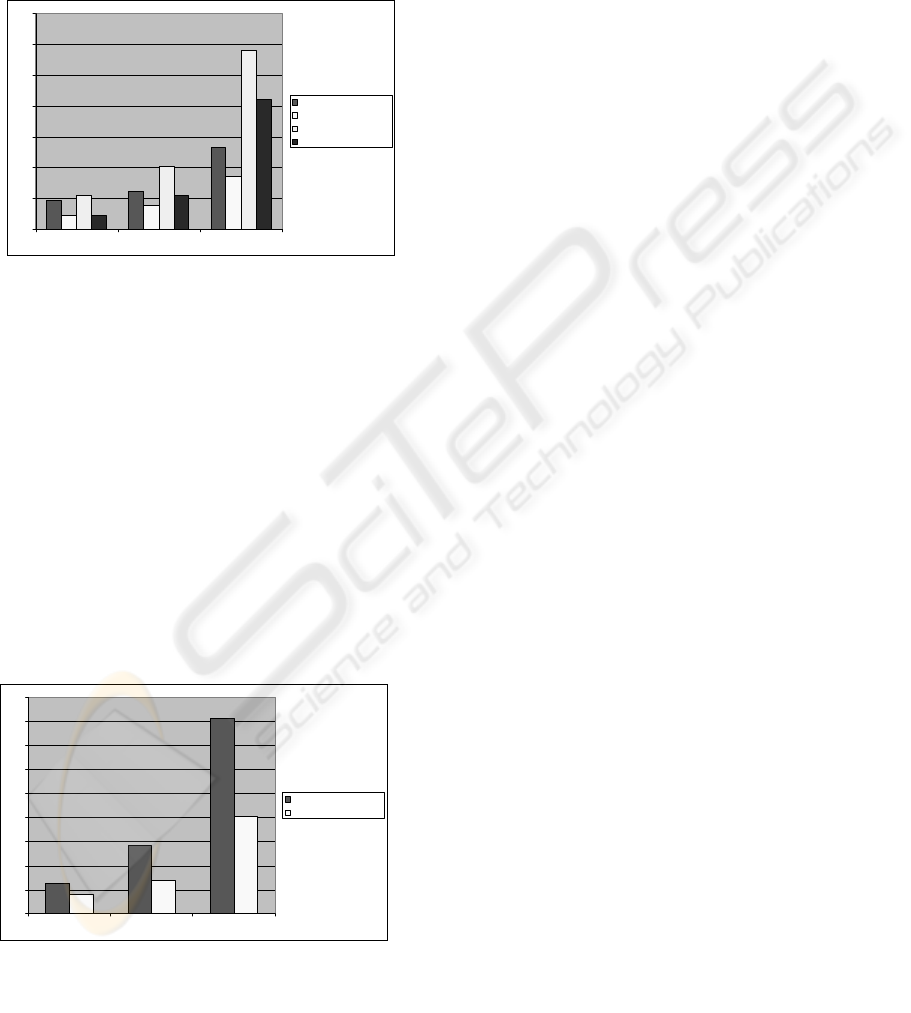
4.3 Real-world scaling

This benchmark tests matching speed for an

increasing amount of cases, with 10 properties each.

Most cases in real world applications can be

represented with no more than 10 properties, so that

this test gives a good idea of real world

performance. 1000 cases can be ‘fuzzy’ matched

against each other in approx. 400 ms (180 ms for

standard CBR). This means the matching engine is

capable of performing 25,000 fuzzy matches per

second, which is faster than most databases can

produce the data required for the matching.

4.4 Fuzzy scaling

All previous benchmarks were performed on pure

numerical properties. This benchmark tests the fuzzy

matching speed for an increasing amount of cases.

Each case contains 7 properties, of which 2 are

compound and nested within each other. Properties

are created randomly and are of types numeric,

interval, discrete weighted set, range set and fuzzy.

Matching 1000 cases takes approximately 400 ms.

5 CONCLUSIONS AND FUTURE

WORK

We have presented design and implementation

issues that have influenced and defined the

development of a fuzzy case-based matching engine.

We stressed the flexibility of the engine, which is

reflected in the variety of case data types on the one

hand and fuzzy set theoretical matching operations

on the other hand. We have analyzed the scalability

of the engine, and found that the engine is capable of

dealing with complex cases under increasing load

conditions. The applicability of the matching engine

is currently being investigated for e-marketplaces for

student jobs (Kurbel et al., 2001; Hansenne et al.,

2003; Van de Walle 2003(b); Hansenne et al., 2004)

and negotiation processes in electronic markets

involving complex multi-issue cases (Van de Walle

et al., 2001). We have recently developed a

theoretical model to deal with incomplete case

information and asymmetric matching processes

(Van de Walle and Van der Sluys, 2002; Van de

Walle 2003(a)), and our near term research objective

is to implement that model in the engine’s

application layer and investigate its applicability for

real world electronic markets.

REFERENCES

Aamodt, A. and E. Plaza, 1994. Case-Based Reasoning:

Foundational Issues, Methodological Variations, and

System Approaches. In AICom - Artificial Intelligence

Communications, IOS Press 7 (1), 39 – 59.

De Baets, B., M.M. Gupta and E.E. Kerre, 1989. Expert

knowledge representation by means of piecewise linear

fuzzy quantities. In Proceedings of the Third

International Fuzzy Systems Association Congress 89

(Seattle, WA, USA), 618-621.

Hansenne, R., V. Van der Sluys and B. Van de Walle,

2003. Smart Web Services in Action: Student Odd

Jobs on University Websites. In Proceedings of the

International Conference on Information Technology:

Research and Education ITRE2003 (Newark, New

Jersey USA), 255 – 256.

Hansenne, R., V. Van der Sluys and B. Van de Walle,

2004. Implementation of a web services based

recruitment platform. Submitted to WSMAI-2004, The

International Workshop on Web Services –

Figure 5: Results of the real-world scaling tests for

the fuzzy matching engine

Figure 6: Results of the fuzzy scaling tests for the

fuzzy matching engine

DESIGN AND IMPLEMENTATION OF A SCALABLE FUZZY CASE-BASED MATCHING ENGINE

381

Modeling, Architecture and Infrastructure (Porto,

Portugal).

Klir, G. and Y. Bo, 1995. Fuzzy Sets and Fuzzy Logic:

theory and Applications. Prentice Hall, Englewood

Cliffs, NJ.

Kolodner, J., 1993. Case Based Reasoning. Morgan

Kaufmann Press.

Kurbel, K.; Loutchko I.; Klaue S.: Automated Negotiation

on Agent-Based E-Marketplaces: An Overview; in:

O'Keefe, B. et al. (Eds.): Proceedings of 14th Bled

Electronic Commerce Conference; Bled, Slovenia;

June 2001, pp. 508-519.

Pal, S., T. Dillon, and D. Yeung, (Eds.), 2001. Soft

Computing in Case Based Reasoning. London, U.K.:

Springer-Verlag.

Van de Walle, B., S. Heitsch and P. Faratin, 2001. Coping

with One-to-many Multi-criteria Negotiations in an

Electronic Marketplace. In Proceedings of the e-

negotiatons Workshop at the 17

International

Database and Expert Systems Applications Conference

DEXIA’01 (Munchen, Germany), 747 –751.

Van de Walle, B. and V. Van der Sluys, 2002. Non-

symmetric Matching Information for Negotiation

Support in Electronic Markets. In Proceeding of the

International Workshop on Information Systems

EuroFuse2002 (Trento, Italy), 271 – 276.

Van de Walle, B., 2003(a). A relational analysis of

decision makers’ preferences. In International Journal

of Intelligent Systems 18, 775 – 791.

Van de Walle, B., 2003(b). Relational structures for the

analysis of decision information in electronic markets.

In Applied Decision Support with Soft Computing

(Eds. X. Yu and J. Kacprzyck), Studies in Fuzziness

and Soft Computing Series Vol. 124, Springer-Verlag,

pp. 196 – 217.

Watson, I.D., 1997. Applying Case-Based Reasoning:

Techniques for Enterprise Systems. Morgan Kaufman

Publishers.

Xu, Y., E.E. Kerre, D. Ruan and Z. Song, 2001. Fuzzy

reasoning based on the extension principle. In

International Journal of Intelligent Systems 16, 469 –

495.

Zadeh, L.A., 1971. Similarity relation and fuzzy orderings.

In Information Sciences 3, 177 – 200.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

382