
A Pitfall in Determining the
Optimal Feature Subset Size
Juha Reunanen
ABB, Web Imaging Systems
P.O. Box 94, 00381 Helsinki, Finland
Abstract. Feature selection researchers often encounter a p eaking phe-
nomenon: a feature subset can be found that is smaller but still enables
building a more accurate classifier than the full set of all the candidate
features. However, the present study shows that this peak may often be
just an artifact due to the still too common mistake in pattern recogni-
tion — that of not using an independent test set.
Keywords: Peaking phenomenon, feature selection, overfitting, accuracy
estimation
1 Introduction
Given a classification (or regression) problem and a potentially large set of can-
didate features, the feature selection problem is about finding useful subsets
of these features. Doing this selection automatically has been a research topic
already for decades.
Why select only a subset of the features available for training an automatic
classifier? Many reasons can be found, such as the following [see e.g. 1, 2, 3]:
1. The accuracy of the classifier may increase.
2. The cost of acquiring the feature values is reduced.
3. The resulting classifier is simpler and faster.
4. Domain knowledge is obtained through the identification of the salient fea-
tures.
Of these reasons, this pap er discusses the first one. Finding a feature subset
that increases the accuracy of the classifier to be built can indeed be seen as an
important motivation for many feature selection studies [2, 4, 5, 6, 7].
The assumption that removing the bad features increases the accuracy derives
from the well-known difficulty of coping with an increasing number of features,
which is often referred to as the curse of dimensionality [8, p. 94]. This difficulty
suggests the peaking phenomenon: the peak of the classification accuracy lies
somewhere between using no features and using all the available features.
If the full probability distributions of the features with respect to the different
classes were known, then one could in theory derive an optimal classification
b ehavior called the Bayes rule, which would exhibit no peaking at all [see e.g.
Reunanen J. (2004).
A Pitfall in Determining the Optimal Feature Subset Size.
In Proceedings of the 4th International Workshop on Pattern Recognition in Information Systems, pages 176-185
DOI: 10.5220/0002650001760185
Copyright
c
SciTePress

9]. However, it can be shown that with just a small amount of ignorance, this
no more holds and additional features may start to have a detrimental effect on
this rule: peaking starts to occur. For instance, this may happen as soon as you
have to estimate the means of the distributions from a finite dataset, even if you
know that the distributions are Gaussian with known covariance matrices [10].
Many empirical studies find this theoretically plausible peak in the accuracy,
but it is unfortunately not always shown using an independent test set that the
smaller, seemingly better (even “optimal”) feature subset that is found actually
gives better results than the full set when classifying new, previously unseen
samples. This paper points out how the failure to perform such a test may result
in almost completely invalid conclusions regarding the practical goal of having
a more accurate classifier.
2 Methodology
The results presented in this paper consist of a number of experiments made
using different kinds of datasets and different kinds of classification methods,
with two different feature selection algorithms. Common to the experiments
however is the use of cross-validation estimates to guide the feature set search
process.
2.1 Feature Selection
Sequential Forward Selection (SFS) is a search method used already by Whitney
[11]. SFS begins the search with an empty feature set. During one step, the
algorithm tries to add each of the remaining features to the set. The benefits
of each set thus instantiated are evaluated and the best one is chosen to be
continued with. This process is carried on until all the features are included, or
a prespecified number of features or level of estimated accuracy is obtained.
On the other hand, Sequential Forward Floating Selection (SFFS) [4] is sim-
ilar to SFS, but employs an extra step: after the inclusion of a new feature, one
tries to exclude each of the currently included features. This backtracking goes
on for as long as better subsets of the corresponding sizes than those found so
far can be obtained. However, extra checks as pointed out by Somol et al. [12]
should take place in order to make sure that the solution does not degrade when
the algorithm after some backtracking goes back to the forward selection phase.
To perform the search for good feature subsets, SFS and SFFS both need a
way to assess the benefits of the different feature subsets. In order to facilitate
this, cross-validation (CV) is used in this paper. In CV, the data available is
first split into N folds with equal numbers of samples.
1
Then, one at a time
each of these folds is designated as the test set, and a classifier is built using
the other N − 1 sets. Then, the classifier is used to classify the test set, and
1
In the experiments of this paper, the classwise distributions present in the original
data are preserved in each of the N folds. This is called stratification.
177

when the results are accumulated for all the N test sets, an often useful estimate
of classification performance is obtained. The special case where N is equal to
the number of samples available is usually referred to as leave-one-out cross-
validation (LOOCV).
2.2 Classification
To rule out the possibility that a particular choice of the classifier metho dology
dictates the results, three different kinds of classifiers are used in the experiments:
1. The k nearest neighbors (kNN) classification rule [see e.g. 9], which is rather
p opular in feature selection literature. Throughout this paper, the value of
k is set to 1.
2. The C4.5 decision tree generation algorithm [13]. The pruning of the tree as
a post-processing step is enabled in all the experiments.
3. Feedforward neural networks using the multilayer perceptron (MLP) archi-
tecture [see e.g. 14], trained with the resilient backpropagation algorithm
[15]. In all the experiments, there is only one hidden layer in the network,
the number of hidden neurons is set to 50, and the network is trained for
100 epochs.
Unlike the kNN rule, the C4.5 algorithm contains an internal feature selection
as a natural part of the algorithm, and also the backpropagation training weighs
the features according to their observed benefits with respect to the cost function.
Such approaches for classifier training are said to contain an embedded feature
selection mechanism [see e.g. 1]. However, this does not prevent one from trying
to outperform these internal capabilities with an external wrapper-based search
[16] – indeed, results suggesting that an improvement is possible can be found
for both the C4.5 algorithm [5, 17] and feedforward neural networks [18].
3 Experiments
The datasets used in the experiments are summarized in Table 1. Each of them
is publicly available at the UCI Machine Learning Repository.
2
Before running the search algorithms, each dataset is divided into the set
used during the search, and an independent test set. This division is regulated
through the use of the parameter f (see Table 1): the dataset is first divided into
f sets, of which one is chosen as the set used for the search while the other f − 1
sets constitute the test set. Note that this is not related to cross-validation, but
the purpose of the parameter is just to make sure that the training sets do not
get prohibitively large in those cases where the dataset has lots of samples. CV
is then done during the search in order to be able to guide the selection towards
the useful feature subsets.
2
http://www.ics.uci.edu/∼mlearn/MLRepository.html
178

Table 1. The datasets used in the experiments. The number of features in the set is
denoted by D. One out of f sampled sets is assigned as the set used during the search
(see text). The classwise distribution of the samples in the original set is shown in the
next column, and the number of training samples used (roughly the total number of
samples divided by the value in column f) is given in the last column, denoted by m.
dataset D f samples m
dermatology 33 2 20–112 (total 366) 184
ionosphere 34 2 126 and 225 176
optdigits.tra 64 5 376–389 (total 3823) 764
sonar 60 2 97 and 111 105
spambase 57 5 1813 and 2788 921
spectf 44 2 95 and 254 175
tic-tac-toe 9 2 332 and 626 479
waveform 40 5 1653–1692 (total 5000) 1000
wdbc 29 2 212 and 357 284
wpbc 32 2 47 and 151 99
3.1 Incorrect Method
How does one evaluate the benefits, i.e. the increase in classification accuracy,
due to performing feature selection? This can be done by comparing the best
feature subset found by the search process to the full set containing all the
candidate features. A straightforward way to do this is to compare the accuracy
estimates that are readily available, namely those determined and used by the
feature selection method during the search, to decide which features to include.
In this study, these numbers are the cross-validation estimates.
If this is done for example for one sampled fifth of the waveform data using
a 1NN classifier, SFS and LOOCV, the solid line in Fig. 1 can be obtained. It
appears that the optimal number of features is 12. Moreover, the peaking phe-
nomenon seems evident, suggesting that feature selection is useful in fighting the
curse of dimensionality because several unnecessary and even harmful features
can be excluded. By choosing the suggested feature subset of size 12 instead of
the full set of all the 40 features, one can increase the estimated classification
accuracy from about 74% to over 79%.
What is wrong here is that the accuracy estimates that are used to plot the
solid line are the same estimates as those that were used to guide the search
algorithm to the most beneficial parts of the feature subset space. Thus, these
estimates are prone to overfitting, and the effect of this fact will be shown in the
following.
3.2 Correct Method
If no extra data is available for independent testing, the best set found in the
previous section, that with the highest cross-validation estimate and, in case of
a draw, the smallest number of features, seems to be the most obvious guess
179

for the best feature subset. In the following, this subset is referred to as the
apparently best subset. In Fig. 1, the apparently best subset would be the one
found by the search process that has exactly 12 features.
If a proper comparison is to be made, the potentially overfitted results found
by the search algorithm during the search should not be used to compare the
apparently best subset and the full set. Instead, independent test data not shown
during the search has to be used. When 1NN classifiers are constructed using
the feature subsets found, and the remaining four fifths of the waveform data are
then classified, the dashed line in Fig. 1 is obtained. It is now easy to see that
the peaking phenomenon applies only to the LOOCV estimates found during
the search, not to the accuracy obtained with the independent test data. In
fact, when comparing the apparently best subset to the full set, instead of the
increase of more than five percentage points mentioned in Sect. 3.1, a decrease
of 2.4 points is observed here.
The apparently best feature subset may seem to be very useful compared to
the full set when the evaluation scores found during the search are used in making
the comparison, but the situation can change remarkably when independent test
data is used. Why this discrepancy takes place can be easily understoo d by
recalling that there is only one candidate for the full feature set with D features,
but
D
d
candidates for subsets of size d. If, for example, D = 40 and d = 20, it
5 10 15 20 25 30 35 40
60
62
64
66
68
70
72
74
76
78
80
Number of features
Estimated classification accuracy (%)
LOOCV
independent test
Fig. 1. 1NN classification accuracies for the feature subsets of the waveform dataset
found by SFS, as estimated with LOOCV during the search (solid line) and calculated
for independent test data not seen during the search (dashed line).
180
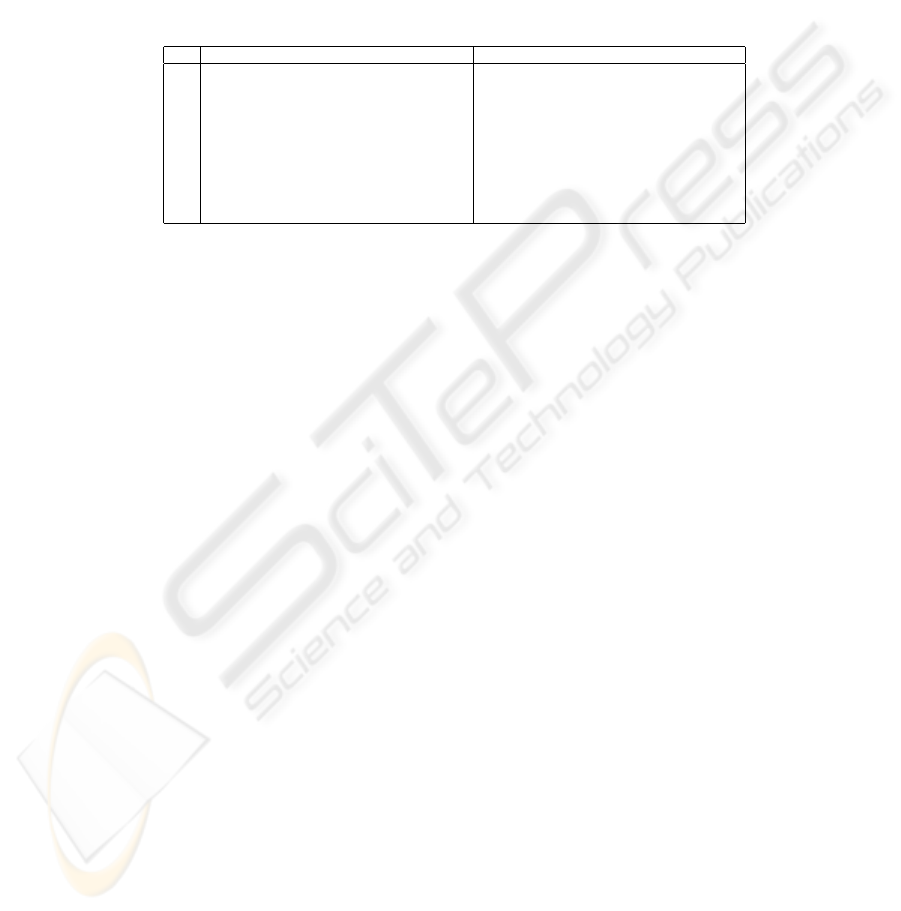
Table 2. The results for the waveform dataset with SFS. The first column indicates
the fraction of the set used during the search that is actually used. The second and the
sixth columns denote the classification and the CV method (LOO is LOOCV, 5CV is
fivefold CV). The third and the seventh columns (d/D) show in percentage the average
size of the apparently best subset as compared to the full set. Further, the fourth and
the eighth columns (∆
CV
) display the increase in estimated classification accuracy due
to choosing the apparently best subset instead of the full set, as measured by the CV
estimate. Finally, the fifth and the ninth columns (∆
t
) show the actual increase as
measured by classifying the held out test data. One standard deviation based on the
ten different runs is shown for each value.
size method d/D (%) ∆
CV
(%) ∆
t
(%) method d/D (%) ∆
CV
(%) ∆
t
(%)
1/16 1NN/LOO 38 ± 11 22 ± 5 −3 ± 4 C4.5/5CV 29 ± 19 19 ± 7 −3 ± 5
1/8 51 ± 16 15 ± 5 −3 ± 2 23 ± 16 16 ± 4 2 ± 2
1/4 52 ± 16 12 ± 4 −0 ± 2 33 ± 11 10 ± 2 −0 ± 3
1/2 58 ± 13 8 ± 3 1 ± 1 44 ± 20 6 ± 2 0 ± 1
1/1 49 ± 17 5 ± 1 1 ± 2 30 ± 11 5 ± 1 0 ± 2
1/16 1NN/5CV 40 ± 1 7 20 ± 7 −2 ± 4 MLP/5CV 23 ± 11 34 ± 5 17 ± 7
1/8 50 ± 16 16 ± 5 −2 ± 3 24 ± 7 31 ± 5 18 ± 5
1/4 51 ± 16 11 ± 3 0 ± 2 22 ± 6 29 ± 4 18 ± 3
1/2 52 ± 10 8 ± 3 1 ± 1 30 ± 9 25 ± 3 19 ± 2
1/1 55 ± 12 5 ± 1 2 ± 0 39 ± 7 16 ± 2 10 ± 2
is not hard to believe that one can find overfitted results amongst the more than
10
11
candidate subsets, those that would be evaluated by an exhaustive search.
This means that the results found during the search process are not only
overfitted, but they are more overfitted for some feature subset sizes than for
some others. This is because the selection of a feature subset for each size is a
model selection process, and there are simply more candidate models the closer
we are to the half of the size of the full feature set. On the other hand, the SFS
algorithm evaluates more candidates for the smaller sizes, which may result in
finding the apparently best subset size to be somewhere between the empty set
and half the full set. However, it seems that if the data is actually so difficult
that the small feature subsets will not do, then the apparently best subset can
also be larger than half the full set.
3.3 More Results
We have seen that the apparently best subset can be superior to the full set when
the comparison is done using the evaluation scores found during the search, but
also that it may turn out that this is not the case when new tests are made with
previously unseen test data. Some further results are now examined in order to
assess the generality of this observation.
Table 2 shows more results for the waveform dataset. Different kinds of classi-
fication methods are used, and all the runs are repeated for ten times — starting
with resampling the set used during the search — in order to obtain estimates for
the variance of the results. Moreover, the effect of the amount of data available
during the search is visible.
The following facts can b e observed based on the table:
181

1. While non-negative by definition, ∆
CV
is always positive and often quite
large. This means that the apparently best subset looks always better and
usually much better than the full set when the CV scores found during the
search are used for the comparison. In other words, the peaking phenomenon
is present, like in the solid curve of Fig. 1.
2. On the other hand, ∆
t
is pretty small — even negative — except for the
MLP classifier. Therefore, the apparently best subset is not much better and
can be even worse than the full set when the comparison is performed using
independent test data. This means that usually there is hardly any peaking
with respect to the size of the feature subset when new samples are classified
— instead, the curve looks more like the dashed one in Fig. 1. Or if there
is a peak, it is not located at the same subset size as the apparently best
subset, and we actually have no means of identifying the peak unless we have
independent test data.
3. Further, ∆
CV
is typically much greater than ∆
t
. This means that there is
lots of overfitting: the apparently best subset appears, when compared to
the full set, to be much better than it is in reality.
4. The difference between ∆
CV
and ∆
t
, i.e. the amount of overfitting, decreases
when the size of the dataset available during the search (column “size” of the
table) increases. This is of course an expected result.
On the other hand, Table 3 shows similar results for all the datasets when
SFS is used. The dependency of the results on the amount of data available
during the search is however largely omitted for the sake of brevity. Still, figures
are shown both for 25% and 100% of the full set.
The four observations made based on Table 2 are valid also for the results in
Table 3. In addition, it is often the case that the size of the apparently best subset
divided by the size of the full set, the ratio d/D, increases when the amount of
data available increases. This is likely b ecause learning the dataset gets more
difficult when the numb er of samples to learn increases, and more features are
needed to create classifiers that appear accurate.
Another interesting fact is that the only case where feature selection clearly
seems to help the 1NN classifier, which does not even have any embedded feature
selection mechanism, is the spambase dataset. However, this is mostly due to
one feature having a much broader range of values than the others. When the
variables are normalized to unit variance as a preprocessing step, the outcome
changes remarkably (record spambase/std in Table 3).
Further, Table 4 shows the results for some of the smaller datasets with the
SFFS algorithm. Represented this way, the results do not seem to differ remark-
ably from those for SFS. However, an examination of figures like Fig. 1 reveals
(not shown) that the subsets found by SFFS are typically more consistently
overfitted, i.e. that there is often a large numb er of subsets that are estimated to
yield a classification accuracy equal or at least close to that obtained with the
apparently best subset, whereas for SFS the apparently best subset is typically
b etter in terms of estimated accuracy than (almost) all the other subsets.
182

Table 3. The results with SFS for all the datasets. For each method there are two
rows. On the first row, the size of the dataset used during the search is one fourth of
the full set, whereas on the second row the full set is used (the size of which is shown in
column m of Table 1). Thus, the first row corresponds to the third and the eighth row
of Table 2, and the second row corresponds to the fifth and the tenth row. Otherwise,
the explanations for the columns equal those for Table 2.
dataset method d/D ∆
CV
∆
t
method d/D ∆
CV
∆
t
dermatology 1NN/LOO 30 ± 17 8 ± 7 −2 ± 4 C4.5/5CV 21 ± 11 5 ± 4 1 ± 3
59 ± 27 2 ± 1 1 ± 1 38 ± 13 2 ± 1 −1 ± 2
1NN/5CV 24 ± 6 5 ± 2 −3 ± 3 MLP/5CV 35 ± 17 20 ± 6 7 ± 4
48 ± 17 3 ± 1 −1 ± 1 54 ± 15 4 ± 2 −0 ± 2
ionosphere 1NN/LOO 18 ± 12 17 ± 6 1 ± 5 C4.5/5CV 40 ± 19 11 ± 4 1 ± 4
21 ± 10 14 ± 2 2 ± 3 30 ± 20 6 ± 2 −0 ± 2
1NN/5CV 20 ± 12 13 ± 5 0 ± 2 MLP/5CV 28 ± 15 14 ± 7 −1 ± 4
27 ± 15 10 ± 2 3 ± 2 24 ± 18 9 ± 3 4 ± 4
optdigits.tra 1NN/LOO 75 ± 17 4 ± 2 −1 ± 1 C4.5/5CV 47 ± 21 9 ± 3 −0 ± 7
72 ± 15 1 ± 0 −1 ± 0 63 ± 16 4 ± 1 −0 ± 2
1NN/5CV 64 ± 13 5 ± 1 −1 ± 1 MLP/5CV 41 ± 10 24 ± 8 16 ± 15
67 ± 12 1 ± 1 −1 ± 0 55 ± 16 8 ± 2 1 ± 3
sonar 1NN/LOO 20 ± 17 27 ± 9 −2 ± 10 C4.5/5CV 22 ± 27 25 ± 13 1 ± 4
55 ± 7 13 ± 4 2 ± 5 30 ± 23 17 ± 4 0 ± 7
1NN/5CV 21 ± 26 32 ± 8 −2 ± 7 MLP/5CV 17 ± 20 23 ± 11 −3 ± 4
35 ± 17 14 ± 3 −2 ± 6 32 ± 13 14 ± 3 −1 ± 4
spambase 1NN/LOO 37 ± 10 26 ± 4 18 ± 2 C4.5/5CV 41 ± 15 6 ± 2 −1 ± 2
49 ± 13 18 ± 2 14 ± 1 54 ± 19 3 ± 1 0 ± 1
1NN/5CV 37 ± 13 26 ± 3 18 ± 1 MLP/5CV 29 ± 12 10 ± 2 1 ± 2
44 ± 15 18 ± 2 14 ± 1 47 ± 12 3 ± 1 0 ± 1
spambase/std 1NN/LOO 37 ± 22 12 ± 3 2 ± 2 C4.5/5CV 34 ± 15 6 ± 2 −0 ± 2
42 ± 10 6 ± 1 3 ± 1 52 ± 20 3 ± 1 0 ± 1
1NN/5CV 30 ± 10 11 ± 4 3 ± 3 MLP/5CV 29 ± 12 9 ± 3 2 ± 2
43 ± 14 5 ± 1 2 ± 2 46 ± 13 3 ± 1 −0 ± 1
spectf 1NN/LOO 21 ± 10 30 ± 11 1 ± 5 C4.5/5CV 20 ± 17 19 ± 6 2 ± 6
37 ± 15 14 ± 3 1 ± 4 39 ± 24 10 ± 3 −2 ± 3
1NN/5CV 20 ± 8 25 ± 6 0 ± 5 MLP/5CV 9 ± 3 18 ± 5 −3 ± 8
34 ± 15 13 ± 4 1 ± 3 9 ± 3 10 ± 2 2 ± 4
tic-tac-toe 1NN/LOO 90 ± 21 1 ± 2 −3 ± 7 C4.5/5CV 69 ± 24 5 ± 3 −1 ± 4
100 ± 0 0 ± 0 0 ± 0 99 ± 4 0 ± 0 −0 ± 0
1NN/5CV 94 ± 6 1 ± 1 −2 ± 3 MLP/5CV 84 ± 15 2 ± 2 −4 ± 4
100 ± 0 0 ± 0 0 ± 0 100 ± 0 0 ± 0 0 ± 0
waveform 1NN/LOO 52 ± 16 12 ± 4 −0 ± 2 C4.5/5CV 33 ± 11 10 ± 2 −0 ± 3
49 ± 17 5 ± 1 1 ± 2 30 ± 11 5 ± 1 0 ± 2
1NN/5CV 51 ± 16 11 ± 3 0 ± 2 MLP/5CV 22 ± 6 29 ± 4 18 ± 3
55 ± 12 5 ± 1 2 ± 0 39 ± 7 16 ± 2 10 ± 2
wdbc 1NN/LOO 12 ± 13 9 ± 5 −2 ± 4 C4.5/5CV 14 ± 8 4 ± 3 0 ± 1
51 ± 34 3 ± 2 0 ± 2 38 ± 18 4 ± 1 1 ± 1
1NN/5CV 17 ± 14 8 ± 5 −0 ± 2 MLP/5CV 22 ± 15 36 ± 1 30 ± 2
34 ± 10 4 ± 1 −1 ± 2 29 ± 12 34 ± 3 33 ± 2
wpbc 1NN/LOO 33 ± 25 29 ± 16 1 ± 5 C4.5/5CV 16 ± 17 23 ± 9 2 ± 4
46 ± 30 15 ± 7 −5 ± 4 31 ± 18 12 ± 4 2 ± 9
1NN/5CV 22 ± 20 23 ± 12 −1 ± 7 MLP/5CV 10 ± 9 11 ± 6 −14 ± 8
31 ± 24 14 ± 4 −4 ± 5 12 ± 12 2 ± 2 −4 ± 5
183

Table 4. Like Table 3, but for SFFS and only a few datasets.
dataset method d/D ∆
CV
∆
t
method d/D ∆
CV
∆
t
dermatology 1NN/LOO 25 ± 11 8 ± 5 −6 ± 3 C4.5/5CV 29 ± 25 10 ± 5 1 ± 2
43 ± 12 3 ± 1 −2 ± 1 44 ± 22 3 ± 1 −0 ± 2
1NN/5CV 35 ± 26 7 ± 4 −4 ± 4 MLP/5CV 39 ± 17 21 ± 4 8 ± 6
56 ± 19 4 ± 1 −1 ± 2 48 ± 12 5 ± 1 1 ± 3
ionosphere 1NN/LOO 17 ± 9 22 ± 10 1 ± 5 C4.5/5CV 34 ± 24 10 ± 6 −2 ± 4
20 ± 6 15 ± 3 1 ± 3 45 ± 18 7 ± 3 1 ± 2
1NN/5CV 23 ± 16 17 ± 7 1 ± 5 MLP/5CV 28 ± 22 13 ± 6 0 ± 5
22 ± 9 11 ± 1 1 ± 3 25 ± 15 9 ± 1 2 ± 3
sonar 1NN/LOO 8 ± 3 31 ± 14 3 ± 4 C4.5/5CV 22 ± 23 29 ± 9 −0 ± 5
24 ± 6 16 ± 3 −1 ± 4 29 ± 20 15 ± 5 1 ± 9
1NN/5CV 23 ± 18 26 ± 11 1 ± 6 MLP/5CV 25 ± 21 23 ± 8 −5 ± 9
40 ± 16 14 ± 4 1 ± 6 33 ± 20 12 ± 3 −3 ± 6
spectf 1NN/LOO 26 ± 13 33 ± 8 4 ± 6 C4.5/5CV 18 ± 15 18 ± 8 2 ± 4
45 ± 14 16 ± 3 2 ± 4 48 ± 23 9 ± 2 −1 ± 4
1NN/5CV 23 ± 12 28 ± 5 3 ± 5 MLP/5CV 9 ± 3 18 ± 4 −2 ± 4
32 ± 15 13 ± 4 0 ± 4 12 ± 3 12 ± 3 2 ± 4
The datasets and the methods used here were chosen rather arbitrarily, which
suggests that some generality of the results can be expected. Still, there are
probably many examples where the results would look completely different —
for instance, there can be datasets that are comprehensive enough that there is
no significant overfitting.
4 Conclusions
The experimental results reported in this paper suggest that the best cross-
validation score found during the search is often obtained with a feature subset
that is much smaller than the full set, and the difference between the scores for
this apparently best feature subset and the full set of all the candidate features
is often significant. Thus, it is possible to come up with a hasty conclusion that
removing some of the features increases the classification score.
However, from the fact that the CV scores found during the search are un-
equally biased for different subset sizes, it follows that the optimal subset size
for independent test data is often not the same as or even close to that of the
apparently best subset. More importantly, the apparently best subset, which
often seems to be superior over the full set when the comparison is based on
the estimates found during the search, may turn out to be even worse when
classifying new data. It appears that in many cases the peaking phenomenon is
not due to the classifier being overwhelmed by the curse of dimensionality (any
more than a feature selection algorithm is), but rather an artifact solely caused
by the overfitting in the search process. Therefore, the results suggest that the
estimates found during the search should not be used when determining the op-
timal number of features to use. Instead, an independent test set — or, if there
is time, an outer loop of cross-validation — is needed.
184

References
[1] I. Guyon and A. Elisseeff. An introduction to variable and feature selection.
J. Mach. Learn. Res., 3:1157–1182, 2003.
[2] M. Kudo and J. Sklansky. Comparison of algorithms that select features
for pattern classifiers. Pattern Recognition, 33(1):25–41, 2000.
[3] M. Egmont-Petersen, W.R.M. Dassen, and J.H.C. Reiber. Sequential se-
lection of discrete features for neural networks — a Bayesian approach to
building a cascade. Patt. Recog. Lett., 20(11–13):1439–1448, 1999.
[4] P. Pudil, J. Novoviˇcov´a, and J. Kittler. Floating search methods in feature
selection. Patt. Recog. Lett., 15(11):1119–1125, 1994.
[5] R. Kohavi and G. John. Wrappers for feature subset selection. Artificial
Intelligence, 97(1–2):273–324, 1997.
[6] D. Charlet and D. Jouvet. Optimizing feature set for speaker verification.
Patt. Recog. Lett., 18(9):873–879, 1997.
[7] P. Somol and P. Pudil. Oscillating search algorithms for feature selection.
In Proc. ICPR’2000, pages 406–409, Barcelona, Spain, 2000.
[8] R. Bellman. Adaptive Control Processes: A Guided Tour. Princeton Uni-
versity Press, 1961.
[9] P.A. Devijver and J. Kittler. Pattern Recognition: A Statistical Approach.
Prentice–Hall International, 1982.
[10] G.V. Trunk. A problem of dimensionality: A simple example. IEEE Trans.
Pattern Anal. Mach. Intell., 1(3):306–307, 1979.
[11] A.W. Whitney. A direct method of nonparametric measurement selection.
IEEE Trans. Computers, 20(9):1100–1103, 1971.
[12] P. Somol, P. Pudil, J. Novoviˇcov´a, and P. Pacl´ık. Adaptive floating search
methods in feature selection. Patt. Recog. Lett., 20(11–13):1157–1163, 1999.
[13] J.R. Quinlan. C4.5: Programs for Machine Learning. Morgan Kaufmann,
1993.
[14] C.M. Bishop. Neural Networks for Pattern Recognition. Oxford University
Press, 1995.
[15] M. Riedmiller and H. Braun. A direct adaptive method for faster backprop-
agation learning: The RPROP algorithm. In Proc. ICNN93, pages 586–591,
San Francisco, CA, USA, 1993.
[16] G.H. John, R. Kohavi, and K. Pfleger. Irrelevant features and the subset
selection problem. In Proc. ICML-94, pages 121–129, New Brunswick, NJ,
USA, 1994.
[17] P. Perner and C. Apt´e. Empirical evaluation of feature subset selection
based on a real world data set. In Proc. PKDD-2000 (LNAI 1910), pages
575–580, Lyon, France, 2000.
[18] A.F. Frangi, M. Egmont-Petersen, W.J. Niessen, J.H.C. Reiber, and M.A.
Viergever. Bone tumor segmentation from MR perfusion images with neural
networks using multi-scale pharmacokinetic features. Image and Vision
Computing, 19(9–10):679–690, 2001.
185
