Intrusion Risk Analysis and the Power Law Distribution

of Attacks

Juan Manuel Garcia Garcia

Department of Computer Systems

Instituto Tecnol´ogico de Morelia

Morelia, Mexico

Abstract. Risk analysis is the ﬁrst essential step in the risk management process.

In order to do an effective risk analysis, is necessary to identify and quantify the

threats to information technology assets. Then statistical models of information

security threats are required to develop effective risk analysis methodologies. We

present experimental evidence suggesting that network intrusion attacks follows

a power law distribution and then we explore some implications for intrusion risk

analysis.

Keywords: Risk analysis, network intrusion detection, power law distribution.

1 Introduction

Risk analysis, also known as risk assessment, is the ﬁrst essential step in the information secu-

rity architecture deployment [11]. Information security controls implemented in any organization

should be commensurate with its risks. The purpose of information security risk analysis is to

determine, on the most objective basis, which security controls are appropriate and cost effective.

There are several approaches to risk analysis. However, these can be classiﬁed into two cate-

gories: quantitative and qualitative. [10]

In the quantitative approach, probability data is not required and only estimated potential

loss is used. The main drawback of this approach is its very subjective nature and that it heavily

relies on the expertise of the risk analysis team’s members. However, it is the most widely used

approach to risk analysis.

The quantitative approach focus on two elements: the probability of an event occurring and

the likely loss should it happen. Quantitative risk analysis make use of a single indicator called

the annual loss expectancy (ALE), calculated for an event as the product of the potential loss by

the probability of the event occurrence. Then it is possible to rank events in order of risk and

to make decisions about control and countermeasures based on this. The effectiveness of this

approach depends on the reliability and accuracy of the statistical data associated with the event.

One of the most important security controls to be considered into an information security

architecture are intrusion detection systems, (IDS) [2][8]. An IDS needs to be cost-effective in

the sense that it should cost no more than the expected level of loss from intrusions. Despite this,

IDS cost-beneﬁt analysis is seldom done.

In a previous work [6], major cost factor associated with an IDS were examined, including

development cost, operational cost, damage cost due to successful intrusions, and the cost of

manual and automated response to intrusions. Cost factors are qualiﬁed according to a deﬁnite

Manuel Garcia Garcia J. (2004).

Intrusion Risk Analysis and the Power Law Distribution of Attacks.

In Proceedings of the 2nd International Workshop on Security in Information Systems, pages 47-52

DOI: 10.5220/0002659500470052

 SciTePress

attack taxonomy [7], which main categories are illegal root access, illegal user access, denial of

service, and information gathering. A cost-beneﬁt analysis methodology for network intrusion

detection had been proposed [12], based on an investigation of the cost factors and categories of

various intrusions.

But, in order to do a full cost-beneﬁt analysis for NIDS, a loss expectancy value must be ob-

tained, and then a model for potential loss and probability of intrusions is required. In this paper,

we present a probabilistic model for network intrusions that follows a power law distribution.

2 Experimental Data on Attacks

In order to get some insight about what kind of probabilistic distribution follows network intru-

sion events we analyse data collected by an IDS over several months. The IDS used was Snort

1.8

using arachNIDS database

of network attacks signatures.

Alert frequency

Rank

1009080706050403020100

2500

2000

1500

1000

500

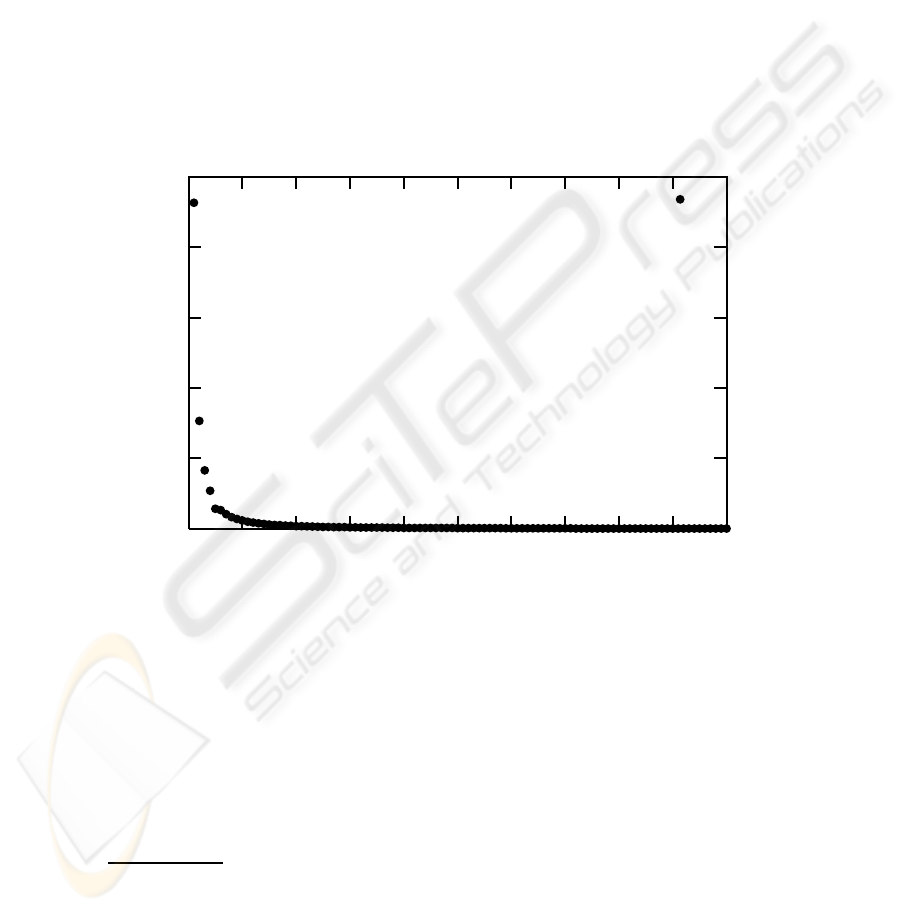
Fig.1. Frequency versus rank of alerts.

Over eight months of observation, 5091 alerts were logged, 137 different kind of attacks

were observed, where arachNIDS database includes more than 500 different attack signatures.

The most frequent kind of attack logged was port scanning, like SYN FIN Scan (IDS198) or

Probe SYN Scan (IDS441), and one of the most rare attacks logged was, for example, a buffer

overﬂow attempt on IMAP service (IDS147) with a single occurrence on the observed period.

Virus and worms attacks were not considered because they are not longer supported by Snort.

After ranking attacks by frequency of occurrence, we observed that the most innocuous at-

tacks, those included in the information gathering category, are also the most frequently seen. We

http://www.snort.org/

http://www.whitehats.com/ids/

observed a high incidence of few probe kind of attack and a very low incidence of more varied

and more dangerous attacks, like buffer overﬂow attempts. In ﬁgure 1 we show a plot of rank ver-

sus frequency, when can be observed how few attacks are most frequently seen. This observation

suggest a power law distribution like that related to many phenomena like Internet trafﬁc [4], web

requests [3], etc.

When we plot rank against frequency in a log-log scale we obtain what is showed in ﬁgure

2. The least-squares regression line is

(1)

where

is the alert frequency, and is the alert rank. Then we have

(2)

Then we can take as cumulative distribution function

(3)

Then we can deduce for intrusion attacks the following probability distribution function

(4)

where

and . The previous PDF is valid only for

. This is the well known power law or Zipf-like distribution [1]. For an unknown

number of attacks, we can generalize the attack distribution to a zeta distribution

(5)

where

is the Riemann’s zeta function evaluated on [5].

3 Implications for Intrusion Risk Analysis

In this section, we explore some implications of the power law distribution of attacks that we

already present, for intrusion risk analysis. Let

be the potential loss caused by the occurrence

of the rank

attack, then the expected loss for a set of attacks would be

(6)

Also we can have a cost

for detection and response to an event of rank , that can be

calculated by the methodology proposed in [6] and [12].

For a ﬁxed budget

, we want to detect and respond to the attacks that could inﬂict the greater

loss. Then we can formulate intrusion risk analysis as a combinatorial optimization problem in

the following way: To ﬁnd a set of possible threats

such that , as deﬁned in (6), is maximized,

subject to the constraint

(7)

In the general case, this problem could be hard to solve, but under some assumptions it could

be simpliﬁed.

First of all, expected loss (6) can be estimated by its continuous limit

(8)

Alert frequency

Rank

6543210

Fig.2. Frequency versus rank of alerts in a log-log scale.

We can observe that this integral can be computed as the Mellin transform [9] of the loss function:

(9)

evaluated at

A simple closed solution can be found under some assumptions. These assumptions are the

following:

1. The potential loss caused by an attack depends only on the kind of attack. That is, the damage

inﬂicted by, for example, a denial of service, is the same doesn’t matter what particular DoS

attack it is. (For this matter, we can use the attack taxonomy presented in [7].)

2. Similar kind of attacks are close ranked. That is, all the attacks of the same category (see

[7]) are ranked in some rank interval

, and all the events ranked in this interval are of

the same kind.

These two conditions are very likely from what we have experimentally observed.

If all attacks of the same kind are ranked in some interval

and the loss caused for any of

them is a constant

then the loss function for that kind of attack can be expressed as the boxcar

function:

(10)

which is equal to

for and otherwise, and where is the Heaviside step function.

The Mellin transform for this function is

(11)

and then, the expected loss for that particular kind of attack would be

(12)

Under assumptions previously stated, attacks can be classiﬁed into different kinds, so that

for all the attacks of kind

, the associated loss to any of them is a constant and all of them

rank between an interval

where is the most probable attack of kind and the least.

Then, we have the expected loss for attack kind

(13)

for

, where the total expected loss would be

(14)

Estimated costs for attack prevention, detection and response are much more easier to obtain

for whole attack kinds than for particular attacks [7]. Thus, if we deﬁne

as the cost associated

to prevention, detection and response to the

attack kind, where , then cost/beneﬁt

analysis can be obtained from

and values using a methodology like the exposed in [12].

4 Conclusions and Future Work

We have presented some experimental evidence suggesting that intruders attacks follows a power

law distribution, very similar to the kind of distribution associated to several aspects of Internet

trafﬁc.

We have shown how this power law distribution can be used to estimate expected losses for

diferent kind of attacks, assuming that the loss inﬂicted by one attack depends only on the kind

of attack and that attacks of the same kind are close-ranked. Further experimental evidence is

needed to verify how valid are these assumptions.

Further experimental study is also required to extend our analysis to virus and worms attacks.

References

1. R. J. Adler, R. E. Feldman and M. S. Taqqu (eds). A Practical Guide to Heavy Tails: Statis-

tical Techniques and Applications, Birkhauser, Boston, 1998.

2. R. G. Bace. Intrusion Detection, QUE, 1st Edition, December 1999.

3. L. Breslau, P. Cao, L. Fan, G. Phillips and S. Shenker. Web caching and Zipf-like distribu-

tions: evidence and implications. Proceedings of INFOCOMM’99, IEEE Press, 2000.

4. A. B. Downey. Evidence for long-tailed distributions in the Internet. ACM SIGCOMM Inter-

net Measurement Workshop, November 2001.

5. H. M. Edwards. Riemann’s Zeta Function. Dover Pubns, June 2001.

6. W. Lee, W. Fan, M. Miller, S.J. Stolfo and E. Zadok. Toward Cost-Sensitive Modeling for

Intrusion Detection and Response. Workshop on Intrusion Detection and Prevention, 7th

ACM Conference on Computer Security, Athens, November 2000.

7. U. Lindqvist and E. Jonsson. How to systematically classify computer security intrusions.

Proceedings of the IEEE Symposium on Research in Security and Privacy, Oakland CA,

May 1997.

8. S. Northcutt and J. Novak. Network Intrusion Detection, QUE, 3rd Edition, August 2002.

9. R.S. Pathak. Integral Transforms of Generalized Functions and Their Applications. Taylor

& Francis, December 1997.

10. T.R. Peltier. Information Security Risk Analysis, Auerbach Pub., 1st. edition, January 2001.

11. J.K. Tudor. Information Security Architecture: An Integrated Approach to Security in the

Organization, CRC Press, September 2000.

12. H. Wei, D. Frinke, O. Carter and C. Ritter. Cost-Beneﬁt Analysis for Network Intrusion De-

tection Systems, CSI 28th Annual Computer Security Conference, Washington D.C., October

2001.