Ordering
in Mobile Networks Using Integrated
Sequencers
?
Sven Bittner
Institute of Computer Science, Freie Universit
¨
at Berlin
14195 Berlin, Germany
Abstract. Distributed applications mostly interact by exchanging messages. For
this purpose the messages often need to be ordered. Since today more and more
mobile devices are used message ordering in mobile networks is increasingly
important. Most ordering protocols for mobile networks use vector clocks or ma-
trices. In static networks often multicast trees ensure message ordering. In this
paper we propose a multicast protocol which ensures total order in a mobile envi-
ronment. It uses sequencers organized in a tree-structure to obtain this total order,
and introduces no extra-cost. This is because sequencers form no additional part
of the network, in fact they are integrated and embedded network components.
1 Introduction
Message ordering is needed in nearly all distributed applications, such as object repli-
cation, CSCW systems, or distributed monitoring. With advanced use of mobile devices
such applications are more and more expanded to mobile environments. For wired net-
works several multicast delivery algorithms are based on trees, such as CBT [?] and
PIM [?]. In fact they are only used for delivering multicasts and not for ordering. Also
they do not contain elements for handling mobility (e.g. handling handoffs). Without
such techniques dynamic networks are impossible, so algorithms are restricted to static
communication infrastructures. However multicast trees are an excellent structure to be
used for message delivery and they can be combined with ideas of sequencers. In the
following we present an ordering approach based on multicast trees and sequencers for
both message delivery and ordering usable in mobile environments.
The paper is organized as follows: Section 2 introduces the general system and the
proposed model. The algorithm is presented in Sect. 3. In subsections of Sect. 3 we
specify algorithms for causal and total order, dynamic groups and handoffs, and we
sketch a correctness proof. Section 4 pictures results of a performance evaluation. Re-
lated work is shown in Sect. 5. Conclusions and future work can be found in Section 6.
2 Concepts and System Model
The mobile network we assume is represented by 2 kinds of nodes: mobile hosts (MH)
denoted as h
x
and mobile support stations (MSS) denoted as S
x
. Mobile hosts h
x
are
?
This
work has been supported by the German Research Foundation (DFG) in the context of
the priority program (SPP) no. 1140.
Bittner S. (2004).
Ordering in Mobile Networks Using Integrated Sequencers.
In Proceedings of the 3rd International Workshop on Wireless Information Systems, pages 73-80
DOI: 10.5220/0002662100730080
Copyright
c
 SciTePress

connected by a wireless link to exactly one MSS, which is called local MSS denoted as
S(h
x
). We assume connections as reliable and FIFO. Messages from h
x
to h
y
can only
be delivered via their local MSSs. The set of all MHs is denoted as H = {h
1
, h
2
, ...}.
MHs with the MSS S
x
as local MSS are denoted as H(S
x
) = {h
x
∈ H|S(h
x
) = S
x
}.
MSSs are connected by an arbitrary wired network. Out of it we built a connected
acyclic undirected graph G = (S, E) as an overlay network in the application layer.
S = {S
1
, S
2
, ...} means the set of all MSSs, E is the set of edges (connections). The
neighbors of S
x
are called N (S
x
) = {S
y
∈ S|(S
x
, S
y
) ∈ E}. The property of an
acyclic graph is no restriction and introduces no problems concerning the network par-
tition in case of any link errors: A path between each pair of nodes is found as long as
any connection in physical links exists. Typically, the wired network has a high band-
width and a low propagation delay. Connections are also assumed as reliable and FIFO.
Online MHs h
x
∈ H are members of several multicast groups (MG) G(h
x
). For all
g
x
∈ G(h
x
) MH h
x
receives all messages sent to g
x
and vice versa it can send messages
to g
x
. This assumption is called closed groups in literature [?]. The set of MGs all
h
x
∈ H(S
x
) are members of is denoted by G(S
x
) =
S
h
x
∈H(S
x
)
G(h
x
). The set of
MGs the MHs of MSSs M ⊆ S are members of is defined by G(M) =
S
S
x
∈M
G(S
x
).
As defined by Lamport’s happend before relation [?] (denoted by →) message
m
x
causally precedes all messages m
y
for which holds m
x
→ m
y
. Multiple group
causal ordering (which is considered in this paper) is obtained if the former applies to
messages across groups. So if m
x
∈ g
x
∧ m
y
∈ g
y
∧ g
x
6= g
y
∧ m
x
→ m
y
then for
all MHs which are members of both groups, m
x
is delivered before m
y
. Single group
total ordering means that messages of each MG g
x
are delivered in the same order to all
members of g
x
. That definition of total order is regarded in this paper.
3 Algorithm
Our algorithm uses a sequencer-based approach to obtain total order. Unlike other pro-
posals [?,?,?] our sequencers do not cause extra-costs in delivering multicasts. So the
sequencers are no additional parts of the network, in fact they are integrated and em-
bedded components. Our algorithm works as follows: To send a multicast h
x
sends a
multicast message to S(h
x
). Then S(h
x
) delivers this message to all other MSSs which
again deliver the message to their MHs (including the sender). All S
x
∈ S know the
participants of all MGs among H(S
x
). Also MSSs exchange information about MHs
with other MSSs by exchanging G(S
x
) and G(N (S
x
)) with all neighbors N (S
x
). Ac-
cording to that information MSSs deliver multicast messages to neighbors and MHs.
This is shown in Fig. 1. 6 MSSs and 4 MHs are illustrated. MH h
1
is e.g. member of
MGs g
1
and g
3
. S
3
forwards multicasts of group g
1
to S
1
and S
4
, multicasts of groups
g
2
and g
3
to S
1
and multicasts of g
4
to S
4
. This information about forwarding is updated
by MSSs in case of changes. So each MSS can forward multicasts of g
x
to all MHs of
g
x
and to all MSSs with respective MHs in their subtrees. Therefore only information
about connected MHs and neighbor MSSs is required.
Causal Order.
Causal order is a side effect from the tree-based overlay network struc-
ture used and the assumption of FIFO message exchange between links. We can ob-
74

S
1
S
5
S
6
S
3
S
4
S
2
h
1
h
3
h
4
h
2
{g
1
, g
3
}
{g
1
, g
4
}
{g
1
, g
2
}
{g
1
, g
4
}
©
g
1,2,3,4
: S
3
ª
©
g
1,2,3,4
: S
4
ª
(
g
1
: S
3
, h
1,2
g
2,3
: h
1,2
g
4
: S
3
)
(
g
1
: S
3
, h
3,4
g
2,3
: S
3
g
4
: h
3,4
)
©
g
1,2,3,4
: S
4
ª
(
g
1
: S
1,4
g
2,3
: S
1
g
4
: S
4
)
Fig.1. Overview of topology, group memberships, and forwarding information
tain causal order with the characteristic that messages in MSSs are handled in order of
their arrival. The informal explanation for ensuring causal order is that if message m
x
causally precedes message m
y
in any MH h
x
∈ H then m
x
is delivered to each MH
before m
y
. That is due to handling messages in order of their arrival, the assumption of
FIFO and the fact that there is a unique path in overlay network for messages of 1 MH
to all other MHs. That also holds for messages of different groups in all MHs that are
members of both of these groups. A more detailed correctness proof can be found later.
Total Order. To obtain total order with respect to each group we use a sequencer for
each group. The sequencer is any MSS in the network. Each MSS knows in which
directions the sequencers can be found for all MGs. That knowledge of sequencers is
achieved by exchanging messages with neighbors. To multicast a message m
x
MH h
x
sends m
x
to its local MSS S(h
x
) that is sending the multicast in direction of MSS S
x
acting as sequencer. When the message is delivered to sequencer S
x
by MSS S
y
the
order of arrival of multicasts at S
x
is the total order for that group g
x
. Then S
x
sends
the multicast to all neighbors except the source N (S
x
) \ {S
y
} with a label that the
multicast is ordered now. So it can be directly delivered by MSSs in that subtree to their
MHs of group g
x
. S
x
also sends this multicast in direction of its source S
y
. There and
in the whole subtree that multicast is also delivered to all members of MG g
x
.
Moving the Sequencer.
To minimize the extra cost of multicast delivery a sequencer
has to be located in a central network position with respect to the MHs participating in
its MGs. At startup an arbitrary S
x
is used as sequencer for group g
x
. When multicasts
are sent S
x
counts the number of multicasts which have arrived from each neighbor and
connected MHs. If from a neighbor S
z
more multicasts for group g
x
arrive than from the
sum of the multicasts of group g
x
of the connected MHs and all other neighbors N (S
x
)\
{S
z
} then the sequencer should move into direction of S
z
in the overlay network. To
prevent frequent location changes we can multiply the former sum with a factor greater
than 1.0. Additionally, we allow location changes only after a certain amount of time.
That movement of the sequencer from S
x
to S
z
happens as an atomic operation to other
nodes (MHs and S \ {S
x
, S
z
}). It can be easily realized with that procedure: S
x
sends
takeOver(g
x
) to S
z
. When takeOver(g
x
) arrives at S
z
it replies takenOver(g
x
) and
75

waits for an ok(g
x
) from S
x
. Now only messages from S
x
are handled by S
z
(and never
send back to S
x
because S
x
is still the sequencer), messages from other neighbor MSSs
are queued. When takenOver(g
x
) arrives at S
x
it replies ok(g
x
). Then S
x
works as
normal MSS. When ok(g
x
) arrives at S
z
it acts as sequencer and handles all messages,
including queued ones. This ensures that the movement of sequencers is transparent to
other nodes. Other metrics and heuristics for placing sequencers can be found in [?].
To join the causal and the total order approach we have to introduce the following
concept: A multicast m
y
of group g
y
from MH h
x
can only be sent in direction of the
sequencer after any multicast m
x
of g
x
from h
x
with m
x
→ m
y
∧ g
x
6= g
y
has already
been delivered to h
x
. That can be implemented in local MSSs transparent to MHs.
Dynamic Groups.
If a MH changes its MGs or goes offline/online MSSs update their
information G(S
x
) and G(N (S
x
)). If no MH connected to S
x
is member of a group g
x
anymore (g
x
/∈ G(S
x
)) and messages of g
x
have at most be forwarded to neighbor S
y
in direction of sequencer of g
x
then neighbors N (S
x
) do not send messages related to
that group in future (sets G(S
x
) are updated in N (S
x
)) to S
x
. If a MSS S
x
is newly
interested in a group (that means g
x
/∈ G(S
x
) ∧ g
x
/∈ G(N (S
x
) \ {S
y
})) S
x
is sending
a ping(g
x
) message in the direction of the current sequencer. That message is delivered
as ordinary multicast messages. When a MSS interested in g
x
is met or the sequencer
is reached a pong(g
x
) message is replied to the sender. When that pong(g
x
) arrives at
S
x
it can inform the source MH that from now on all multicast messages are delivered
(all MSSs on the way to the sequencer realized the group membership because of the
unique path to the sequencer and the frequent update of information regarding MGs).
Handling Handoffs.
To handle handoffs, ensure correct delivery order and cause no
message losses we have to introduce the following handoff procedure: Consider that
h
x
moves from S
x
to S
y
. First h
x
registers all MGs G(h
x
) at S
y
. So S
y
sends ping
messages to all sequencers of groups {g
x
∈ G(h
x
)|g
x
/∈ G(S
y
)} and receives respective
pong messages. If all pong messages have arrived (or G(h
x
) ⊆ G(S
y
)) S
y
still does
not deliver messages of those groups to h
x
, instead it only stores them. Furthermore an
adopt(h
x
) message is sent to S
x
. When adopt(h
x
) is delivered to S
x
it stops forwarding
multicasts to h
x
and sends a relased(h
x
) message to the new local MSS S
y
. That
message also contains the identifications from last sent messages of all groups g
x
∈
G(h
x
). Then S
x
acts as in the case if h
x
leaves all groups G(h
x
). When relased(h
x
)
arrives at S
y
it discards all stored messages of corresponding groups less or equal then
the received identifications and delivers the remaining messages in order of receiving.
Correctness Proof. Now we prove the correctness of our algorithm. In the following
we will show that the algorithm delivers in causal order between groups and in total
order within single groups. Each message is delivered exactly once (safety) and after a
finite amount of time (liveness). We only show sketch-proofs because of limited space.
Proof (safety property, causal order). Suppose messages m
x
and m
y
, such that m
x
→
m
y
holds and m
x
∈ g
x
∧ m
y
∈ g
y
. Let m
y
be sent by h
y
. If m
x
→ m
y
then h
y
has
received m
x
before sending m
y
. So causal delivery in h
y
is proven. Suppose that m
y
is
76

delivered first in any h
x
. So there is a shorter path from S(h
y
) to h
x
than m
x
has taken.
That is a contradiction to the tree-structure and FIFO message exchange. ut
Proof (safety property, total order). Suppose messages m
x
∈ g
x
and m
y
∈ g
x
and
m
x
is delivered before m
y
in any MH h
x
. Suppose m
y
is delivered before m
x
in any
MH h
y
∈ H \ {h
x
}. That means there is a shorter path from the sequencer to h
y
in
case of delivering m
y
then in case of delivering m
x
. So we have a contradiction to the
tree-structure used and the FIFO message exchange. ut
Proof
(liveness property). Links between all network nodes support reliable message
exchange. There is only a bounded number of messages to be handled at each MSS
(unmarked multicast messages are spread away from sender and the unique sequencer
spreads these messages further away and back to sender). Thus, assuming each handling
takes a bounded time, each message is delivered after a finite amount of time. ut
4 Performance Evaluation
We have evaluated the performance of the main algorithm (total order using the de-
scribed approach) using a simulation on OMNeT++ [?]. The used network parameters
are shown in Table 1. We want to evaluate the performance of the network of MSSs, so
propagation delay and bandwidth of wireless links are neglected. We also use only one
MG. Our results describe the hypothetical maximum number of processable multicasts.
Using a real mobile network protocol, such as GPRS [?], there are technical limits:
Assuming 56 kbit/s downstream and a message size of 100 byte the maximum number
of multicasts per second without buffering is approx. 560. But with our hypothetical
number we obtain information about the behavior of the connecting network. We also
recognize limitations and can derive the behavior in complex cases, such as more MGs.
In the experiments we evaluate the influence of several parameters on the average
network traffic per multicast and processing time per multicast (time per multicast =
reciprocal value of the average number of processable multicasts). Here we plot time
per multicast. We assume an equal distribution of multicasts between MHs. Also an
equal distribution of MHs to MSSs and a symmetric network topology is assumed,
which is shown in Fig. 2 with the density parameter σ = 3 (number of subordinate
MSSs) and 4 levels of MSSs. In the following subsections we describe the evaluation of
the influence of the number of MSSs, number of MHs, and the location of sequencers.
Number of MSS.
When the number of MSSs is increased the average time to deliver a
multicast should decrease significantly. The network traffic per multicast should differ
only to a small extend because the main load is produced by the delivery of multicasts
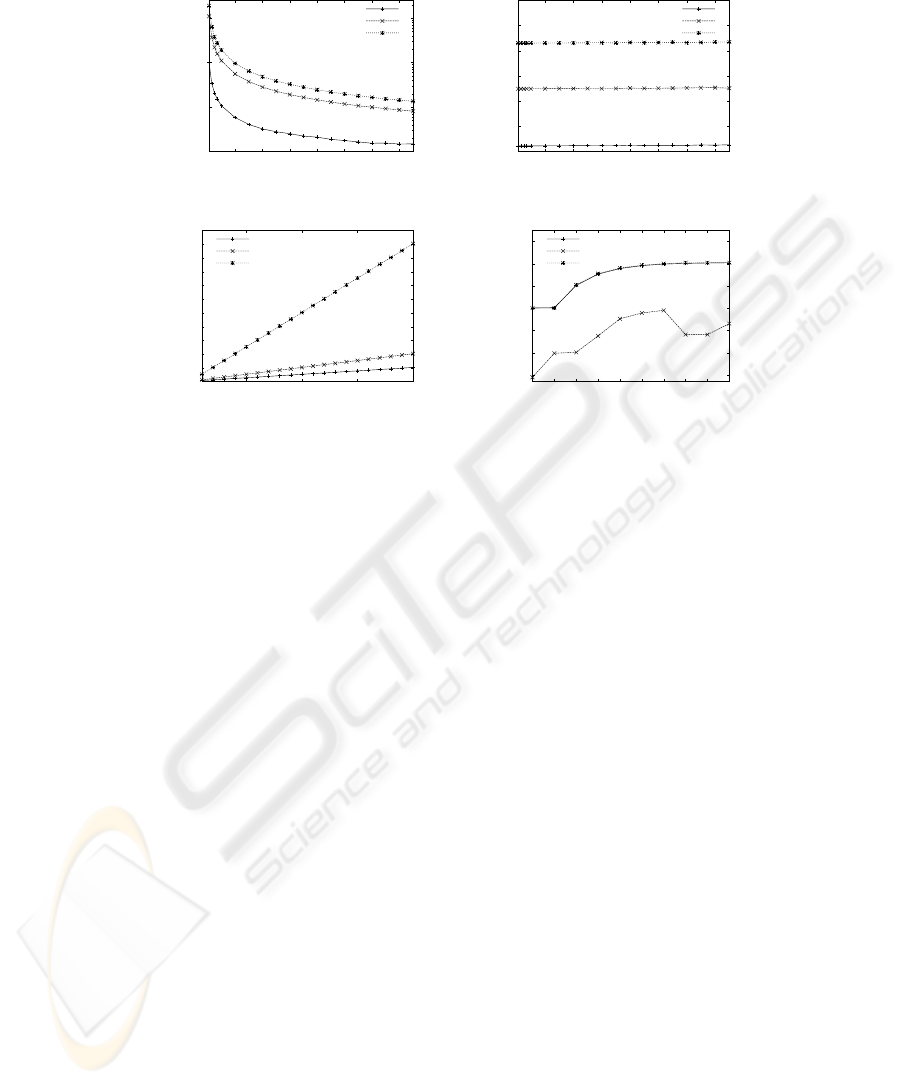
to MHs. The influence on time and network load per multicast is shown in Fig. 3(a), (b).
In the experiments we choose 3 different settings. The sequencer is the central network
node, the density parameter is chosen with σ = 3. We vary the number of MSSs from 1
to 150. As expected the time per multicast decreases significantly (logarithmic scale in
Fig. 3(a)) if the number of MSSs grows. Using 150 MSSs the delivery time is approx.
67 to 136 times faster than using 1 MSS. Adding more MSSs means only a very low
increment of network traffic. The graph shows almost constant network load, because
delivery to the MHs is really more crucial than communication among the MSSs.
77

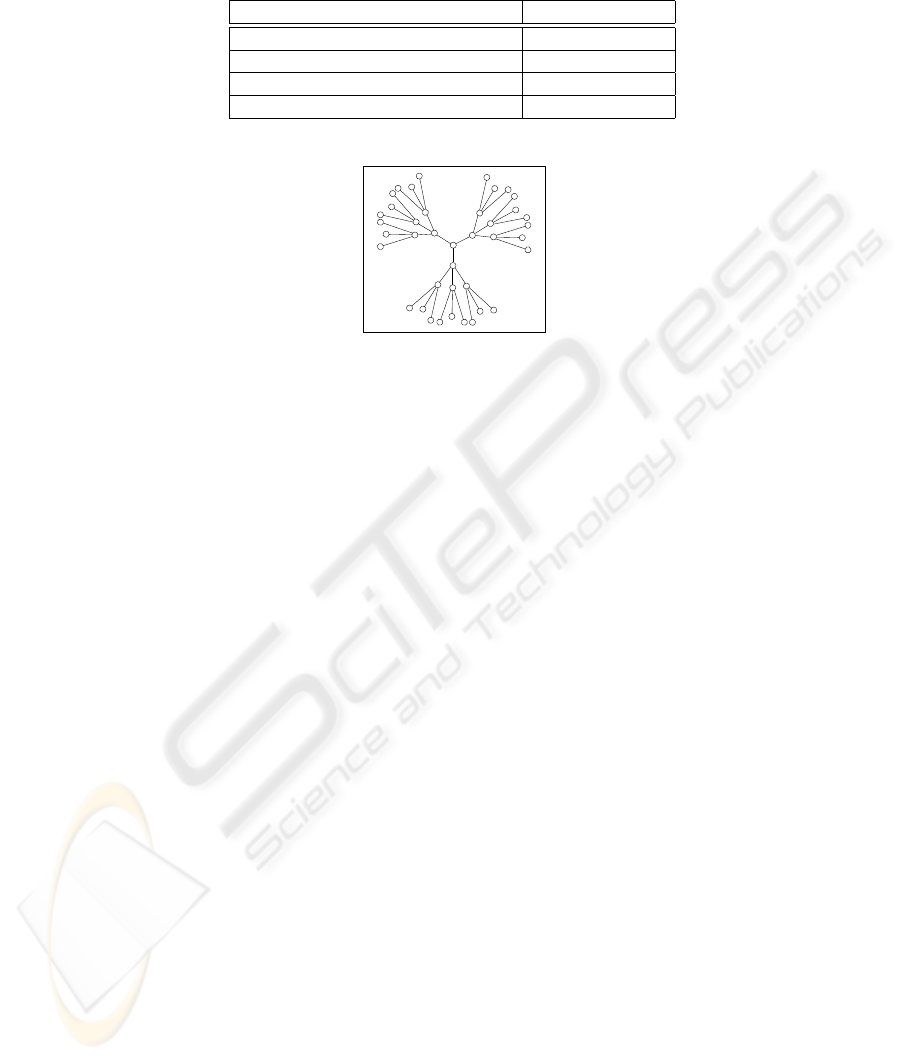
Table 1. Overview of network parameter dimensions used
Parameter
Chosen setting
number of MSSs/MHs
1 to 1,023/1,000 to 20,000
data rate/propagation delay wired links
100 mbit/s / 0.5 ms
computation delay en-/decapsulate/serve a message
0.1 / 0.1 / 0.2 ms
size of multicast message (user data)
100 byte
Fig.2. Symmetric network used in experiments with σ = 3 and 4 levels of MSS
Number of MH.
With a growing number of MHs the network traffic and the time per
multicast should increase. That is shown in Fig. 3(c) using different numbers of MSSs.
A density parameter σ = 3 is used in this experiment. We evaluate 1,000 to 20,000
MHs. Here we only plot the average time per multicast. The network traffic is a straight
line from approx. 120 kB to 2,3 MB. The time per multicast linearly increases with a
growing number of MHs. That is because each MH introduces a constant amount of
extra work for MSSs. Using 10 MSSs the time per multicast is approx. 12 times higher
when using 20 times more MHs, in case of 100 MSSs the time is 19 times higher.
Location of Sequencer.
A main assumption for our algorithm is that a movement
of sequencers influence the average time per multicast. If a sequencer is in a central
position according to the MHs of its group the time per multicast should be smallest.
In our experiments we choose a setting with 1,023 MSSs and σ = 2. So we have a
symmetric network with 10 levels of MSSs. 5 MHs per MSS have been connected in
experiments. We evaluate the time per multicast in 3 cases: (all) - MHs are connected
to all MSSs, (outer) - MHs on outer level, (inner) - MHs on 7 inner levels. Figure 3(d)
shows the average time per multicast. The best performance is achieved in case (outer).
There approx. 4 times as much MHs are members of the same MG as in case (inner),
but the time per multicast is much lower. The reason is that inner MSSs are not involved
in delivering multicasts to MHs but only to MSSs. In case (inner) we can see opposite
results: Even if there are 8 times less MHs as in case (all) approx. the same number of
multicasts is delivered (inner MSSs always have same high load). In all 3 cases we can
observe that a central position of the sequencer means lower times per multicast. In our
experiments the increase of performance goes up to 21%. The traffic is not shown: We
have nearly constant load with the highest in case (all), followed by (outer) and (inner).
78

0.001
0.01
0.1
1
1 20 40 60 80 100 120 140
Time per multicast in seconds
Number of MSSs
1000 MHs
11000 MHs
19000 MHs
0
500
1000
1500
2000
2500
3000
1 20 40 60 80 100 120 140
Network traffic per multicast in kB
Number of MSSs
1000 MHs
11000 MHs
19000 MHs
(a) Time dependent on no. of MSSs (b) Network load dependent on no. of MSSs
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0.22
1000 5000 10000 15000 20000
Time per multicast in seconds
Number of MHs
10 MSSs
50 MSSs
100 MSSs
0.0009
0.001
0.0011
0.0012
0.0013
0.0014
0.0015
1 2 3 4 5 6 7 8 9 10
Time per multicast in seconds
Level of sequencer
all
outer
inner
(c) Time dependent on no. of MHs (d) Time dependent location of sequencer
Fig.3. Influence on algorithm dependent on no. of MSSs/no. of MHs/location of sequencer
5 Related Work
There are some multicast protocols using a tree-approach: Core Based Trees (CBT) [?],
the Protocol Independent Multicast (PIM) [?] and also the Border Gateway Multicast
Protocol (BGMP) [?] can be found. All these protocols construct propagation trees for
MGs. Messages are sent towards the root. The roots do not adapt to network changes.
But these protocols are only involved in propagating a multicast and not in ordering. For
sequencer ordering there exist mainly 3 approaches: The first is to ask the sequencer
for a sequence number and send a message with that number (e.g. implemented by
Armstrong et al. [?]). Another idea is to multicast to group members and the sequencer.
Then sequencers also send messages determining the order (e.g. realized by Birman et
al. [?]). And the last is to send a multicast to the sequencer, which forwards to all group
members (e.g. done by Navaratnam [?]). That idea is also considered in our approach
with the improvement that sequencers are embedded parts of the delivery tree and there
is no overhead in both delivery time and network traffic. Nevertheless mobility is not
considered in those protocols [?,?,?]. Order protocols dealing with mobility use vector
clocks or matrices, such as [?,?]. Or they use coordinators [?] normally not involved in
communication to obtain order, indeed they are a system’s bottleneck.
79

6 Conclusions & Future Work
We have presented a new approach for a sequencer-based ordering of multicasts in mo-
bile networks. We obtain total order of the multicasts in one multicast group and causal
order for messages across groups. Our approach chooses an arbitrary MSS as sequencer
in the beginning. Then, according to the behavior of MHs the sequencer moves within
the network to minimize the distance to MHs of its group. The sequencer is placed in a
propagation tree of multicast messages so there is no extra cost for ordering messages
via a sequencer. In fact sequencers are integrated and embedded network components
which forward messages in any case. We have also proposed algorithms for dynamic
group changes and a handoff procedure for changing local MSSs.
We have simulated the performance of our approach by evaluating influences of
different parameters. With this simulation we have shown that a sequencer should be
located in a central position within the network according to MHs participating in its
group. So we can increase processable multicasts and decrease network traffic. We have
also shown the influence of the quantity of MSSs and MHs. In future we want to eval-
uate the performance of the proposed handoff procedure and the overhead of the se-
quencer movement itself.
80