Application of Fractal Codes in Recognition of Isolated

Handwritten Farsi/Arabic Characters and Numerals

Saeed Mozaffari

, Karim Faez

, Hamidreza Rashidy Kanan

Electrical Engineering Department, AmirKabir University of Technology, Hafez Avenue,

Tehran, Iran, 15914

Abstract. In this paper we proposed a new method for isolated handwritten

Farsi/Arabic characters and numerals recognition using fractal codes. Fractal

codes represent affine transformations which when iteratively applied to the

range-domain pairs in an arbitrary initial image, the result is close to the given

image. Each fractal code consists of six parameters such as corresponding do-

main coordinates for each range block, brightness offset and an affine trans-

formation which are used as inputs for a multilayer perceptron neural network

for learning and identifying an input. This method is robust to scale and frame

size changes.32 Farsi’s characters are categorized to 8 different classes in

which the characters are very similar to each others. There are ten digits in

Farsi/Arabic language and since two of them are not used in postal codes in

Iran, therefore 8 more classes are needed for digits. According to experimental

results, classification rates of 91.37% and 87.26% were obtained for digits and

characters respectively on the test sets gathered from various people with dif-

ferent educational background and different ages.

1 Introduction

English, Chinese and Kanji isolated handwritten character recognition have long been

a focus of study, but a little researches have been done on Farsi and Arabic. Some

previous works on recognition of isolated characters, words and scripts of Farsi and

Arabic language have used some structural features [1] [2] and moment features

[3].Fractal theory has been used in several areas of image processing and computer

vision. In this method, similarity between different parts of an image is used for rep-

resenting of an image by a set of contractive transforms on the space of images, for

which the fixed point is closed to the original image. This concept has been used

recently by some researchers for face recognition [4] [5]. In the case of character

recognition, we deal with the image of characters, and by using features that are ex-

tracted from the original image, the process of classification can be more facilitated.

In this study we used fractal codes as features in the recognition process and fed them

as inputs to a multilayer perceptron neural network for learning and identifying char-

acters. As fractal codes are so sensitive to translation, scaling and rotation, some

Mozaffari S., Faez K. and Rashidy Kanan H. (2004).

Application of Fractal Codes in Recognition of Isolated Handwritten Farsi/Arabic Characters and Numerals.

In Proceedings of the 4th International Workshop on Pattern Recognition in Information Systems, pages 202-209

DOI: 10.5220/0002662802020209

 SciTePress

preprocessing has been required. Location invariancy and scale normalization is

achieved by finding the bounding rectangle of each character and scaling it to a

×64 pixel image. The learning and test sets were gathered from various people

with different educational background and different ages.32 Farsi’s characters are

categorized to 8 different classes based on the similarity of the characters in each

class. There are ten digits in Farsi/Arabic language that two of them are not used in

the postal codes in Iran. So digits can be categorized in 8 different more classes. A

multilayer perceptron (MLP) neural network is used as a classifier which includes

one hidden layer, 64 input nodes and 8 output nodes. The Overall classification rate

for 8 classes of characters and 8 classes of numerals were 87.26% and 91.37% re-

spectively. This paper is organized as follows. Section 2 describes the basic concepts

in fractal encoding consisting of preprocessing phase followed by feature extraction

from fractal-coded images. The experimental results are presented in section 3. Fi-

nally the conclusion remarks are given in section 4.

2. Feature Extraction

2.1 Pre-Processing

For a given binary image containing a single character or numeral, three pre-

processing tasks are needed to make the system invariant to scale changes, frame size

changes and rotation. To remove any differences due to location of character or nu-

meral within the image, the bounding rectangle box of each character or numeral is

found. Then this bounding box is scaled to 64

64 pixel image, for scale normaliza-

tion.

2.2 Overview of Fractal Image Coding

With the advent of information age, the need for mass information storage and re-

trieval growed. Different image compression methods have been focused for a long

time to reduce this massive information, but a novel promising approach called fractal

image coding has drawn much attention recently. The fundamental principles of frac-

tal coding consist of the representation of any image by a contractive transform of

which the fixed point is to close to the original image. A transform

is said to be

contractive if for any two points

the distance between them satisfy equation

(1) for some s<1.

, pp

)2,1())2(),1(( ppdspwpwd

(1)

Banach’s fixed point theorem guarantees that, within a complete metric space, the

fixed point of such a transformation may be recovered by an iterated application,

thereof to an arbitrary initial element of that space [6]. Fractal encoding is based on

the concepts and mathematical results of iterated function systems (IFS). Fractal com-

pression became a practical reality with the introduction by Jacquin of the partitioned

IFS (PIFS), which differs from an IFS in that each of the individual mappings oper-

ates on a subset of the image, rather than on the entire image [7]. An image to be

203

encoded is partitioned into non-overlapping range blocks R with the size and

overlapping

domain blocks D with the size

NN ×

NN 22

as depicted in Fig.1. The task of

fractal encoder is to find a D block in the same image for every R block such that

transformation of this domain block

minimize the collage error in equation(2).

Distances are usually measured by mean square error (MSE), since optimization of

the standard block mappings is simple under this measurement [7].

)(DW

)(min

DWRErrorCollage −=

(2)

Suppose we are dealing with a

6464

binary image in witch each pixel can have

one of 256 levels (ranging from black to white). Let

be pixel

non- overlapping sub-squares of the image, and let D be the collection of all

pixel overlapping sub-squares of the image. The collection D contains

squares. For each

block, search through all of D blocks to find a which

minimizes equation (2). There are 8 ways to map one square onto another. The square

can be rotated to 4 orientations or flipped and rotated into 4 other orientations which

are depicted in Fig.2. Having 8 different affine transformations, it means comparing

squares with each of the 256 range squares.

25621

,.....,, RRR

44×

88×

32495757 =×

R DD

∈

2599232498 =×

Fig.1. One of the block mappings in PIFS representation

1 2 2 1 3 1 1 3

3 4 4 3 4 2 2 4

4 3 3 4 2 4 4 2

2 1 1 2 1 3 3 1

Fig.2. 8 different ways to map one square onto another

As mentioned before, a

block has 4 times as many pixels as an , so we must

either subsample (choose 1 from each

sub-square of ) or average the

sub-squares corresponding to each pixel of

when we minimize equation (2) [8].

Minimizing equation (2) means two things. First it means finding a good choice

22×

204

for . Second, it means finding a good contrast and brightness setting and for

in equation (3).

(3)

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

s00

0dc

0ba

Assume two squares containing

pixel intensities, for and

for . By minimizing equation (4), and can be obtained.

aaa ,.....,,

21 i

bbb ,......,,

21 i

R s o

(4)

∑

−+=

)boa.s(R

This will give us a contrast and brightness setting that makes the affinely trans-

formed

values have the least squared distance from the values. The minimum of

R occurs when the partial derivation respect to and are zero, which occurs when

s o

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

−=

∑∑∑∑∑

=====

)a(an/)b)(a()ba(ns

(5)

n/asbo

⎥

⎦

⎤

⎢

⎣

⎡

−=

∑∑

In this case,

n/)b2on(o)ao2)ba(2as(sbR

⎥

⎦

⎤

⎢

⎣

⎡

−++−+=

∑∑∑∑∑

=====

A choice of

, along with a corresponding and , determines a map . The

type of image partitioning used for the range blocks can be so different. A wide vari-

ety of partitions have been investigated, the majority being composed of rectangular

blocks. Different types of range block partitioning were described in [9]. In this re-

search we used the simplest possible range partition consists of the fixed size square

blocks, that is called fixed size square blocks (FSSB) partitioning.

2.3. Encoding Algorithm

The procedure for finding a fractal model for a given image is called encoding, com-

pression, or searching for a fractal image representation.Encoding algorithm can be

summarized as follow [10]:

1- Input the original binary image.

2- Partition the input image into R blocks according to FSSB partitioning scheme.

3- Create a list of D blocks.

4- Search for a fractal match. Given a

region, loop over all possible D blocks to

find the best match using a given metric. This is the most time consuming step of the

whole algorithm.

205

5- Select fractal elements. After finding the best match, fractal elements which are 6

real numbers are selected as follow:

a,b: (x,y) coordinates of the D block which is always pointed to the top-left corner of

the D block square.

c,d:(x,y) coordinates of the corresponding R block

e:The number of the affine ransformation that makes the best match.( a number be-

tween 1 and 8).

f: The intensity which is a number between 0 and 256.

2.4. Decoding Algorithm

The reverse process of generating an image from a fractal model is called decoding,

decomposition, or displaying a fractal format image. In the case of character recogni-

tion, although it is not necessary to decode the fractal models that are obtained from

previous section, we have done it to verify the validation of coding algorithm. Decod-

ing process starts with an arbitrary initial image that is a uniform gray level picture

with 128 intensities in our case. Then the decoding algorithm is iterated about 6 to 16

times. The results for different iterations and different R block sizes are depicted in

Fig.3 and Fig.4. After each iteration, the average of error and peak signal to noise

ratio(PSNR) are calculated according to equations (6) and (7). Table.1. shows these

results

jiJjiIerrorofaerage

−=

∑∑

])),(),(([

(6)

)

errorofaverage

255

log(20PSNR ×=

(7)

(a) (b) (c) (d)

Fig.3 decoding algorithm’s results for N=4

(a) original image (b) arbitrary initial image

(a) (b) (c) (d)

Fig.4 decoding algorithm’s results for N=8

(a) original image (b) decoded image after 1 iteration

206

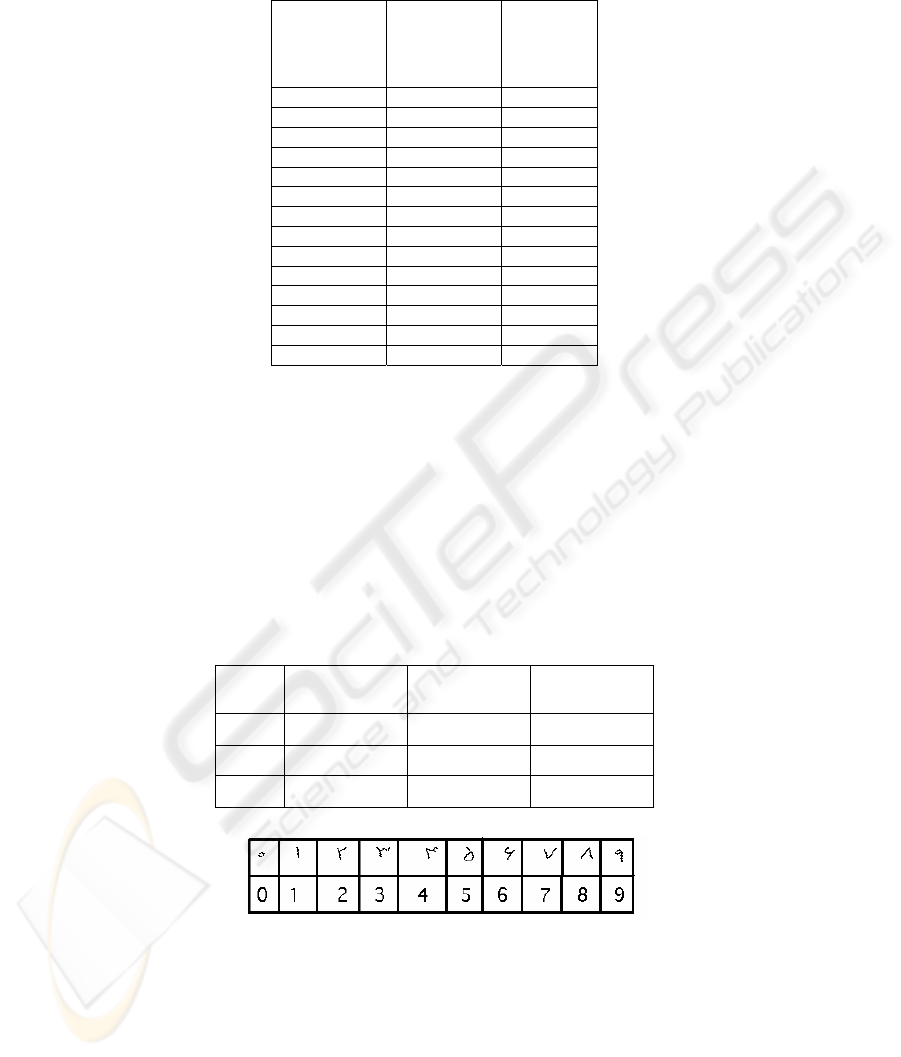
Table.1 Average of error and PSNR versus number of iteration

PSNR

(dB)

Average

Error

Number

Interation

40.32 2.45 0

42.30 1.95 1

44.06 1.59 2

45.53 1.38 3

46.69 1.18 4

47.55 1.06 5

48.16 0.99 6

48.57 0.95 7

48.84 0.92 8

49.02 0.90 9

49.14 0.89 10

49.21 0.88 11

49.26 0.87 12

49.34 0.86 15

With the increase in R blocks size, the PSNR and average of error decreases and

increases respectively, and also the decoding algorithm became faster. These results

are shown in Table.2.

3. Experimental Results

In Farsi language, there are ten digits that are shown in Fig.5. Because of similarity

between (0, 5) and ( 2 , 3) especially in handwritten text, digits (0) and (2) are not

used in postal codes in Iran. Thus, we have 8 different classes for digits.

Table.2. Encoding Results with different parameters

Encoding

Time (Sec)

Average Of

Error

PSNR (dB)

4 6.78 0.884 49.19

8 3.81 0.927 48.76

16 1.86 1.01 48.00

Fig.5. Digits in Farsi

Dots play an important rule in Farsi characters. For example as shown in Fig. 6,

there are four different characters that only differ in number of and the position of

dots. To simplify, we neglect these dots and consider characters in their main form

207

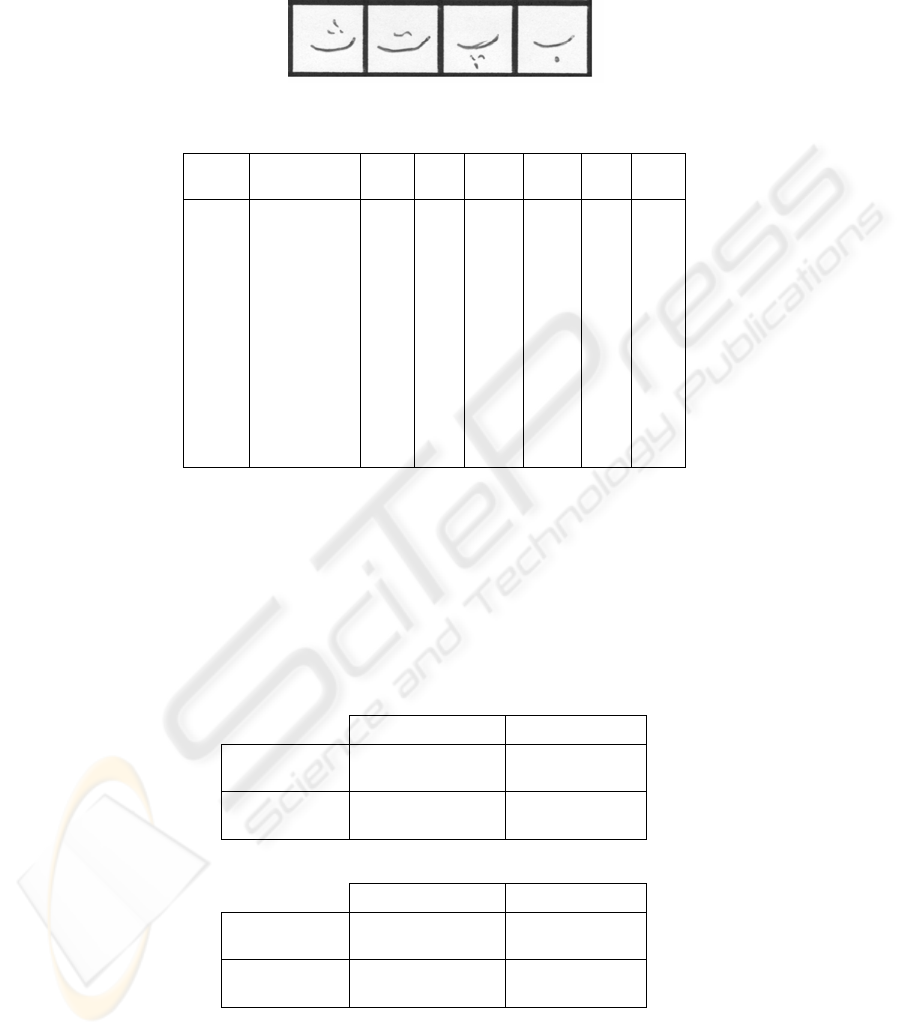
without the dots. We categorize Farsi characters into 8 different classes which are

shown in Table.3.

Fig.6. Four Farsi Characters with different dots and similar patterns

Table.3. Final character classes

1 2 3 4 5 6 7 8

ا ف ب ج د س ك م ﻩ

ط ق پ چ ذ ش گ

ظ ل ت ح ر ص

ن ث خ ز ض

ع ژ ي

غ و

Training and test sets, for characters and numerals, were gathered from more than

200 people with different educational background. Our database contains 480 sam-

ples per digit (total of 3840), and 190 samples per character (total of 6080). We have

used 100 samples of each character (total of 3200) for training and 90 samples (total

of 2880) for test. We also used 280 samples of each digit (total of 2240) for training

and 200 samples (total of 1600) for test. By using an MLP neural network as a classi-

fier, the recognition rate of 91.37% and 87.26% are achieved for digits and charac-

ters respectively. (see Table.4 and 5) .

Table.4. Classification results for characters

Correct% Error%

Training

Set

97.4%

(3117/3200)

2.6%

(83/3200)

Test Set

87.26%

(2785/3200)

12.74%

(415/3200)

Table.5. Classification results for digits

Correct% Error%

Training

Set

98%

(2196/2240)

(44/2240)

Test Set

91.37%

(2047/2240)

8.63%

(193/2240)

208

4. Conclusion

In this research we have used fractal codes as features for Farsi digits and charac-

ters. By using an MLP neural network as a classifier, fair recognition rates are ob-

tained. As we are aware, this is the first research in OCR which uses fractal codes as

features, so using other partitioning methods such as quadtree may lead to better

results.

References

1. R.Plamondon and S.N.Srihari”On-Line and Off-Line handwritten Recognition: A

comprehensive survey”. IEEE Trans on Pattern Analysis and Machine Intelli-

gence ,Vol.22,No.1,January 2000,pp.63-84

2. M.Dehghan, K.Faez, M.Ahmadi and M.Shridhar “Off-Line unconstrained Farsi

Handwritten Recognition Using Fuzzy Vector Quantization and hidden Markov

Word Models”.Proceeding of 15

International Conference on Pattern Recogni-

tion ,Vol.2,2000,pp.351-354.

3. I.S.I.Abuhiba, S.A.Mahmoud and R.G.Green “Recognition of handwritten cursive

Arabic characters” ,IEEE Trans on Pattern Analysis and Machine Intelli-

gence.Vol.16,No.6, June 1994,PP.664-672.

4. P.Temdee, D.Khawparisuth and K.Chamnongthai “Face Recognition by using

Fractal Encoding and Backpropagation Neural Network”,15

ISSPA ,Brisbane

,Australia, August,1999,PP,159-161.

5. H.Ebrahimpour,V.Chandran and S.Sridharan “Face Recognition Using Fractal

Codes” ,IEEE,2001,PP.58-61.

6. E.Kreyszing, ”Introductory Functional Analysis with applications”. New

York.Wiley, 1978.

7. Y.Fisher, ” Fractal Image Compression, Theory and Application”. Berlin, Ger-

many. Springer-Verlag.1995.

8. Yuval Fisher “Fractal Image Compression”, SIGGRAPH’92 Course Notes, Tech-

nion Israel Institute of Technology from The San Diego Super Computer Center,

University of California, San Diego

9. Brent Wohlberg and Gerhard Jager,” A Review of Fractal Image Coding Litera-

ture”, IEEE Transactions on Image Processing ,VOL 8,NO 12, December 1999.

10. Ning Lu,”Fractal Imaging”, Academic Press, June 1997.

209