Generalized Policy Support System and

Its Hierarchy Semantics

Yibing Kong, Janusz R. Getta, Ping Yu, and Jennifer Seberry

School of Information Technology and Computer Science,

University of Wollongong,

Wollongong, NSW, Australia

Abstract. One common characteristic of many Policy Support Systems (PSSs)

is their dependency on the concept of hierarchy. Hierarchy does not need to be

limited to a hierarchy of roles (subject centric) as in traditional Role-Based Ac-

cess Control (RBAC). Instead, it can be applied to other aspects of PSS such as

object, environment, purpose and so on. In this paper, we propose a new general-

ized model for PSS. The model uniﬁes Generalized Role-Based Access Control

(GRBAC) and Enterprise Privacy Practices (E-P3P) policy support systems and

generalizes their hierarchy semantics.

Keywords: Access Control, Hierarchy, Hierarchy Semantics

1 Introduction

Organizations must enforce data protection policies to secure data collected and gen-

erated during their daily operational procedures. At a conceptual level, data protection

polices are expressed as sequences of statements written in a natural language. In the

past, the enforcement of data protection policies was based on manual work or inﬂexible

mechanisms such as Discretionary Access Control (DAC), Mandatory Access Control

(MAC) models. The emerge of Role-Based Access Control (RBAC) model improved

efﬁciency of data protection. Unfortunately, RBAC model is still not expressive enough

to efﬁciently and effectively enforce more sophisticated data protection policies in an

organization. Recently more powerful systems have appeared; Generalized Role-Based

Access Control (GRBAC) [1] and Enterprise Privacy Practices (E-P3P) [2] are repre-

sentatives of such systems.

GRBAC, proposed by Moyer and Ahamad in [1], is an extension of traditional

RBAC. It generalizes the classical concept of role through the new concepts such as

subject role, object role and environment role. These concepts are used to structure the

subjects (users), objects (data) and environments (conditions). With these new types of

roles, GRBAC is capable of creating rich access control policies. GRBAC provides an

algorithm to enforce the access control policies deﬁned in the model. E-P3P, developed

by Ashley et al. in [2], has a well-deﬁned privacy architecture and semantics. It enables

an organization to express its privacy policies in E-P3P format and to enforce the poli-

cies automatically. We shall call these two systems as Policy Support Systems (PSSs)

because they are designed for expressing and enforcing data protection policies.

Kong Y., R. Getta J., Yu P. and Seberry J. (2004).

A Generalized Policy Suppor t System and Its Hierarchy Semantics.

In Proceedings of the 2nd International Workshop on Security in Information Systems, pages 136-145

DOI: 10.5220/0002667301360145

 SciTePress

A hierarchy is a partial order on a set of elements that deﬁnes a seniority relationship

between elements [3]. Hierarchy is not a new concept, it has been extensively studied

in the past. Role hierarchy [4–7] in role-based access control and hierarchy in Flexible

Authorization Framework (FAF) [8] are examples of such studies. Hierarchy semantics

is an inseparable part of hierarchy that deﬁnes rules of authorization propagation. Var-

ious hierarchy semantics was deﬁned in GRBAC and E-P3P. However, the hierarchy

semantics deﬁned is either incomplete or incorrect. In this paper, we propose a gener-

alized PSS model that covers GRBAC and E-P3P. Based on this model, the hierarchy

semantics of GRBAC and E-P3P is analyzed. We propose new hierarchy semantics to

solve the problems encountered in GRBAC and E-P3P.

The organization of the rest of the paper is as follows. Section 2 introduces the con-

cept of hierarchy. A generalized PSS is proposed in section 3 and hierarchy semantics

of GRBAC and E-P3P is analyzed in section 4. Section 5 presents new hierarchy se-

mantics. Finally, in section 6, we conclude the paper and outline the plans of future

research.

2 Deﬁnition of Hierarchy

A mathematical structure called hierarchy was deﬁned by Jajodia et al. in [8] as a triple

(X, Y, ≤), where X is the set of primitive entities, e.g. a user, an object; Y is the set of

categories, e.g. a group, an object type; ≤ is a partial order on (X ∪ Y ) such that each

x ∈ X is a minimal element of (X ∪Y ) ; an element x ∈ X is said to be minimal iff there

are no elements below it in the hierarchy, that is iff ∀y ∈ (X ∪ Y ) : y ≤ x ⇒ y = x.

This deﬁnition is rich enough to capture all hierarchy structures presented in [1, 2]. We

simplify this deﬁnition of hierarchy to a two-entry tuple (Y, ≤), i.e. H = (Y, ≤) where:

•

Y is the set of categories, such that a primitive entity is treated as a category of

itself, called primitive category. A primitive category contains one primitive en-

tity and the name of the category is the same as the name of the primitive entity.

For example a primitive entity James Bond belongs to a primitive category called

James Bond.

•

≤ is a partial order on Y such that each primitive category in Y is a minimal element

of Y .

In addition, we deﬁne the following two binary relations over Y . The ﬁrst binary

relation < describes descendant-ancestor relationship between the elements in Y . If

, y

∈ Y and y

< y

, y

is said to be the ancestor of y

; y

is said to be the descendant

of y

. The relation y

< y

is interpreted as y

is in the category of y

. For an element

, a set of all its ancestors is deﬁned as Aset

= {y

: y

∈ Y and y

< y

}; a set

of all its descendants is Dset

= {y

: y

∈ Y and y

< y

}. The second binary

relation <

describes child-parent relationship between elements in Y . If y

, y

∈ Y

and y

, y

is said to be the parent of y

; y

is said to be the child of y

. For an

element y

, a set of all its parents is deﬁned as P set

= {y

: y

∈ Y and y

};

a set of all its children is Cset

= {y

: y

∈ Y and y

Some of the hierarchies used in practice are listed as follows. Subject hierarchy

GH = (G, ≤

) where G is a set of groups (roles), ≤

deﬁnes hierarchy relationships

137

between groups in G. Object hierarchy T H = (T, ≤

) where T is a set of types,

≤

deﬁnes hierarchy relationships between types in T . Environment hierarchy EH =

(E, ≤

) where E is a set of environments, ≤

deﬁnes hierarchy relationships between

environments in E. Purpose hierarchy P H = (P, ≤

) where P is a set of purposes,

≤

deﬁnes hierarchy relationships between purposes in P .

3 A Generalized Model of a Policy Support System

It is common for a PSS to deﬁne more than one hierarchies. For example, GRBAC

[1] deﬁnes GH, T H and EH hierarchies and E-P3P [2] deﬁnes GH, T H and P H

hierarchies. Furthermore these systems deﬁne some sets of elements, such as the set

of actions, the set of obligations, the set of authorization types etc. In this section, we

deﬁne a generalized model which uniﬁes GRBAC and E-P3P.

A generalized Policy Support System PSS = (H, S, A, R, P), where:

•

H denotes a set of n hierarchies H

, ..., H

, n ≥ 1.

• S is a set of m sets S

, ..., S

, where m ≥ 0. The sets deﬁned in S provide ad-

ditional restrictions on PSS; for example the sets of obligations and conditions in

E-P3P system are instances of such sets. S is optional and its existence depends on

the designer of a PSS, e.g. in GRBAC S is absent.

•

A is a set of actions to be performed on data.

• R is a set of authorization types (rulings). R = {+, −, ⊕, ª, ¯, ⊗}, where +

means positive authorization; − means negative authorization; ⊕ means implicit

positive authorization; ª means implicit negative authorization; ¯ means autho-

rization pending and ⊗ means no authorization. + and − are used for explicit

authorization assignment through policy rules; ⊕ and ª are used for authorization

propagation; ¯ is used for conﬂicts resolution; ⊗ is used when none of the above

ﬁve rulings is applicable.

• P is a set of precedences over policy rules. P = Z, i.e. P is the set of integers that

determines precedence orders over a set of policy rules; the greater number denotes

the higher precedence. P is also optional; the absence of P means that all policy

rules have the same precedence.

The elements of the above ﬁve parts are used as basic units to form policy rules. The

collection of all the policy rules in a PSS is a policy rule set, denoted as Γ . A policy

rule γ ∈ Γ is a tuple (γ

, ..., γ

, γ

, ..., γ

, γ

) where

•

∈ H

or γ

= null (i.e. nothing is speciﬁed for γ

), where n ≥ i ≥ 1.

•

∈ S

or γ

= null, where m ≥ i ≥ 0.

•

∈ A is the action entry that speciﬁes the action to be performed.

•

∈ {+, −} is the ruling entry that speciﬁes either positive or negative authoriza-

tion.

•

∈ P is the precedence of γ.

138

It is possible to show that the model deﬁned above “includes” GRBAC [1] and

E-P3P [2]. A GRBAC system is a triple (H, A, R), where H = {GH, T H, EH}

(GH is subject hierarchy, T H is object hierarchy and EH is environment hierar-

chy). A GRBAC policy rule [1] is a tuple (S, O, E, op, permission bit), where S ∈

GH, O ∈ T H, E ∈ EH, op ∈ A and permission bit ∈ {+, −}. There is no prece-

dence over GRBAC policy rules, hence the set P is absent. An E-P3P system is a tuple

(H, S, A, R, P), where H = {GH, T H, P H}, S = {O, C} (GH is subject hierarchy,

T H is object hierarchy, P H is purpose hierarchy, O is the set of obligations and C is

the set of conditions). An E-P3P policy rule [2] is a tuple (i, t, p, u, r, a,

c), inside

which i ∈ P, t ∈ T H, p ∈ P H, u ∈ GH , r ∈ {+, −}, a ∈ A,

o ∈ O and

c ∈ C.

According to the deﬁnition of a policy rule, an access request α can be expressed

as α = (α

, ..., α

, α

, ..., α

, α

) where α

∈ H

or α

= null, n ≥ i ≥ 1;

∈ S

or α

= null, m ≥ i ≥ 0; α

∈ A. A set of policy rules Γ

is used

to validate α, where Γ

⊆ Γ . All policy rules in Γ

are called matching rules of α.

Matching rules must satisfy the following properties:

• ∀γ ∈ Γ

, α

≤ γ

, where n ≥ i ≥ 1.

• ∀γ ∈ Γ

, γ

= α

, where m ≥ i ≥ 0.

•

∀γ ∈ Γ

, γ

= α

The validation of α in Γ

consists of n sub-validations from α

to α

. That is,

∀α

∈ α where n ≥ i ≥ 1, α

needs to be validated according to the matching rule

set Γ

whether α

is authorized for α

. If and only if all of these hierarchy elements

are authorized for α

, α is granted.

∀γ ∈ Γ

, where γ = (γ

, ..., γ

, γ

, ..., γ

, γ

), we can assign a

tuple (γ

, γ

) to γ

, ..., γ

. An authorization of an element y ∈ H is a tuple

(ruling, precedence) inside which ruling ∈ R, precedence ∈ P; it is denoted as

where i is the index of the authorization. Due to the optional property of P, the

precedence entry of an authorization is also optional. The ruling entry of A

is denoted

as A

.ruling and the precedence entry of A

is denoted as A

.precedence. We call

an authorization explicitly deﬁned by policy rules explicit authorization; obviously for

an explicit authorization A, A.ruling ∈ {+, −}. Authorization may also be derived by

hierarchy semantics, we call a derived authorization implicit authorization; for an im-

plicit authorization A, A.ruling ∈ {⊕, ª}. If an explicit authorization A

of y

∈ H

propagates to y

∈ H, then A

is converted to an implicit authorization A

by the

following processes: if A

.ruling = +, then A

.ruling = ⊕; if A

.ruling = −,

then A

.ruling = ª; A

.precedence = A

.precedence.

Here is an example of assigning explicit authorizations, assume Γ

= {γ

, γ

};

= (..., γ

, ..., read, +, 1), γ

= (..., γ

, ..., read, −, 2), where γ

= γ

y ∈ H

; then A

= (+, 1), A

= (−, 2). Two authorizations A

, A

are inequable

if either A

.ruling 6= A

.ruling or A

.precedence 6= A

.precedence holds. When

an element of a hierarchy has more than one inequable authorizations, conﬂicts arise.

Our system provides methods of conﬂicts resolution, called authorization precedence

policy. In our system, conﬂicts can be solved either manually or automatically. For a

hierarchy H

= (Y

, ≤

), the System Security Ofﬁcer (SSO) deﬁnes a manual resolution

set M R

⊆ Y

. If an element y ∈ MR

has authorization conﬂicts, we assign y with

139

the authorization (¯, ). In this case, the decision of the access request α that causes the

conﬂicts will be pending until the conﬂicts are manually solved by SSO. If an element

y ∈ Y

\ MR

has authorization conﬂicts, these conﬂicts are solved automatically by

the following rules.

• ¯ authorizations are with the highest precedence; ⊗ authorizations are with the

lowest precedence. There are no maximum and minimum integers in Z, hence the

precedence entries of these two types of authorizations are absent. An authorization

with higher precedence overrides authorizations with lower precedences.

•

If the precedences are the same, denies-take-precedence will apply. The priority

order is: −, ª, +, ⊕. An authorization with higher priority order overrides autho-

rizations with lower priority orders.

Our authorization precedence policy is very ﬂexible. Authorization pending gives

SSO opportunities to review authorization conﬂicts. By doing that, SSO may ﬁnd bugs

of Γ and give user better response. After we perform all authorization derivations and

conﬂicts resolutions on H

, H

’s ﬁnal authorization state is obtained, where ∀y ∈ H

y has a ﬁnal authorization F A

that is not conﬂicting. The result of the sub-validation

of α

is F A

.ruling. The decision of α is processed as follows.

• If ∀F A

.ruling = + (or ⊕) where n ≥ i ≥ 1, then α is approved.

•

If ∃F A

.ruling = − (or ª or ⊗), then α is denied.

•

If α is not denied and ∃F A

.ruling = ¯, then α is pending.

4 Hierarchy Semantics of GRBAC and E-P3P

Hierarchy semantics deﬁnes rules of authorization propagation. In this section, the hi-

erarchy semantics of GRBAC and E-P3P is depicted.

4.1 Hierarchy Semantics of GRBAC

The hierarchy semantics in GRBAC [1] is deﬁned by permission inheritance. There are

three types of permission inheritances: standard, strict and lenient. Suppose we have

an access request α = (α

, α

T H

, α

), where α

= y

∈ GH, denoted as

GH.y

, α

T H

= T H.y

and α

= EH.y

. Here we utilize the validation of GH.y

to illustrate the semantics of the three types of permission inheritances.

• Standard permission inheritance:

If ∃y

∈ Aset

GH.y

∪{GH.y

} such that F A

.ruling = + and ¬∃y

∈ Aset

GH.y

∪

{GH.y

} such that F A

.ruling = −, then GH.y

is authorized for α

. Other-

wise, it is not authorized for α

• Lenient permission inheritance:

If ∃y

∈ Aset

GH.y

∪ {GH.y

} such that F A

.ruling = +, then GH.y

authorized for α

. Otherwise, it is not authorized for α

•

Strict permission inheritance:

If ∀y

∈ Aset

GH.y

∪ {GH.y

} such that F A

.ruling = +, then GH.y

authorized for α

. Otherwise, it is not authorized for α

140

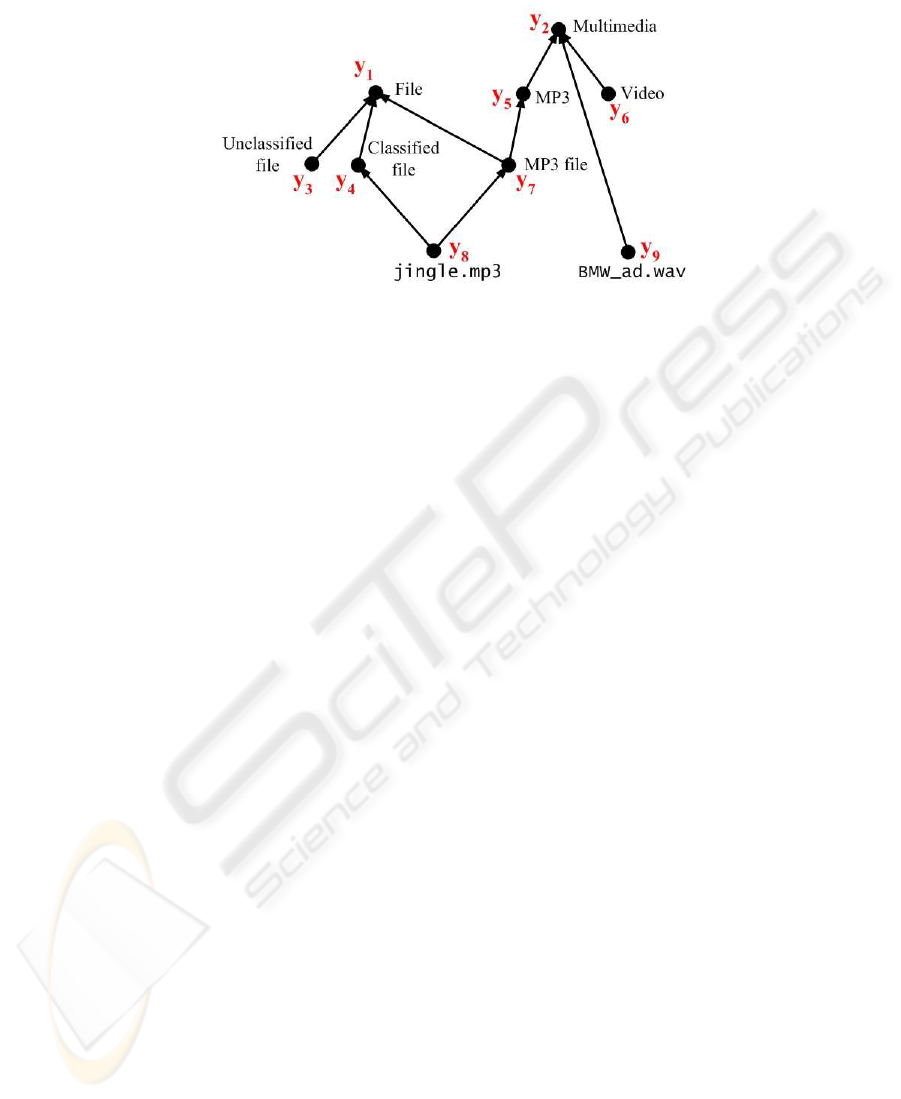
Fig.1. Example object hierarchy T H

An example below illustrates the hierarchy semantics of GRBAC. Consider the

object hierarchy T H shown in ﬁgure 1; there are 9 elements in T H, among which

jingle.mp3 (y

) is a primitive category that is a child of classiﬁed ﬁle (y

) and MP3

ﬁle (y

). Now there is an access request α from user u (we assume u is y

in GH) to

read jingle.mp3 (T H.y

) under environment e (we assume e is y

in EH), i.e. α =

(GH.y

, T H.y

, EH.y

, read ). The policy rule set Γ = {γ

, γ

}; γ

= (GH.y

, T H.y

EH.y

, read, +), γ

= (GH.y

, T H.y

, EH.y

, read, +). Obviously, the matching

rule set Γ

= Γ . According to GRBAC hierarchy semantics, we can derive that u can

read jingle.mp3 if standard or lenient permission inheritance is applied; u cannot read

it if strict permission inheritance is applied.

The original intention of strict permission inheritance is to restrict accesses to the

elements in the category of sensitive/vulnerable categories deﬁned by SSO. GRBAC’s

strict permission inheritance is trying to fulﬁll this intention. However this deﬁnition

is too strict to be practical. In the example above, user u is explicitly authorized to

read both classiﬁed ﬁle and MP3 ﬁle and there is no policy rule disallow these accesses

(as shown in the example Γ above). In this case, even if we are very strict, user u

should have read access to jingle.mp3, which is a child of classiﬁed ﬁle and MP3 ﬁle.

GRBAC will deny this access because GRBAC’s strict permission inheritance requires

the requested element and all its ancestors to be explicitly authorized for the access;

obviously this is too strict. If a system deploys this strict permission inheritance, few

access requests can be granted.

4.2 Hierarchy Semantics of E-P3P

In E-P3P, an access request α is processed in the following two steps [2]. The ﬁrst

step creates a set of preliminary authorization rules P A; P A is a rule set deﬁned as the

union of Γ and DΓ , where DΓ contains all rules derived from Γ by using the hierarchy

semantics deﬁned in this system. The second step processes access request α according

to P A.

141

The hierarchy semantics of E-P3P is deﬁned as follows [2]:

• Down-inheritance: For each rule (i, t, p, u, r, a,

c) ∈ P A, for every (t

, p

, u

)

such that t

≤

t, p

≤

p, and u

≤

u, a tuple (i, t

, p

, u

, r, a,

c) is added to

P A.

•

Up-inheritance of deny (negative authorization): For each rule (i, t, p, u, −, a,

c) ∈

P A, for every (t

, p

, u

) such that t ≤

, p ≤

, and u ≤

, a tuple

(i, t

, p

, u

−, a,

c) is added to P A.

In this system, if contradicting policy rules coexist, denies-take-precedence will be

applied to remove contradicting policy rules with lower precedences from P A.

We can identify two problems existing in this system. The ﬁrst problem is that the

concept of permission inheritance is omitted. As a consequence, the system is not ﬂex-

ible in practice. For example, it provides no mechanism for enforcing strict permission

inheritance. The second problem is that the deﬁnition of up-inheritance of deny is rea-

sonless. The ﬁrst problem is apparent; here we will give an example that reveals the sec-

ond problem. Following the semantics of

up-inheritance of deny

, some reasonable re-

quests from users are denied. Let us consider the following scenario. There is a primitive

category BMW

ad.wav (T H.y

in ﬁgure 1) in the category of multimedia (T H.y

in ﬁg-

ure 1), besides we assume that GH.y

is user u and P H.y

is a purpose. There are two

policy rules in Γ , i.e. Γ = {γ

, γ

}; γ

= (1, T H.y

, P H.y

, GH.y

, −, read, null, null),

= (1, T H.y

, P H.y

, GH.y

, +, read, null, null). Now there is an access request

from user u: α = (T H.y

, P H.y

, GH.y

, read, null, null); i.e. user u requests to

read BMW

ad.wav for the purpose of P H.y

with no speciﬁed condition and obligation.

Because T H.y

≤

T H.y

(see ﬁgure 1), P H.y

≤

P H.y

and GH.y

≤

GH .y

following up-inheritance of deny, there will be a policy rule γ

derived from γ

: γ

(1, T H.y

, P H.y

, GH.y

, −, read, null, nul l), that is user u is not allowed to read

multimedia for the purpose of P H.y

. Then P A = Γ ∪ {γ

}, i.e. P A = {γ

, γ

}

(here we skip other derived rules). The two policy rules γ

and γ

are contradicting

policy rules. Because of denies-take-precedence, the rule γ

will be removed from P A,

now P A = {γ

, γ

}. The system will validate α according to P A = {γ

, γ

}, hence

according to γ

, user u’s request α is denied.

5 Solution

This section presents the hierarchy semantics deﬁned in our generalized PSS. The

semantics described below eliminates the problems mentioned in section 4 and extends

the hierarchy semantics of GRBAC and E-P3P.

5.1 Hierarchy Semantics

Our interpretation of the concept of hierarchy is such that the relationship between a

descendant element and its ancestor element is in the category of. The common ratio-

nale is that when an authorization is applied on an ancestor element (superior category),

this authorization may also be applied to its descendant elements (inferior categories)

142

implicitly. As a consequence, authorizations propagate downwards (¯ and ⊗ authoriza-

tions do not propagate; the term authorization in this sub-section denotes authorizations

other than ¯ and ⊗ authorizations). We only consider authorization propagations be-

tween parents and children here; any complex authorization propagation is an aggrega-

tion of such simple propagations. In a hierarchy, two different types of elements must

be clearly distinguished. Pure element is an element that has only one parent; hybrid

element is an element that has more than one parents. Based on these two types of ele-

ments, two different situations of down-propagation of authorizations can be identiﬁed.

• If a child is a pure element, all authorizations of its parent propagate down.

• If a child is a hybrid element, the hierarchy semantics is complicated. There are

many options that represent different strictness of authorization propagation. These

options are listed as follows.

(a) Strict down-propagation: SSO deﬁnes a combination of elements called Strict

Combination (SC). For a child y, if ∃y

∈ P set

such that y

∈ SC, then

the authorization propagation from y’s parents to y will follow the semantics

of strict down-propagation. We deﬁne a set SC

= {y

: y

∈ P set

and

∈ SC}. The semantics of strict down-propagation is as follows.

All (implicit) negative authorizations of elements in P set

\SC

propagate

down to y; all other authorizations of elements in P set

propagate down

to y iff ∀y

∈ SC

such that F A

.ruling = + (or ⊕).

(b)

Lenient down-propagation: SSO deﬁnes a combination of elements called Le-

nient Combination (LC). For a child y, if ∃y

∈ P set

such that y

∈ LC

and ¬∃y

∈ P set

such that y

∈ SC (for security concern, strict down-

propagation overrides lenient down-propagation), then the authorization propa-

gation from y’s parents to y will follow the semantics of lenient down-propagation.

We deﬁne a set LC

= {y

: y

∈ P set

and y

∈ LC}. The semantics of

lenient down-propagation is as follows.

If ¬∃y

∈ LC

such that F A

.ruling = + (or ⊕), all authorizations of

elements in P set

propagate down to y.

ii. If ∃y

∈ LC

such that F A

.ruling = + (or ⊕), all authorizations of

elements in {y

: y

∈ P set

and F A

.ruling = + (or ⊕)} propagate

down to y.

(c)

Standard down-propagation: For a child y, if ¬∃y

∈ P set

such that y

∈ LC

and ¬∃y

∈ P set

such that y

∈ SC, then the authorization propagation

from y’s parents to y will follow the semantics of standard down-propagation.

The semantics of standard down-propagation is as follows.

i. All authorizations of y’s parents propagate down to y.

The semantics described above generalizes the hierarchy semantics in GRBAC and

E-P3P.The strict permission inheritance deﬁned in GRBAC (section 4.1) is a special

case of our deﬁnition of strict down-propagation where ∀y

∈ P set

, y

∈ SC. The

lenient permission inheritance deﬁned in GRBAC (section 4.1) is a special case of our

deﬁnition of lenient down-propagation where ∀y

∈ P set

, y

∈ LC. The proposed

hierarchy semantics also eliminates the questionable semantics in GRBAC and E-P3P. If

our strict down-propagation is applied in the examples shown in section 4.1 and section

4.2, the reasonable access requests will be approved. The semantics of up-inheritance

of deny (section 4.2) is incorrect; hence in our hierarchy semantics it is not included.

143

5.2 Scenarios of the Use of Hierarchy Semantics

This section shows some examples of using the hierarchy semantics deﬁned in this

paper. In these examples, we assume authorization conﬂicts are resolved automatically.

Due to limited space, the examples of down-propagation to a pure element and standard

down-propagation are not included in this paper.

Fig.2. Example strict down-propagation of object hierarchy

Figure 2 shows two examples of strict down-propagation. In the ﬁrst example, a

primitive category jingle.mp3 (y

) enters two categories: classiﬁed ﬁle (y

) and MP3

ﬁle (y

). In this case, SSO wants to be strict to accesses to elements entering category

. SSO deﬁnes SC = {y

}. Because F A

.ruling = +, F A

propagates down

to y

: A

= (⊕, 1). A

is the only authorization that y

has, hence F A

= A

In the second example, a primitive category Jack

s credit history (y

) enters two

categories: sensitive information (y

) and private information (y

). SSO wants to be

strict to accesses to elements entering y

or y

. SSO deﬁnes SC = {y

, y

}. Because

F A

.ruling = + and F A

.ruling = +, F A

and F A

propagate down to y

After conﬂict resolution, F A

= (⊕, 2).

Fig.3. Example lenient down-propagation of object hierarchy

An example of lenient down-propagation is shown in ﬁgure 3. SSO wants to be

lenient to those who are allowed to access emergency information (y

), because emer-

gency information is often related to vital event. SSO deﬁnes LC = {y

} and we

144

assume SC = ∅. Then even if the other parent y

of patient allergic history (y

) is

denied access, y

is still accessible to those who are allowed to access y

6 Conclusion and Future Work

PSSs are capable of expressing and enforcing rich data protection policies. GRBAC

and E-P3P are representatives of such systems. In GRBAC and E-P3P, hierarchy is an

important and widely used concept. Being an inseparable part of hierarchy, hierarchy

semantics deﬁnes rules of authorization propagation. In this paper, we have proposed

a generalized PSS that covers GRBAC and E-P3P. Based on this generalized PSS,

we analyze the hierarchy semantics used in GRBAC and E-P3P. We point out errors

and limitations of GRBAC and E-P3P hierarchy semantics. Finally, we present new

hierarchy semantics to address the problems discovered.

In the future, the following research work interests us:

• ﬁnding more useful hierarchy semantics.

• investigating efﬁcient access request processing mechanisms.

•

reviewing other related work such as access control for XML document etc.

References

1. Moyer, M.J., Ahamad, M.: Generalized role-based access control. In: Proceedings of 21st

International Conference on Distributed Computing Systems. (2001) 391–398

2. Ashley, P., Hada, S., Karjoth, G., Schunter, M.: E-P3P privacy policies and privacy authoriza-

tion. In: Proceeding of the ACM workshop on Privacy in the Electronic Society, ACM Press

(2002) 103–109

Ferraiolo, D.F., Sandhu, R., Gavrila, S., Kuhn, D.R., Chandramouli, R.: Proposed NIST stan-

dard for role-based access control. ACM Transactions on Information and System Security

(TISSEC) 4 (2001) 224–274

Moffett, J.D.: Control principles and role hierarchies. In: Proceedings of the third ACM

workshop on Role-based access control, ACM Press (1998) 63–69

5. Sandhu, R.: Role activation hierarchies. In: Proceedings of the third ACM workshop on

Role-based access control, ACM Press (1998) 33–40

6. Joshi, J.B.D., Bertino, E., Ghafoor, A.: Hybrid role hierarchy for generalized temporal role

based access control model. In: Proceedings of 26th Annual International Computer Software

and Applications Conference. (2002) 951–956

Moffett, J.D., Lupu, E.C.: The uses of role hierarchies in access control. In: Proceedings of

the fourth ACM workshop on Role-based access control, ACM Press (1999) 153–160

8. Jajodia, S., Samarati, P., Sapino, M.L., Subrahmanian, V.S.: Flexible support for multiple

access control policies. ACM Transactions on Database Systems (TODS) 26 (2001) 214–260

145