Performance Guarantee in a New Hybrid Push-Pull Scheduling

Algorithm

Navrati Saxena

and Cristina M. Pinotti

Dept. of Informatics and Telecom., University of Trento, Povo, Trento, Itay,

Dept. of Mathematics and Informatics,

University of Perugia, Perugia, Italy

Abstract. The rapid growth of web services has already given birth to a set of

data dissemination applications. Efﬁcient scheduling techniques are necessary to

endow such applications with advanced data processing capability. In this paper

we have effectively combined broadcasting of very popular (push) data and dis-

semination of less popular (pull) data to develop a new hybrid scheduling scheme.

The separation between the push and the pull data is called cut-off point. The

clients send their request to the server, which ignores the request for the push

items but queues the requests for the pull items. At every instance of time, the

item to be broadcast is designated by applying a pure-push scheduling. On the

other hand, the item to be pulled is the one stored in the pull-queue having the

highest number of pending requests. Fixed a value for the cut-off point, an ana-

lytic model, validated by simulation, evaluates the average system performance.

On the top of that, the major novelty of our system lies in its capability of offer-

ing a performance guarantee to the clients. For each request, the client speciﬁes,

along with the data item requested, the maximum interval of time it can afford

to wait before its request will be served. Based on this particular access-time and

on the analytic model, our hybrid system computes the cut-off point to fulﬁll the

speciﬁc need of the client. The system offers a great ﬂexibility for clients. It im-

proves signiﬁcantly upon a pure push system and some existing hybrid systems

in terms of average waiting time spent by a client.

1 Introduction

Over the past few years, the overwhelming growth of web services has resulted in the

emergence of applications capable of storing and processing a huge set of information.

The prime objective of such data dissemination applications lies in delivering the data to

a very large population of clients with minimum delay. Broadly, all data dissemination

applications have two ﬂavors: in a push-based system the clients continuously monitor

a broadcast process from the server and obtain the data items they require, without

making any requests; on the contrary, in a pull-based system, the clients initiate the

data transfer by sending requests on demand, and the server then makes a schedule to

satisfy these requests. Both push- and pull-based scheduling have their own advantages

and disadvantages. However, neither push nor pull based scheduling alone can achieve

Saxena N. and M. Pinotti C. (2004).

Performance Guarantee in a New Hybrid Push-Pull Scheduling Algorithm.

In Proceedings of the 3rd International Workshop on Wireless Information Systems, pages 50-62

DOI: 10.5220/0002674500500062

 SciTePress

the optimal performance [3], [9]. A better performance could only be achieved when

the two scheduling approaches are combined in an efﬁcient manner.

In this paper, a new, hybrid scheduling is proposed that effectively combines broad-

casting of more popular (push) data and dissemination upon-request for less popular

(pull) data. The clients send their requests to the server, which queues them up for the

pull items. The server continuously broadcasts one push item and disseminates one

pull item. At any instance of time, the item to be broadcast is selected by applying a

pure-push scheduling, while the item to be pulled is the one in the pull-queue having

the maximum number of requests. The cut-off point, that is the separation between the

push and the pull items, is determined in such a way that the clients are served before

the deadline speciﬁed at the time of the request. In other words, the major novelty of

our system lies in its capability of offering a performance guarantee to the clients.

Organization of the paper: The rest of the paper is organized as follows: Sec-

tion 2 reviews related works and subsequently highlights the motivations behind using

our new hybrid algorithm. Section 3 presents our basic algorithm and shows by a

suitable queueing model how to evaluate the system performance, that is the average

waiting time expected in the system, when the value K of the cut-off point is known.

Subsequently, simulation results of the system behavior are discussed brieﬂy. Then, in

Section 4, the complete version of our new algorithm with performance guaranteed is

discussed. Finally, Section 5 concludes the paper by summarizing our work and offers

future directions of research.

2 Related Work and Motivations

As discussed earlier, scheduling algorithms can be broadly classiﬁed into push and pull

based techniques. Given the wide variety of such push and pull based techniques we

only highlight the major schemes here. The optimal expected access time is achieved

when items are equally spaced [12]. The concept of fair channel utilization [6] and ef-

ﬁciency of Packet Fair Scheduling [10], [11] is also investigated. In order to get rid of

ﬁxed access frequencies and number of broadcast channels [14], different heuristics are

also proposed in [15] to solve the NP-complete problem of dynamic broadcast chan-

nels. On the other hand, many preemptive and non-preemptive pull-based algorithms

like First Come First Served (FCFS), Most Requests First (MRF) [13] and R × W

algorithm [4] exist in literature. While MRF provides optimal waiting time for popu-

lar set of items, it suffers from un-fairness. FCFS on the other hand is fair, but suffers

from sub-optimality and convoy effect. A combination of these two [4] often provides

an acceptable solution.

Hybrid approaches, that use the ﬂavors of both push-based and the pull-based schedul-

ing algorithms in one system, appears to be more attractive. In [3], the server pushes all

the data items according to some push-based scheduling, but simultaneously the clients

are provided with a limited back channel capacity to make requests for the items. A

model for assigning the bandwidth to the push- and pull-scheduling in an adaptive way

is proposed in [16]. A hybrid approach is also discussed in [9], which divides the data

items in disjoint push and pull sets, according to their degree of access probability. The

server broadcasts the push items, pre-computed by the Packet Fair Queuing scheduling,

and sends the pull item based on FCFS scheduling discipline, in a reciprocal way. In-

deed, let the push-set consist of the data items numbered from 1 up to K (cut-off point),

and let the remaining items from K + 1 up to D form the pull set. Hence, the average

expected waiting time for the hybrid scheduling is deﬁned as:

exp−hyb

= T

exp−acc

+ T

exp−res

i=1

acc,i

i=K+1

res,i

where: T

exp−acc

is the expected access time for the push-set, T

exp−res

is the expected

response time for the pull-set, P

is the access probability of item i. As the push-set

becomes smaller, the T

exp−acc

becomes shorter, but the pull-set becomes larger, leading

to a longer T

exp−res

. The size of the pull-set might also increase the average access time

acc,i

, for every push item. After having found the minimum number B, called build-

up point, of items to be pushed so that the length of the pull queue in the system is in

average bounded by a constant, [9] chooses, as the cut-off point, the value K such that

K ≥ B and K minimizes the average expected waiting time for the hybrid system.

However, when either the system has a high load, i.e. a high number of requests for

unit of time, and/or all items have almost the same degree of probability, the distinction

between the high and low demand items becomes vague, artiﬁcial, hence the value of

build-up point B increases, ﬁnally leading to the maximum number D of items in the

system. Thus, in those cases, the solution proposed in [9] almost always boils down

to a pure push-based system. This motivates us to develop a more efﬁcient algorithm

capable of improving the access time even in high load with items having same degree

of probability.

Our proposed solution partitions the data items in the push-set and the pull-set, but

it chooses the value of the cut-off point K between those two sets independent of the

build-up point. After each single broadcast, we do not ﬂush out the pull-queue as in

[9]. In contrast, we just pull one single item: the item, which has the largest number of

pending requests. Note that simultaneously with every push and pull, N more access

/ requests arrive to the server, thus the pull-queue grows up drastically at the begin-

ning. In particular, if the pull-set consists of the items from K + 1 up to D, at most

N ×

j=K+1

requests can be inserted in the pull-queue at every instance of time,

out of which, only one, the pull item that has accumulated the largest number of re-

quests, is extracted from the queue to be pulled. However the number of distinct items

in pull-queue cannot grow uncontrolled as it will be shown by the analytic model in the

next section. Once that the analytic model has been devised, we take advantage from

it to make our system more ﬂexible. Indeed, since by the analytic model the system

performance is already known with a good precision, it is possible to decide in advance

if the value of K currently in use at the server will satisfy the client request on time. If

not, K is updated in a suitable way again looking at the system performance analysis.

3 Basic Hybrid Algorithm: Performance Modelling, Simulation

Framework

The basic hybrid algorithm assumes that the value K of the cut-off point is given and

that the client makes a data request without any deadline. Then, the items from 1 to

K are pushed according to Packet Fair Scheduling algorithm and the remaining items

from K + 1 to D are pulled according to Most Request First (MRF) algorithm. The

server listens to all the requests of the clients and manages the pull-queue. The pull-

queue, implemented by a max-heap, keeps in its root, at any instant of time, the item

with the highest number of pending requests. For any request i, if i is larger than the

current cut-off point K, i.e. i > K, it is inserted in the pull-queue, the number of the

pending requests for i increased by one, and the heap information updates accordingly.

Vice versa, if i is smaller than or equal to K, i.e., i ≤ K, the server simply drops the

request because that item will be broadcast by the push-scheduling. The scheduling is

derived as explained in Figure 1, where the details for obtaining the push scheduling

are omitted. The interested reader can ﬁnd them, for example, in [7]. To retrieve a data

item, a client performs the actions as illustrated in Figure 2. Note that the behavior of

client is independent of the fact that the requested item belongs to the push-set or to the

pull-set.

Procedure HYBRID SCHEDULING;

while (true) do

begin

obtain an item from the push scheduling;

broadcast this item;

if the pull-queue (is not empty) then

extract the most requested item;

clear the requests pending for it;

pull this item;

end-if

end;

Fig. 1. Hybrid Scheduling at the Server

In the remaining of this section, we investigate into the performance evaluation of

our basic hybrid scheduling system by developing suitable analytical models. Subse-

quently, we also validate this performance analysis by developing a simulation frame-

work and performing simulation experiments. Before going into the details of analytical

underpinnings, we explicitly state the underlying assumptions in our framework.

1. The arrival rate in the entire system is assumed to obey Poisson distribution with

mean λ

2. The service times of both the push and pull systems are exponentially distributed

with mean µ

and µ

, respectively.

3. The server pushes K items and clients pull the rest (D − K) items. Thus, the total

probability of items in push-set and pull-set are respectively given by

i=1

and

i=K+1

= (1 −

i=1

), where P

denotes the access probability of item

Procedure CLIENT-REQUEST (i):

/* i : client’s required item */

begin

send to the server the request

for item i;

repeat

wait;

until (listen i on channel)

end

Fig. 2. Algorithm at the Client Side

i. We have assumed that the access probabilities P

follow the Zipf’s distribution

with access skew-coefﬁcient θ, such that, P

(1/i)

j=1

(1/j)

0, 0 1, 0

2, 0

i, 0

c, 0

c, 1i, 1

2, 1

1, 1

λ λ

µ µ µ

2 2

1 1

Fig. 3. Performance Modelling of Hybrid System

Figure 3 illustrates the underlying birth and death process of our system, where the

arrival rate in the pull-system is given by λ = (1−

i=1

)λ

. Any state of the overall

system is represented by the tuple (i, j), where i represents the number of items in the

pull-system. On the other hand, j is a binary variable, with j = 0 (or 1) respectively

representing whether the push-system (or pull-system) is currently being served by the

server. Naturally, both the arrival of the data items and their service are responsible

for the dynamics associated with the state transitions in the system. One major goal of

this performance analysis is to capture this system dynamics. This will lead to get an

expected, overall estimate of the system performance. We now enumerate these system

dynamics resulting from arrival and service of data items.

1. The arrival of a data item in the pull-system, results in the transition from state

(i, j) to state (i + 1, j), ∀i, such that 0 ≤ i < ∞ and ∀j ∈ [0, 1].

2. The service results in two different actions. Since, the push system is governed by

Packet Fair Queuein Sgcheduling, the service of an item in the push-queue results

in transition of the system from state (i, j = 0) to state (i, j = 1), ∀i such that 0 ≤

i < ∞. On the other hand, the service of an item in the pull results in transition of

the system from state (i, j = 1) to the state (i−1, j = 0), ∀i, such that 1 ≤ i < ∞.

3. The state of the system at (i = 0, j = 0) represents that the pull-queue is empty

and any subsequent service of the elements of push system leaves the system in the

same (0, 0) state.

4. Obviously, the state (i = 0, j = 1) is not valid because the service of an empty

pull-queue is not possible.

As the system reaches the steady-state, the total ﬂow needs to be conserved. The

overall behavior of the system for both push (upper chain) and pull part (lower chain)

can now be estimated from Chapman-Kolmogrov’s general equation [8]. The steady-

state equations representing the push and pull parts of the system is given below:

p(i, 0)(λ + µ

) = p(i − 1, 0)λ + p(i + 1, 1)µ

(1)

p(i, 1)(λ + µ

) = p(i, 0)µ

+ p(i − 1, 1)λ, (2)

where p(i, j) represents the probability of state (i, j). However, since the state (0, 1)

is invalid and any service from state (0, 0) leaves the system in same state, the initial

condition of the system is represented by:

p(0, 0) λ = p(1, 1) µ

. (3)

The most efﬁcient way to solve Equations (1) and (2) is using z-transforms [8]. ¿From

the deﬁnition of z-transforms, the resulting solutions will be of the form: P

(z) =

∞

i=0

p (i, 0) z

and P

(z) =

∞

i=0

p(i, 1) z

. Hence, dividing both sides of Equa-

tion (1) by µ

, letting ρ =

, f =

, and performing subsequent z-transforms, we

get,

(z) = p (1, 1) + z (ρ + f )[P

(z) − p(0, 0)] − ρ z

(z) (4)

= ρ p (0, 0) + z (ρ + f ) [P

(z) − p (0, 0)] − ρz

(z), [using Equation( 3)]

Now, investigating the system behavior at the initial conditions, we can derive the

following two normalization criteria:

1. The occupancy of pull states is the total trafﬁc of pull queue. This occupancy is

given by:

(1) =

∞

i=1

p(i, 1) = ρ.

2. The occupancy of the push states (upper chain) is similarly estimated by:

(1) =

∞

i=1

p(i, 0) = (1 − ρ).

These above two relations can be used in Equation (4), to obtain the idle probability,

p(0, 0):

(1) = ρ p(0, 0) + (ρ + f) [P

(1) − p(0, 0)] − ρ P

(1) (5)

ρ = f(1 − ρ) − f p(0, 0), (using values of P (1)and P (2))

p(0, 0) = 1 − ρ −

Generalized solution of Equation (4) to obtain all values of probabilities p(i, j)

become very complicated. Thus, the most efﬁcient way is to go for an expected measure

of system performance, such as the average number of elements in the system and

average waiting time. This expected system performance can be conveniently obtained

by differentiating the z-transformed variables, P

(z) and P

(z) and capture their values

at z = 1. Proceeding in this way and differentiating both sides of Equation (4) with

respect to z at z = 1, we get an estimate of the expected number of elements in the

pull-system (E[L

pull

]) as follows:

(z)

z=1

= (ρ + f )

(z)

z=1

+ P

(1) (f − ρ) − p(0, 0) (ρ + f ) − ρ

(z)

z=1

(6)

E[L

pull

] = (ρ + f ) E[L

push

] + (1 − ρ) − (ρ + f )(1 − ρ −

) − ρ E[L

push

]

i=1

1 −

−

λ + µ

¶µ

1 −

−

, (as E[L

push

] =

i=1

) (7)

where E[L

push

] denote the the expected system performance for the push part, and

where, according to the Packet Fair Queueing Scheduling, S

is the space between two

instances of the same data item i deﬁned as S

j=1

√

and

j=1

Once, we have the expected number of items in the pull system from Equation (6),

using Little’s formula [8], we can easily obtain the estimates of average waiting time of

the system (E[W

pull

]), average waiting time of the pull queue (E[W

pull

]) and expected

number of items (E[L

pull

]) in the pull queue as:

E[W

pull

] =

E[L

pull

]

; E[W

pull

] = E[W

pull

] −

; E[L

pull

] = E[L

pull

] −

(8)

In conclusion, the expected access-time (E[T

hyb−acc

]) of our hybrid system is given

by:

E[T

hyb−acc

] =

i=1

+ E[W

pull

] ×

i=k+1

(9)

The expressions provided in Equations ( 6), ( 8) and ( 9) provide an estimate of the

average behavior of our hybrid system when the cut-off assume the value of K.

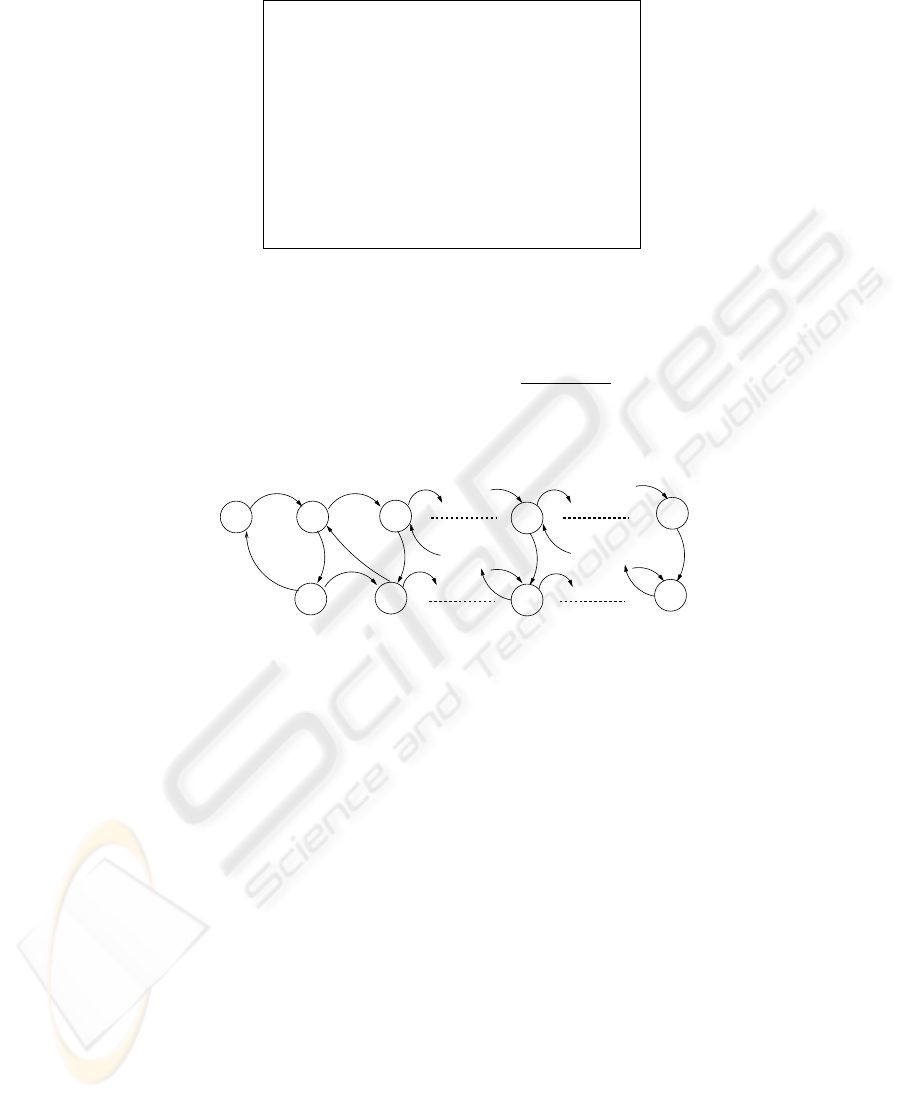
In order to validate the performance analysis, we have compared our analytical

results, obtained from plotting the numerical values of Equation( 9), with the sim-

ulation results assuming D = 100, λ

= 10 (analytic), N = 10 (experimental),

0.50 ≤ θ ≤ 1.30 in correspondance of the value of K which minimize the expected

waiting time in our experiments. The value of µ

and µ

are estimated as µ

i=1

and µ

i=K+1

. Figure 4 demonstrates analytical results closely follow the sim-

ulation results with a deviation of 15%–20%.

Moreover, Figure 5 illustrates, by experimental results, the dynamism of expected

access-time with variation of θ for N = 10 and D = 100. The access-times for different

values of θ have a similar trend and decreases for a cut-off point in the range K ∈

[0, 35]. The curves remains almost ﬂat in the region 35 ≤ K ≤ 50. This points out a

0.5

0.6

0.7

0.8

0.9

1.1

1.2

1.3

Experimental Vs. Analytical results

Access Skew Coefficient (θ)

Expected Access time

Experimental results

Analytical results

Fig. 4. Comparison of Experimental and Analytical Performances

fair and optimal mix of push and pull scheduling. Then the expected access-time start

increasing again.

100

Expected Access Time for N=10

Cut−off Point (K)

Expected Access time

θ = 0.60

θ = 0.80

θ = 1.0

θ = 01.20

Fig. 5. Expected Access Time for N = 10 and D = 100

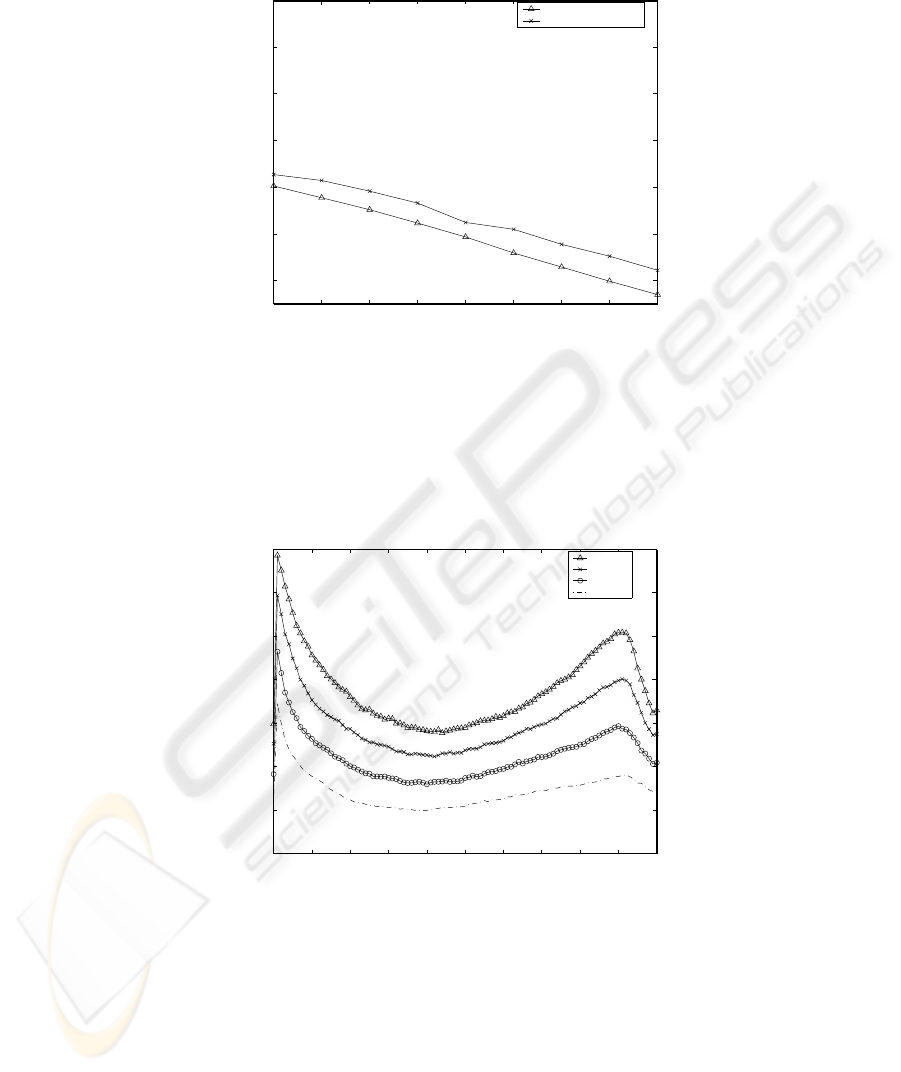
Simulation experiments are also performed to compare our hybrid scheduling scheme

with previous existing scheduling algorithms. We have chosen our previous hybrid

scheduling algorithm [9], and pure-push scheduling algorithm as performance bench-

marks of our new scheduling algorithm. The simulation experiments are evaluated for

D = 100, for N = 10 and N = 20. and for θ varying from 0.50 to 1.30. The results

are reported in Table 1 and 2, respectively for N = 10 and N = 20.

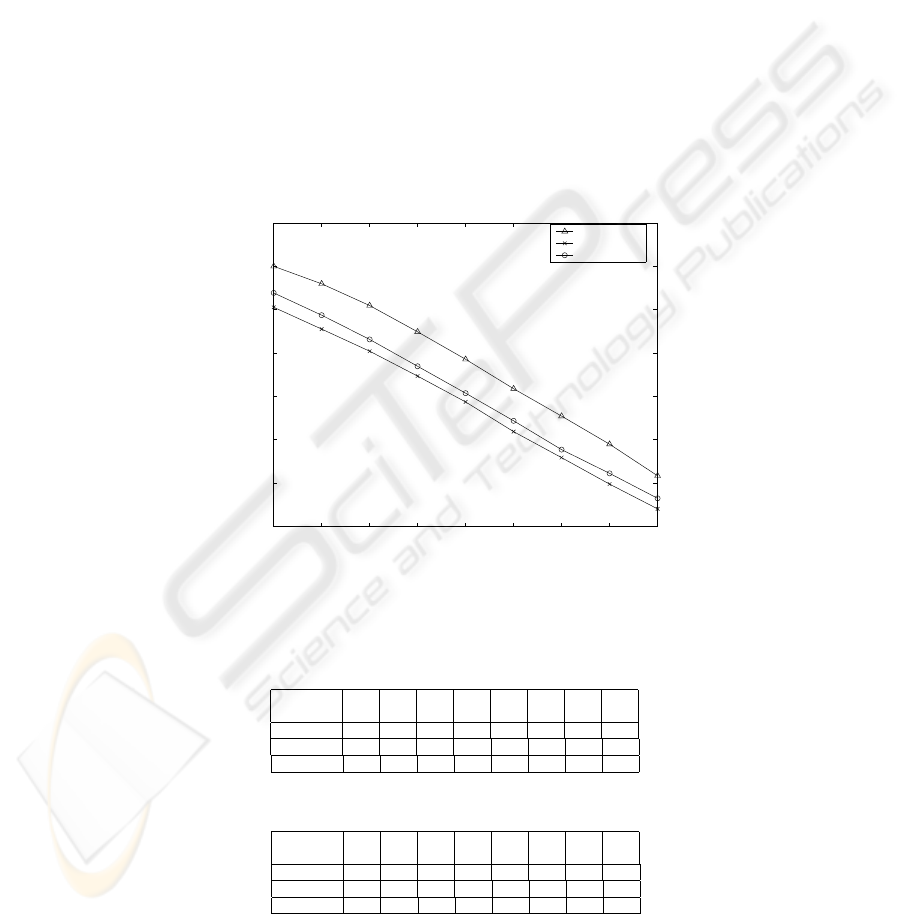
Figures 6 and 7 (B) show the results of performance comparison between our new

algorithm with that of pure-push scheduling and the comparison of the cut-off point

between the new algorithm and [9] when K is selected so that the average waiting

time is minimized. Both of these ﬁgures reveal that our basic new algorithm achieves

an improvement over our existing strategy and over the existing pure-push system. As

earlier discussed, when the system is highly loaded, the scheduling algorithm in [9],

whose cut-off point K must be larger than the build-up point B, almost reduces to the

pure-push scheduling. Contradictory to [9], the new basic hybrid algorithm, even with

very high loaded system, experiments better results than a pure-push based system as

illustrated in Figure 6. Besides, in Figure 7, the values of the cut-off point K for which

the access waiting time of the system is minimal for the basic hybrid algorithm, and for

the hybrid scheduling proposed in [9] are depicted for N = 10 and N = 20.

0.5

0.6

0.7

0.8

0.9

1.1

1.2

1.3

Push Vs. Hybrid, D = 100

Access Skew Coefficient (θ)

Expected Access time

Push

Hybrid−N=10

Hybrid−N=20

Fig. 6. Pure-Push Scheduling Vs New Algorithm

Table 1. T

exp−hyb

for different values of θ (in columns) and different algorithms when N = 10

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

1.30

New 40.30

37.78

35.23

32.36

29.38

25.95

22.95

19.90

17.04

[9] 44.54

42.35

40.01

37.31

34.12

29.93

24.38

20.61

17.04

Push 45.03

43.01

40.50

37.47

34.30

30.90

27.75

24.50

20.86

Table 2. T

exp−hyb

for different values of θ (in columns) and different algorithms when N = 20

0.50

0.60

0.70

0.80

0.90

1.00

1.10

1.20

1.30

New 41.96

39.39

36.59

33.49

30.39

27.20

23.88

21.14

18.26

[9] 44.44

42.45

40.10

37.39

33.78

30.69

27.54

23.23

19.49

Push 44.70

42.61

40.30

37.65

34.12

30.78

27.71

23.94

21.07

0.5

0.6

0.7

0.8

0.9

1.1

1.2

1.3

100

110

120

Cut Off Point with N = 10 and 20

Access Skew Coefficient (θ)

Cut of ponit (K)

New, N=10

[9], N = 10

New, N = 20

[9], N = 20

Fig. 7. Cut-Off Point when N = 10, 20.

4 New Hybrid Scheduling Algorithm

While the performance evaluation of our new basic hybrid scheduling algorithm has

already pointed out its signiﬁcant gains in both response time and minimizing the

value of the cut-off point when compared to existing algorithms and pure push-based

scheduling, we now proceed to mention the complete version of our new algorithm

with performance guaranteed quality that our new scheduling scheme is capable to of-

fer. Such performance guarantee is required to deliver, for example, the wireless voice

and data packets within a precise time-frame of service, thereby ensuring a certain level

of quality-of-service (QoS).

Essentially for all D possible values of the cut-off point, the server computes the

expected hybrid waiting time E[T

hyb−access

] using the Equation( 9) in Section 3. From

now on, let E[T

hyb−access

(i)] denote such expected hybrid waiting time when i is the

cut-off point value. These D expected waiting times are stored, one-at-a time along

with the index of the cut-off point that generates it, sequentially in a vector V . That

is, for all 1 ≤ i ≤ D, V[i, 1] = [E[T

hyb−access

(i)] and V[i, 2] = i]. Moreover V is

maintained sorted with respect to the ﬁrst componenet, i.e. the expected hybrid waiting

time. With this structure, the server can extract the ﬁrst element V[0] of this vector in

a single access, which will indicate in correspondence of which value K

of the cut-

off point the minimum expected hybrid waiting time V[0, 1] = E[T

hyb−access

)] is

achieved. The server broadcasts V[0] from time to time, thereby informing the clients

of the best performance it can provide. Moreover, the server continuously broadcasts

the basic hybrid scheduling that corresponds to the cut-off point K in use we discussed

in previous section. On the other side, when a client sends a request for any item j, it

also speciﬁes an expectation ∆(j) of its possible waiting time for item j. Indeed, ∆(j)

reﬂects the nature of the application, and the tolerance of the client. For example, a

client requesting for any real-time video application, will expect a time much lower than

any client requesting data service-speciﬁc applications. Moreover, an impatient client

could ask that its request is served in a time much lower than its moderate counterparts.

In order to accept a client request for item j with expectation ∆(j), the server es-

timates the expected waiting time for j at this current time instant using the values

stored in vector V and the knowledge of the current cut-off point K in use for the

hybrid scheduling algorithm broadcasted by the server. If the expected hybrid waiting

time provided by the system is smaller or equal to the expectation time of the client’s

request, then the certain level of QoS expected by the client is guaranteed. Otherwise,

the server checks whether the item j belongs to its current push set, that is if j ≤ K.

If this is true, it compares the client request deadline with the expected waiting time

guaranteed by the Packed Fair Scheduling Queueing for the push part of the system,

say E[T

P F S

(j)]. Recall that such a value is known and it is proportional to the space

between two instances of j in the Packed Fair Queueing Scheduling [10], and it is

different from the overall expected waiting time of the server although it depends on

the cut-off point in use. Now, if the expectation of the client 2E[T

P F S

(j)] is smaller

than or equal to ∆(j), the request can still be accepted and the performance guarantee.

Note that the E[T

P F S

(j)] is doubled to take in the ﬁgure the fact that the system pulls

one item between two consecutive puhed items. Otherwise, the request can be accepted

only if the cut-off point is updated. Indeed, the server will perform a binary search on

the vector V to look for a cut-off point value whose corresponding expected hybrid

waiting time is the largest value smaller than or equal to ∆(j). Note that such a value

always exists if V[0, 1] ≤ Delta(j). Then, the cut-off point is updated accordingly and

the scheduling re-initialized. Note that the adjustment in push and pull sets results in

some overheads, and in practice, the server may be forced to reject requests to avoid

to pay such an overhead too frequently. Figure 8 provides a pseudo-code for this entire

procedure of performance guarantee.

5 Conclusion

In this paper we have proposed and analyzed the performance guarantee of a new hy-

brid, scheduling algorithm. In Section 3, we have evaluate a basic hybrid algorithm

which separates the items in two sets, one to be pushed and one to be pulled. The sec-

ond contribution of our approach lies in offering to each client the possibility to specify

a deadline, providing him/her the ﬂexibility to choose his/her best suitable access-time.

To react to a request with expectation time, the system may need to recompute the cut-

off point. The overhead of this operation is kept as low as possible. Future work will

be devoted to study the overhead incurred by the system and how to keep it as low as

possible.

Acknowledgment

The authors are thankful to K. Basu and S.K. Das for their helpful discussions.

1. for (i = 1 to D) do

2. compute the average waiting time E[T

hyb−access

(i)];

3. sort all the values of E[T

hyb−access

(1)], . . . , E[T

hyb−access

(D)] and

store them in increasing order in a vector V

4. broadcast to the clients the min{affordable waiting time} V[0];

5. accept the client’s request for any item j with expected

waiting-time ∆(j) ≥ E[T

hyp−access

(K)], where K = current cut-off;

6. if (condition at line 5 is not verified and j ≤ K)

accept the client’s request for any item j with expected

waiting-time ∆(j) ≥ 2E[T

P F S

(j)], where E[T

P F S

(j)] is the

expected waiting time guaranteed by Packet Fair Scheduling;

7. if (both conditions at lines 5 and 6 are not verified) and

(∆(j) is larger than expected waiting time stored in V [0, 1])

8. get the largest value of E[T

hyb−access

(j)] ≤ ∆(j) from V

9. adjust the cut-off point and restart new hybrid scheduling;

10.otherwise reject the request.

while (true)

Fig. 8. Performance Guarantee in Hybrid Scheduling

References

1. S. Acharya, R. Alonso, M. Franklin and S. Zdonik. Braodcast Disks: Data Management for

Asymmetric Communication Environments. In In the proceedings of ACM SIGMOD Conf.,

San Jose, May 1995.

2. S. Acharya, M. Franklin and S. Zdonik. Dissemination-Based Data Delivery using Broadcast

Disks. In IEEE Personal Communications, pages 50–60, Dec 1995.

3. S. Acharya, M. Franklin, and S. Zdonik. Balancing push and pull for data broadcast. In

Proceedings of the ACM SIGMOD Conference, Tuscon, Arizona, pages 183–193, May, 1997.

4. D. Aksoy and M. Franklin. RxW: A scheduling approach for large scale on-demand data

broadcast. In IEEE/ACM Transactions on Networking, Vol. 7, No. 6, Dec, 1999.

5. A. Bar-Noy, J. S. Naor and B. Schieber. Pushing Dependent Data in Clients-Providers-

Servers Systems. In Mobile Networks and Applications, Vol. 9, pages 421-430, 2003.

6. J. C. R. Bennett and H. Zhang. Hierarchical packet fair queueing algorithms In Proceedings

of ACM SIGCOMM, pages 43-56, 1996.

7. J. Gecsei, The architecture of videotex systems Englewood Cliffs, NJ, Prentice-Hall, 1983

8. D. Gross and C. M. Harris, Fundamentals of Queuing Theory John Wiley & Sons Inc.

9. Y. Guo, S. K. Das and M. C. Pinotti. A new Hybrid Broadcast scheduling Algorithm for

Asymmetric Communication Systems: Push and Pull Data based on Optimal Cut-Off Point.

In Mobile Computing and Communications Review (MC2R), Vol. 5, No. 4, 2001.

10. S. Hameed and N. H. Vaidya. Efﬁcient algorithms for scheduling data broadcast In Wireless

Networks, Vol. 5, pages 183-193, 1999.

11. S. Hameed and N. H. Vaidya. Scheduling data broadcast in asymmetric communication

environments In Wireless Networks, Vol. 5, pages 171-182, 1999.

12. R. Jain and J. Werth. Airdisks and airraid: Modeling and scheduling periodic wireless data

broadcast (extended abstract) In DIMACS Technical Report 95-11, Rutgers University, 1995.

13. M. C. Pinotti and N. Saxena. Push less and pull the current highest demaned data item to

decrease the waiting time in asymmetric communication environments. In 4th International

Workshop on Distributed and Mobile Computing, (IWDC), Calcutta, India pages 203–213.

Springer-Verlag 2002; LNCS 2571, Dec 28-31, 2002.

14. W. C. Peng and M. S. Chen. Dynamic generation of data broadcasting programs for a broad-

cast disk array in a mobile computing environment. In Proceedings of the ACM 9th Confer-

ence on Information and Knowledge Management, pages 38-45, Nov. 2000.

15. W. C. Peng, J. L. Huang and M. S. Chen. Dynamic Levelling: Adaptive Data Broadcasting

in a Mobile Computing Environment. In Mobile Networks and Applications, Vol. 8, pages

355-364, 2003.

16. K. Stathatos and N. Roussopoulos and J. S. Baras. Adaptive data broadcast in hybrid net-

works In Proceedings of 23rd International Conference on Very Large Data Bases, Athens,

Greece, pages 326-335, 1997