Towards a Metrics Suite for Conceptual Models of

Datawarehouses

Manuel Serrano

, Coral Calero

, Juan Trujillo

, Sergio Luján

, Mario Piattini

Alarcos Research Group

Escuela Superior de Informática

University of Castilla – La Mancha

Paseo de la Universidad, 4

13071 Ciudad Real

Dept. de Lenguajes y Sistemas Informáticos

Universidad de Alicante

Apto. Correos 99. E-03080

Abstract. Nowadays most organizations have incorporated datawarehouses as

one of their principal assets for the efficient management of information. It is

vital to be able to guarantee the quality of the information that is stored in the

datawarehouses given that they have become the principal tool for strategic

decision making. The quality of the information depends on the quality of its

presentation and the quality of the datawarehouse. The latter includes the

quality of the multidimensional model, at a conceptual, logical, and physical

level. Over recent years we have proposed and validated several metrics for the

evaluation of the complexity of the multidimensional star model (at a logical

level). In this article we present an initial proposal of metrics for the

multidimensional model at a conceptual level and for their theoretical

validation.

Keywords: datawarehouse, metrics, quality, multidimensional modelling

1. Introduction

Datawarehouses have become the most important trends in business information

technology and represent one of the most interesting areas within the database

industry [14] as they provide relevant and precise information enabling the

improvement of strategic decisions [26] and as such the quality of the information that

they contain must be guaranteed [15]. In fact, a lack of quality can have disastrous

consequences from both a technical [13] and organizational point of view: loss of

clients [34], important financial losses [30] or discontent amongst employees [15].

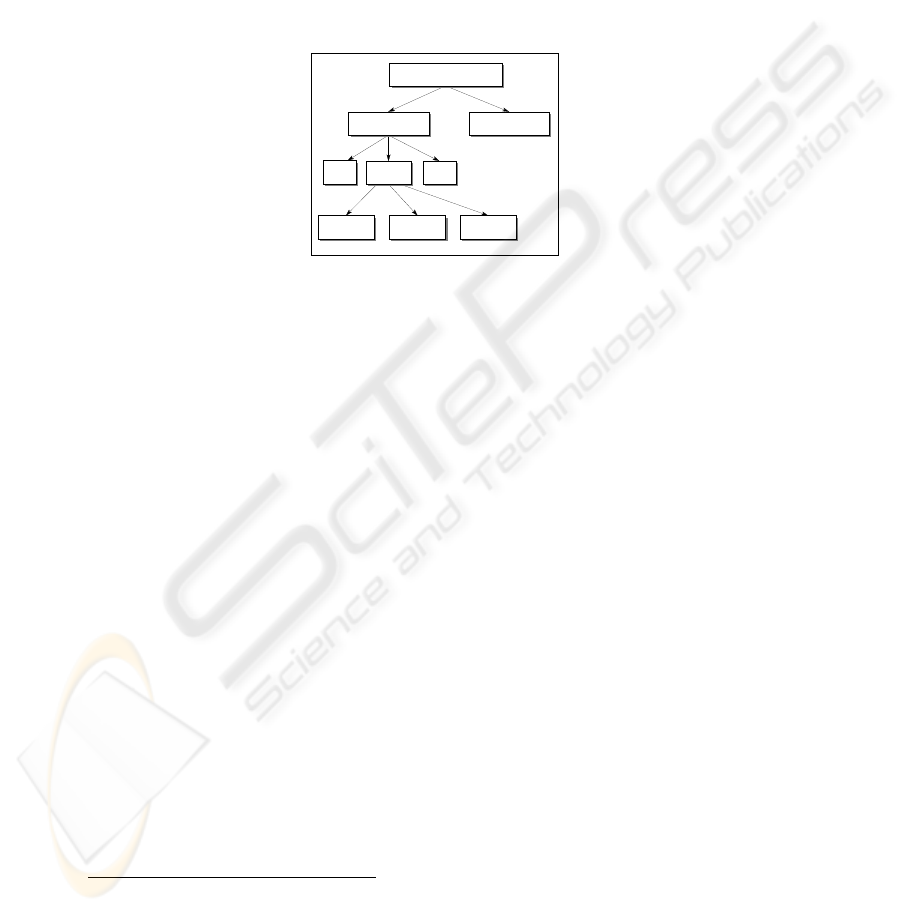
The quality of the information of a datawarehouse is determined by the quality of

the system itself as well as by the quality of the presentation of the data (see figure

1).

Serrano M., Calero C., Trujillo J., Luján S. and Piattini M. (2004).

Towards a Metrics Suite for Conceptual Models of Datawarehouses.

In Proceedings of the 1st International Workshop on Software Audits and Metrics, pages 105-117

DOI: 10.5220/0002675201050117

 SciTePress

Clearly it is important not only that the data of the datawarehouse correctly reflects

the real world, but also that the data is interpreted correctly. As far as the quality of a

datawarehouse is concerned, as with an operational database, three aspects must be

considered: the quality of the relational or multidimensional DBMS (Database

Management System) that supports it, the quality of the data model

(conceptual,

logical and physical) and the quality of the data itself contained in the warehouse.

Fig. 1. Quality of the information and the datawarehouse

In order to guarantee the quality of the DBMS we can use an International Standard

such as ISO/IEC 9126 [25] or one of the comparative studies of existing products.

The quality of the data itself is mainly determined by the processes of extraction,

filtering, cleaning, cleansing, synchronization, aggregation and loading [7], as well as

by the level of maturity of these processes in the organization.

Clearly the quality of the datawarehouse model also strongly influences

information quality. The model can be considered at three levels : conceptual, logical

– for which the use of “star design” has become universal [28] – , and physical –

which depends on each system, and consists of selecting the physical tables, indexes,

data partitions, etc. [8] [22] [26] [29].

At the logical level several recommendations exist in order to create a “good”

dimensional data model [28] [3] [24] and in recent years we have proposed [36] and

validated both theoretically [11] and empirically [37] [38] several metrics that enable

the evaluation of the complexity of star models.

Although conceptual modelling is not usually the object of much attention, there

do currently exist various proposals for representing datawarehouse information from

a conceptual perspective. Some approaches propose a new notation [9] [20] [21]

others use extended E/R models [35] [40] [12] and finally others use the UML class

model [1] [2] [41] [31]. However, it is even more difficult to guarantee the quality of

datawarehouse models, with the exception of the model proposed by Jarke et al [26],

which is described in more depth in [42]. Nevertheless, even this model does not

propose metrics that allow us to replace the intuitive notions of “quality” with regards

We will use the term “model” without distinction to refer to both a modelling technique or

language (eg. The E/R model) and the result (“schema”) of applying this technique to a

specific Universe of Discourse. The difference between the two concepts can be easily

deduced from the context)

INFORMATION QUALITY

DATAWAREHOUSE

QUALITY

PRESENTATION QUALITY

DBMS

QUALITY

DATA MODEL

QUALITY

DATA

QUALITY

LOGICAL MODEL

QUALITY

PHYSICAL

MODEL QUALITY

CONCEPTUAL

MODEL QUALITY

106

to the datawarehouse conceptual model with formal and quantitative measures that

reduce subjectivity and bias in evaluation, and guide the designer in his work.

The final objective of our study is to define a set of metrics to guarantee the quality

of the conceptual models of datawarehouses. In particular, we will focus on the

complexity of the models obtained, which is one of the most important factors in

relation to quality in datawarehouses – along with others such as completion,

minimality and traceability [42] – and which affects comprehensibility, one of the

most important dimensions in data quality [34]

In the next section we summarize the extension of the UML [41] [31] which we

will use as a base for the object – oriented conceptual modelling of the

datawarehouses. In section 3 we present an initial proposal of metrics for the

datawarehouse conceptual model which are described along with an example and

their theoretical validation. Lastly, we draw conclusions and describe future

investigation arising from this present paper.

2. Object – oriented conceptual modelling for datawarehouses

In this section we outline our approach to conceptual modelling based on UML for

the representation of structural properties of multidimensional modelling

This approach has been specified by means of UML profiles

that contains the

necessary stereotypes in order to carry out conceptual modelling successfully [31].

Tables 1 and 2 present in a summarized form the defined stereotypes along with a

brief description and the corresponding icon in order to facilitate their use and

interpretation. These stereotypes are classified as class stereotypes (table 1) and

attribute stereotypes (table 2) as the metrics analyzed in following sections will be

performed based on this classification.

Table 1. Stereotypes of Class

NAME DESCRIPTION ICON

Fact

Classes of this stereotype

represent facts in a MD model

Dimension

Classes of this stereotype

represent dimensions in a MD

model

Base

Classes of this stereotype

represent dimension hierarchy

levels in a MD model

Due to space limitations we will not look at the dynamic properties of multidimensional

modeling in this article.

A profile is a set of improvements that extend an existing UML type of diagram for a different

use. These improvements are specified by means of extendibility mechanisms provided by

UML (stereotypes, properties and restrictions) in order to be able to adapt it to a new method

or model.

107

Table 2. Stereotypes of Attribute

NAME DESCRIPTION ICON

OID

Attributes of this stereotype represent OID

attributes of Fact, Dimension or Base classes in a

MD model

OID

FactAttribute

Attributes of this stereotype represent attributes

of Fact classes in a MD model

Descriptor

Attributes of this stereotype represent descriptor

attributes of Dimension or Base classes in a MD

model

DimensionAttribute

Attributes of this stereotype represent attributes of

Dimension or Base classes in a MD model

In our approach, the structural properties of multidimensional modelling are

represented by means of a class diagram in which the information is organized in

facts and dimensions. Some of the principal characteristics that can be represented in

this model are the relations “many-to-many” between the facts and one specific

dimension, the degenerated dimensions, the multiple classification and alternative

path hierarchies, and the non strict and complete hierarchies.

Facts and dimensions are represented by means of fact classes (Fact stereotype)

and dimension classes (Dimension stereotype) respectively. Fact classes are defined

as compound classes in an aggregation relation of n dimension classes. The minimum

cardinality in the role of the dimension classes is 1 to indicate that all the facts must

always be related to all the dimensions. The relations “many-to-many” between a fact

and a specific dimension are specified by means of the cardinality 1...* in the role of

the corresponding dimension class. A fact is composed of measurements or fact

attributes (stereotype FactAttribute) and it is on these that we wish to focus our

analysis.

By default, all the measures in a class of facts are considered to be additive. The

semi-additive and non-additive measures are specified by means of restrictions.

Furthermore, derived measures can also be represented (by means of the restriction / )

and their rules of derivation are specified in keys around the corresponding class of

facts.Our approach also allows the definition of identifying attributes (stereotype

OID). In this way “degenerated dimensions” can be represented [27], which provide

the facts with other characteristics in addition to the defined measures.

As regards dimensions (stereotype Dimension), each level of a classification

hierarchy is represented by means of a base class (stereotype Base ). An association of

base classes specifies a relation between two levels of a classification hierarchy. The

only prerequisite is that these classes should define a Directed Acyclic Graph (DAG)

from the class of dimension (DAG restriction is defined in the stereotype Dimension)

The DAG structure enables the representation of both multiple and alternative path

hierarchies. Each base class must contain an identifying attribute (stereotype OID)

108

and a descriptive attribute

(stereotype Descriptive) in addition to the additional

attributes that characterize the instances of that class.

Due to the flexibility of UML, we can consider the peculiarities of classification

hierarchies as non-strict hierarchies (an object of an inferior level belongs to more

than one of a superior level) and as complete hierarchies (all the members belong to a

single object of a superior class and that object is composed exclusively of those

objects). These characteristics are specified by means of the cardinality of the roles of

the associations and the restriction completeness respectively. Lastly, the

categorization of dimensions is considered by means of the generalization /

specialization hierarchies belonging to UML.

3. Metrics for Datawarehouses

The definition of metrics must be carried out in a methodological fashion, which

means that a series of steps must be followed in order to ensure the reliability of the

proposed metrics [10] . In this paper we will pay special attention to two of these

steps :

• Definition of metrics. this must be done taking into account the specific

characteristics of the system that we wish to measure, as well as the experience of

the designers of these systems. Furthermore, we should aim to make the metrics

that we define simple and easy to automate [16].

• Theoretical validation. Theoretical validation pursue the goal of knowing if the

metrics actually measure the attribute they pretend to measure and help us to know

where and how to apply the metrics. There are two main tendencies as regards

validation: those frameworks based on axiomatic approaches [43] [6] and those

based on the measurement theory [44] [45] [33]. In this paper we will validate the

metrics following the DISTANCE framework [33].

3.1. Definition of the Metrics

Taking into account the metrics defined for datawarehouses at a logical level [37] and

the metrics defined for UML class diagrams [17] [18] [19] we can propose an initial

set of metrics for the model described in the previous section. When drawing up the

proposal of metrics for datawarehouse models, we must take into account 3 different

levels:

Class scope metrics

These metrics are defined for measuring single classes in a datawarehouse conceptual

model. Table 3 shows the proposed class scope metrics.

The identifying attribute is used in the OLAP tools in order to identify univocally the

instances of one hierarchy level and the descriptive attribute as a label by default in the

analysis of data.

109

Star scope metrics

The following table (see table 4) details the metrics proposed for the star level, one of

the main elements of a datawarehouse, composed of a fact class together with all the

dimensional classes and associated bases.

Diagram scope metrics

Lastly in table 5, we present metrics at diagram level of a complete datawarehouse

which may contain one or more stars.

Table 3. Class scope metrics

Metric Description

NA(C)

Number of attributes FA, D or DA of the class C

NR(C)

Number of relationships (of any type) of the class C

Table 4. Star scope metrics

Metric Description

NDC(S)

Number of dimensional classes of the star S

(equal to the number of aggregation relations)

NBC(S)

Number of base classes of the star S

NC (S)

Total number of classes of the star S. NC(S) = NDC(S) + NBC(S) + 1

RBC(S)

Ratio of base classes. Number of base classes per dimensional class of the star S

NAFC(S)

Number of FA attributes of the fact class of the star S

NADC(S)

Number of D and DA attributes of the dimensional classes of the star S

NABC(S)

Number of D and DA attributes of the base classes of the star S

NA(S)

Total number of FA, D and DA attributes of the star S.

NA(S) = NAFC(S) + NADC (S) + NABC(S)

NH(S)

Number of hierarchy relationships of the star S

DHP(S)

Maximum depth of the hierarchy relationships of the star S.

RSA(S)

Ratio of attributes of the star S. Number of attributes FA divided by the number of D

and DA attributes.

Table 5. Diagram scope metrics

Metric Description

NFC

Number of Fact classes

NDC

Number of dimensional classes

NBC

Number of base classes

Total number of classes. NC = NFC + NDC + NBC

RBC

Ratio of base classes. Number of base classes per dimensional class

NSDC

Number of dimensional classes shared by more than one star

NAFC

Number of FA attributes of the fact classes

NADC

Number of D and DA attributes of the dimensional Tables.

NASDC

Number of D and DA attributes of the shared dimensional classes.

Number of FA, D and DA attributes

Number of hierarchies

DHP

Maximum depth of the hierarchical relationships

RDC

Ratio of dimensional classes. Number of dimensional classes per fact class.

RSA

Ratio of attributes. Number of FA attributes divided by the number of D and DA

attributes.

110

3.2. Example

Figure 2 gives an example of a datawarehouse, whilst tables 6, 7 and 8 summarize the

values for the metrics. As the example has only one star, in table 6 only those values

of the metrics that are different at star and model level are shown.

Sales

OID

ticket_number

qty

price

inventory

Product

OID

product_code

name

color

size

weight

Time

OID

time_code

day

qty

working

day_number

Store

OID

store_code

name

address

telephone

Month

OID

month_code

name

Quarter

OID

quarter_code

description

Semester

OID

semester_code

description

Year

OID

year_code

description

Category

OID

category_code

name

Department

OID

department_code

name

City

OID

city_code

name

population

Country

OID

country_code

name

population

Fig. 2. Example of an Object Oriented datawarehouse conceptual model

Table 6. Class level

metrics values

Table 7. Star level

metrics values

Table 8. Model

level metrics values

CLASS NA NR Metric Value Metric Value

Sales 3 3 NDC(S) 3 NFC 1

Time 4 2 NBC(S) 8 NSDC 0

Product 4 2 NC (S) 12 NASDC 0

Store 3 2 RBC 8/3 RDC 3

Month 1 3 NAFC(S) 3

Quarter 1 2 NADC(S) 11

Semester 1 2 NABC(S) 10

Year 1 2 NA(S) 24

Category 1 2 NH(S) 3

Department 1 1 DHP(S) 3

City 2 2 RSA(S) 3/21

Country 2 1

3.3 Theoretical validation

We have theoretically validated the metrics proposed using the Distance framework

[33]. This framework is based on the measurement theory, and consequently enable

the scale to which a metric belongs to be determined.

111

3.3.1. The Distance framework

The DISTANCE framework provides constructive procedures to model software

attributes and define the corresponding measures [33]. The different procedure steps

are inserted into a process model for software measurement that (i) details for each

task the required inputs, underlying assumptions and expected results, (ii) prescribes

the order of execution, providing for iterative feedback cycles, and (iii) embeds the

measurement procedures into a typical goal-oriented measurement approach such as,

for instance, GQM [4] [5]. The framework is called DISTANCE as it builds upon the

concepts of distance and dissimilarity (i.e., a non-physical or conceptual distance). In

this section we summarise the procedures for attribute definition and measure

construction for ease of reference. This distance-based measure construction process

consists of five steps:

• Find a measurement abstraction.

• Model distances between measurement abstractions

• Quantify distances between measurement abstractions

• Find a reference abstraction.

• Define the software measure.

Further details on the measurement theoretical principles underlying the

DISTANCE framework can be found in [33].

3.3.2. NDC Theoretical Validation

The Number of Dimensional Classes (NDC) measure is defined at the diagram level

as the total number of dimensional classes within a datawarehouse conceptual model.

In the following we will follow each of the steps for measure construction

proposed in the DISTANCE framework. In order to exemplify the process we will use

the models shown in figure 3.

Sales

Time

Product

Store

Sales

Time

Product

DCM A

DCM B

Fig. 3. Two examples of conceptual models of datawarehouse

• Step 1. Find a measurement abstraction. In our case the set of software entities P

is the Universe of datawarehouse conceptual models (UDCM) that is relevant for

some Universe of Discourse (UoD) and p is a Datawarehouse Conceptual Model

(DCM) (i.e. p ∈ UDCM). The attribute of interest attr is the number of

dimensional classes, i.e. a particular aspect of DCM structural complexity. Let

UDC be the Universe of Dimensional Classes relevant to the UoD. The set of

dimensional classes within a DCM, called SDC(DCM) is then a subset of UDC.

All the sets of dimensional classeswithin the DCMs of UDCM are elements of the

112

power set of UDC, denoted by ℘(UDC). As a consequence we can equate the set

of measurement abstractions M to ℘(UDC) and define the abstraction function as:

abs

NDC

: UDCM → ℘(UDC): DCM → SDC(DCM)

This function simply maps a DCM onto its set of dimensional classes.

In our example we have the set of dimensional classes of DCM A and of DCM B:

abs

NDC

(DCM A) = SDC(DCM A) = {Time, Store, Product}

abs

NDC

(DCM B) = SDC(DCM B) = {Time, Product }

• Step 2. Model distances between measurement abstractions. The next step is to

model distances between the elements of M. We need to find a set of elementary

transformation types for the set of measurement abstractions ℘(UDC) such that

any set of dimensional classes can be transformed into any other set of dimensional

classes by means of a finite sequence of elementary transformations. Finding such

a set is quite easy in case of a power set. Since the elements of ℘(UDC) are sets

of dimensional classes, T

must only contain two types of elementary

transformations: one for adding a dimensional class to a set and one for removing a

dimensional class from a set. Given two sets of dimensional classes s

∈ ℘(UDC)

and s

∈ ℘(UDC), s

can always be transformed into s

by removing first all the

dimensional classes from s

that are not in s

, and then adding all the dimensional

classes to s

that are in s

, but were not in the original s

. In the 'worst case

scenario', s

must be transformed into s

via an empty set of attributes. Formally, T

= {t

0-NDC

, t

1-NDC

}, where t

0-NDC

and t

1-NDC

are defined as:

0-NDC

: ℘(UDC) → ℘(UDC): s → s ∪ {a}, with a ∈ UDC

1-NDC

: ℘(UDC) → ℘(UDC): s → s - {a}, with a ∈ UDC

In our example, the distance between abs

NDC

(DCM A) and abs

NDC

(DCM B) can

be modelled by a sequence of elementary transformations that does not remove

any dimensional class from SDC(DCM A) and that adds Store to SDC(DCM A).

This sequence of 1 elementary transformations is sufficient to transform

SDC(DCM A) into SDC(DCM B). Of course, other sequences exist and can be

used to model the distance in sets of dimensional classes between DCM A and

DCM B. But it is obvious that no sequence can contain fewer than 1 elementary

transformation if it is going to be used as a model of this distance. All 'shortest'

sequences of elementary transformations qualify as models of distance.

• Step 3. Quantify distances between measurement abstractions. In this step the

distances in ℘(UDC) that can be modelled by applying sequences of elementary

transformations of the types contained in T

, are quantified. A function δ

NDC

that

quantifies these distances is the metric (in the mathematical sense) that is defined

by the symmetric difference model, i.e. a particular instance of the contrast model

of Tversky [39]. It has been proven in [33] that the symmetric difference model

can always be used to define a metric when the set of measurement abstractions is

a power set.

: ℘(UDC) × ℘(UDC) → ℜ: (s, s') → ⏐s – s'⏐ + ⏐s' – s⏐

This definition is equivalent to stating that the distance between two sets of

dimensional classes, as modelled by a shortest sequence of elementary

transformations between these sets, is measured by the count of elementary

transformations in the sequence. Note that for any element in s but not in s' and for

any element in s' but not in s, an elementary transformation is needed.

113

The symmetric difference model results in a value of 1 for the distance between the

set of dimensional classes of DCM A and DCM B. Formally,

NDC

(abs

NDC

(DCM A),abs

NDC

(DCM B)) =

⏐{Time, Store, Product} - {Time, Product }⏐ +

⏐{Time, Product } - {Time, Store, Product}⏐ = ⏐{Store}⏐ + ⏐{ }⏐= 1

• Step 4. Find a reference abstraction. In our example the obvious reference point

for measurement is the empty set of dimensional classes. It is desirable that an

DCM without dimensional classes will have the lowest possible value for the NDC

measure. So that we define the following function:

ref

NDC

: UDCM → ℘(UDC): DCM → ∅

• Step 5. Define the software measure. In our example, the number of dimensional

classes of a Datawarehouse Conceptual Model DCM ∈ UDCM can be defined as

the distance between its set of attributes SDC(DCM) and the empty set of

dimensional classes ∅, as modelled by any shortest sequence of elementary

transformations between SDC(DCM) and ∅. Hence, the NDC measure can be

defined as a function that returns for any DCM ∈ UDCM the value of the metric

NDC

for the pair of sets SDC(DCM) and ∅:

∀ DCM ∈ UDCM: NDC(DCM) = δ

NDC

(SDC(DCM), ∅)

= ⏐SDC(DCM) - ∅⏐ + ⏐∅ - SDC(DCM)⏐

= ⏐SDC(DCM)⏐

As a consequence, a measure that returns the count of dimensional classes in an

Datawarehouse Concpetual Model qualifies as a number of dimensional classes

measure. It must be noted here that, although this result seems trivial, other

measurement theoretic approaches to software measure definition cannot be used

to guarantee the ratio scale type of the NDC measure. The number of dimensional

classes in a DCM can, for instance, not be described by means of a modified

extensive structure, as advocated in the approach of Zuse [45], which is the best

known way to arrive at ratio scales in software measurement.

3.3.3. Other metrics validation

Due to space constraints we cannot present the measure construction process for the

other proposed metrics for datawarehouse conceptual models. However, the process is

analogous and we have obtained that the metrics proposed are on a ratio scale. That

means that they are theoretically valid software metrics because they are in the ordinal

or in a superior scale, as remarked by Zuse [45], and are therefore perfectly usable.

4. Conclusions and Future Research

Businesses must manage information as an important product, capitalize on

knowledge as a principal asset and by so doing survive and prosper in the digital

economy [23] in which datawarehouses play an essential role. Consequently, one of

the main obligations of information technology professionals must be to ensure the

quality of the datawarehouses.

114

We believe that a key factor in relation to quality in datawarehouses is the quality

of the conceptual model. Using UML extensions for modelling datawarehouses at a

conceptual level, we have proposed a set of metrics for measuring the complexity of

the conceptual model obtained in the design of the datawarehouses. These metrics

will help designers to choose the best option between several alternative designs

(semantically equivalent).

Although we have theoretically validated the metrics used, this is only the first step

in the complete definition process of the metrics. By means of experiments, we are

currently validating empirically all the metrics presented in order to probe the

practical utility of the metrics. This empirical validation will enable us to discard or

refine these metrics.

It would also be advisable to study the influence of the different analysis

dimensions [1] on the cognitive complexity of the object-oriented model; as well as

the repercussion of using packages in the conceptual modelling of complex and

extensive datawarehouses in order to simplify their design [32]

Acknowledgements

This research forms part of the CALDEA (TIC 2000-0024-P4-02) project financed by

the General Subdirection for Research Projects of the Spanish Ministry of Science

and Technology.

References

1. Abelló, A., Samos, J. and Saltor, F. Understanding Analysis Dimensions in a

Multidimensional Object-Oriented Model. 3rd International Workshop on Design

and Management of Data Warehouses (DMDW´2001). Interlaken (Switzerland)

(2001).

2. Abelló, A., Samos, J. and Saltor, F. YAM

(Yet Another Multidimensional Model):

An extension of UML. International Database Engineering & Applications

Symposium (IDEAS´02) July 2002. Mario A. Nascimento, M. Tamer Özsu, Osmar

Zaïne (eds.). IEEE Computer Society Press, (2002) 172-181.

3. Adamson, C. and Venerable, M. Data Warehouse Design Solutions. John Wiley and

Sons, USA. (1998)

4. Basili V. and Weiss D. A Methodology for Collecting Valid Software Engineering

Data, IEEE Transactions on Software Engineering 10, 728-738 (1984)

5. Basili V. and Rombach H. The TAME project: towards improvement-oriented

software environments, IEEE Transactions on Software Engineering, 14(6), 728-738

(1988)

6. Briand, L.C., Morasca, S. and Basili, V. Property-based software engineering

measurement. IEEE Transactions on Software Engineering. 22(1). pp.68-85. (1996)

7. Bouzeghoub, M, Fabret, F. and Galhardas, H. Datawarehouse refreshment. Capitulo 4

in Fundamentals of Data Warehouses. Ed. Springer. (2000)

8. Bouzeghoub, M. and Kedad, Z. Quality in Data Warehousing. En: Information and

database quality. Kluwer Academic Publishers (2002)

115

9. Cabbibo, L., Torlone, R. A logical approach to multidimensional databases. Sixth

International Conference on Extending Database Technology (EDBT’98), Valencia.

Spain Lecture Notes in Computer Science 1377, Springer-Verlag, pp 183-197. (1998)

10. Calero, C., Piattini, M. and Genero, M. Empirical validation of referential integrity

metrics”, Information and Software Technology, 43(15), 949-957 (2001)

11. Calero, C., Piattini, M., Pascual, C. and Serrano, M.A. Towards Data Warehouse

Quality Metrics, Actas del 3rd Workshop on Design and Management of Data

Warehouses (DMDW'01) (2001)

12. Cavero, J.M., Piattini, M., Marcos, E., and Sánchez, A.. A Methodology for

Datawarehouse Design: Conceptual Modeling. 12th International Conference of the

Information Resources Management Association (IRMA2001), Toronto, Ontario,

Canada. (2001)

13. Celko, J. Don´t Warehouse Dirty Data. Datamation, 15 octubre, (1995) 42-52.

14. Chaudhuri, S. and Dayal, U. An Overview of Data Warehousing and OLAP

Technology. ACM SIGMOD Record 26(1) (1997)

15. English, L., Information Quality Improvement: Principles, Methods and

Management, Seminar, 5

Ed., Brentwood, TN: Information Impact International,

Inc., (1996).

16. Fenton N., Neil M. Software Metrics: a Roadmap. Future of Software Engineering,

Ed. Anthony Finkelstein, ACM, 359-370. (2000)

17. Genero M. Defining and Validating Metrics for Conceptual Models. Ph.D. Thesis,

University of Castilla-La Mancha. (2002)

18. Genero, M., Olivas, J., Piattini, M., Romero, F. Using metrics to predict OO

information systems maintainability. Proc. of 13

International Conference on

Advanced Information Systems Engineering (CAiSE’01). Lecture Notes in Computer

Science 2068, 388-401. (2001)

19. Genero, M., Jiménez, L., Piattini, M. A Controlled Experiment for Validating Class

Diagram Structural Complexity Metrics. Proc. of the 8th International Conference on

Object-Oriented Information Systems (OOIS´2002). Lecture Notes in Computer

Science 2425, 372-383. (2002)

20. Golfarelli, M., Maio, D., Rizzi, S. Conceptual design of data warehouses from E/R

schemes. 31

Hawaii International Conference on System Sciences. (1998)

21. Golfarelli, M., Rizzi, S. “Designing The Data Warehouse: Key Steps and Crucial

Issues”. Journal of Computer Science and Information Management, Vol 2, N. 3.

(1999)

22. Harinarayan, V., Rajaraman, A., Ullman, J. D. Implementing Data Cubes Efficiently.

Proc. of the 1996 ACM SIGMOD International Conference on Management of Data,

Jagadish, H. V. and Mumick, I. S. (eds.), pp. 205-216. (1996)

23. Huang, K-T., Lee, Y.W., Wang, R.Y. Quality Information and Knowledge. Prentice

Hall, Upper Saddle River. (1999)

24. Inmon, W.H. Building the Data Warehouse, second edition, John Wiley and Sons,

USA. (1997)

25. ISO, ISO International Standard ISO/IEC 9126. Information technology – Software

product evaluation. ISO, Geneve. (2001)

26. Jarke, M., Lenzerini, M., Vassiliou, Y., Vassiliadis, P. Fundamentals of Data

Warehouses, Ed. Springer. (2000)

27. Kimball, R.. The Data Warehouse Toolkit. John Wiley & Sons. (1996)

28. Kimball, R., Reeves, L., Ross, M., Thornthwaite, W. The Data Warehouse Lifecycle

Toolkit, John Wiley and Sons, USA. (1998)

29. Labio, W., Quass, D., Adelberg, B. Physical Database Design for Data Warehouses.

Thirteen International Conference on Data Engineering, IEEE Computer Society,

Birmingham, UK, pp. 277-288. (1997)

116

30. Loshin D. Enterprises Knowledge Management: The Data Quality Approach.

Morgan Kauffman, San Francisco (California) (2001)

31. Luján-Mora, S., Trujillo, J., Song, I-Y. Extending UML for Multidimensional

Modeling. 5th International Conference on the Unified Modeling Language (UML

2002), LNCS 2460, 290-304. (2002)

32. Luján-Mora, S., Trujillo, J., Song, I-Y.. Multidimensional Modeling with UML

Package Diagrams. 21st International Conference on Conceptual Modeling (ER

2002), LNCS 2503, 199-213.

33. Poels G., On the Formal Aspects of the Measurement of Object-Oriented Software

Specifications, Ph.D. Thesis, Faculty of Economics and Business Administration.

Katholieke Universiteit Leuven, Belgium, 1999

34. Redman, T.C. Data Quality for the Information Age. Artech House Publishers,

Boston (1996)

35. Sapia, C., Blaschka, M., Höfling, G., Dinter, B. Extending the E/R Model for the

Multidimensional Paradigm. ER Workshops 1998, Singapore, Lecture Notes in

Computer Science (LNCS), vol. 1552, pp. 105-116, (1998).

36. Serrano, M., Calero, C., Coimbra, C., Piattini, M. Métricas de calidad para

almacenes de datos. Proceedings of the VI Jornadas de Ingeniería del Software y

Bases de Datos (JISBD´2001), Ciudad Real, Díaz, O., Illarramendi, A. and Piattini, M.

(eds.), pp. 537-548 (2001)

37. Serrano, M., Calero, C., Piattini, M. Validating metrics for datawarehouses. IEE

Proceedings SOFTWARE, Vol. 149, 5, 161-166 (2002)

38. Serrano, M., Calero, C., Piattini, M. Experimental validation of multidimensional

data models metrics, Proc of the Hawaii International Conference on System

Sciences (HICSS’36), IEEE Computer Society (2003)

39. Suppes P., Krantz D., Luce, R., Tversky A. Foundations of Measurement:

Geometrical, Threshold, and Probabilistic Representations, 2, San Diego, Calif.,

Academic Press. (1989)

40. Tryfona, N., Busborg, F., Christiansen, G.B. starER: A Conceptual Model for Data

Warehouse Design. Proceedings of the ACM Second International Workshop on Data

Warehousing and OLAP (DOLAP’99), Kansas City, USA, pp. 3-8, (1999).

41. Trujillo, J., Palomar, M., Gómez, J., Song, I-Y. Designing Data Warehouses with

OO Conceptual Models. IEEE Computer, Special issue on Data Warehouses, 34 (12),

66 - 75. (2001)

42. Vassiliadis, P. Data Warehouse Modeling and Quality Issues. Ph.D. Thesis. National

Technical University of Athens. (2000)

43. Weyuker, E.J. Evaluating software complexity measures. IEEE Transactions on

Software Engineering. 14(9). pp.1357-1365. (1988)

44.

Whitmire, S.A. Object Oriented Design Measurement. Ed. Wiley. (1997)

45. Zuse, H. A Framework of Software Measurement. Berlin. Walter de Gruyter. (1998)

117