Stability in Context-Aware Pervasive Systems:

a State-Space Modeling Approach

Amir Padovitz

, Arkady Zaslavsky

, Seng Wai Loke

and Bernard Burg

School of Computer Science and Software Engineering, Monash University,

Caulfield East, VIC 3145, Australia

Abstract. This paper proposes a conceptual framework for context-aware-

systems, inspired by the state-space modeling approach and proposes the con-

cept of Stability as a means to characterize pervasive systems. We pro-

vide a collection of concepts concerning context, including Stability of context-

aware pervasive systems and show how these concepts can be used in modeling

context and actively maintaining stability and adaptation in a pervasive system.

We experimentally evaluate these concepts using a genetic algorithm in a

Smart Presentation Theatre scenario.

1 Introduction

Context-Aware pervasive systems are becoming increasingly important and emerging

research has begun to look at context-aware systems more generally, independently

of specific applications, including context middleware and toolkits [2,1] and ontology

to provide vocabularies to describe context [1,2,3].

Such pervasive systems can be described as proactive, highly dynamic context-aware

and adaptive systems [13, 6]. The more sensitive a pervasive system is to external

(not controlled by and outside the defined boundaries of a system [6]) influences,

more adaptation is generally required and less confidence might be gained in its abil-

ity to operate smoothly in the long run.

Research in pervasive computing and in particular in context-awareness has not

yet addressed in a generic way the problem of adapting to changing situations includ-

ing events that are not recognizable by the particular application. In adaptation, many

applications make use of human user interaction to guide the system in the adaptation

process [4, 8], which can often be too intrusive or too complex to be handled by a

user [11]. In addition, the pervasive system’s general state and the implication of this

state over its present and future functioning have so far been ignored.

Many current applications deal only with a finite set of foreseeable situations,

each employing specific methods to handle or adapt to well known predefined situa-

tions. Much of the effort is centered on correct reasoning of context and using speci-

We thank HP Labs for financial sponsorship and collaboration on this work.

Padovitz A., Zaslavsky A., Wai Loke S. and Burg B. (2004).

Stability in Context-Aware Pervasive Systems: a State-Space Modeling Approach.

In Proceedings of the 1st International Workshop on Ubiquitous Computing, pages 129-138

DOI: 10.5220/0002675901290138

 SciTePress

fied reaction to a changing context (e.g. changing mobile phone configuration accord-

ing to predefined user states). A fundamental problem that arises is the inability to

respond to events that cannot be classified to any known context. Such applications

are reactive in nature and not proactive, i.e. they react, or change their behavior once

new context is detected. This type of activity may suffice in simple well-foreseeable

and well-understood scenarios; however, in dynamic, perhaps highly distributed, and

with high degree of context uncertainty, the success of such approach will be at most,

limited. Furthermore, none investigate the general higher-level state of the pervasive

system as a whole. In dynamic and context-sensitive pervasive systems, it may be

critical to be able to internally balance or counter-affect external harmful changes,

and proactively sustain long-term operability of the pervasive system or other desir-

able situations.

In this paper, we propose and investigate the concept of Stability, as a means to

characterize a pervasive system. We make use of intuitions from the state-space

model of control systems [9] and propose steps towards application-independent

conceptual framework for context-aware systems. We show how pervasive system

stability and context stability can be represented and controlled when following our

conceptual framework approach and a methodology for maintaining stability. We

argue that our framework offers initial steps towards maintaining and controlling

stability and adaptability of dynamic context-aware systems. We illustrate and evalu-

ate our ideas by presenting an implementation of a Smart Presentation Theatre simu-

lation, using a genetic algorithm.

The rest of this paper is organized as follows. Section 2 presents the core concepts

of a modeling approach inspired by the state-space model of control systems [9]. We

continue to develop the model in Section 3 and discuss the concepts of stability, con-

trol and adaptation in pervasive environments and how they relate to our model. Sec-

tion 4 discusses use cases and describes implementation details of a genetic algorithm

used for adaptation and stabilization of a context-aware pervasive system. Experi-

mental evaluation for adaptation of a Smart Presentation Theatre scenario is presented

in Section 5. We conclude in Section 6.

2 A Model for Context State and Space

There are many dimensions of context. Context can be hierarchically structured

[12] and/or categorized into different domains (e.g. social, location-based, physio-

logical, etc. [5, 11]) and can denote different levels of abstraction, depending on the

desired situation to be modeled and the types of available sensorial and virtual infor-

mation. While models for context representation attempt to handle the complexity of

context by logical categorization [e.g. 5, 12], there is a need to create a more formal

model for context representation. We present a conceptual model, which is a step

towards formalizing context and can be used separately or in conjunction with any

higher-level context categorization or structural scheme.

We distinguish between the current contextual state (context state) of a system

and the broader definition of the context to which the current state belongs. Context

can be represented as an object in a multidimensional Euclidean space, termed situa-

130

tion subspace, in which each dimension represents a static domain of values that are

allowed for a specific context attribute (e.g. sensor input). At any given time, a con-

text state resides within a sub-region in the situation subspace, consisting of a domain

of tolerable values (inferred at the previous time interval and that never exceed the

situation subspace regions of values) in which the state is permitted to fluctuate and

still represent a valid state of a specific context.

Let the symbols C and R denote context state and situation subspace respectively.

Let the symbols a,

a and

a denote attribute, attribute’s value and attribute’s range

of values, respectively. We define

),...,,(

aaaC = as a context state i, de-

fined over a collection of N attribute-values, where each value

a corresponds to an

attribute

a . Similarly,

),...,,(

aaaR =

represents a situation subspace i,

consisting of N regions of values for these attributes. A region

a is defined as a set

of elements V that satisfies a predicate P, i.e.

a = {V |P(V)}. For example, in nu-

merical form the accepted region would often describe a domain of permitted real

values for an attribute

a . We examine other aspects of this model such as operators

that assist in defining, reasoning and manipulating context in [10].

The technical approach of representing context in terms of state and space, such as

the one discussed above, requires an ability to characterize attribute values numeri-

cally. While some attributes can be naturally represented in numeric form, others are

better conveyed semantically. We have addressed this issue in [10] where we dis-

cussed a technique borrowed from the relational database model that enables us to

quantitatively specify values and domain of values that correspond to a variety of

attributes, including semantic ones. We also employ application specific ontology to

map semantic values into the conceptual model. While sometimes overheads of inter-

preting semantics for context representation outweigh the benefits of this type of

representation (and therefore will not be used), in other cases the ability to model

context numerically enables us to apply useful techniques over context that require

values quantification. One such case is in control and adaptation of context-aware

pervasive systems. In particular, the model lends itself well for techniques from state-

space theory of control of linear systems that make use of analysis of the context state

trajectory.

3 The concept of Stability in pervasive systems

Describing the condition of a system that is distributed over disparate locations as

well as describing and/or controlling the state of a specific contextual situation within

such distributed system is hard to achieve and necessitate general approach that can

achieve this. We propose the notion of Stability in a pervasive environment as a

means to characterize a pervasive system by reflecting the distributed system’s state

as well as to reveal the status or confidence in a specific context by observing its

stability, thereby triggering control and adaptation operations.

131

While we make use of concepts from the state-space model of control theory for

maintaining context stability and control, many of its techniques cannot be used as

they require mathematical modeling of system behavior, such as defining set of dif-

ferential equations. Pervasive systems are complex and their exact behavior is often

hard to formulate. We therefore make use of the concepts but apply new techniques

(different from control theory) to uphold these concepts.

We conceive a context state (either defined to denote the overall system state or a

particular contextual situation) as fluctuating within a predefined situation subspace.

The position of the context state within the subspace and its Euclidean distance from

a predefined vector, termed ideal state reflects the degree of stability of the situation.

An ideal state is a context state that best corresponds to a specific context, judged by

the system’s developer, often having attribute values in the middle of the accepted

region for each attribute in the situation subspace.

In general, we state that the closer a context state is to the edges of the situation

subspace, a lesser degree of stability is gained, and the closer it is to the ideal state, a

greater degree of stability is gained, for that particular contextual situation. This char-

acterization considers the distance that is required for a context state to be better as-

sociated with another context (when moving away from the particular situation sub-

space boundaries).

By representing context-aware systems in terms of state, space and tolerable fluc-

tuation regions we gain the ability to perform more autonomic and generic adaptation

and control processes, in which systems that partially control their environments (i.e.

affecting either directly or indirectly the sensed data) can response to changes in the

context state by trying to produce reactions that will counter-affect or change the new

direction of the context state. A system that tries to maintain the stability of a specific

context would then strive to keep the dynamic fluctuation (in terms of position in

space) of the context state as close as possible to the defined ideal state of that situa-

tion subspace.

We use the following definitions in relation to stability.

Def 1. A context-aware pervasive system is said to be locally stable at time

t iff the

context state is contained within the situation subspace region of values and that

Kstateideal

<−

, where

ideal and

state denote the ideal state and the

context state at time

t , respectively and K denotes a predefined scalar value.

A context-aware pervasive system is locally unstable if it is not locally stable.

Def 2. A context-aware pervasive system is said to be globally stable under a situa-

tion subspace i at time

t iff the context state is locally stable and a minimal histori-

cal context state trajectory from time

tt < until

t can be estimated with reasonable

accuracy, where reasonable is application specific, to a function that is contained

within a situation subspace i. In other words, the context state continuously fluctuates

within the situation subspace boundaries.

132

Def 3. A context-aware pervasive system is said to be globally stable at time

t iff a

minimal historical context state trajectory from time

tt < until

t can be estimated

with reasonable accuracy, where reasonable is application specific, to a function that

is contained within all known situation subspaces. In other words, the context state

continuously fluctuates within all the situation subspaces boundaries, and may occa-

sionally be locally unstable.

3.1 Methodology for maintaining stability

We use the following methodology steps for maintaining stability of a context-aware

system with our modeling approach.

1. Identify situations that are desirable to be kept stable.

2. Identify available attributes that may be used in reasoning about these situations.

3. Identify regions of values of these attributes, corresponding to the situations.

4. Identify ideal context states for each situation.

5. Identify operations that may have direct or indirect influence over the situation

and attributes.

6. Examine the degree of a situation stability with respect to the following meas-

urements:

6.1 Distance between the context state and ideal context state.

6.2 Position of the context state with respect to the tolerable fluctuation region.

6.3 Relevance of attributes distribution that make up the context state.

7. Compute operations that balance any deviation from stable state by observing the

measurements in section 6.

4 Use cases and experimental evaluation

We can make use of the articulated concepts as a generic way for stabilizing and

adapting context-aware systems to chosen context. Consider a Smart House applica-

tion that tries to perfectly accommodate residents’ needs. We can conceive of several

important contextual situations, such as ‘Subject Sleeping’, ‘Subject Awakening’ or a

general ‘Comfort’ context. Each situation can be defined with a set of goals (e.g.

desired light level, temperature level, noise level) and the current state can be inferred

by sensorial data and denoted as context state. The system would then try to maintain

the stability of the chosen situation by adapting and affecting the context state to

match an ideal state defined for the particular situation. For example, in a ‘Comfort’

situation the system strives to maintain partly dimmed lights, half closed drapes, soft

music and a 21 Deg. temperature. When the system identifies a need to change the

situation, say move to a ‘Sleeping’ situation, it uses the same methodological steps

with a different stability goal, situation subspace and ideal state, e.g. would strive to

maintain minimum noise level, turned-off lights and closed drapes.

This kind of representation and methodology assist us to define general rules for

adaptation also in cases when circumstances do not allow perfect match between

133

ideal state and context state and thereby reflect less than perfect stability for a desired

situation. For example, if an obstacle obstructs the drapes from closing, the system

would infer imperfect stability of the desired context and would strive to reach perfect

stability. When the obstacle is removed, the drapes will be automatically closed, as

the system strives to maintain perfect stability. We can extend this rather simple ex-

ample to much more complex situations that require high degree of adaptation, char-

acterized by many unpredictable events that need to be dealt with, automatically. In

such cases, describing contextual situations in terms of state, spaces and stability

provides a generic and useful way to abstract complex adaptation goals and maintain

ongoing ideal system operability.

In our implementation we focused on a system that tries to maintain a current de-

sirable context, in the best possible way, in face of a changing environment. We

added the need to strive for context stability while considering application constraints

and resource limitations (due to changing environment and time limits) at that given

time.

We have chosen a Smart Presentation Theatre scenario, in which the system tries

to maintain optimal conditions for the ongoing presentation context. In other words, it

tries to maintain stability of the ‘Presentation’ situation subspace. The system con-

trols appliances that affect the presentation condition such as

a (‘light power’),

a (‘air condition level’),

a (‘speakers volume’) and

a (‘projector activity’). When

a change in the environment occurs, such as electric power failure followed by an

activation of a limited energy producer backup-generator in the building, or a change

in the departmental budget plan that affects the allowed power consumption of the

Smart Presentation Theatre, the system must adapt accordingly and change the system

behavior in the best possible way under the new resource limitation. This example

illustrates how our concepts apply to more complex situations that are constrained by

resource limitations with changes that are often unpredictable and may have variable

degree of influence over the system.

4.1 A Genetic algorithm approach

As our goal was to quickly find a sufficiently good solution (in case of changing

conditions during live presentation) in a relatively large space of possible solutions,

and we were after a generic solution that could be utilized according to different re-

sources and application constraints, we have developed a genetic algorithm that tradi-

tionally addresses these needs well [7]. Other techniques for finding optimal solutions

under constraints are also valid, as the use of a generic algorithm in this section is

mainly for purposes of demonstrating the usage and suitability of the state-space

model in gaining stability and performing adaptation.

4.2 General structure

In the Smart Presentation Theatre scenario, a genetic solution is a combination of

power consumption of the various appliances and consists of four units of data, corre-

134

sponding to light power, air condition level, speakers’ volume and projector activity.

Each unit value in this solution describes a valid activity level (and is mapped to a

power consumption value) for each of the above attributes. The mapping of the appli-

ances activity level to resource consumption), the resource limitation, and the applica-

tion constraints are determined externally by a context stabilizing application.

For a solution to be valid it must conform to the scenario’s resource limitation. We

denote

V as a locus (unit) value in a valid solution that comprises N units, such that

the following expression is observed:

RV ≤

∑

where

denotes the resource

limitation and both

R and

V are of the same domain of values. We assumed that

when the ideal amount of resource is not available (such as in the present scenario),

solutions that utilize less than the available limited resource are less fit solutions.

Consequently, for optimization, the algorithm observes the following rule when creat-

ing random solutions and when performing crossovers and mutations operations:

RV =

∑

where

R denotes the resource limitation and both

R and

V are of

the same domain of values.

The algorithm uses the state-space modeling approach and the methodology for main-

taining stability in the selection and fitness evaluation process. It represents the sys-

tem in state-space terms and computes solutions’ fitness according to measurements

suggested in the methodology for maintaining stability. In the following subsection

we briefly discuss the Fitness evaluation operation of the algorithm.

4.3 Fitness evaluation

During population regeneration, genetic crossover operations are activated on the

more fitted solutions in the population. Such solutions yield better result in terms of

application needs and constraints, thus, are chosen for recombination in the next gen-

eration. The algorithm produces Fitness evaluation according to the specific applica-

tion constraints. In the Smart Presentation Theatre scenario three rules were articu-

lated in order to produce desirable Fitness evaluation:

1. As more attribute values (e.g. air conditioning level = 23 Degrees) are within a

calculated range of values, i.e. within calculated tolerable fluctuation regions of

the corresponding attributes, a higher contribution to the Fitness is gained.

2. The smaller the Euclidean distance of the solution’s state from the ideal state, a

higher contribution to the Fitness is gained.

3. The smaller the diversity (in terms of normalized location in space) between the

different attributes, a higher contribution to the Fitness is gained.

All three rules were given equal importance.

The motivation for the above rules is the following.

135

1. The system’s optimal desire is that all attributes will be within tolerable fluctua-

tion regions so a locally stable and perfect match between the context and context

state is gained.

2. For the same reason as in 1, the closer the solution is to the ideal state a better

degree of stability and context matching is gained. Note however, that rule 1 and

2 are separate and may contradict one another, as a combination of attributes val-

ues outside but close enough to the tolerable fluctuation regions may yield a

smaller distance from the ideal state, than a combination partly containing attrib-

utes inside the regions. For example,

may be within the region but the others

are outside and very far from the ideal state.

3. A high normalized diversity between the different attributes may create undesir-

able solutions such as having ideal lighting but freezing temperatures.

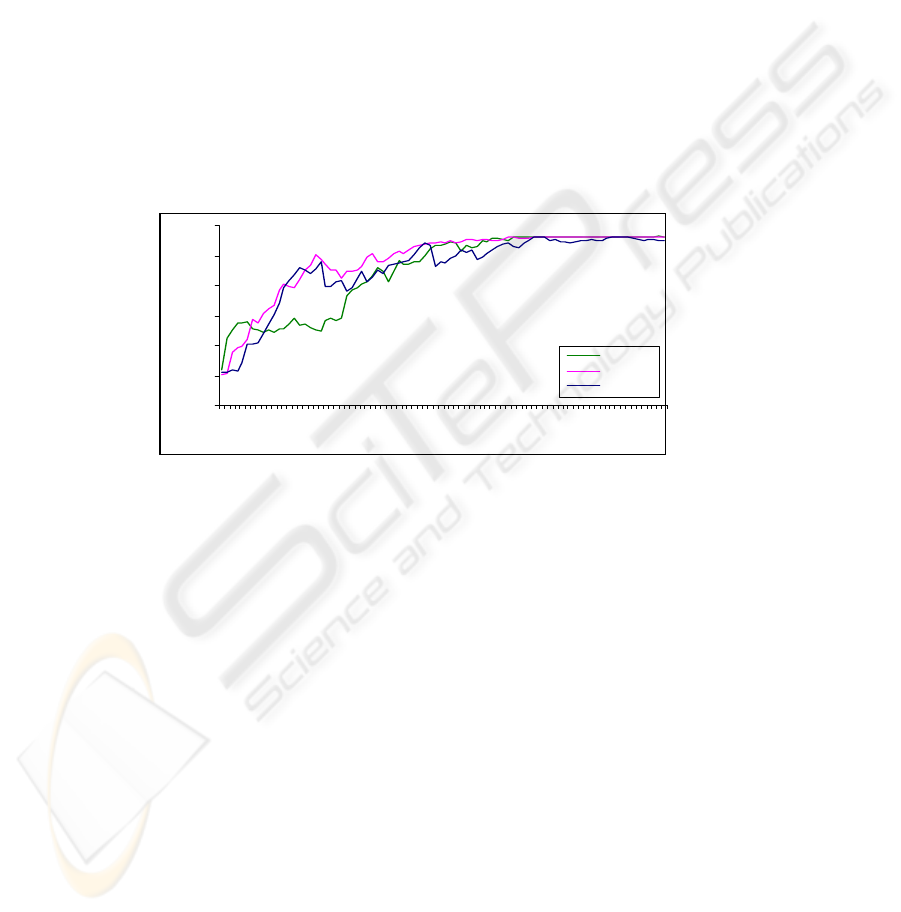
Convergence of the population mean fitness is shown in figure 1, for three crossover

rates. This behavior was observed during the Smart Presentation Theatre experimen-

tation. The population’s mean fitness tends to grow, and stabilize approximately after

55 generations and finds a locally ideal combination of attribute values.

Fig.1. Mean fitness convergences to locally best solution

5 Smart Theatre experimental run

We implemented a Context-Stabilizer prototype application that is responsible for

maintaining optimal conditions for the ‘presentation’ context. The prototype adapts to

changes in the environment by utilizing the genetic algorithm suggestions for an

optimal appliances activity. Figure 2 denotes a simulation of a power-failure during

presentation time. At first, all the appliances operate smoothly, with a context state

identical to the ideal state, which means that theatre lighting, air conditioning level

and speakers and projector activity are optimal. An electric power failure momentar-

ily drops the power consumption to zero. A first backup generator is then activated in

the building but only provides limited electricity power (we assumed an immediate

generator activation). The system then atomically resorts to the algorithm (configured

with population size = 100 and number of generations = 100) to find an optimal com-

bination for the appliances’ activity level, governed by the system needs and under

the new power limitations.

6.5

7.5

8.5

generations

mean fitness

Pc = 0.7

Pc = 0.5

Pc = 0.3

136

The result is plotted in figure 2 and is just below the ideal state tolerable regions.

Finally, a second small generator is activated and the system adapts to operate the

different electric appliances in the best possible way.

0.5

1.5

2.5

1 1019283746556473829110010911812713

Fig.2. Power failure scenario

6 Conclusion

In this paper we have introduced a set of concepts, inspired by the state-space

model of control systems that represents context in a scheme of situation subspace,

context state and tolerable fluctuation regions. We have introduced the idea of stabil-

ity in a pervasive system and presented implementation details and experimental

evaluation of some of the concepts discussed in the paper.

We believe that the approach described in this paper provides a new perspective

on context-aware pervasive systems and has practical impact in modeling, reasoning

and manipulating context as well as offering steps towards a unified conceptual

framework for context representation. The notion of a stable pervasive system is

becoming more important, as pervasive systems become more distributed and com-

plex and consequently, less manageable and less predictable. Our approach is well

suited for characterizing and controlling (in the sense of adapting and stabilizing)

large scale, distributed, pervasive systems and can impact the future development of

pervasive systems and adaptation processes.

We intend to continue and formalize a generic model and relate it to ontology

that would specify sets of situation subspaces for different domains. We will also rely

on ontology in developing operators that would map semantic attribute values into

numerical ones, so that we gain the ability to handle contexts that are more naturally

defined over semantic domains, rather than numeric. In future work we will apply the

concepts discussed in this paper for existing more complex scenarios, in areas such as

communication in heterogeneous environments and an emergency evacuation system.

Normed state

generator 2

generator

Ideal state tolerable region

137

References

1. Campbell R. H., Ranganathan A., A middleware for Context-Aware Agents in Ubiquitous

Computing Environments, ACM/IFIP/USENIX International Middleware Conference, Rio

de Janeiro, Brazil, June 2003.

2. Chen H., Finin T., Anupam J., An Intelligent Broker for Context-Aware Systems, Ubicomp

2003, October 2003.

3. Chen H., Finin T., Anupam J. An Ontology for Context-Aware Pervasive Computing Envi-

ronments, Workshop on Ontologies and Distributed Systems, IJCAI-2003, Acapulco, Mex-

ico, August 2003.

4. 5. Flinn J., Satyanarayanan M., Energy-aware adaptation for mobile applications, at 17th

ACM Symposium on Operating Systems and Principles. Kiawah Island, SC, December,

1999.

5. Huadong W., Mel S., Sevim A. Sensor Fusion for Context Understanding, IEEE Instrumen-

tation and Measurement, Technology Conference, Anchorage USA, May 2002.

6. Lieberman H., Selker T., Out of context: Computer systems that adapt to, and learn from,

context, CHI 2000, ACM Conference on Human Factors in Computing Systems, The

Hague, Netherlands, 2000.

7. Mitchell M., An Introduction to Genetic Algorithms, The MIT Press, Cambridge, Massa

chusetts, Sixth printing 1999, CH 5, pg 155 – 178.

8. Noble, B.D., Satyanarayanan, M., Narayanan, D., Tilton, J.E., Flinn, J., Walker, K.R. Agile

Application-Aware Adaptation for Mobility, at 16th ACM Symposium on Operating Sys-

tems Principles. Saint-Malo, France, October, 1997.

9. Ogata K., State Space Analysis of Control Systems, Prentice-Hall, Englewood Cliffs, N. J.

1967.

10. Padovitz A., Loke S. W., Zaslavsky A., Towards a Theory of Context Spaces, Workshop

on Context Modeling and Reasoning, at 2nd IEEE International Conference on Pervasive

Computing and Communication (PerCom'04), Orlando, Florida, March 2004.

11. Satyanarayanan M., Pervasive Computing: Vision and Challenges, IEEE PCM August

2001, pp. 10-17.

12. Schmidt A., Beigl M., Gellersen H. W., There is More to Context than Location, Workshop

on Interactive Applications of Mobile Computing, Rostock, Germany, November 1998.

13. Zaslavsky A. Adaptability and Interfaces: Key to Efficient Pervasive Computing, NSF

Workshop series on Context-Aware Mobile Database Management, Brown University,

Providence, January 2002.

138