Features Generation and Stochastic Geometry
Nikolay G. Fedotov, Luydmila A. Shul’ga
1
Penza State University, ul. Krasnaya 40, Penza, 440026 Russia
Alexander V. Moiseev
All–Russian Distance institute of finance & economics, ul. Kalinina 33B, Penza, 440052
Russia
Abstract: Application of stochastic geometry methods to pattern recognition
is analyzed. The paper is based on Trace-transformations of original images
introduced in [1] into images on the Mobius band. Trace–transformation is a
new geometrical transformation, which is connected with image scanning on
complex trajectories, including random parameters trajectories. Based on this
new geometric transformation, a new approach to the construction of features
independent of images' motion or their linear transformations is advanced. A
prominent characteristic of the group of features under consideration is that we
can represent each of them as a consecutive composition of three functionals.
1 Introduction
In pattern recognition, one traditionally distinguish the formation of features and
the decision procedure. In literature on cybernetics the situation has evolved
historically that the overwhelming majority of works on pattern recognition are
devoted to the decision rules and there are practically no works on the formation of
features. By a common view, this is explained by the fact that the process of feature
formation is empirical and depends on the intuition of a designer of a recognition
system. The approach in terms of stochastic geometry developed in [1] makes it
possible to fill this gap and, along with the constructive theory of features, to give
practical methods for generation of a large number of new features of image
recognition. Such a strong shift of the accent from decision rules to the new features
of recognition brings this approach closer to neurocomputing.
In [1], it was proposed to use as the features o
f image recognition the probabilities
of geometric events, i.e., the results of interaction of geometric objects (intersections,
covering, etc.). The role of geometric objects is played, on the one hand, by complex
trajectories of scanning with random parameters (segments, lines, curves, figures,
etc.) and, on the other hand, the fragments of the image to be recognized. The
structure of such recognition systems is considered, as well as the examples of
1
This work is supported by Human Capital Foundation
G. Fedotov N., A. Shul’ga L. and V. Moiseev A. (2004).
Features Generation and Stochastic Geometry.
In Proceedings of the 4th International Workshop on Pattern Recognition in Information Systems, pages 169-175
DOI: 10.5220/0002677201690175
Copyright
c
 SciTePress

specific technical implementations. We also consider the possible extensions of the
principal method for recognition based on the stochastic geometry. One of the
extensions is connected with the complication of the observations of a random event,
the intersection of the line of the beam trace and the image, i.e., with the application
of more complex features of recognition.
In this paper, we present the fundamentals of a new theory of formation of
recognition features that depend neither on motions of images nor on affine
transformations. The distinguishing feature of the group of features under
consideration is the representation of each of them in the form of a consecutive
composition of three functionals.
Consider the input grid of the recognition device, by which we mean the scanned
part of the image plane. In this part of the plane, a certain image is located, while the
rest of the plane is a background. Thus, the image is finite. Consider a random straight
line l which may cross the image. Let us assume that the intersection of the straight
line l and the image allows us to calculate a certain number g characterizing their
mutual location. Making a series of random tossing of the straight line l on the plane,
we obtain the sample for the random quantity g. Further, we can determine some
empirical characteristic n of the random quantity g. The described procedure is to be
implemented in the radio electronic system that performs the image recognition [1].
The mathematics of the procedure considered above was intensively studied in
stochastic geometry. It was found that, under certain conditions, the characteristic n
can have explicit geometric meaning. More important is that being easily
implemented in hardware, this idea can serve as a starting point for obtaining new
pattern recognition features both in theoretical analysis and in practice.
On the basis of the formulas presented in [1], the recognition criteria are
constructed. Only binary images are considered (black figures against the white
background).
(1) Consider the image in the form of the piecewise differentiable curve which can
be the boundary of a figure. Let g be the number of intersections of this curve with a
random straight line l. Then, the mathematical expectation Mg is proportional to the
length of the curve.
(2) Consider the image in the form of a convex figure. This can be the convex hull
of another figure. Let g be the length of intersection of the convex figure with a
random straight line l. Then, the mean values Mg
0
, Mg
1
, and Mg
2
are proportional to
the perimeter, area, and the own potential of the homogeneous layer, respectively.
2 Trace–Transformation
The formulas presented above and their numerous analogs have the following
drawbacks for pattern recognition:
(1) the number of such formulas is limited, since there are not so many explicitly
expressed geometric characteristics while thousands or more features are required;
(2) the formulas are applicable only to binary images. The merits of these formulas
are the possibility of parallel calculations (several straight lines are processed at once)
and stochastic realization, the latter makes it possible to terminate the process once
170

the required accuracy is attained. In addition, the calculated features do not depend on
the motions of objects. It is known that features usually strongly depend on rotation
and shift of the object, while in many pattern recognition problems rotation and shift
of the objects are absolutely noninformative. In this paper, we propose the
generalization of the approach presented above in order to overcome its drawbacks
and to retain its merits and, in some sense, this generalization is complete.
Let F denote a finite image. If the straight line l is given, then the value g that
characterizes the mutual location of the straight line l and the image will be calculated
according to a certain rule T: g=T(l,F), the mapping T will be called a functional. The
desired property is the independence of calculations of the motions of the object;
therefore, the only requirement that we impose on T is formulated in the following
way. Suppose the image was shifted and a new image F' appeared as a result. Under
the same shift and rotation, the straight line l will pass into the straight line l', thus
remaining “frozen” into the image. It is required that T(l,F)=T(l',F'). This relation
must be true for all straight lines and all admissible images. This property is called a
complete invariance of the functional T. It should be noted that the notion of complete
invariance rather strongly rises the possibilities of pattern recognition, since it does
not necessarily concern the number of intersections, the length of secant, etc. For
example, for the color image of variable brightness one can find quite a few such
functionals. Thus, the range of functionals and processed images is substantially
enlarged.
Similar to stochastic geometry, the random quantity g=T(l,F) is defined, whose
distribution does not depend on shifts and rotations of an image. Therefore, the
numerical characteristics of this random quantity once again may serve as features of
images which are determined by special technical devices and systems. The drawback
of the new family of features is the initial absence of the clear geometric meaning;
moreover their discriminating power is not known in advance. However, this is not of
particular importance for pattern recognition, because the experimental verification is
the deciding factor.
We note one more property of the completely invariant functional T (Trace). It is
not necessarily determined only by the section of an image by the straight line.
Another information can be invoked for its calculation, for example, the properties of
a neighborhood of this section.
In order to understand that the proposed generalization exhaust in a sense all its
capabilities, we present the theory of Trace-transformations. If the normal coordinates
are introduced on the plane, the straight line l is characterized by its distance p from
the origin and by the angle θ (accurate to within 2π ) of its direction vector
l= {(x,y) : xcos θ + ysin
θ },
l=l(θ,p), where x and y are the Cartesian coordinates on the plane. If we let the
parameter p take also the negative values, then l(θ,p)=l(θ+π,–p). Thus, the set of all
directed straight lines crossing the circle of radius R centered at the origin (the “grid”)
is uniquely parameterized by the set
Λ={(θ,p): 0≤θ≤π, –R≤p≤R}
under condition that the parameters (0,p) and (π,–p) define a single straight line. It
is seen that the set of the straight lines on the grid is topologically nothing else than
the Möbius band [2]. The set of numbers T(l(θ,p),F) depending on the point on the
Möbius band Λ is a certain image transformation called Trace-transformation. If, for
171

example, in the numerical analysis the Trace-transformation is represented by a
matrix, then we call the latter a Trace-matrix. If we direct the axis 0θ horizontally,
and the axis 0p vertically, then at the point θ
i
, p
i
the entry of the matrix with the
number (i,j) will be located, i.e, the value of T(l(θ
j
,p
i
),F). Here, θ
j
, p
i
are some values
of the uniform discrete grids on the indicated axes. The matrix is 2π–periodical in the
direction of the horizontal axis; moreover, at each interval of length π its columns are
turned over.
Let us additionally assume that if the straight line l does not cross the image, then
T(l,F) is a given number (for instance, 0) or other fixed element if the functional T is
not numerical. In this case, to the initial image F there corresponds Trace (F), a new
image (one can treat T(l(θ,p) as an image whose characteristics at the point (θ,p) are
its Trace-image).
Figure 1 explains the calculation of the Trace-transform. Here, obtaining the binary
function f(θ,p,t) of real variable under scanning of the straight line l is shown. The
function f(θ,p,•) is equal to 1 in the intervals (t
1
,t
2
) and (t
3
,t
4
) and takes on the value 0
in the others. Consider the functional T of given function, and define t as an
independent variable. Thus, we obtain g(θ,p)=Tf(θ,p,t). We call the function g the
result of the Trace-transform. For example, the functional Tf(θ,p,t) can be the
maximal value in the domain of definition of the function f(θ,p,•) In Figure 1a, it is
the quantity t
2
– t
1
. If we define the similar functional Tf(θ,p,t) for all straight lines
scanning the Chinese hieroglyph in Figure 1a under different angles θ and different
distances p, we obtain the Trace-matrix (Figure 1b).
Fig. 1. The process of scanning of original image and corresponding Trace-transform
Let us briefly consider the changes of the image T(F) under shifts and rotations of
the source image F. If the initial image is rotated, its Trace-image shifts along the
horizontal axis 0θ. If, on the other hand, the shift of the source image takes place by
some vector, then its image undergoes the following transformations. We better
present them in terms of the Trace-matrices. The columns remains unchanged at their
places, but may be shifted up or down. The vector of the shift determines the numbers
a and b such that the column with the coordinate θ
i
is shifted in the vertical direction
by acos(θ
i
– b). It should be noted that this description is completely strict only if the
172

Trace-matrix is assumed to be continuous, i.e., if i and j are continuous parameters.
The details of research and theoretical considerations can be found in [4].
The usual Euclidean measure dθdp is invariant to the indicated transformations,
therefore, the density of distribution of any function given on the Möbius band, in this
case, the function of the image, Trace (F), does not depend on the indicated
transformations.
There exists a wide class of problems, which are practically important. In such
problems pattern recognition is combined with the task of objects search. In this case,
as it can be seen in [1], the application of scanning with random parameters gives
much more advantages in ration “realibility of recognition to the time of recognition”
in comparison with determinate scanning. Random parameters scanning has also great
advantages in the analysis of random textures from the field of nanotechnologies. It is
shown in the report, that the realization of trace-transformation and triple features in
such a variant of scanning.
In discrete variant of calculations the result of trace-transformation is a matrix,
consisting of values t
ij
= T(l(θ
j
,p
i
),F). The parameters of the scanning straight line
form the two discrete set
Ω={p
1
,p
2
,…,p
n
},
Θ={θ
1
,θ
2
,…,θ
m
}.
With determinate scanning each element t
ij
of matrix is definite.
In set Ω and Θ we determine probabilities distribution by vectors ξ={ξ
1
,ξ
2
,…,ξ
n
},
η={η
1
,η
2
,…,η
m
}. Choosing the parameters of scanning by a random way according to
the given distributions, we get matrix of random values T
ij
, where
T
ij
0 t
ij
P
ij
1-ξ
j
η
i
ξ
j
η
i
The result of the action of functional P and Θ is a random value.
So, indication Π(F) is a random value, and it distribution is fully defined by
vectors ξ, η.
One can get minimum interval evaluations of indication Π(F) with less expenses
on scanning, choosing probability, distributions of parameters θ
i
and p
j
for the given
class of objects.
3 Triple features
Consider the formation of the triple features representing the consecutive
composition of three functionals Π(F)=Θ◦P◦T(F◦L(θ, p, t)). Each functional (Θ, P,
and T) acts on the functions of one variable (θ, p, and t, respectively). For each of the
three functionals, one can conceive tens distinct concretizations satisfying the
required conditions. Therefore, we immediately obtain thousands of new features
invariant to motions.
The functional T corresponding to the Trace-transform, was considered above in
detail. In the discrete variant of computations, the result of this transform or the
Trace-transform T(F◦l(θ,p,t)) is a matrix whose entries are, for example, the values of
brightness of the image F at the intersections with the scanning line l(θ,p). The
173

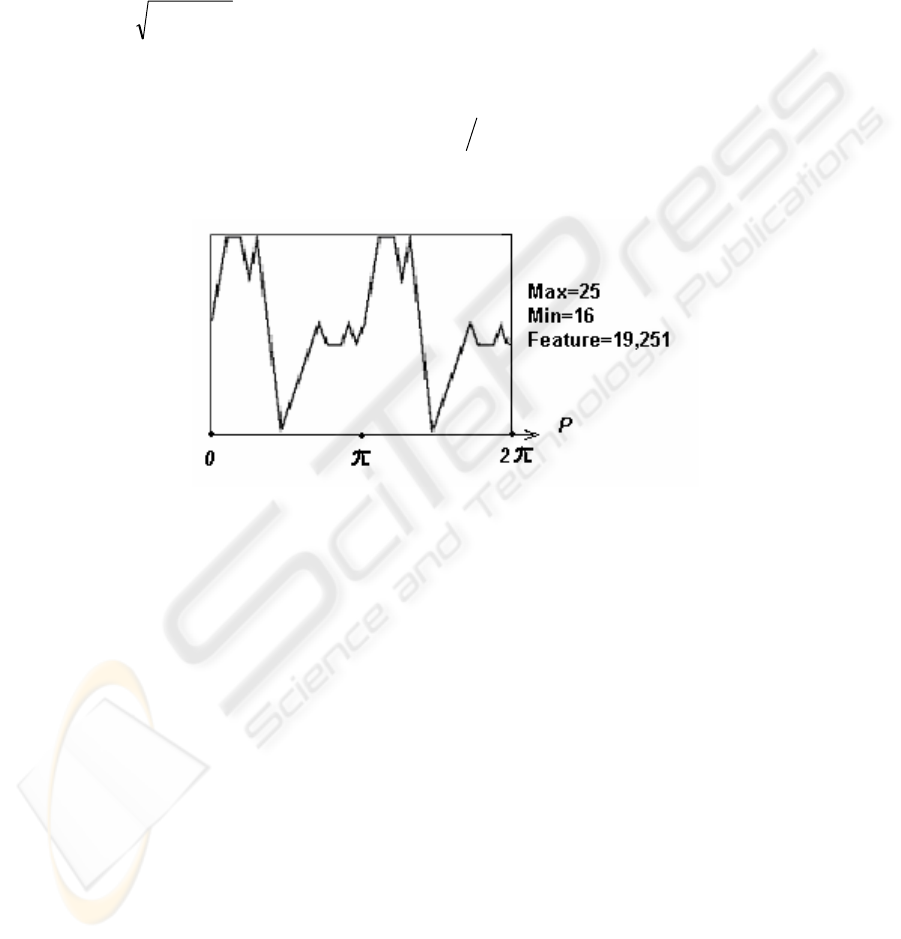
parameters of the scanning line p determine the position of this entry in the matrix.
The further calculation of the feature consists in the consecutive processing of the
columns of the matrix with the use of the functional P which we call a diametric
functional. The “Norm” functional, a standard Euclidean norm of the function
∫
= dpphPh )(
2
was used as the diametric one. Another example of the diametric
functional is the functional called “Max”. This is the maximal value of the function in
the column of the Trace-matrix, and the “Mid” functional. The latter is the standard
center of gravity of masses calculated as follows:
∫∫
= dpphdppphPh )()( .
The result of application of the functional P (“Norm”) of the Trace-matrix (Figure
1b) is a 2π-periodic curve shown in Figure 2.
Fig.2. Operation of the Diametric and Circus functionals
At the next stage, the transformations on the curve must be performed by using the
Θ-functional, which is called circular. The “Log” functional was used as a variant of
the circular functional Θ:
∫
+=Θ θθ dhh |1)(ln| .
To overcome the redundancy caused by generation of a large number of features,
the procedure of formation of the minimal set of most efficient recognition features
was applied on the basis of the Karhunen–Loeve expansion. This makes it possible to
increase the speed of action of recognition systems and use the most simple decision
rules.
4 Conclusions
The described theory of triple features makes it possible to generate a large
number, actually thousands, of features that prove to be useful only for the pattern
recognition problems with a multiple structure of classes, e.g., for the problem of
174

recognition of hieroglyphs. The obtained features can be used for the recognition of
grayscale and color images.
The considered triple recognition features can be calculated in the highly parallel
process. Similar to the features formed by the neural networks, these features has no
meaning set in advance, their selection is carried out in the course of machine
experiment taking into account only their usefulness for the classification.
There exists a wide class of problems, which are practically important. In such
problems pattern recognition is combined with the task of objects search. The
application of scanning with random parameters gives much more advantages in
ration “reliability of recognition to the time of recognition” in comparison with
determinate scanning. Random parameters’ scanning has also great advantages in the
analysis of random textures from the field of nanotechnologies. It is shown in the
report, that the realization of trace-transformation and triple features in such a variant
of scanning.
References
1. Fedotov, N.G., Metody stokhasticheskoi geometrii v raspoznavanii obrazov (Methods of
Stochastic Geometry in Pattern Recognition), Moscow: Radio i Svyaz’ (1990)
2. Fedotov, N.G., Estimation of Accuracy of the Stochastic Method of Measurements,
Izmeritel’naya tekhnika, (1996) N9
3. Fedotov, N.G. and Tuzhilov, I.V., Neurocomputing Technology for Generation of Features
for Pattern Recognition, Informatika-Mashinostroenie, issue 1(19) (1998) 38–42
4. Fedotov, N. G. and Shulga, L.A., New Ways to Form Features for Pattern Recognition on
the Basis of Stochastic Geometry, Proc. 12th Scandinavian Conf. on Image Analysis,
Bergen (2001) vol. I. II 373–380
175