DISTRIBUTED GRADIENT

FOR MULTI-ROBOT MOTION PLANNING

Gerasimos Rigatos

Unit of Industrial Automation

Industrial Systems Institute

26504, Rion Patras, Greece

Keywords:

multi-robot system, cooperative behavior, stochastic search algorithms, distributed gradient, Lyapunov stabil-

ity.

Abstract:

Distributed stochastic search is proposed for cooperative behavior in multi-robot systems. Distributed gradient

is examined. This method consists of multiple stochastic search algorithms that start from different points in

the solutions space and interact to each other while moving towards the goal position. Distributed gradient is

shown to be efﬁcient when the motion of the robots towards the goal position is described by a quadratic cost

function. The algorithm’s performance is evaluated through simulation tests.

1 INTRODUCTION

In the recent years there has been growing interest

in multi-robot systems (Guo and Parker, 2002). As

the cost of robots goes down and as robots become

more compact the number of military and industrial

applications of multi-robot systems increases. Possi-

ble industrial applications of multi-robot systems in-

clude hazardous inspection, underwater or space ex-

ploration, assembling and transportation. Some ex-

amples of military applications are guarding, escort-

ing, patrolling and strategic behaviors, such as stalk-

ing and attacking.

Of primary importance in the design of multi-robot

systems is motion planning through obstacles. To

solve this problem distributed gradient algorithms

are proposed. These are an extension of the poten-

tial ﬁelds methods which have have been previously

used for robot path-planning (Khatib, 1986)-(Reif and

Wang, 1999). The potential of each robot consists of

two terms: (i) the cost V

due to the distance of the

i-th robot from the goal state, (ii) the cost due to the

interaction with the other M − 1 robots. Moreover,

a repulsive ﬁeld, generated by the proximity to obsta-

cles, is taken into account. The differentiation of the

aggregate potential provides the kinematic model for

each robot. It is proved that the velocity update equa-

tion is equivalent to a distributed gradient algorithm.

The convergence to the goal state is studied with the

use of Lyapunov stability theory. It is shown that in

the case of a quadratic cost function V

the mean po-

sition of the multi-robot system converges to the goal

state x

∗

while each robot stays in a bounded area close

to x

∗

. These results are also of interest for research in

the area of particle systems where similar problems of

cooperative behavior are studied (Levine and Rappel,

2000).

The structure of the paper is as follows: In Section

2 elements of stochastic search algorithms are

summarized and distributed gradient is proposed for

multi-robot motion planning. Stability analysis of the

distributed gradient algorithms is performed with the

use of Lyapunov theory. In Section 3 the performance

of the distributed gradient algorithm in the problem

of multi-robot motion planning is tested through

simulation tests. Finally, in Section 4 concluding

remarks are stated.

2 DISTRIBUTED STOCHASTIC

Motion planning of multi-robot systems can be solved

with the use of distributed stochastic search algo-

rithms. These can be multiple gradient algorithms

that start from different points in the solutions space

and interact to each other while moving towards the

goal position. Distributed gradient algorithms, stem

Rigatos G. (2005).

DISTRIBUTED GRADIENT FOR MULTI-ROBOT MOTION PLANNING.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 59-65

DOI: 10.5220/0001154000590065

 SciTePress

from stochastic search algorithms treated in (Duﬂo,

1996) if an interaction term is added:

(t + 1) = x

(t) + γ

(t)[h(x

(t)) + e

(t)]+

j=1,j6=i

g(x

− x

), i = 1, 2, · · · , M

(1)

The term h(x(t)

) = −∇

) indicates a local

gradient algorithm, i.e. motion in the direction of

decrease of the cost function V

) =

(t)

(t).

The term γ

(t) is the algorithm’s step while the

stochastic disturbance e

(t) enables the algo-

rithm to escape from local minima. The term

j=1,j6=i

g(x

− x

) describes the interaction be-

tween the i-th and the rest M − 1 stochastic search

algorithms. Convergence analysis based on the

Lyapunov stability theory can be stated in the case of

distributed gradient algorithms. This is important for

the problem of multi-robot motion planning.

2.1 Kinematic model of the

multi-robot system

The objective is to lead a swarm of M mobile robots,

with different initial positions on the 2-D plane, to a

desirable ﬁnal position. The position of each robot

in the 2-D space is described by the vector x

∈ R

The motion of the robots is synchronous, without time

delays, and it is assumed that at every time instant

each robot i is aware about the position and the ve-

locity of the other M − 1 robots. The cost function

that describes the motion of the i-th robot towards the

goal state is denoted as V (x

) : R

→ R. The value

of V (x

) is high on hills, small in valleys, while it

holds ∇

V (x

) = 0 at the goal position and at lo-

cal optima. The following conditions must hold: (i)

The cohesion of the swarm should be maintained, i.e.

the norm ||x

− x

|| should remain upper bounded

||x

− x

|| < ǫ

, (ii) Collisions between the robots

should be avoided, i.e. ||x

− x

|| > ǫ

, (iii) Conver-

gence to the goal state should be succeeded for each

robot through the negative deﬁniteness of the associ-

ated Lyapunov function

) = ˙e

(t)

(t) < 0.

(Rigatos, et al., 2001). The interaction between the

i-th and the j-th robot is taken to be

g(x

−x

) = −(x

−x

)[g

(||x

−x

||)−g

(||x

−x

||)]

(2)

where g

() denotes the attraction term and is domi-

nant for large values of ||x

− x

||, while g

() denotes

the repulsion term and is dominant for small values of

||x

− x

||. Function g

() can be associated with an

attraction potential, i.e. ∇

(||x

− x

||) = (x

−

(||x

− x

||). Function g

() can be associated

with a repulsion potential, i.e. ∇

(||x

− x

||) =

− x

(||x

− x

||). A suitable function g() that

describes the interaction between the robots is given

by (Gazi and Passino, 2004)

g(x

− x

) = −(x

− x

)(a − be

−||x

−x

) (3)

where the parameters a, b and c are suitably tuned. It

holds that g

− x

) = −a, i.e. attraction has a lin-

ear behavior (spring-mass system) ||x

− x

||g

−

). Moreover, g

− x

) = be

−||x

−x

which

means that g

− x

)||x

− x

|| ≤ b is bounded.

Applying Newton’s laws to the i-th robot yields

˙x

= v

˙v

= U

(4)

where the aggregate force is U

= f

+ F

. The term

= −K

denotes friction, while the term F

the propulsion. Assuming zero acceleration ˙v

= 0

one gets F

= K

, which for K

= 1 and m

= 1

gives F

= v

. Thus an approximate kinematic model

˙x

= F

(5)

According to the Euler-Langrange principle, the

propulsion F

is equal to the derivative of the total

potential of each robot, i.e.

= −∇

) +

i=1

j=1,j6=i

(||x

−

|| − V

(||x

− x

||)]} ⇒ F

= −∇

)} −

j=1,j6=i

[∇

(||x

−x

||)−∇

(||x

−x

||)] ⇒

= −∇

)} +

j=1,j6=i

[−(x

−

(||x

− x

||) + (x

− x

(||x

− x

||)] ⇒

= −∇

)} +

j=1,j6=i

g(x

− x

Substituting in Eq. (5) one gets Eq. (1), i.e.

(t + 1) = x

(t) + γ

(t)[−∇

) + e

(t +

1)] +

j=1,j6=i

g(x

− x

), i = 1, 2, · · · , M , with

(t) = 1, which veriﬁes that the kinematic model

of a multi-robot system is equivalent to a distributed

gradient search algorithm.

2.2 Stability of the multi-robot

system

The behaviour of the multi-robot system is deter-

mined by the behaviour of its center (mean of the

vectors x

) and of the position of each robot with

respect to this center. The center of the multi-robot

system is given by ¯x = E(x

) =

i=1

, there-

fore

¯x =

i=1

˙x

⇒

¯x =

i=1

[−∇

)−

ICINCO 2005 - ROBOTICS AND AUTOMATION

j=1,j6=i

(g(x

− x

))].

From Eq. (3) it can be seen that g(x

−x

) = −g(x

−

), i.e. g() is an odd function. Therefore, it holds that

(

j=1,j6=i

g(x

− x

)) = 0, and

¯x =

i=1

[−∇

)] (6)

Denoting the goal position by x

∗

, and the distance

between the i-th robot and the mean position of the

multi-robot system by e

(t) = x

(t) − ¯x the objective

of distributed gradient for robot motion planning can

be summarized as follows: (i) lim

t→∞

¯x = x

∗

, i.e.

the center of the multi-robot system converges to the

goal position, (ii) lim

t→∞

= ¯x, i.e. the i-th robot

converges to the center of the multi-robot system,

(iii) lim

t→∞

¯x = 0, i.e. the center of the multi-robot

system stabilizes at the goal position. If conditions (i)

and (ii) hold then lim

t→∞

= x

∗

. Furthermore, if

condition (iii) also holds then all robots will stabilize

close to the goal position.

It is known that the stability of local gradient algo-

rithms can be proved with the use of Lyapunov theory.

A similar approach can be followed in the case of the

distributed gradient algorithms given by Eq. (1) (Gazi

and Passino, 2004). The following simple Lyapunov

function is considered for each gradient algorithm:

⇒ V

||e

(7)

Thus, one gets

= e

˙e

⇒

= ( ˙x

−

¯x)e

⇒

= [−∇

) −

j=1,j6=i

g(x

− x

) +

j=1

∇

)]e

. Substituting g(x

−x

) from

Eq. (3) yields

= [−∇

) −

j=1,j6=i

−

)a +

j=1,j6=i

− x

(||x

− x

||) +

j=1

∇

)]e

⇒

= −a[

j=1,j6=i

−

)]e

j=1,j6=i

(||x

− x

||)(x

− x

)

−

[∇

) −

j=1

∇

)]

It holds that

j=1

− x

) = Mx

−

j=1

= M x

− M ¯x = M(x

− ¯x) = M e

therefore

= −aM ||e

j=1,j6=i

(||x

− x

||)(x

− x

)

−[∇

) −

j=1

∇

)]

(8)

It assumed that for all x

there is a constant ¯σ such

that

||∇

)|| ≤ ¯σ (9)

Eq. (9) is reasonable since for a robot moving on a 2-

D plane, the gradient of the cost function ∇

)

is expected to be bounded. Moreover it is known that

the following inequality holds:

j=1,j6=i

− x

)

≤

j=1,j6=i

≤

j=1,j6=i

b||e

Thus the application of Eq. (8) gives

≤aM||e

j=1,j6=i

(||x

− x

||)||x

− x

|| · ||e

|| +

||∇

) −

j=1

∇

)||||e

|| ⇒

≤aM||e

+ b(M − 1)||e

|| + 2¯σ||e

|| where it

has been taken into account that

j=1,j6=i

(||x

−x

||)

||e

||≤

j=1,j6=i

b||e

|| = b(M −1)||e

and from Eq. (9)

||∇

) −

j=1

∇

)||≤

||∇

)|| +

j=1

∇

)||≤

¯σ +

M ¯σ ≤ 2¯σ

Thus, one gets

≤aM||e

||·[||e

|| −

b(M − 1)

− 2

¯σ

] (10)

The following bound ǫ is deﬁned:

ǫ =

b(M − 1)

2¯σ

(b(M −1)+2¯σ) (11)

Thus, when ||e

|| > ǫ,

will become negative and

consequently the error e

= x

− ¯x will decrease.

Therefore the error e

will remain in an area of radius

ǫ i.e. the position x

of the i-th robot will stay in the

cycle with center ¯x and radius ǫ.

2.3 Stability in the case of a

quadratic cost function

The case of a convex quadratic cost function is exam-

ined, for instance

) =

||x

− x

∗

− x

∗

)

− x

∗

)

(12)

where x

∗

= [0, 0] is a minimum point

= x

∗

) = 0. The distributed gradient al-

gorithm is expected to converge to x

∗

. The robotic

vehicles will follow different different trajectories on

DISTRIBUTED GRADIENT FOR MULTI-ROBOT MOTION PLANNING

the 2-D plane and will end at the goal position.

Using Eq.(12) yields ∇

) = A(x

− x

∗

Moreover, the assumption ∇

) ≤ ¯σ can be

used, since the gradient of the cost function remains

bounded. The robotic vehicles will concentrate round

¯x and will stay in a radius ǫ given by Eq. (11).

The motion of the mean position ¯x of the vehicles is

¯x = −

i=1

∇

) ⇒

¯x = −

− x

∗

) ⇒

¯x − ˙x

∗

= −

∗

⇒

¯x − ˙x

∗

= −A(¯x − x

∗

)

The variable e

= ¯x−x

∗

is deﬁned, and consequently

˙e

= −Ae

⇒ ǫ

(t) = c

−At

+ c

(13)

with c

+ c

= e

(0). Eq. (13) is an homogeneous

differential equation, which for A > 0 results into

lim

t→∞

(t) = 0, thus lim

t→∞

¯x(t) = x

∗

. It is

left to make more precise the position to which each

robot converges.

2.4 Convergence analysis using La

Salle’s theorem

It has been shown that lim

t→∞

¯x(t) = x

∗

and

from Eq. (10) that each robot will stay in a cycle

C of center ¯x and radius ǫ given by Eq. (11). The

Lyapunov function given by Eq. (7) is negative

semi-deﬁnite, therefore asymptotic stability cannot

be guaranteed. It remains to make precise the area of

convergence of each robot in the cycle C of center ¯x

and radius ǫ. To this end, La Salle’s theorem can be

employed (Gazi and Passino, 2004), (Khalil, 1996).

La Salle’s Theorem: Assume the autonomous system

˙x = f(x) where f : D → R

. Assume C ⊂ D a

compact set which is positively invariant with respect

to ˙x = f(x), i.e. if x(0) ∈ C ⇒ x(t) ∈ C ∀ t

. Assume that V (x) : D → R is a continuous

and differentiable Lyapunov function such that

V (x) ≤ 0 for x ∈ C, i.e. V (x) is negative semi-

deﬁnite in C. Denote by E the set of all points in

C such that

V (x) = 0. Denote by M the largest

invariant set in E and its boundary by L

, i.e. for

x(t) ∈ E : lim

t→∞

x(t) = L

, or in other words

is the positive limit set of E. Then every solution

x(t) ∈ C will converge to M as t → ∞.

La Salle’s theorem in applicable in the case of the

multi-robot system and helps to describe more pre-

cisely the area round ¯x to which the robot trajectories

will converge. A generalized Lyapunov function

is introduced which is expected to verify the stability

analysis based on Eq. (10). It holds that:

V (x) =

i=1

) +

i=1

j=1,j6=i

(||x

−

|| − V

(||x

− x

||)} ⇒ V (x) =

i=1

) +

i=1

j=1,j6=i

{a||x

− x

− V

(||x

− x

||),

and

∇

V (x) = [

i=1

∇

)] +

i=1

j=1,j6=i

∇

{a||x

− x

− V

(||x

−

||)} ⇒ ∇

V (x) = [

i=1

∇

)] +

j=1,j6=i

− x

){g

(||x

− x

||) − g

(||x

−

||)} ⇒ ∇

V (x) = [

i=1

∇

)] −

j=1,j6=i

g(||x

− x

||)

and using Eq. (1) with γ

(t) = 1 yields ∇

V (x) =

− ˙x

, and

V (x) = ∇

V (x)

˙x =

i=1

∇

V (x)

˙x

⇒

V (x) = −

i=1

|| ˙x

≤ 0

(14)

Therefore, in the case of a quadratic cost func-

tion it holds V (x) > 0 and

V (x)≤0 and the set

C = {x : V (x(t)) ≤ V (x(0))} is compact and

positively invariant. Thus, by applying La Salle’s

theorem one can show the convergence of x(t) to the

set M ⊂ C, M = {x :

V (x) = 0} ⇒ M = {x :

˙x = 0}.

2.5 Stability in the case of a cost

function with local minima

The following multi-modal Gaussian cost function is

considered

) = −

j=1

−||x

−c

(15)

where c

∈ R

is the center of the i-th Gaussian,

∈ R

is the variance of the i-th Gaussian, and

∈ R deﬁnes if the Gaussian stands for hill (A

0) or a valley (A

< 0). The gradient of the multi-

modal Gaussian function in given by

∇

) =

j=1

− c

−||x

−c

(16)

The velocity of the i-th robot is given by Eq.(1)

˙x

= −∇

)−

−

j=1,j6=i

− x

)[g

(||x

− x

||) − g

(||(x

− x

)||)]

(17)

ICINCO 2005 - ROBOTICS AND AUTOMATION

while the velocity of the center of the multi-robot sys-

tem is given by Eq. (6)

¯x = −

∇

) ⇒

¯x = −

j=1

− c

−||x

−c

(18)

Eq. (18) does not give any information about the di-

rection of the center ¯x of the multi-robot system. Un-

der speciﬁc assumptions convergence to local minima

(valleys) or divergence from local maxima (hills) can

be shown. To this end , it is assumed that at t = 0

holds,

||x

(0) − c

||≤σ

, k : 1≤k≤N

||x

(0) − c

||≥σ

, k : 1≤j≤N

This means that the multi-robot system goes close to

the Gaussian with center c

and stays far from the

Gaussian with center c

. The following error deﬁni-

tion is given

= ¯x − c

(19)

and the Lyapunov function V

is consid-

ered. It holds that

= ( ˙e

)

⇒

¯x

⇒

= [−

j=1

− c

−||x

−c

Assuming that (x

−c

) < (e

)

, i.e. x

−c

< ¯x −c

i.e. the mean of the multi-robot system is closer to the

valley k yields

< −

j=1

−||x

−c

||e

Therefore, for A

< 0 it holds that

< 0 and the

multi-robot system will converge to the k-th Gaussian

center c

3 SIMULATION TESTS

In the conducted simulation tests the multi-robot sys-

tem consisted of 10 robots which were randomly ini-

tialized in the 2-D ﬁeld. Two cases were distin-

guished: (i) motion in an obstacle-free environment

(Fig. 1 - Fig. 2 and (ii) motion in an environment

with obstacles (Fig. 5 - Fig. 6). The objective was

to lead the robot swarm to the origin [x, y] = [0, 0].

To avoid obstacles, apart from the motion equations

given in Sections 2 repulsive forces between the ob-

stacles and the robots had to be taken into account.

The reactive robot behavior for obstacle avoidance

prevailed locally the motion laws which were derived

using potential ﬁelds theory. This means that the col-

lision avoidance was set to higher priority than main-

tenance of the cohesion of the robots swarm.

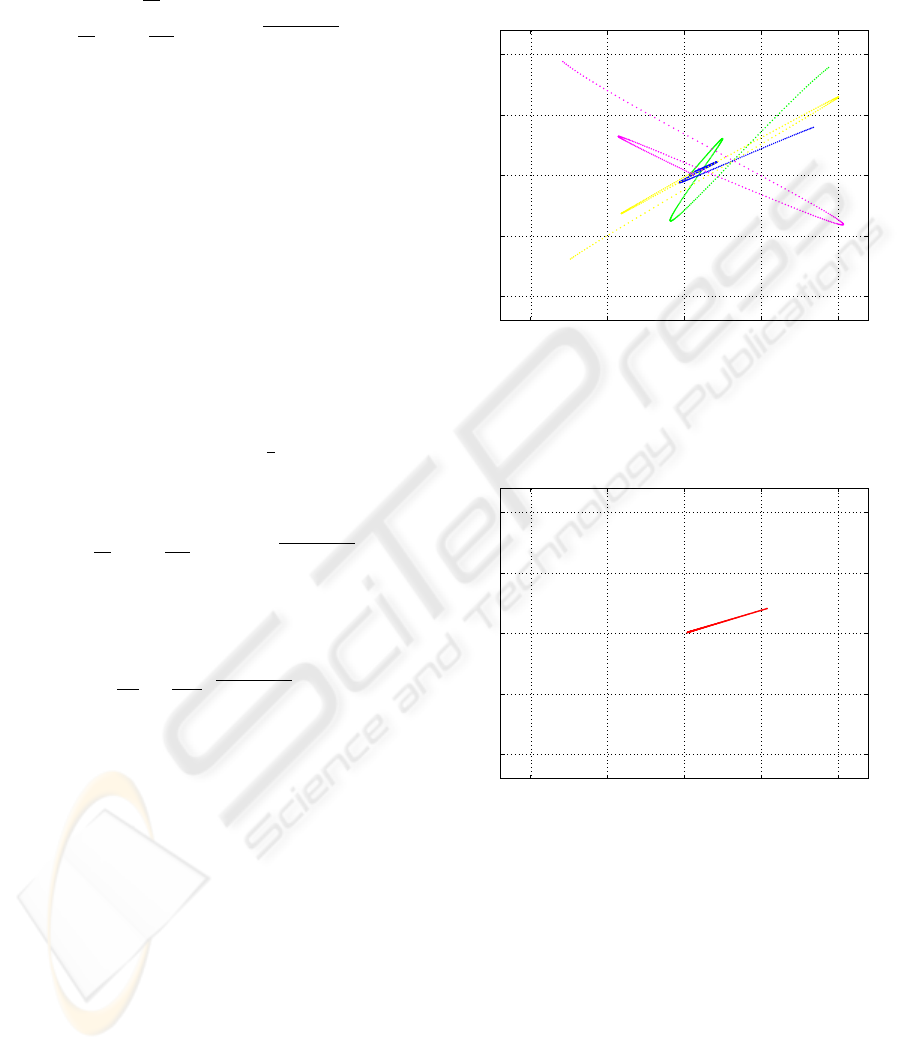
−10 −5 0 5 10

−10

−5

Figure 1: Motion of the individual robots in an obstacles-

free environment, considering a quadratic cost function.

−10 −5 0 5 10

−10

−5

Figure 2: Motion of the mean of the multi-robot system in

an obstacles-free environment, considering a quadratic cost

function.

For the motion in an obstacle-free environment, the

evolution of the aggregate Lyapunov function of the

multi-robot system, as well as of the Lyapunov func-

tions of the individual robots, is depicted in Fig. 3 and

Fig. 4.

When the multi-robot system evolved in an envi-

ronment with obstacles, the interaction between the

individual robots (attractive and repulsive forces)

had to be loose, so as to give priority to obstacles

avoidance. Therefore coefﬁcients a and b in Eq.

DISTRIBUTED GRADIENT FOR MULTI-ROBOT MOTION PLANNING

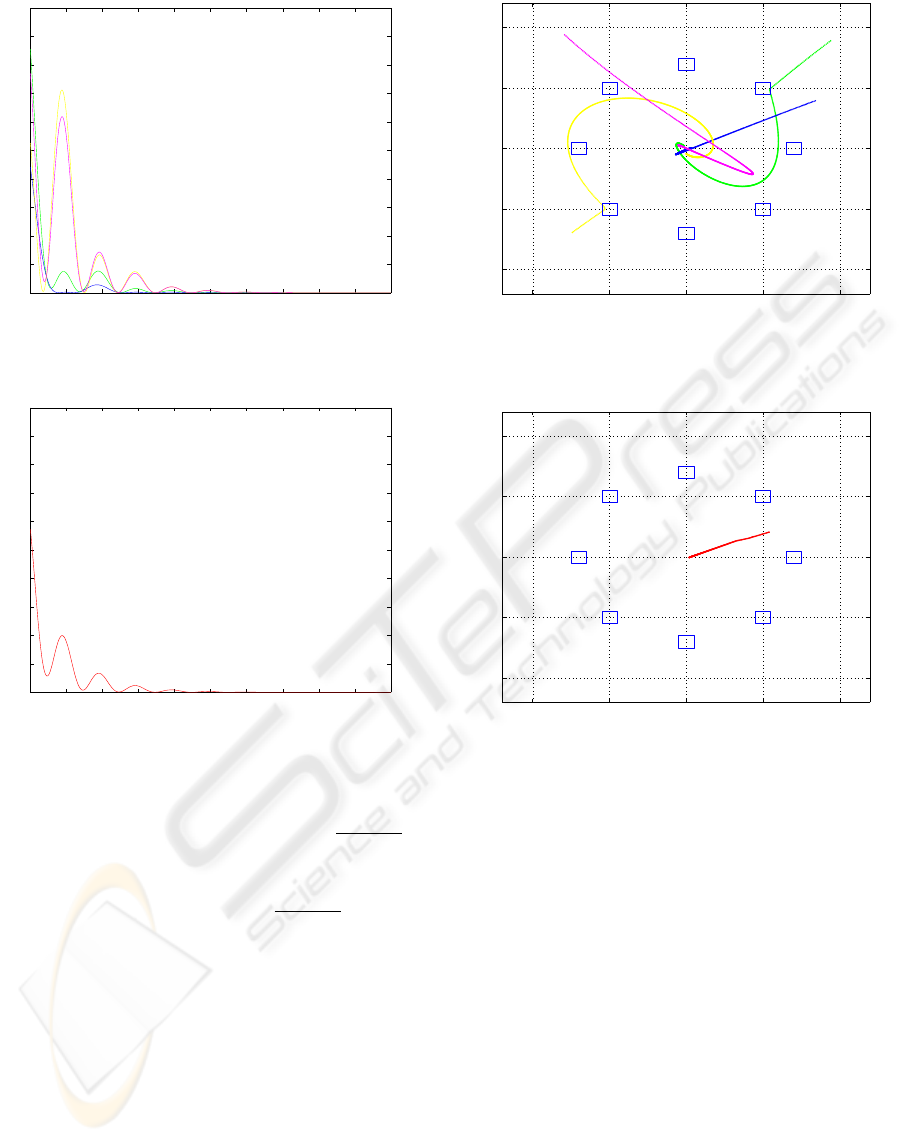
0 100 200 300 400 500 600 700 800 900 1000

100

time k

Lyapunov of the robots

Figure 3: Lyapunov function of the individual robots in an

obstacles-free environment.

0 100 200 300 400 500 600 700 800 900 1000

100

time k

Lyapunov of the mean

Figure 4: Lyapunov function of the mean of the multi-robot

system in an obstacles-free environment.

(3) g(x

− x

) = −(x

− x

)(a − be

||x

−x

)

were set to small values. The repulsive po-

tential due to the obstacles was calculated by

g(x

− x

) = −(x

− x

)(a − be

||x

−x

), where

was the center of the j-th obstacle.

The relative values of the parameters a and b that ap-

pear in the attractive and repulsive potential respec-

tively, affected the performance of the algorithm. For

a > b the cohesion of the robotic swarm was main-

tained and abrupt displacements of the individual ro-

bots were avoided.

For the motion in an environment with obstacles, the

evolution of the aggregate Lyapunov function of the

multi-robot system, as well as of the Lyapunov func-

tions of the individual robots, is depicted in Fig. 7

and Fig. 8 . Comparing to Fig. 3 and Fig. 4 the dif-

ferences are due to the smaller value of the attractive

force coefﬁcient a.

−10 −5 0 5 10

−10

−5

Figure 5: Motion of the individual robots in an environment

with obstacles, considering a quadratic cost function.

−10 −5 0 5 10

−10

−5

Figure 6: Motion of the mean of the multi-robot system in

an environment with obstacles, considering a quadratic cost

function.

4 CONCLUSIONS

In this paper the problem of distributed multi-robot

motion planning was studied. A M -robot swarm was

considered and the objective was to lead the swarm

to a goal position. The kinematic model of the robots

was derived using the potential ﬁelds theory. The po-

tential of each robot consisted of two terms: (i) the

cost V

due to the distance of the i-th robot from the

goal state, (ii) the cost due to the interaction with the

other M − 1 robots. The differentiation of the poten-

tial provided the kinematic model for each robot. It

was proved that the velocity update equation is equiv-

alent to a distributed gradient algorithm. The con-

vergence to the goal state was studied with the use

of Lyapunov stability theory. It was shown that in the

case of a quadratic cost function V

the mean position

of the multi-robot system converges to the goal state

ICINCO 2005 - ROBOTICS AND AUTOMATION

0 100 200 300 400 500 600 700 800 900 1000

100

time k

Lyapunov of the robots

Figure 7: Lyapunov function of the individual robots in an

environment with obstacles.

0 100 200 300 400 500 600 700 800 900 1000

100

time k

Lyapunov of the mean

Figure 8: Lyapunov function of the mean of the multi-robot

system in an environment with obstacles.

∗

while each robot stays in a bounded area close to

∗

Distributed gradient for multi-robot motion planning

was evaluated through simulation tests. It was ob-

served that when the multi-robot system was evolving

in an environment with obstacles, the interaction be-

tween the individual robots (attractive and repulsive

forces) had to be loose, so as to give priority to obsta-

cles avoidance. The performance of the method was

satisfactory. The algorithm succeeded cooperative be-

havior of the robots without requirement for explicit

coordination or communication.

REFERENCES

Guo Y. and Parker L.E. (2002), A distributed and optimal

motion planning approach for multiple mobile robots,

In: Proc. 2002 IEEE Intl. Conference on Robotics and

Automation, Washington DC, May 2002, pp. 2612-

2619.

Khatib O. (1986), Real-time obstacle avoidance for manip-

ulators and mobile robots, International Journal of Ro-

botic Research, vol. 5, no.1, pp. 90-99.

Rimon E. and Koditscheck D.E. (1991), Exact robot navi-

gation using artiﬁcal potential functions, IEEE Trans-

actions on Robotics and Automation, vol. 8, pp. 501-

518.

Reif J.H. and Wang H., Social potential ﬁelds: A distrib-

uted behvioral control for autonomous robots, Robot-

ics and Autonomous Systems, Elsevier, vol. 27, 1999,

pp.171-194.

Levine H. and Rappel W.J. (2000), Self-organization in sys-

tems of self-propelled particles, Physical Review E,

vol. 63.

Duﬂo M. (1996), Algorithmes stochastiques,

Math

ematiques et Applications vol. 23, Springer,

1996.

Rigatos G.G., Tzafestas S.G. and Evangelidis G.J. (2001),

Reactive Parking Control of a non-holonomic vehicle

via a fuzzy learning automaton, IEE Proc. on Control

Theory and Applications, vol. pp. 169-180.

Gazi V. and Passino K. (2004), Stability analysis of so-

cial foraging swarms, IEEE Transactions on Systems,

Man and Cybernetics - Part B: Cybernetics, vol. 34,

no. 1, pp. 539-557.

Khalil H. (1996), Nonlinear Systems, Prentice Hall.

Clerk M. and Kennedy J. (2002), The Particle Swarm-

Explosion, Stability, and Convergence in a Multi-

dimensional Complex Space, IEEE Transactions on

Evolutionary Computation, vol. 6, no. 1, pp. 58-73,

2002.

DISTRIBUTED GRADIENT FOR MULTI-ROBOT MOTION PLANNING