REAL TIME WEB AVAILABILITY OF STATISTICAL MODELS FOR

WATER LEVELS ALONG THE TEXAS COASTLINE

Alex Sadovski

Department of Computing and Mathematical Sciences, Texas A&M University–Corpus Christi

6300 Ocean Dr. Corpus Christi, TX 78412

Carl Steidley

Department of Computing and Mathematical Sciences, Texas A&M University-Corpus Christi

6300 Ocean Dr. Corpus Christi, TX 78412

Philippe Tissot

Department of Physical and Life Sciences, Texas A&M University-Corpus Christi

6300 Ocean Dr. Corpus Christi, TX 78412

G. Beate Zimmer

Department of Computing and Mathematical Sciences, Texas A&M University-Corpus Christi

6300 Ocean Dr. Corpus Christi, TX 78412

Keywords:

Harmonic analysis, prediction, tide chart, multivariate statistical modeling, linear regression, web, forecast,

water level.

Abstract:

Water level forecasts are essential to the success of trade and industry in the Gulf of Mexico, but present

forecasting methodologies do not provide accurate predictions for the Gulf Coast region. Tide charts produced

by harmonic analysis are the existing standard, but these charts only show the effect of astronomical forces

acting upon the water. While this proves to be an accurate predictor for most of the Atlantic and Paciﬁc Coasts,

water level changes along the Texas Coast are strongly effected by meteorological factors and thus require a

modiﬁed prediction model, rather than harmonic analysis alone. A web-based tool was created that combines

harmonic analysis with multivariate statistical modeling to predict water levels along the Texas Gulf Coast.

The result is a substantial improvement on the current model with forecasts available via the World Wide Web.

1 INTRODUCTION

The goal of our on-going research is to develop ef-

fective and reliable tools for predicting water levels in

the shallow waters of the Gulf of Mexico. Different

schemes that we are using for the prediction of water

levels include harmonic analysis, statistical models,

and neural networks. Multivariate statistical based

models of predictions of tides and neural network

predictions are under development at the Division of

Nearshore Research and Department of Computing

and Mathematical Sciences of Texas A&M Univer-

sity - Corpus Christi.

Due to the heavy dependence of trade and indus-

try along the Gulf of Mexico coast on water level

forecasts, accuracy in these forecasts is essential, but

the current standard forecasting methodologies do not

provide accurate predictions for this region. Tide

charts, produced by harmonic analysis and published

by the National Ocean Service, are the existing stan-

dard, but these charts only show the astronomical

forces acting upon the water. While this proves to be

an accurate predictor for major portions of the other

coasts, water level changes along the Texas Coast

are strongly effected by meteorological factors (Cox

et al., 2002) and thus require a modiﬁed prediction

model. A web-based tool was created that combines

harmonic analysis with multivariate statistical mod-

eling to predict water levels along the Texas Gulf

Coast. The result is a substantial improvement on the

tide charts with forecasts available via the web. Wa-

ter level data used to make these predictions is gath-

ered by the Texas Coastal Ocean Observation Net-

work (TCOON), which is managed by the Division

of Nearshore Research.

218

Sadovski A., Steidley C., Tissot P. and Beate Zimmer G. (2005).

REAL TIME WEB AVAILABILITY OF STATISTICAL MODELS FOR WATER LEVELS ALONG THE TEXAS COASTLINE.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 218-223

DOI: 10.5220/0001157502180223

 SciTePress

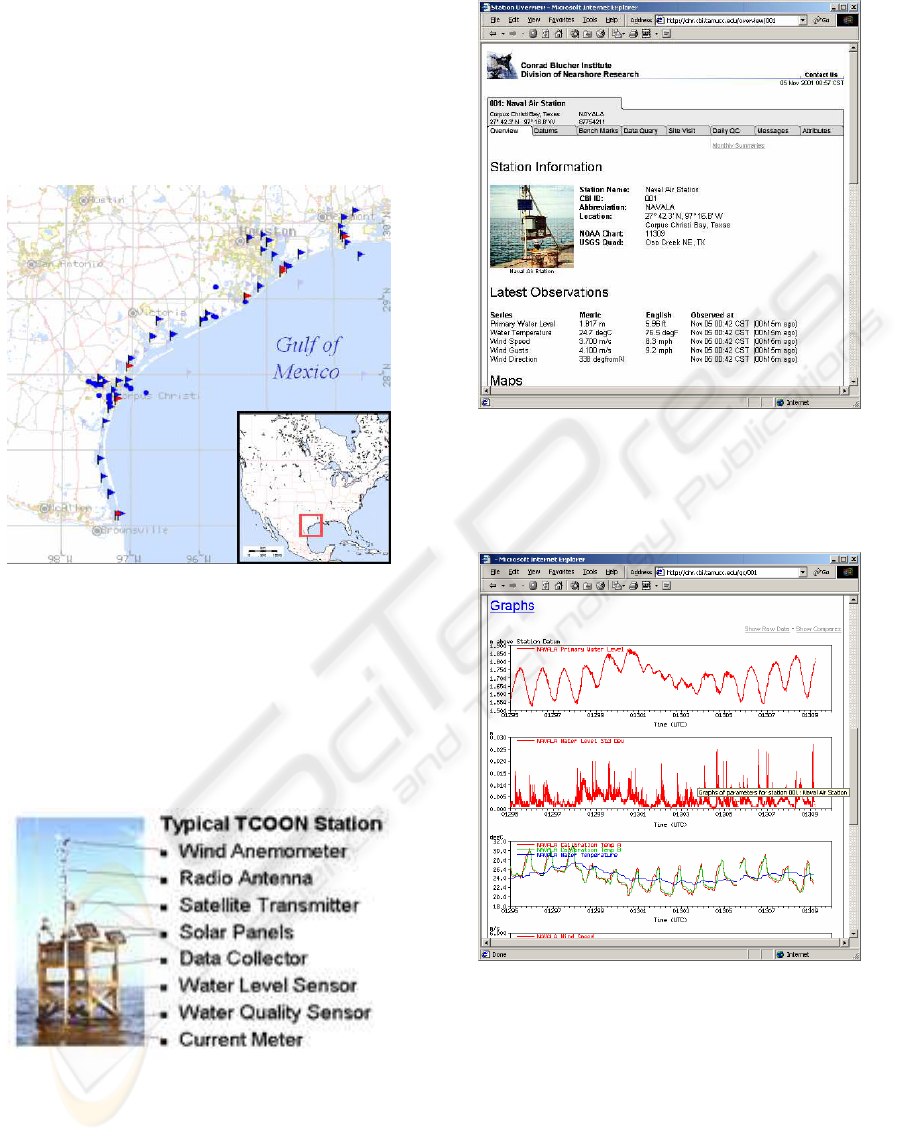
2 TEXAS COASTAL OCEAN

OBSERVATION NETWORK

The Texas Coastal Ocean Observation Network

(TCOON) started in 1989 and operates over 50 en-

vironmental data collection platforms along the Gulf

Coast, from Mexico to Louisiana (Fig.1). Primary

Figure 1: Map of TCOON Stations.

project sponsors include the Texas General Land Of-

ﬁce, Texas Water Development Board, U.S. Army

Corps of Engineers, and NOAA National Ocean Ser-

vice. TCOON stations (Michaud et al., 2001) mea-

sure and archive various measurements such as water

levels, wind speed and direction, temperature, salin-

ity, and barometric pressure (Fig. 2). TCOON follows

Figure 2: Typical TCOON station.

U.S. National Ocean Service standards for the instal-

lation of its stations and has a very useful real-time,

online database. TCOON data is valuable for tidal

datum, coastal boundaries, oil-spill response, naviga-

tion, storm preparation and response, as well as re-

search.

Figure 3: TCOON web site: top of the page about station

001: Naval Air Station.

Figure 4: TCOON web site: graphs of water levels, air and

water temperature data for Naval Air Station.

See Figures 3 and 4 for examples of TCOON web

pages. The screen depicted in Figure 3 contains the

latest measurements taken at the selected station. The

screen in Figure 4 depicts an illustration of graphical

representations of TCOON measurements in near-real

time.

REAL TIME WEB AVAILABILITY OF STATISTICAL MODELS FOR WATER LEVELS ALONG THE TEXAS

COASTLINE

219

3 HARMONIC ANALYSIS

According to the Tide and Current Glossary issued by

the National Ocean Service (NOS) in 2000, tide is de-

ﬁned as: The periodic rise and fall of a body of water

resulting from gravitational interactions between Sun,

Moon, and Earth

Thus, changes in water level from non-gravitational

forces are not “tides” but rather “water levels” which

can be deﬁned as:

Astronomical+Meteorological Forcing+Other Effects

Present forecasting methodologies do not provide ac-

curate predictions for the Gulf Coast region, because

of shallow waters in this part of the Gulf of Mexico.

The standard method for tide predictions is harmonic

analysis. Harmonic analysis (HA) (Sadovski et al.,

2003b) is represented by constituent cosine waves

with known frequencies based on gravitational or pe-

riodic forces.

h(t) = H

y,c

cos(a

t + e

y,c

− k

where

h(t) = elevation of water at time t

= frequency (speed) of constituent c

y,c

= node factors/equilibrium args

= datum offset

= amplitude of constituent c

= phase offset for constituent c

Figure 5: Comparison of water levels measured (red) and

predicted by harmonic analysis (green) at the Bob Hall Pier

Station for part of August 2002. It can be seen that tide

tables provide accurate forecasts when the inﬂuence of me-

teorological and other factors is small.

4 IMPROVEMENT OF

PREDICTIONS

Our goal is to develop and compare models forecast-

ing the difference between observed water levels and

Figure 6: Comparison of water levels measured (red) and

predicted by harmonic analysis (green) at the Rockport Sta-

tion for January to March 2002. The large inﬂuence of me-

teorological forcing can be observed throughout the period.

the harmonic predictions. Approaches considered in-

clude persistence model, multivariate statistical mod-

eling, and neural networks (Sadovski et al., 2003b),

(Tissot et al., 2002). The models are built and tested

based on the past observations and then applied to

predict future water level differences. The methodol-

ogy to develop and test the new model based on linear

regression is illustrated in Fig 7.

Harmonic

Analysis

Model





Recent

Obser-

vations

Recent

Diﬀerences





Coeﬃcients

Harmonic

Analysis

Forecasts





Predicted

Diﬀerences

Improved

Water

Level

Forecasts

2. Apply the Model to Produce Forecasts

Harmonic

Analysis

Model





Training

Set Obser-

vations

Diﬀerences

Linear

Regression

Coeﬃcients

1. Create the Model

Figure 7: Schematics Illustrating the methodology to de-

velop and test the new water level forecasting models.

We performed a factor analysis of water level data

for over 20 of the TCOON stations, one station at a

time, using water levels over a period of 48 hours with

measurements for every other hour as variables. Data

spanning nearly one year were used for each factor

analysis. The stations included deep water stations

such as Flower Garden near Houston and shallow wa-

ter stations such as Bob Hall Pier near Corpus Christi.

For Bob Hall Pier, four components extracted by Prin-

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

220

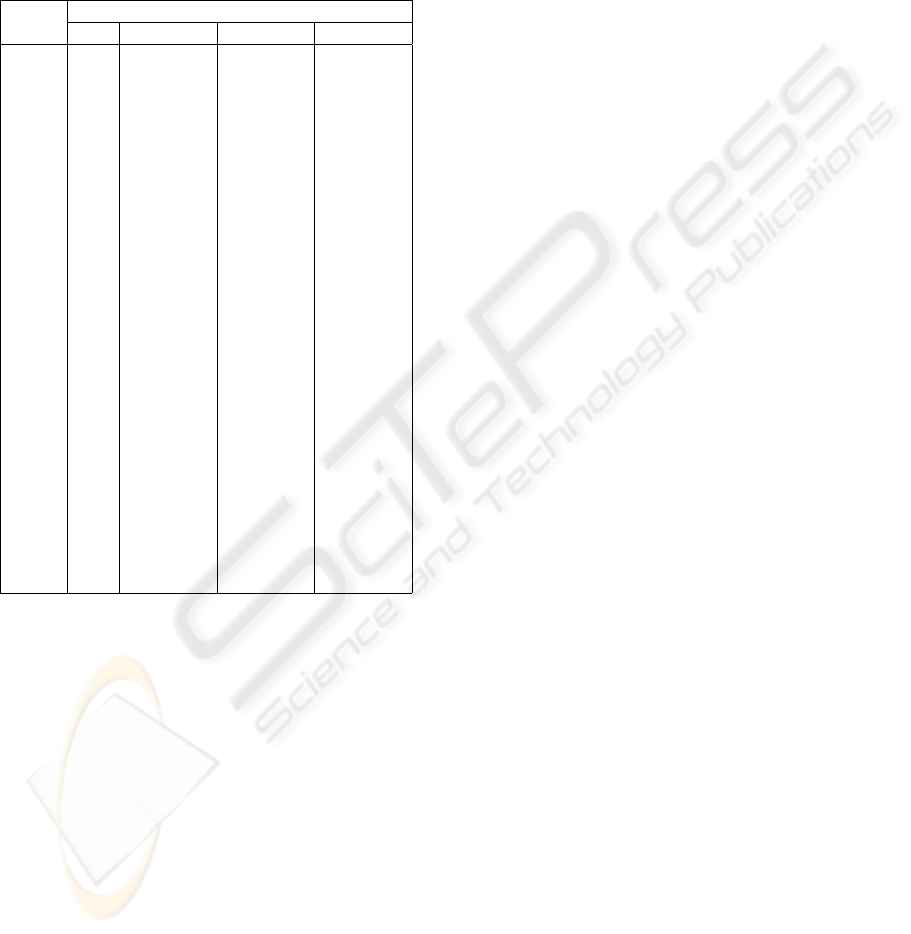
cipal Component Analysis explained 96.2% of the to-

tal variance of the data. A look at the correlation ma-

trix for the four main factors and the variables (Figure

8) shows all positive correlations in the column for

the ﬁrst component, indicating a non-periodic com-

ponent, whereas for example the pattern of the corre-

lation coefﬁcients for the second component shows a

periodic component.

Component

time t 1 2 3 4

0 .762 -.261 .452 -.276

-2 .777 -.437 .350 -.186

-4 .791 -.543 .160 -.120

-6 .804 -.551 -7.047E-02 -9.277E-02

-8 .815 -.455 -.284 -.113

-10 .825 -.278 -.426 -.174

-12 .833 -5.918E-02 -.462 -.253

-14 .840 .150 -.382 -.323

-16 .846 .303 -.205 -.354

-18 .851 .363 2.348E-02 -.332

-20 .854 .319 .247 -.256

-22 .856 .186 .410 -.139

-24 .857 8.896E-04 .470 4.746E-04

-26 .856 -.185 .411 .140

-28 .854 -.319 .248 .257

-30 .850 -.364 2.372E-02 .333

-32 .845 -.305 -.206 .354

-34 .840 -.153 -.383 .322

-36 .833 5.687E-02 -.464 .253

-38 .824 .276 -.429 .173

-40 .814 .455 -.287 .113

-42 .803 .551 -7.393E-02 9.279E-02

-44 .790 .545 .157 .120

-46 .776 .440 .348 .187

-48 .760 .265 .451 .277

Figure 8: Correlation matrix for the four main components

for Bob Hall Pier.

For the deep water station Flower Garden, ﬁve

main components explain 93.8% of the total variance

of the data. The ﬁrst two components for Flower

Garden are periodic and the third component has all

positive correlation coefﬁcients, indicating that it is a

non-periodic component. We found that at each sta-

tion tested, no more than 5 factors explain over 90%

of the variance for water levels. The periodic main

components could be called “astronomical”, the non-

periodic component that shows mainly in shallow wa-

ters could be called “weather”. For all stations in the

coastal shallow waters and estuaries we found the ﬁrst

component to be not periodical; hereweather is an im-

portant input for predictions. The other components

are periodical. For the stations on off-shore deep wa-

ters the ﬁrst two components are astronomical or pe-

riodical.

These conclusions assisted us in improving pre-

dictions in the shallow waters since the conclusion

suggested integrating a regression approach with har-

monic analysis. Namely, we use the idea that vari-

ations of water levels depend on two components -

a harmonic component (tides) and another compo-

nent which is affected by weather. The regression ap-

proach incorporates recent weather and the harmonic

analysis parts accounts for the astronomical compo-

nents. We separate out the weather part as follows:

Let us denote

= w

− h

where x

is the difference between the actual water

level w

and the harmonic forecast h

at the moment

n. Then we can apply a bootstrapping technique to

ﬁnd the next value of x from the water levels of the

preceding n hours. That is, we can predict next hour

difference between water level and harmonic level

= a

+ a

−1

+ . . . + a

−n

and step by step

= a

k−1

+ a

k−2

+ . . . + a

−n

k−n

Now we ﬁnd the prediction for water levels as by

adding the harmonic forecast h

to the forecasted dif-

ference x

= h

+ x

This symbiosis of regression and harmonic analysis

approach to the predictions of water levels proved to

be very effective.

5 MODEL PERFORMANCE

ASSESSMENT

Once water level predictions are developed,

they are evaluated based on a suite of Na-

tional Ocean Service Skill Assessment Statistics.

Error predicted value − observed value

SM series mean

RMSE root mean square error

SD standard deviation

CF(X) central frequency;

% of errors between −X and X

POF(2X) positive outlier frequency

NOF(2X) negative outlier frequency

MDPO(2X) max. duration of positive outlier

MDNO(2X) max. duration of negative outlier

A web-based tool (see Figure 9) was created that

combines harmonic analysis with multivariate sta-

tistical modeling to predict water levels along the

Texas Gulf Coast. Water level predictions, as well

as skill assessment statistics, are dynamically gener-

ated based on a set of user given criteria including

station identiﬁer, dates, number of coefﬁcients (that

REAL TIME WEB AVAILABILITY OF STATISTICAL MODELS FOR WATER LEVELS ALONG THE TEXAS

COASTLINE

221

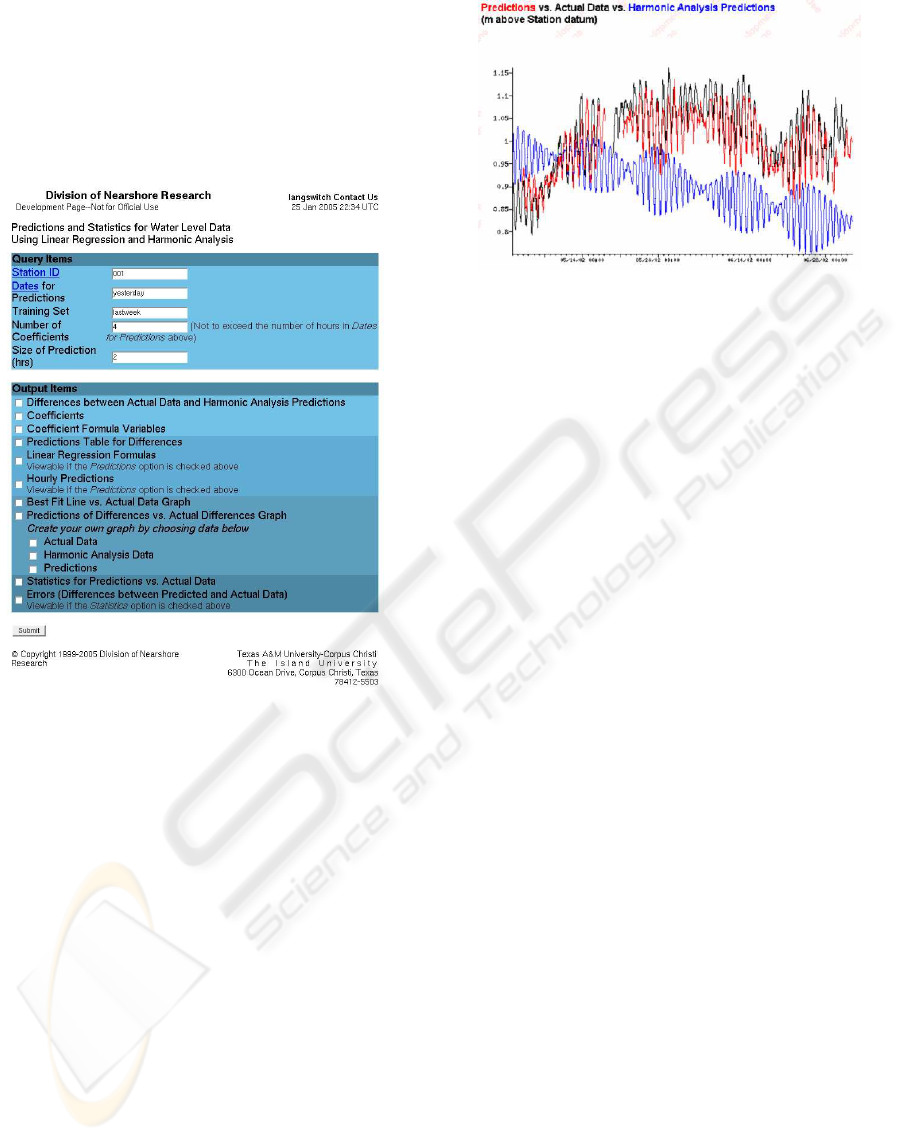
is, the number of hours) of linear regression, and a

prediction range. The programming was done as CGI

scripts in Perl using the Perl Data Language (PDL)

and inputs from the TCOON database. The tool is

available on the web and can be used for any TCOON

station.

Figure 9: Web based tool to generate water level

predictions at the TCOON stations using a symbio-

sis of harmonic forecasts and linear regression. Lo-

cation: http://wip.cbi.tamucc.edu/∼jessica/pharosdb/cgi-

bin/excel/sdiffcoeff.cgi (Development page)

6 MODEL PERFORMANCE

Using the previously described web based tool, fore-

casts were computed for the Packery Channel Station,

near Corpus Christi, Texas. A graphical comparison

between harmonic analysis forecasts, observed water

levels and model predictions is presented in Figure

10. As can be observed in the ﬁgure model fore-

casts result in a substantial improvement over har-

monic analysis. The performance improvement is fur-

ther quantiﬁed using the NOS skill assessment criteria

described above. Here are the National Ocean Service

Skill Assessment Statistics for the given example:

Figure 10: Comparison of Predictions with the Measured

Water for Packery Channel 05/01/02-06/31/02

SM (predicted) 0.996

SM (actual) 0.995

RMSE 0.159

SD 0.159

CF (15 cm) 97.64%

POF (30 cm) 2.35%

NOF (30 cm) 0.00%

MDPO (30 cm) 24

MDNO (30 cm) 0

The advantage of this model is its stability; the

quality of its forecasts are close to the quality of

forecasts obtained with neural networks in (Sadovski

et al., 2003b).

7 FURTHER MODEL

DEVELOPMENT

Apart from being used as a forecast tool, this mod-

eling technique has also been adapted to the problem

of ﬁlling gaps. Gaps in the water level time series

occur due to equipment failure, etc. Figure 11 de-

picts data collected at the Texas State Aquarium sta-

tion with a gap spanning over 24 hours during Janu-

ary 2003. Linear interpolation of the data would not

adequately ﬁll the gap. Forward and backward linear

regression are applied to complete the water level data

sets. Other current work involves further development

of the multivariate statistical model and comparisons

at various locations along the Texas Gulf coast with

harmonic analysis and other forecasting methodolo-

gies such as the persistence and neural network mod-

els (Sadovski et al., 2003a). Future work will general-

ize the forecast capabilities to points along the Texas

coast that lie between TCOON stations.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

222

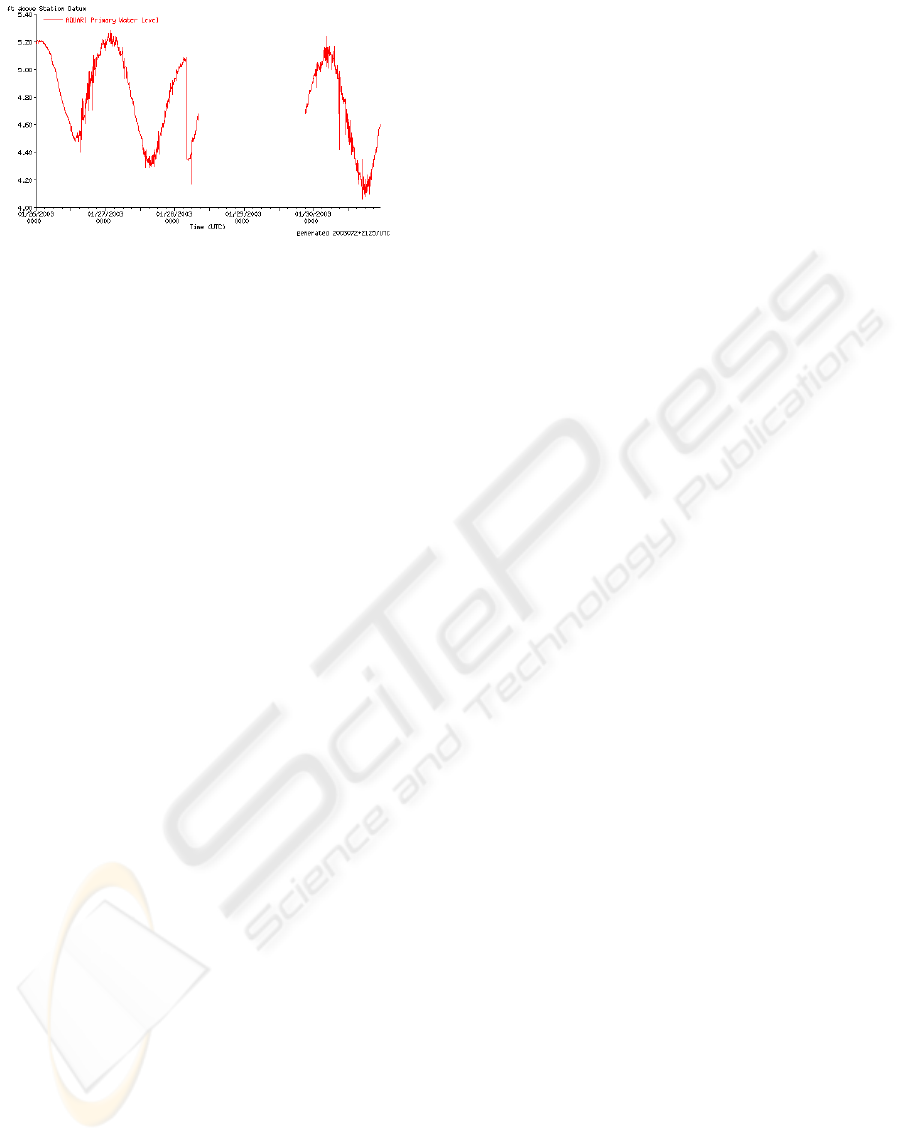
Figure 11: Example of a gap in a water level time series to

be ﬁlled by the forward/backward linear regression method

8 SPONSORS AND RESOURCES

The work presented in this paper is funded in part by

the following federal and state agencies of the USA

- National Aeronautic and Space Agency (NASA

Grant #NCC5-517)

- National Oceanic and Atmospheric Administration

(NOAA)

- Texas General Land Ofﬁce - Coastal Management

Program (CMP)

The following are the web based resources:

- Division of Nearshore Research Website

http://dnr.cbi.tamucc.edu

- TCOON Data Query Page

http://dnr.cbi.tamucc.edu/pquery

- Web-based Predictions Development Page

http://wip.cbi.tamucc.edu/∼jessica/pharosdb

/cgi-bin/excel/sdiffcoeff.cgi

REFERENCES

Cox, D., Tissot, P., , and Michaud, P. (2002). Water

level observations and short term predictions includ-

ing meteorological events for the entrance of Galve-

ston Bay,Texas. Journal of Waterways, Port, Coastal

and Ocean Engineering, 28(1):21–29.

Michaud, P., Jeffress, G., Dannelly, R., and Steidley, C.

(2001). Real time data collection and the Texas

Coastal Ocean Observation Network. In Proc. Inter-

national Measurement and Control (InterMAC).

Sadovski, A. L., C.Steidley, Tissot, P., and Michaud, P.

(2003a). Developing a goodness criteria for tide pre-

dictions based on fuzzy preference ranking. In Devel-

opments in Applied Artiﬁcial Intelligence. Springer.

Sadovski, A. L., Tissot, P. E., Michaud, P., and Steidley, C.

(2003b). Statistical and neural network modeling and

predictions of tides in the shallow waters of the Gulf

of Mexico. In WSEAS Transactions on Systems.

Tissot, P., Cox, D., and Michaud, P. (2002). Forecasting of

storm surges along the Gulf of Mexico. In Proceed-

ings of the Fourth International Symposium on Ocean

Wave Measurement and Analysis (Waves ‘01).

REAL TIME WEB AVAILABILITY OF STATISTICAL MODELS FOR WATER LEVELS ALONG THE TEXAS

COASTLINE

223