TRACKING-CONTROL INVESTIGATION OF TWO X4-FLYERS

K. M. Zemalache, L. Beji and H. Maaref

Universit

e d’Evry - CNRS FRE 2494

Laboratoire Syst

emes Complexes (LSC)

40 rue du Pelvoux,91020 Evry Cedex, France

Keywords:

X4-ﬂyer, dynamical systems, backstepping control, tracking control.

Abstract:

Two models of mini-ﬂying robots with four rotors called X4-ﬂyer presented and studied for the stabilization.

Both cases with and without motion planning are proposed in this paper. The ﬁrst is called inertial model with

axes orientation and the second is called the inertial model without axes orientation. The control algorithm of

the X4-ﬂyer is based on the Lyapunov method and obtained using the backstepping techniques. This enabled

to stabilize the engine in hovering and to generate its trajectory. The system behavior using the proposed

control law is described through numerical simulations.

1 INTRODUCTION

The automatic control of ﬂying machines has at-

tracted the attention of many researches in the past

few years. Generally, the control strategies are based

on simpliﬁed models which have both a minimum

number of states and a minimum number of input.

These reduced models should retain the main features

that must be considered when designing control laws

for real aerial vehicles. The rotorcraft is one the most

complex ﬂying machines. Its complexity is due to

the versatility and manoeuvrability to perform many

types of tasks (Castillo et al., 2004). Very little atten-

tion has been done on the development of aerial ro-

botic platforms (Altug, 2003) (Altug et al., 2003) (Al-

tug et al., 2002) (Hamel et al., 2002) (Zhang, 2000).

Such platforms have considerable commercial poten-

tial for surveillance and inspection roles in dangerous

environments.

Modelling and controlling aerial vehicles (blimps,

mini rotorcraft) are the principal preoccupation of our

laboratory (LSC). In this topic, a mini-UAV is de-

velopped by the LSC-group taking into account in-

dustrial constraints. The aerial ﬂying engine could

not exceed 2kg in mass, a wingspan of 50cm with

a 30mn ﬂying-time (see ﬁgure 1). Within this optic,

it can be held that our system belongs to a family of

mini-UAV. It is an autonomous hovering system, ca-

pable of vertical takeoff, landing, lateral motion and

quasi-stationary (hover or near hover) ﬂight condi-

tions. Compared to helicopters (Altug, 2003) (Altug

et al., 2003) (Altug et al., 2002), the four rotors ro-

torcraft called X4-ﬂyer has some advantages (Hamel

et al., 2002) (Pound et al., 2002): given that two mo-

tors rotate counter clockwise while the other two ro-

tate clockwise, gyroscopic effects and aerodynamic

torques tend, in trimmed ﬂight, to cancel. An X4-ﬂyer

operates as an omnidirectional UAV. Vertical motion

is controlled by collectively increasing or decreasing

the power for all motors. Lateral motion, in x direc-

tion or in y direction, is achieved by differentially

controlling the motors generating a pitching/rolling

motion of the airframe that inclines the collective

thrust (producing horizontal forces) and leads to lat-

eral accelerations.

Several recent work was completed for the design

and control in pilot-less aerial vehicles domain such

that Quadrotor (Altug, 2003) (Altug et al., 2003) (Al-

tug et al., 2002), X4-ﬂyer (Hamel et al., 2002), mesi-

copter (Kroo and Printz, ) and hoverbot (Borenstein,

). Also, related models for controlling the VTOL

aircraft are studied by Hauser and al (Hauser et al.,

1992). A model for the dynamic and conﬁguration

stabilization of quasi-stationary ﬂight conditions of a

four rotors vertical take-off and landing (VTOL) was

studied by Hamel (Hamel et al., 2002) where the dy-

namic motor effects are incorporating and a bound of

perturbing errors was obtained for the coupled sys-

tem. The stabilization problem of a four rotors rotor-

craft is also studied and tested by Castillo (Castillo

M. Zemalache K., Beji L. and Maaref H. (2005).

TRACKING-CONTROL INVESTIGATION OF TWO X4-FLYERS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 16-23

DOI: 10.5220/0001157600160023

 SciTePress

et al., 2004) where the nested saturation algorithm is

used and application of the theory of ﬂat systems by

Beji et al (Beji et al., 2004).

Figure 1: Conceptual form of the four rotors rotorcraft.

In this paper, the backstepping controllers and mo-

tion planning are combined to stabilize the helicopter

by using the point to point steering stabilization. Af-

ter having presented the study of modeling and the

description of the conﬁguration in the second section.

Third section describes the dynamics of the system

which treats the two models with and without axes

orientation. Backstepping controllers is described for

two models of the X4-ﬂyer in the fourth section. A

strategy to solve the tracking problem through point

to point steering is shown in the ﬁfth section. In the

sixth section simulation results are introduced for two

models. Finally, conclusion and future work are given

in the last section.

2 CONFIGURATION

DESCRIPTION AND

MODELLING

Unlike regular helicopters that have variable pitch an-

gles, an engine has ﬁxed pitch angle rotors and the

rotor speeds are controlled to produce the desired lift

forces. Basic motions of the four rotors rotorcraft

can described using the ﬁgure 2. Vertical motion is

controlled by collectively increasing or decreasing the

power for all motors. Lateral motion, in x direction or

in y direction, is not achieved by differentially con-

trolling the motors generating a pitching/rolling mo-

tion of the airframe that inclines the collective thrust

(producing horizontal forces) and leads to lateral ac-

celerations (case of the X4-ﬂyer). But, two engines

of direction are used to permute between the x and y

motion.

We consider a local reference airframe ℜ

{G, E

, E

} attached to the mass center G of the

vehicle. The mass center is located at the intersec-

tion of the two rigid bars, each of which supports two

motors. Equipments (controller cartes, sensors, etc.)

Figure 2: 3D X4-ﬂyer model.

onboard are placed not far from G. The inertial frame

is denoted by ℜ

= {O, E

, E

}. A body ﬁxed

frame is assumed to be at the center of gravity of the

X4-ﬂyer, where the z axis is pointing upwards. This

body axis is related to the inertial frame by a position

vector (x, y, z) and 3 Euler angles (θ, φ, ψ) represent-

ing pitch, roll and yaw respectively. A Euler angle

representation given in (1) has been chosen.

R =

−S

− S

+ C

+ S

− C

(1)

Where C

and S

represent cos θ and sin θ repec-

tively.

Each rotor produces moments as well as vertical

forces. These moments have been experimentally ob-

served to be linearly dependent on the forces for low

speeds. There are four/ﬁve input forces and six out-

put states (x, y, z, θ, φ, ψ) therefore the X4-ﬂyer is an

under-actuated system. The rotation direction of two

of the rotors are clockwise while the other two are

counterclockwise, in order to balance the moments

and produce yaw motions as needed.

In the present work, two X4-ﬂyer models are pre-

sented, the ﬁrst is called the inertial model with axes

orientation, the second one is the inertial model with-

out axes orientation. For the model without axes ori-

entation, the rotors 2 and 4 are actuated in clock-

wise direction, the remain rotors, the rotors 1 and 3

are in the contrary actuated in the inverse direction

in order to guarantee total balance in yaw (ﬁgure 4).

The main feature of the presented X4-ﬂyer (called the

XSF) in comparison with the existing quadrirotors, is

the swiveling of the actuators supports 1 and 3 around

the axis of pitching (angles ξ

and ξ

). This swiveling

ensures either the horizontal rectilinear motion or the

TRACKING-CONTROL INVESTIGATION OF TWO X4-FLYERS

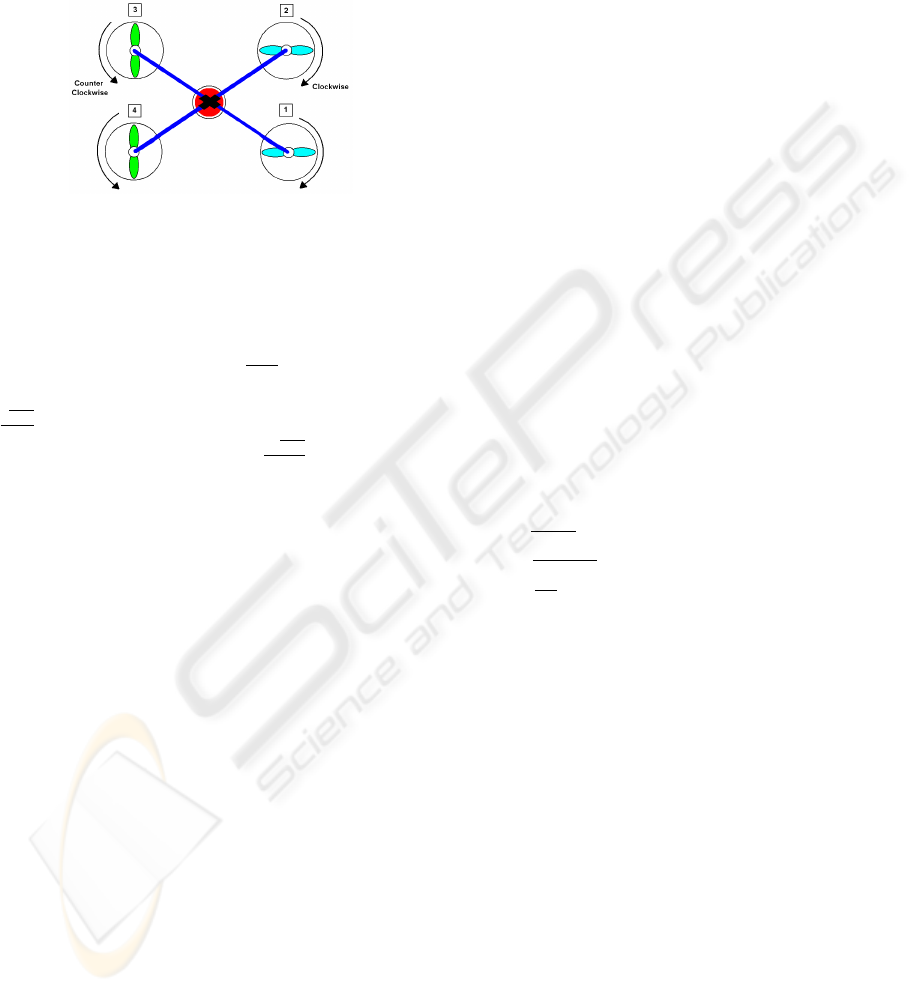
rotational movement around the yaw axis or a combi-

nation of these two movements which gives the turn

(see the ﬁgure 3), as well as the direction of rotation

of the rotors implies that rotors 1 and 2 turn clockwise

and rotors 3 and 4 turn in the contrary direction of the

needles of a watch.

Figure 3: Rotor rotations with canceled yaw motions.

3 MOTION DYNAMIC

We consider the translation motion of ℜ

with re-

spect to (wrt) ℜ

. The position of the center of

mass wrt ℜ

is deﬁned by

OG = (x y z)

, its

time derivative gives the velocity wrt to ℜ

such that

= ( ˙x ˙y ˙z)

, while the second time derivative

permits to get the acceleration

= (¨x ¨y ¨z)

In the following, the model with axes orientation is

described, then the model without axes orientation is

given.

3.1 Dynamic Motion of the Model

with Axes Orientation

Currently, the model is a simpliﬁed one’s. The con-

straints and the gyroscopic torques are neglected. The

aim is to control the engine vertically (z) axis and hor-

izontally according to x and y axis. The dynamics of

the vehicle, represented on ﬁgure 2, is modelled by

the system of equations (2), (Beji et al., 2005).

m¨x = S

− S

m¨y = (S

+ C

) u

+ C

m¨z = (S

− C

) u

+ C

− mg

(2)

Where m is the total mass of the vehicle. The vec-

tor u

and u

combines the principal non conservative

forces applied to the engine airframe including forces

generated by the motors and drag terms. Drag forces

and gyroscopic due to motors effects will be not con-

sidered in this work. The lift (collective) force u

and

the direction input u

are such that

= f

´e

+ f

´e

+ f

(3)

with f

= k

, k

> 0 is a given constant and ω

is the angular speed resulting of motor i. Let

´e

ℜ

; ´e

ℜ

= e

ℜ

(4)

Then we deduce:

= f

+ f

= f

+ f

(5)

and ξ

are the two internal degree of freedom of

rotors 1 and 3, respectively. These variables are con-

trolled by dc-motors and bounded −20

≤ ξ

, ξ

≤

+20

. e

and e

are the unit vectors along E

which

imply that rotors 2 and 3 are identical of that of a clas-

sical Quadrotor (not directional).

3.2 Rotational Motion of the Model

with Axes Orientation

The rotational motion of the X4 bidirectional ﬂyer

will be deﬁned wrt to the local frame but ex-

pressed in the inertial frame. According to Classi-

cal Mechanics, and knowing the inertia matrix I

diag (I

, I

) at the centre of the mass.

θ =

(τ

+ I

θ)

φ =

(τ

+ I

φ˙

+ I

φ)

ψ =

(6)

With the three inputs in torque

= l (f

− f

)

= l (f

− f

)

= l (f

− f

)

(7)

where l is the distance from G to the rotor i. The

equality from (6) is ensured, meaning that

¨η = Π

(η)

−1

[τ −

(η) ˙η] (8)

With τ = (τ

, τ

)

as an auxiliary inputs.

And

(η) =

0 0

0 I

0 0 I

(9)

As a ﬁrst step, the model given above can be

input/output linearized by the following decoupling

feedback laws

= −I

θ + I

˜τ

= −I

− I

φ + I

˜τ

= I

˜τ

(10)

ICINCO 2005 - ROBOTICS AND AUTOMATION

and the decoupled dynamic model of rotation can

be written as

¨η = ˜τ (11)

with ˜τ = (˜τ

˜τ

)

Using the system of equations (2) and (11), the dy-

namic of the system is deﬁned by

m¨x = S

− S

m¨y = (S

+ C

) u

+ C

m¨z = (S

− C

) u

+ C

− mg

θ = ˜τ

;

φ = ˜τ

;

ψ = ˜τ

(12)

3.3 Dynamic Motion of the Model

without Axes Orientation

We follows the same steps as the model with axes ori-

entation and ﬁnally we ﬁnds for the dynamics of the

X4-ﬂyer without the axes orientation:

m¨x = −S

m¨y = C

m¨z = C

− mg

(13)

3.4 Rotational Motion of the Model

without Axes Orientation

The three inputs in torque are given by:

= l (f

− f

)

= l (f

− f

)

= lk (f

− f

+ f

− f

)

(14)

The vertical controller is: u

= f

+ f

Using the translational and rotational motions (13)

and (14), equations of the dynamic are detailed by

m¨x = −S

m¨y = C

m¨z = C

− mg

θ = ˜τ

;

φ = ˜τ

;

ψ = ˜τ

(15)

Remark: As shown in the system (2), the three inputs

torque see the equation (7), the yaw τ

is equal to

zero if we take ξ

= ξ

= 0. Then, with the proposed

sense of rotations (see ﬁgure 3), we can not generate

yaw motions if rotors 1 and 3 are not oriented. With

= ξ

= 0, to obtain yaw motions, the rotor sense

of rotations is identical of that of the Quadrotor.

Then rotors 1 and 3 are with the same sense of rota-

tions, while rotors 2 and 4 are in opposite sense (see

ﬁgure 4).

With or without axes orientation, the rotational part

can be easily linearized with static feedback control

laws. Then, we get

θ = u

φ = u

ψ = u

(16)

Figure 4: Rotor rotations with yaw motions.

with

(τ

+ I

θ)

(τ

+ I

φ)

(17)

4 BACKSTEPPING BASED

CONTROLLER

Backstepping controllers are especially useful when

some states are controlled through other states. As

it was observed in the previous section, in order to

control the x and y motion of the X4-ﬂyer, tilt an-

gles need to be controlled. Therefore a backstepping

controller has been developed in this section. Similar

ideas of using backstepping with visual serving have

been developed for a traditional helicopter by Hamel

and Mahony (Hamel and Mahony, 2000). As well as

the backstepping controllers was applied for Quadro-

tor by Altug et al (Altug, 2003) (Altug et al., 2003)

(Altug et al., 2002).

4.1 ”Backstepping” Application to

the Model without Axes

Orientation

4.1.1 Altitude and yaw control

The altitude and the yaw on the other hand, can be

controlled by a PD controller. With through the equa-

tion of the following movement (z).

m¨z = C

− mg (18)

The control of the vertical position (altitude) can be

obtained considering the following control input

= m



g + ¨z

− k

( ˙z − ˙z

) − k

(z − z

)



(19)

with

¨z = ¨z

− k

( ˙z − ˙z

) − k

(z − z

) (20)

TRACKING-CONTROL INVESTIGATION OF TWO X4-FLYERS

is the desired altitude. The yaw attitude can be

stabilized to a desired value with the following track-

ing feedback control

− k

(

ψ −

) − k

(ψ − ψ

) (21)

where k

, k

are the coefﬁcients of stable

polynomial.

4.1.2 Roll control (φ, y)

First we notice that motion in the y direction can

be controlled through the changes of the roll angle.

These variables are related by the cascade system



m¨y = C

φ = u

(22)

This leads to a backstepping controller for y − φ

control given by

(5y + 10 ˙y + u

θ,φ

) (23)

where

θ,φ



+ 4

φC

−

θS

θC

−

φC



(24)

4.1.3 Pitch control (θ, x)

To develop a controller for motion along the x axis,

similar analysis is needed. The equation of motion of

the X4-ﬂyer on x is given as



m¨x = −S

θ = u

(25)

This leads to a backstepping controller for x − θ

control given by

(−5x − 10 ˙x + u

) (26)

where

= 9S

+ 4

θC

−

(27)

4.2 Model with Axes Orientation

4.2.1 Control input for (z − y) motions

We propose to control motion along y and z direc-

tions through u

and u

, respectively. So we have the

proposition (28).



¨y

¨z







−





(28)

where

H =



+ C

− C



(29)

For the given conditions in ψ and θ , the 2 by 2

matrix (29) is invertible. Then a nonlinear decou-

pling feedback permits to write the following decou-

pled linear dynamics

¨y = ν

¨z = ν

(30)

Then we can deduce from (30) the linear controller

= ¨y

− k

( ˙y − ˙y

) − k

(y − y

)

= ¨z

− k

( ˙z − ˙z

) − k

(z − z

)

(31)

With the k

and k

are the coefﬁcients of a polyno-

mial of Hurwitz

Proposition: Consider

(ψ, θ) ∈

−

(32)

with the controllers (33) and (34)

(m¨y) −

(m (¨z + g)) (33)

−S

(m¨y) +

(m (¨z + g))

(34)

The dynamic of y and z are linearly decoupled and

exponentially-asymptotically stable with the appro-

priate choice of the gain controller parameters.

4.2.2 Control input for the x motion

To control the movement along the x axis, the back-

stepping controller is used. The noted controller x −θ

is given by the equation (35):



m¨x = S

− S

θ = u

(35)

One supposes it exists a time T

such that ∀t∈

, T

, u

> 0, then the dynamic of x is decou-

pled under the following controller

+ u

(−5x − 10 ˙x + u

+ u

θ,ψ

)

(36)

where

= 9S

+ 4

θC

−

(37)

and

θ,ψ

+ 4

θC

−

ψS

θC

−

ψC

(38)

ICINCO 2005 - ROBOTICS AND AUTOMATION

5 TRAJECTORY GENERATION

AND POINT TO POINT

STEERING

Due to the structure limit of the X4-ﬂyer, motion can

be asserted only in straight line along the x, y and z

directions. In our case, that is sufﬁcient to navigate in

a region. Otherwise, an other version of the engine is

under study by the group. The version ﬂyer is to make

easy manoeuvres in corners with arc of circle. In the

following, we solve the tracking problem as point to

point steering one over a ﬁnite interval of time. Then

we take each ending point with its ﬁnal time as a new

starting point.

0 2 4 6 8

z−ref (m)

time (s)

10 15 20 25

time (s)

x−ref (m)

20 25 30 35

y−ref (m)

time (s)

x−displacement

y−displacement

z−displacement

Figure 5: Motion planning with h

= 10m.

Figure 5 illustrate the reference trajectory along the

x, y and z directions. As we see, the X4-ﬂyer will ﬂy

in the z direction followed by the x − motion and the

y−motion. The reference trajectory is parameterized

(t) = h

+ (T

− t)

(39)

where h

is the desired altitude and (T

) the ﬁnal

time. In order to solve the point to point steering con-

trol, the end point of the trajectory (39) can be adopted

as initial point to move along x, then we have

(t) = h

(t − T

)

(t − T

)

+ (T

− (t − T

))

(40)

As soon as for y

(t)

(t) = h

(t − T

)

(t − T

)

+ (T

− (t − T

))

(41)

The constraints to perform these trajectories are

such that











(0) = x

) = y

) = 0

) = x

) = y

) = h

˙z

(0) = ˙x

) = ˙y

) = 0

˙z

) = ˙x

) = ˙y

) = 0

¨z

(0) = ¨x

) = ¨y

) = 0

¨z

) = ¨x

) = ¨y

) = 0

(42)

Minimizing the time of displacement implies that

the X4-ﬂyer accelerates at the beginning and deceler-

ates at the arrival.

6 SIMULATION RESULTS

Two engine models were studied and controlled us-

ing the backstepping technique which (a) present the

model with axes orientation and (b) the model with-

out axes orientation.

0 20 40

−0.2

0.2

z−erreur (m)

0 20 40

−1

x−erreur (m)

0 20 40

−0.05

0.05

y−erreur (m)

0 20 40

−0.2

0.2

z−erreur (m)

0 20 40

−1

x−erreur (m)

0 20 40

−1

y−erreur (m)

time (s)

(a)

(b)

Figure 6: Displacement errors: (a) with axes orientation -

(b) without axes orientation.

Figure 6 show displacement errors according to all

the directions for the models with and without axes

orientations. It is noticed that the error thus tends to

zero towards the desired positions.

Figure 7, we notices that the angles θ and φ control

the engine for displacements along the axes x and y.

These angles tend to zero value. It is also shown in

ﬁgure 8(a) that we can stabilize the system to make a

following movement by the swivelling of the engine

actuators 1 and 3.

According to the ﬁgure 8, which represent our ve-

hicle input, we remark that the input u

= mg at the

equilibrium state is always veriﬁed. The inputs u

and u

tend to zero after having carried out the de-

sired orientation of the vehicle. These Figure 8 also

show the effectiveness of the used controllers laws.

TRACKING-CONTROL INVESTIGATION OF TWO X4-FLYERS

0 20 40

−0.1

−0.05

0.05

0.1

angle phi (rad)

0 20 40

−0.2

−0.1

0.1

0.2

angle theta (rad)

(a)

(b)

0 20 40

−0.1

−0.05

0.05

0.1

angle phi (rad)

0 20 40

−0.2

−0.1

0.1

0.2

angle theta (rad)

time (s)

Figure 7: The pitch θ and the roll φ: (a) with axes orienta-

tion - (b) without axes orientation.

0 20 40

u3 (N)

0 20 40

−0.5

0.5

u4 (Nm)

0 20 40

−2

u2 (N)

0 20 40

u3 (N)

0 20 40

−0.5

0.5

u4 (Nm)

0 20 40

−0.1

0.1

u5 (Nm)

time (s)

(a)

(b)

Figure 8: Inputs u

, u

and u

for the xyz displace-

ment: (a) with axes orientation - (b) without axes orienta-

tion.

0 5 10

z,z

(m)

0 5 10

x,x

(m)

0 5 10

y,y

(m)

0 5 10

z,z

(m)

0 5 10

x,x

(m)

0 5 10

y,y

(m)

time (s)

(a)

(b)

Figure 9: Without motion planning with h

= 5m: (a) with

axes orientation - (b) without axes orientation.

0 5 10

z−erreur (m)

0 5 10

x−erreur (m)

0 5 10

y−erreur (m)

0 5 10

z−erreur (m)

0 5 10

x−erreur (m)

0 5 10

y−erreur (m)

time (s)

(a)

(b)

Figure 10: Tracking errors without motion planning (z

= y

= 5m): (a) with axes orientation - (b) without

axes orientation.

Figures 9,10,11 and 12, show the system without

motion planning. Motion in different directions z, x

and y is also tested and shown by ﬁgure 9. In addition

we show that the behavior of errors, given by ﬁgure

10 is veriﬁed. At the equilibrium, attitudes of θ and φ

are equal to zero (ﬁgure 11).

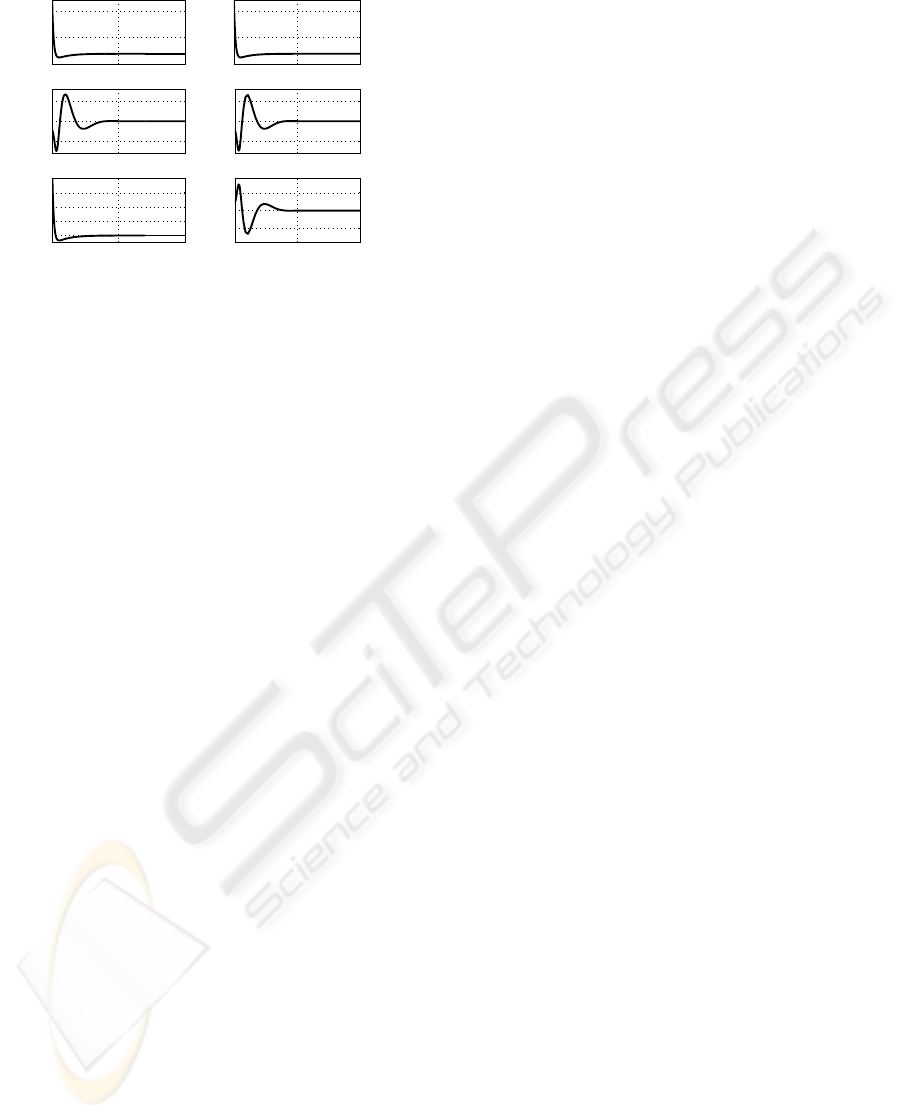
Without motion planning, the amplitude of controllers

is important (ﬁgure 12) and a maximum of energy is

asserted which is requested for ﬂying vehicles.

0 5 10

−0.2

−0.1

0.1

0.2

angle phi (rad)

0 5 10

−0.2

−0.1

0.1

0.2

angle theta (rad)

(a)

(b)

0 5 10

−0.2

−0.1

0.1

0.2

angle phi (rad)

0 5 10

−0.2

−0.1

0.1

0.2

angle theta (rad)

time (s)

Figure 11: The pitch θ and the roll φ for the vehicle without

motion planning: (a) with axes orientation - (b) without axes

orientation.

7 CONCLUSION

The study of the stabilization with and without a pre-

deﬁned trajectory of the mini-ﬂying robot with four

rotors (X4-ﬂyer) was discussed in this paper. The

importance of the trajectory generation and its con-

sequences with respect to amplitude of the used con-

troller, was highlited. With the proposed motion plan-

ICINCO 2005 - ROBOTICS AND AUTOMATION

0 5 10

100

u3 (N)

0 5 10

−0.5

0.5

u4 (Nm)

0 5 10

u2 (N)

0 5 10

100

u3 (N)

0 5 10

−0.5

0.5

u4 (Nm)

0 5 10

−0.5

0.5

u5 (Nm)

time (s)

(a)

(b)

Figure 12: Inputs u

, u

and u

for the vehicle without

motion planning: (a) with axes orientation - (b) without axes

orientation.

ning, actuator saturations can be overcomed. Con-

sequently, economy in energy of batteries can be as-

serted during the ﬂy. The backstepping technique was

successfully applied and enabled us to design control

algorithms ensuring the vehicle displacement from an

initial position to a desired position. The backstep-

ping approach used requires the well knowledge of

the system model and parameters. Future work is

to develop the fuzzy controller based algorithm (does

not require the good knowledge of the model) (Maaref

and Barret, 2001) and to make the comparison of both

controllers. A realization of a control system based on

engine sensors information is envisaged.

REFERENCES

Altug, E. (2003). Vision based control of unmanned aerial

vehicles with applications to an autonomous four ro-

tor helicopter, quadrotor. PhD thesis, faculties of the

university of Pennsylvania.

Altug, E., Ostrowski, J. P., and Mahony, R. (2002). Control

of a quadrotor helicopter using visual feedback. In

Proceeding of the IEEE International Conference on

Robotics and Automation, Washington D.C.

Altug, E., Ostrowski, J. P., and Taylor, C. (2003). Quadrotor

control using dual visual feedback. In Proceeding of

the IEEE International Conference on Robotics and

Automation, Taipei, Taiwan.

Beji, L., Abichou, A., and Slim, R. (2004). Stabilization

with motion planning of a four rotor mini-rotorcraft

for terrain missions. International Conference on Sys-

tems Design and Application, ISDA, Budapest, Hun-

gary.

Beji, L., Abichou, A., and Zemalache, K. M. (2005).

Smooth control of an x4 bidirectional rotors ﬂying ro-

bots. Fifth International Workshop on Robot Motion

and Control, Dymaczewo, Poland.

Borenstein, J. Hoverbot project. University of Michi-

gin, www-personal.engin.umich.edu/ johannb/ Hover-

bot.htm.

Castillo, P., Dzul, A., and Lozano, R. (2004). Real-time sta-

bilization and tracking of a four rotor mini-rotorcraft.

IEEE Transactions on control Systems Technology.

Hamel, T. and Mahony, R. (2000). Visual serving of a class

of under-actuated dynamic rigid-body systems. Pro-

ceeding of the 39th IEEE Conference on decision and

control.

Hamel, T., Mahony, R., Lozano, R., and Ostrowski, J. P.

(2002). Dynamic modelling and conﬁguration stabi-

lization for an x4-ﬂyer. in IFAC 15th World Congress

on Automatic Control, Barcelona, Spain.

Hauser, J., Sastry, S., and Meyer, G. (1992). Nonlinear con-

trol design for slightly non-minimum phase systems:

Application to v/stol aircraft. Automatica.

Kroo, I. and Printz, F. Mesicopter project. Stanford Univer-

sity, http://aero.stanford.edu/ Mesicopter.

Maaref, H. and Barret, C. (2001). Progressive optimiza-

tion of a fuzzy inference system. IFSA-NAFIPS’2001,

Vancouver.

Pound, P., Mahony, R., Hynes, P., and Roberts, J. (2002).

Design of a four rotor aerial robot. Proceeding of

the Australasian Conference on Robotics and Automa-

tion, Auckland.

Zhang, H. (2000). Motion control for dynamic mobile ro-

bots. PhD thesis, faculties of the university of Penn-

sylvania.

TRACKING-CONTROL INVESTIGATION OF TWO X4-FLYERS