INVARIANT SIGNAL RECOGNITION IN NOISE ENVIROMENT

Riad Taha Al-Kasasbeh

Faculty of Engineering Technology, Al-Balqa Applied University, Amman, Jordan

Keywords: signal/noise, speech recognition, invariant signal recognition.

Abstract: Recognition of signals is considered at the presence of noise. The problem is actual for the speech signals

recognition, acoustic diagnostics of mechanisms. The model of recognized signal contains a priori unknown

parameter - the relation a signal / noise. For considered model the approach to construction of the signal

description, which is invariant to a level of the noise is offered. Efficiency of invariant signals recognition is

analyzed.

1 INTRODUCTION

The task of recognition of random noise signals with

reference to such tasks as speech recognition

(S1ozokai et al., 1998) (Schalkoff, 1992), technical

diagnostics of mechanisms on their noise, processing

of the biomedical data is considered.

In real conditions of application of recognizing

devices for such tasks it is necessary to allow the

fact, that on an input of the recognizing device the

signal is the sum of a temporary useful signal and

one or several disturbance acts. The noncorrelation

of a useful signal and disturbances among

themselves is supposed. As is known, many tasks of

recognition of random signals effectively are solved

by transition in spectral area. Therefore in the

spectral form representation of a signal, it is possible

to write

),()()(

ω+ω=ω

∑

SSS

(1)

Where - spectrum of a signal on an input of

the classifier, - spectrum of a useful signal,

- spectrum i-th noise disturbance, k – number of

noise. Further passing to the description of a

spectrum in the vector form as countings on the

given set of frequencies

, ω

, …….., ω

and

entering concept of the normalized vectors of the

spectral description of a signal and noise ,

expression (1) it is possible to write as

∑

λ+λ=

niC

xxS

(2)

Where

and

- the coefficients defining

accordingly power of a signal and disturbances

appropriate. Thus the ratio

is the ratio signal

/ noise for i-th noise.. In case power of a classified

signal does not carry the information on the class of

the recognized object, parameters

and

can be

considered as hampering parameters.

Since signal distortion parameters (in particular

the ratio signal / noise) are unknown, and distortions

can reach significant values, there is impossible a

correct recognition of signals with the help of the

classifier is trained with standard signals, or on

the signals subjected to distortions with parameters,

distinguished from what take place actually at the

moment of recognition. Various approaches to

solution of the considered task are known. The most

widespread is the method of spectral subtraction of

disturbances and its various modifications (Glunder,

1991) (Pattern Recognition and Image Analysis,

2003). A disadvantage of this approach is necessity

of knowledge of the ratio signal / noise or obtaining

of its estimation. In some cases to receive this

estimation it is not possible and accordingly the ratio

signal noise appears as hampering parameter to the

task of recognition. In such situation natural way is

initial creation of the new system of features, wich

are invariants (Ben-Arie and Wang, 2002) (Flusser

and Suk, 1993) (Glunder, 1991) concerning effect of

hampering parameters is represented. Construction

of the decision rules is made already at the following

Taha Al-Kasasbeh R. (2005).

INVARIANT SIGNAL RECOGNITION IN NOISE ENVIROMENT.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 79-83

DOI: 10.5220/0001157900790083

 SciTePress

stage, and the class of decision rules that can be used

for classification, beforehand to nothing is limited.

2 CREATION OF INVARIANT

DESCRIPTIONS OF A SIGNAL

AT RECOGNITION ON A

BACKGROUND OF

DISTURBANCES WITH

UNKNOWN POWER

Let's consider a case when on an input of recognition

device the signal is, combined with one (k=1)

additive disturbance. And powers of a useful signal

and disturbance are unknown, is equal as the ratio

signal / noise q is not known also. Is known sort of

the normalized spectrum of power of the noise

disturbance, described as vector

of dimension d

. Then the spectral vector of power of a recognized

signal

can be written as

=С

+С

(3)

Where

- spectral vector of normalized useful

signal, С

,С

– the unknown coefficients depending

on powers of a useful signal and disturbance.

If the signal on an input of the classifier is

exposed to normalization on power it is easy to

show, that coefficients С

and С

depend only on the

ratio signal / noise. Taking into account model of a

signal (3), we shall enter in space the initial features

X set of transformations

G= {g: g

}, (4)

< , - <∞ ∞

< . ∞

Is simple enough to show that these transformations

is algebraic group of transformations, caused by two

subgroups

= {g

: g

}, 0<

< , ∞

= {g

: g

= +

}, - <∞

∞

Construction of the invariant description of a signal

in the indicated setting is reduced to finding

maximum invariant (MI) of transformations group

G (Leman, 1959). For construction MI concerning

group of transformations G the stage-by-stage

method of construction MI offered by Leman

(Leman, 1959) is used. In the beginning it is defined

MI concerning subgroup G

. It is shown by usage

(Geppener and Ekalo, 2002), that it is linear

transformations

= А

, (5)

Where the matrix A by dimensions (d-1) *d defines

transition in new space Y of features with,

dimension d-1 , and satisfies to a condition

=0 (6)

Geometrical interpretation of invariant

transformations (5) consists that we select a new

coordinate system, one of w ich axes coincides with

a direction of a vector

. In the further this

coordinate is discarded. Thus, is constructed the

matrix of transformations A , which rows are the

vectors of new axes of coordinates except

. For

construction of new basis the procedure of

orthonormalization by Gramm-Shmidt , in

particular, can be used.

Effect of a subgroup of

induces a subgroup

of the transformations in space Y defined as

}.:{

yyggG

== (7)

MI is relative to (7) is usual normalization and can

appear as

(8)

where

- norm of vector

, defined, in

particular, as

∑

According to the theorem of a stage-by-stage

method of construction MI (Leman, 1959), we

receive an ending expression for MI concerning

group G .

(9)

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

3 EXPERIMENTS

For the experimental research of recognition under

the condition of disturbance three etalon

disturbances, used for the noise-protected classifier

training, were generated. During the experiment

distortion of signals was modeled by the disturbance

with the given signal to noise ratio q. In the process

of training a disturbance with fixed spectrum was

used, and for recognition a fluctuation of the

disturbance was modeled defined by factor K

, that

shows the ratio of the mean square deviation of the

disturbance vector to its mean value. Modeling of

two classes of signals for identified objects was

fulfilled. Signals were presented by spectral

description vectors with dimension 50, number of

vectors for each class was equal to 250.

Fig.1 shows the averaged spectra of the generated

signals, when Fig.2 shows the etalon disturbances.

Experiments were done using the training algorithm

based on the Fisher discriminant (Lockwood and

Boudy, 1992) with the use of non-invariant features

in the form of countings of spectra for two classes of

model signals, and the invariant features for three

types of disturbances, correspondingly.

Figure 1: Averaged spectral description.

Figure 2: Spectra of etalon disturbances used of classes in

the experiment

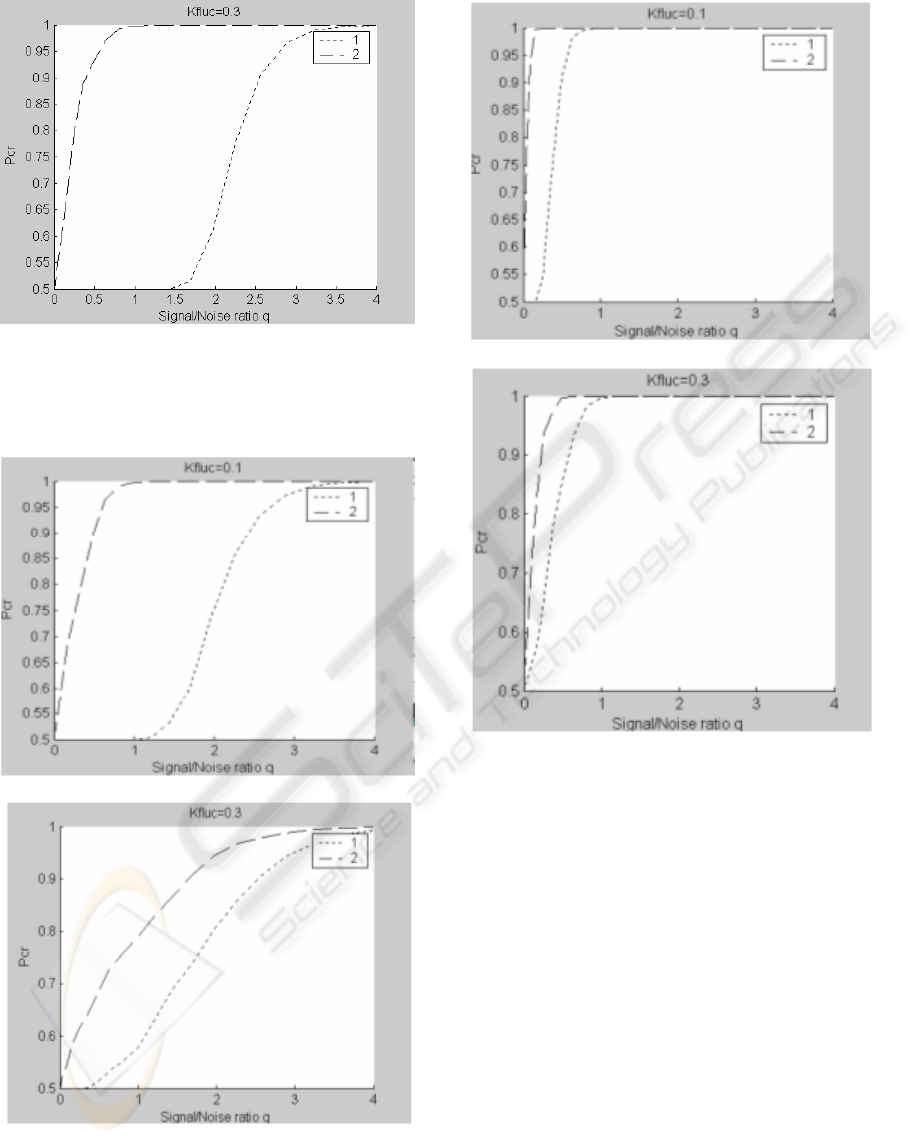
Figures 3-5 show the dependence of the estimation

of correct identification probability P

The signal/noise ratio q. Fig.3 shows the results of

the identification experiments with the first type of

disturbance (in all figures curve 1 corresponds to the

use of non-invariant features, while curve 2

corresponds to the identification with invariant

features. Fig.4 shows experimental results of

identification modeling, made at the same conditions

as in the previous experiments, but for the

disturbance type 2, and Fig.5 shows the

experimental results for the disturbance type 3,

correspondingly.

INVARIANT SIGNAL RECOGNITION IN NOISE ENVIROMENT

Figure 3: Experiment with a model signal with a

disturbance type 1.

a) K

=0.1 , b) K

=0.3

а:

Figure 4: Experiment on the model signal with the

disturbance type 2.

а) K

=0.1 , b) K

=0.3

Figure 5: Experiment on the model signal with the

disturbance type 3.

а) Kfl=0.1 , b) Kfl=0.3

4 CONCLUSIONS

The results of the experiments can be formulated as

follows.

Identification with the Fisher classifier:

for the given sample of signals under the

influence of the disturbance type 1,

The obvious advantage of the noise-protected

classifier based on invariant features is discovered,

together with the deteriorating quality of

identification at the increased fluctuation of the

disturbance.(Fig.3).

Under the influence of disturbances type 2

“noise-protected” dependence is better than non-

protected, but is worse than the dependence with the

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

disturbance type 1 under the same circumstances.

(Fig.4).

under the influence of disturbances type 3 one

can fix the least difference between the noise-

protected dependence and the non-protected one

(Fig.5), but it should be stated that the identification

quality is sufficiently good for both cases even at

small signal/noise ratio, that is the disturbance of

that type is sufficiently “good” for identification.

In addition, similar experiments were done using

perceptron algorithm of identification. As a whole,

the identification results with invariant features for

that algorithm were slightly worse (5-10%)

compared with the Fisher classifier, but the

difference in the identification quality with the

original features was rather big.

Thus, in most cases the investigated method of

invariant identification of signals under the

influence of disturbances gives practically

acceptable results. Nevertheless one should take into

account the fact that under the influence of the

disturbances of certain types the identification

results can be unsatisfactory, so the additional

research in the field is necessary.

REFERENCES

S1ozokai M., Nakamura S., Shicado K. Robust 1998 Car

Recognition in Car Enviroment. ProcICASSP, pp.

269-272.

Ben-Arie J., Wang Z. 2002 Shape Description And

Invariant Recognition Employing Connectionist,

International Journal of Pattern Recognition and

Artificial Intelligence,v. 16, N. 1, 69-83.

Flusser J, Suk T., 1993, Pattern Recognition by Affine

Moment Invariants// Pattern Recognition, v.26, N. 1,

p.167-174.

Glunder H., 1991, Pattern Properties, Invariances, and

Classification, in Vision and Visual

Dysfunction//Pattern Recognition by Man and

Machine, MacMillan Press, p.69-82.

Leman E.L. , 1959, Testing Statistical Hypothesis. Willey

, New York.

Geppener V.V., Ekalo S.A.,2002, Invariant Signal

Recognition in the Presence of Noise //

Pattern Recognition and Image Analysis, 2003, Vol. 13,

No. 2,pp. 266–269

Lockwood P., Boudy J, 1992, Experiments with a

nonlinear spectral subtractor , hidden markov models

and the projection, for robust speech recognition in

cars. Speech Communication, v. 11, pp. 215-228.

R. Schalkoff. , 1992, Pattern Recognition. Statistical,

Structural, and Neural Approaches. John Wiley &

Sons, Inc.

Berouti N., Schwartz R., Makhoul J., 1979 Enhancement

of speech corrupted by acoustic noise. In Proc. Int.

Conf. on Acoustics, Speech and Signal Processing , p.

208-211

INVARIANT SIGNAL RECOGNITION IN NOISE ENVIROMENT