
A NOVEL REPRESENTATION AND ALGORITHMS
FOR (QUASI) STABLE MARRIAGES
B. Y. Zavidovique
Institut d’Electronique Fondamentale, Universit
´
e Paris 11
B
ˆ
atiment 220 - 91405 Orsay Cedex
N. Suvonvorn
Institut d’Electronique Fondamentale, Universit
´
e Paris 11
B
ˆ
atiment 220 - 91405 Orsay Cedex
Guna S. Seetharaman
Air Force Institute of Technology
AFIT/ENG 2950 P Street Wright Patterson AFB OH 45433-7765
Keywords:
stable marriages, matching algorithms.
Abstract:
In this paper, we propose ”stable marriages” algorithms based on a novel representation called marriage table.
After explaining how properties as global satisfaction, sex equality and stability show in the representation,
we define 3 algorithms corresponding to 3 different scans of the marriage table to meet progressively all
constraints. The performance is evaluated in front of the population size for 200 instances in each case.
That supports qualitative statistic analysis. Two matching examples in image processing are displayed for
illustration.
1 INTRODUCTION
The problem of stable marriage was first studied by
Gale and Shapley (Gale and Shapley, 1962). In this
problem, two finite sub-sets M and W of two re-
spective populations, say men and women, have to
match. Assume n is the number of elements, M =
{m
1
, m
2
, ..., m
n
} and W = {w
1
, w
2
, ..., w
n
}. Each
element x creates its preference list l(x) i.e. it sorts
all members of the opposite sex from most to less pre-
ferred. A matching M is a one to one correspondence
between men and women. If (m, w) is a matched pair
in M , we note M(m) = w and M(w) = m and
ρ
m
is the rank of m in the list of w (resp. ρ
w
the
rank of w in the list of m) . Man m and woman
w form a blocking pair if (m, w) is not in M but
m prefers w to M(m) and w prefers m to M(w).
If there is no blocking pair, then the matching M is
stable (Abeledo and Rothblum, 1995), (Diamantoudi
et al., 2004). Gale and Shapley proved that there is
always at least one stable matching M whichever the
instance {M , W , l(m), l(w)}. They proposed the al-
gorithm of Gale-Shapley (GS ) to find M with com-
plexity O(n
2
).
Since then, this optimization problem was con-
stantly one among the most popular in combina-
torics from both theoretical (McVitie and Wilson,
1971), (K. Iwama and Morita, 1999),(D.F. Manlove
et al., 2002), (Gent and Prosser, 2002), (McVi-
tie and Wilson, 1971) and practical points of view
(D. Bianco and Larimer, 2001), (C.P. Teo and Tan,
1999), (T. Kavitha and Paluch, 2004). According to
(K. Iwama and Morita, 1999), the stable marriage
problem was studied and generalized in 4 directions:
(i) stable marriage with complete list and total or-
der, the case of Gale and Shapley; (ii) stable marriage
with incomplete list and total order (Manlove, 1999),
(iii) stable marriage with complete list and indiffer-
ence (Irving, 1994), and (iv) stable marriage with in-
complete list and indifference (K. Iwama and Morita,
1999).
GS has usually two different solutions, men-
optimal and women-optimal depending whom is
asked first to choose. Men-optimal brings a stable
matching in which men have the best possible part-
ner and women may have the worst and conversely.
In many applications of such optimization on bi-
partite graphs, as resource scheduling, there might
be reasons why to favour one sub-population: for
instance demand constraints are economically more
63
Y. Zavidovique B., Suvonvorn N. and S. Seetharaman G. (2005).
A NOVEL REPRESENTATION AND ALGORITHMS FOR (QUASI) STABLE MARRIAGES.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 63-70
DOI: 10.5220/0001159900630070
Copyright
c
SciTePress

important than supply ones, or teachers constraints
might be more strict than class-rooms ones. In many
other such problems like segment-pairing in robot vi-
sion for stereo reconstruction, motion understanding
or object recognition there is an a priori equal im-
portance of both sets of segments respectively ex-
tracted from a couple of images or from the model
(Bouchafa and Zavidovique, ), (J.L.Lisani et al.,
2001), (Monasse and Guichard, 1998), (Ballester
et al., 1998), (Caselles et al., 1999) : then sex equal-
ity is likely worth accounting for, leading to a fair
algorithm. Moreover, some global satisfaction from
the matching may translate a better balanced solution
among the many possible ones. Neither one is guar-
anteed by GS : the obtained stable matching can be
such that everybody is unsatisfied. A last difficulty
comes from the order in which men or women are
considered inside their own sub-set, it can influence
the result.
In this article, we propose a stable marriages al-
gorithm based on a novel representation, called mar-
riage table. The new algorithm fits stable marriages
with complete/incomplete list and total order. It aims
at stability, sex equality and global satisfaction.
2 NOVEL REPRESENTATION OF
THE STABLE MARRIAGES
PROBLEM
In order to build an algorithm that had a chance
to meet the three criteria of stability, sex equality
and global satisfaction, we first change representa-
tion. The so-called marriage table translates and sup-
plements the preference lists. Stable matchings are
looked for by scanning this latter array and suitable
properties of the solution are associated to the type of
scan. The marriage table is a table with (n + 1) lines
and (n + 1) columns. Lines (resp. columns) frame
the preference orders of men, {1 · · · p · · · N ∞} (resp.
women, {1 · · · q · · · N ∞}). The cell (p, q) contains
pairs (m, w) such that w is the p
th
choice of m, and
m is the q
th
choice of w. Cells can thus contain more
than one pair or none. The cell (p, ∞) (resp. (∞, q))
contains the pairs where the woman is the p
th
choice
of the man (resp the q
th
choice of the woman) but the
man does not exist in her preference list (resp. the
woman is not in his preference list). A key feature of
this table in the ”complete list” case is that each line
contains all men once and each column contains all
women once. The figure 1 shows a typical marriage
table.
The table 1 is the example of an instance of three
men and women. Every man or woman made their
preference list. The figure 2 is the marriage table and
stable matching established from the population 1.
1
1 2 3 4 q
2
3
4
n
(x,y)
p
n
∞
∞
Figure 1: Marriage table : the pair (x,y), y is the 3
rd
choice
of x and x is the 4
th
choice of y
Table 1: An instance of 3 men and women and their prefer-
ence lists
Men Women
1 : C, A, B A : 1, 2, 3
2 : A, C, B B : 2, 3, 1
3 : C, B, A C : 1, 2, 3
One advantage of the marriage table is that satis-
faction and equality of sex show concurrently in the
same representation.
For instance let us define a global satisfaction by:
S =
X
(m,w)∈M
(ρ
m
+ ρ
w
) (1)
Intuitively, the closer S to zero the greater global
satisfaction: in average more people are satisfied. A
solution with maximum global satisfaction would dis-
play matched pairs as close around the origin (table
bottom-left) as mutual exclusion allows. More gen-
erally the table representation is indicative of a result
global satisfaction through the lay out of the selected
couples. Satisfaction is constant along antidiagonals
(straight lines of equation p + q = constant) and de-
creasing with the distance to the origin . And that
provides some criteria to design scans of the marriage
table that could favour better global solutions.
Conversely, sex equality tends to fit the diagonal of
the marriage table. Let us define it as
S =
X
(m,w)∈M
|ρ
m
− ρ
w
| (2)
Intuitively the closer to the diagonal the more bal-
anced treatment. Elements of a pair in a cell close to
the diagonal are equally satisfied or unsatisfied, de-
pending on the distance to the origin. The smaller the
greater equity. And again that provides some criteria
to design scans of the marriage table that could favour
more equitable solutions.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
64

1
2
3
p
1 2 3 q
(3,C)
(2,A)(1,C)
(1,A)
(2,C)
(3,B)
(3,A)
(1,B)
(2,B)
∞
∞
(3,A)
1
2
3
p
1 2 3 q
(3,C)
(2,A)(1,C)
(1,A)
(2,C)
(3,B)
(2,B)
(1,B)
∞
∞
(a) (b)
Figure 2: (a) Marriage table established from the table 1 (b)
Matching result : (1,C), (2,A) and (3,B).
Stability gets a graphic translation too in the mar-
riage table. In the case of complete preference lists, a
blocking situation is represented figure 3. Assuming
(x, t) and (z, y) were respectively paired, then (x, y)
cannot be in the grey rectangle and (z, t) cannot be in
the dashed one. These constraints will help building a
new algorithm. In the case of uncomplete preference
lists an additionnal blocking situation is when m and
w are not matched in M but m finds w acceptable and
w finds m acceptable.
(z, y)
p
q
(x, y)
(z, t)
(x, t)
Figure 3: Blocking situation in a marriage table.
3 MARRIAGES AND TABLE
SCANS
Algorithms can now be designed to find marriages
that would globally guarantee one or the other prop-
erty. Any selection process is a scan of the marriage
table along which couples are stored or not and then
released or not depending on circumstances. After the
analysis above, suitable scans to meet all constraints
should be zig-zag ones that trade off between the first
and second diagonal directions. Considering a priori
symmetries of the marriage table, scanning from left
to right or conversely does not matter statistically and
same for scanning from origin to top or conversely.
Indeed, given an instance, changing man’s lists into
woman’s lists makes it for the right/left invariance
and complementing preferences to the population-
size makes it for the top-bottom invariance. We study
experimentally three strategies here (zigzag ZZ with
man-optimal or woman-optimal, optimal (symmetric)
zigzag OZ , blocked zigzag BZ ) and then compare
the results with GS in a systematic way: 200 in-
stances are built at random for populations of 5, 10,
50, 100, 150 and 200 respectively. Each algorithm is
run on the populations and for each one the following
plots are displayed and analyzed: global satisfaction
vs instances index, fairness vs instances index and, in
case there are, number of blocking pairs vs popula-
tions.
3.1 Zigzag with man-optimal or
woman-optimal (ZZ )
It appears from the global satisfaction graph (figure
4) that its patterns present some similarity ( min/max,
σ) by sample of 50. We pick up 40 consecutive in-
stances at random for display to show results more in
details. From the figure 5, one can see that the global
satisfaction obtained by ZZ is better in average than
the one by GS . Its variation is also smaller, meaning
that results from ZZ are more consistent (hence more
reliable to global matching) than by GS .
Figure 4: Comparing global satisfaction between meth-
ods: (a) GS man-optimal (b) GS woman-optimal (c) Zigzag
man-optimal and (d) Zigzag woman-optimal, in case of 150
large populations.
Figure 6 shows the same sample of 40 instances
for sex equality. Trends of that type of plot are very
similar to global satisfaction trends. The jittery pat-
tern of GS s are similar for global satisfaction and sex
equality, with average standard deviation in the range
of 40 to 50%. In both cases, strong variations from
one instance to the next one show qualitative same
tendancies, contrasting with comparatively bounded
variations by ZZ (15 to 20%). In average ZZ per-
forms twice as well as GS (3500 vs. 4800 and 1800
A NOVEL REPRESENTATION AND ALGORITHMS FOR (QUASI) STABLE MARRIAGES
65

Figure 5: Close up on global satisfaction between meth-
ods: (a) GS man-optimal (b) GS woman-optimal (c) Zigzag
man-optimal and (d) Zigzag woman-optimal
vs. 3800). However the improvement is much more
significant regarding sex equality that is genuinely de-
nied by GS . Moreover, if one considers the number
b of instances where ZZ is better than GS , defined as
b =
X
all instances
Y
[min(GS
m
,GS
w
)−max(ZZ
m
,ZZ
w
)]
(3)
with
Y
x
= 1 if x > 0
Y
x
= 0 else
and
β =
100×b
number of instances
β = 96% for global satisfaction and β = 99% for
sex equality. This percentage depends directly on the
population size. The larger population, the greater im-
provement. Experimentally, beyond 200 large popu-
lations ZZ becomes 100 percent better than GS for
both global satisfaction and sex equality.
Figure 6: Comparison of sex equality between the meth-
ods: (a) GS man-optimal (b) GS woman-optimal (c) Zigzag
man-optimal and (d) Zigzag woman-optimal
However, matching stability is not guaranteed by
ZZ . As a gauge of unstability, figure 7 (a) and (b)
display the average number of blocking pairs with
their standard deviations vs. the population size. Note
that cases (a) and (b), respectively ZZ man first and
ZZ women first, are unseparable at that representa-
tion scale. It appears that the larger, the less stable.
Figure 7: The average number of blocking pairs using: (a)
Zigzag man-optimal and (b) Zigzag woman-optimal (c) Op-
timal zigzag (d) Blocked zigzag
3.2 Optimal (Symmetric) zigzag
(OZ )
The primary implementation of a diagonal scan of the
marriage table proves significantly better than GS as
for global satisfaction and fairness. But the scan start
direction - men or women first - still matters in ex-
treme cases, although its impact is less in general. We
now propose an algorithm (algo.1) that targets opti-
mal zigzag from bottom-left to top-right (forward).
Here again, anti-diagonals of the table are scanned
forward from maximum to minimum global satisfac-
tion but each one is read in swinging from center to
sides meaning maximum to minimum sex equality.
With this algorithm global satisfaction is considered
first and then sex equality. Figures 8(c) and 9(c) show
the global satisfaction and sex equality compared with
GS 8(a)(b) and 9(a)(b) respectively. Both global sat-
isfaction and sex equality slightly worsen compared
to ZZ ,but the main result is blocking pair numbers de-
crease significantly by about 40% (figure 7 (c)). Still,
the method does not guarantee any matching stability.
The complexity for all these algorithms so far remains
in O(n
2
), table building included.
3.3 Blocked zigzag (BZ )
Both previous algorithms provide matching solutions
that are globally satisfactory and fair but unstable:
they might even be such that everybody would like
to move!. In this section an algorithm (algo.2) is de-
signed to meet all three criteria concurrently, to the
price of reasonnable increase in complexity due to
systematic test added. We scan anti-diagonals same
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
66

1: Optimal zigzag algorithm
begin
foreach anti-diagonal, maximum to miminum
global satisfaction do
foreach diagonal, maximum to miminum
sex equality in alternate directions do
foreach pair (m, w) do
if m et w are free then
Marry m with w
end
as before. In each cell, all pairs are accepted for mar-
riage if their components are free. After all cells have
been considered, the table is then revisited up to com-
plete removal of blocking situations as follows: po-
tential blocking pairs are matched upon detection (test
according to figure 3) while both blocked couples are
broken and complementary elements are freed. To
overcome cycles in the assignment the number of res-
canning is limited to the population size. Scan di-
rections together with questionning all previous mar-
riages on demand guarantees the better at end. Global
satisfaction and sex equality are comparable to for-
mer ones (figure 8(d) and 9(d)) if not even better. The
main improvement is matching stability now obtained
in a great majority of cases, with the number of un-
stabilities significantly lowered otherwise (see figure
7(d)). More precisely, the number of blocking pairs
is null until 50 man-or-woman large populations. It
is still 0 in an average 96% of the 200 instances for
populations larger than 50, and its maximum ranges
in the 15 blocking pairs for 100. However, the algo-
rithm complexity is in the order O(n
3
).
In figure 10, the algorithm performances are com-
pared wrt. population size. The improvement β from
GS to BZ increases with the population size. Again,
beyond 100 large populations ZZ becomes 100 per-
cent better than GS for both global satisfaction and
sex equality.
4 APPLICATIONS
For sake of illustration we outline here three im-
age processing applications in stereovision, registra-
tion and motion analysis. Matching relies on level-
lines. Features as simple as junctions or sequences
of line segments are extracted from each image and
then selected into primitives. Each primitive is given
its preference list containing primitives of the other
image (see for instance figure 11). The preference
list is incomplete and sorted by features similarity
(e.g. contrast, length, relative orientation, relative
2: Blocked zigzag algorithm
begin
while there is a bloking pair and rescan
number < population size do
foreach anti-diagonal, maximum to
miminum global satisfaction do
foreach diagonal, maximum to
miminum sex equality back and forth
do
foreach pair (m, w) do
if m and w are free then
Marry m with w
foreach anti-diagonal, maximum to
miminum global satisfaction do
foreach diagonal, maximum to
miminum sex equality back and forth
do
foreach pair (m, w) do
if (m, w) is blocking pair
then
Free m and w and their
spouse
Marry m with w
end
position etc.). Blocked zigzag is then run. Figure
12(a)(b)(c)(d) show the original stereo images and the
features in them respectively. The result of feature
matching by BZ shows as an optical flow in figure
12(e). And the figure 12(f) supports comparison with
GS . Results are quite comparable to the naked eye
due to the ”incomplete list” nature of the implemen-
tation.
The same process can do for motion. Figures 13
show the image sequence and the matching result re-
spectively.
5 CONCLUSION
In this paper, we proposed and evaluated ”stable mar-
riages” algorithms based on a novel representation,
called marriage table. Its definition and properties are
presented. Algorithms follow different scan styles of
the latter table, defining result properties accordingly.
We introduce three different ones to progressively
meet three criteria: global satisfaction, sex equality
and stability. The three criteria together (quasi) satis-
fied change complexity from O(n
2
) to O(n
3
). Match-
A NOVEL REPRESENTATION AND ALGORITHMS FOR (QUASI) STABLE MARRIAGES
67
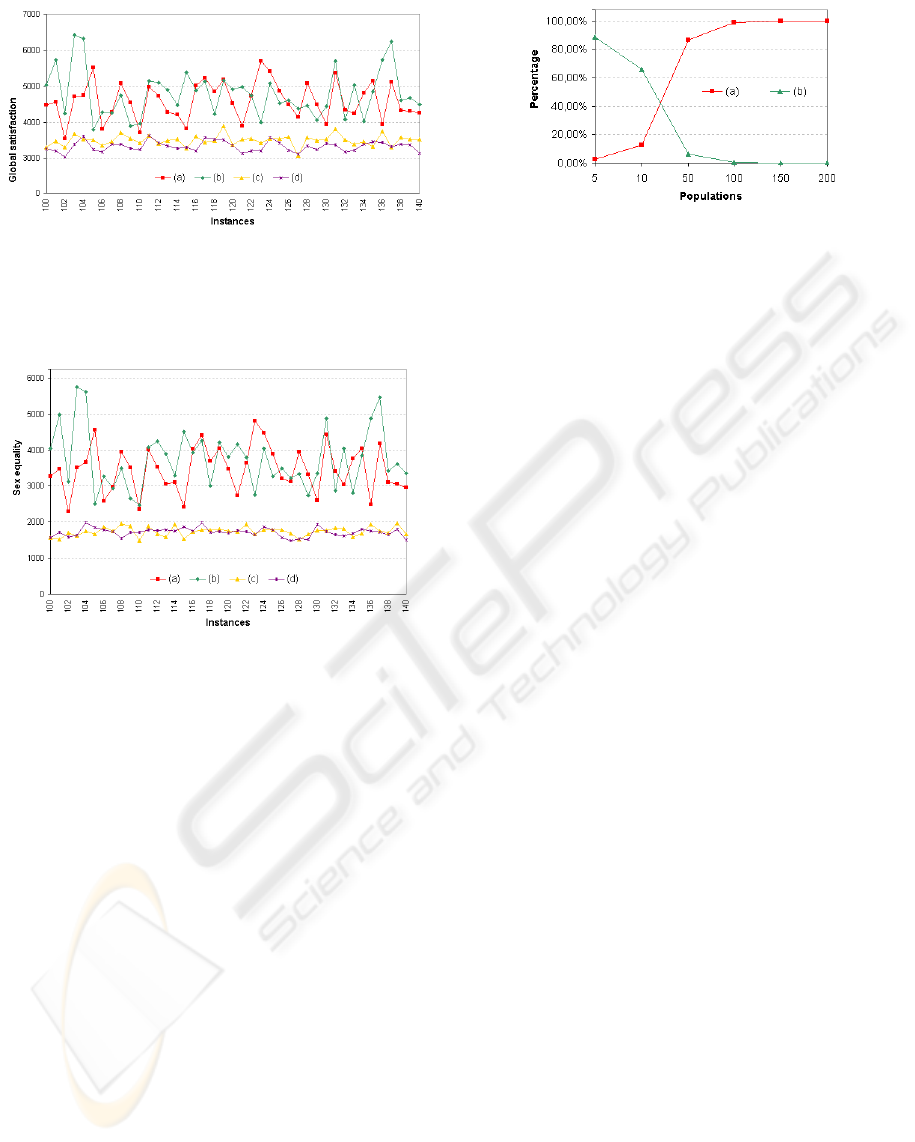
Figure 8: Comparison of global satisfaction between the
methods: (a) GS man-optimal (b) GS woman-optimal (c)
Optimal zigzag and (d) Blocked zigzag, with 200 instances
of 150 large populations.
Figure 9: Comparison of sex equality between the meth-
ods: (a) GS man-optimal (b) GS woman-optimal (c) Opti-
mal zigzag and (d) Blocked zigzag
ing results obtained are systematically and experi-
mentally compared to GS
′
s. Some application re-
sults in motion analysis, registration and stereovision
are also given just for illustration.
REFERENCES
Abeledo, H. and Rothblum, U. G. (1995). Paths to marriage
stability. Elsevier : Discrete Applied Mathematics,
63(1-12).
Ballester, C., Castan, E., Gonzalez, M., and Morel,
J. (1998). Contrast invariant image intersection.
C.M.L.A, (9817).
Bouchafa, S. and Zavidovique, B. Stratgie de vote pour la
mise en correspondance de lignes de niveaux. Univer-
sit Paris-Sud, AXIS.
Caselles, V., Coll, B., and Morel, J. (1999). Topographic
maps and local contrast changes in natural images. In-
ternational Journal of Computer Vision, 33(1):5–27.
C.P. Teo, J. S. and Tan, W. (1999). Gale-shapley stable mar-
Figure 10: Performance comparison between GS and BZ
algorithms
riage problem revisited: Strategic issues and applica-
tions. IPCO’99, pages 429–438.
D. Bianco, S. H. and Larimer, A. (2001). Stable matchings
in the couples problem. Morehead Electronic Journal
of Applicable Mathematics, 2.
D.F. Manlove, R.W. Irving, K. I., Miyazaki, S., and Morita,
Y. (2002). Hard variants of stable marriage. Theoreti-
cal Computer Science, 276(1-2):261–279.
Diamantoudi, E., Miyagama, E., and Xue, L. (2004). Ran-
dom paths to stability in the roommate problem. Else-
vier : Games and Economic Behavior, 48(18-28).
Gale, D. and Shapley, L. (1962). College admissions and
the stability of marriage. American Mathematical
Monthly, 69:9–15.
Gent, I. and Prosser, P. (2002). An empirical study of
the stable marriage problem with ties and incom-
plete lists. Technical Report APES-40-2002, APES
Research Group. Available from http://www.dcs.st-
and.ac.uk/ apes/apesreports.html.
Irving, R. (1994). Stable marriage and indifference. Dis-
crete Applied Mathematics, 48:261–272.
J.L.Lisani, Monasse, P., and Rudin, L. (2001). Fast shape
extraction and applications. C.M.L.A, (2001-16).
K. Iwama, D. Manlove, S. M. and Morita, Y. (1999). Stable
marriage with incomplete lists and ties. Proceedings
of ICALP ’99: the 26th International Colloquium on
Automata, Languages and Programming, 1644:443–
452.
Manlove, D. (1999). Stable marriage with ties and un-
acceptable partners. Technical Report TR-1999-29,
Computing Science Department of Glasgow Univer-
sity.
McVitie, D. G. and Wilson, L. B. (1971). Three procedures
for the stable marriage problem. Communications of
the ACM, 14,7:491–492.
Monasse, P. and Guichard, F. (1998). Fast computation of a
contrast-invariant image representation. IEEE Trans.
on Image Proc., 9(5):860–872.
T. Kavitha, K. Mehlhorn, D. M. and Paluch, K. (2004).
Strongly stable matching in time o(nm) and extension
to the hospitals-residents problem. STACS’04, pages
222–233.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
68
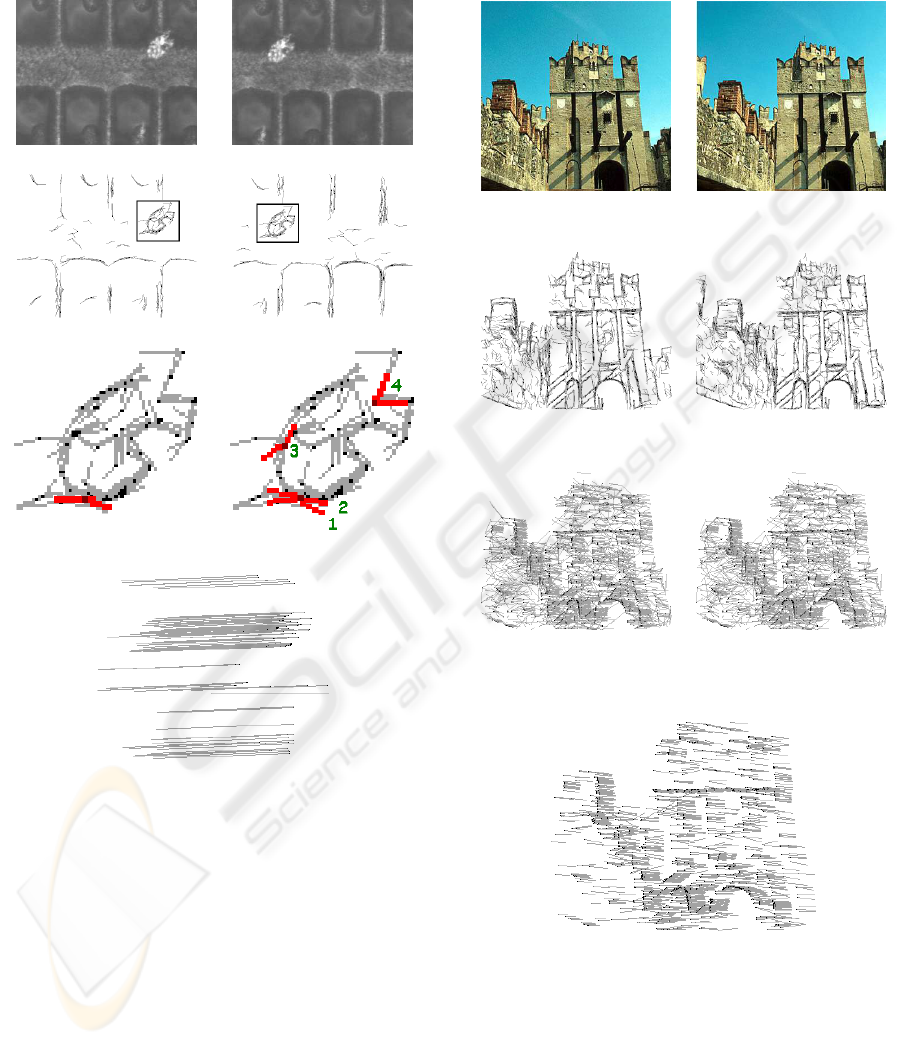
(a) (b)
(c) (d)
(e) (f)
(g)
Figure 11: Stable marriages for MEMS images registration
in electron beam microscopy, (a) 1
st
field part scaned, (b)
2
nd
field part scaned to be super imposed into a larger field.
Let us underline the VLSI implementation artefact : this
defect will eventually support the perfect match between
(a) and (b), despiste the cumb ambiquity from periodicity,
(c)(d) the primitives extracted from (a) and (b) with primi-
tives from the defect underlined in the frame, (e) primitives
in the defect that supports the perfect piecing, (f) potential
mates of the primitive underlined in bold in (e) with their
rank, (g) final matching results by BZ : the are in perfect
agreement with the known reality
(a) (b)
(c) (d)
(e) (f)
(g)
Figure 12: Stable marriages matching for stereovision,
(a)(b) stereo images, (c)(d) features extracted from (a)(b)
respectively, (e) matching results by BZ, (f) matching re-
sults by GS, (g) final matching results by BZ
A NOVEL REPRESENTATION AND ALGORITHMS FOR (QUASI) STABLE MARRIAGES
69

(a)
(b)
(c)
(d)
Figure 13: (a)(b)(c) Image sequence for motion detection,
(d) Matching result by using the stable marriages algorithm.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
70
