A MODEL BASED HYBRID NUMERICAL CONTROL

ALGORITHM FOR THE CONTINUOUS DRYING OF A THICK

WEB IN AN INFRARED DRYER

Normand Thérien, Arthur Broadbent

Département de génie chimique, Faculté de génie, Université de Sherbrooke, Sherbrooke, Québec, Canada

Sergio Pérez

Departamento de Ingeniería Química, Facultad de Ingeniería, Universidad de Carabobo, Valencia, Venezuela

Keywords: Infrared drying, thick web drying, Model-based numerical control.

Abstract: Experimental results from the transient drying of sheets of polyester in an infrared (IR) dryer were used to

derive a performance model. Separate drying experiments were done using sheets of material of various

densities and thicknesses. The formulations expressed the core temperature of the web to the surface

temperature of the web as a function of the residency time in the dryer and the electric power used. Also, a

relationship between the time duration required to achieve a given core temperature of the web as a function

of the electric power was derived. These relationships were used to derive an hybrid numerical control

algorithm using feed forward and feedback actions to control the core humidity of the web at the outlet of

the dryer.

1 INTRODUCTION

The numerical control of the humidity of a thin sheet

of material being continuously dried in an infrared

oven has been achieved with success in the past

(Dhib et al., 1999). However, this is no longer the

case when a thick web is considered for drying. Two

major difficulties arise. One is linked with the

existence of a significant humidity and temperature

gradient across the thickness of the sheet of material

as it travels in the oven. The second problem is the

difficulty of measuring the core humidity and the

internal temperature of the web during the drying

process. For these reasons, a set of experiments were

designed to characterize the evolution of the water

content and temperature profile inside the web

during drying in an infrared oven. To this end, webs

of various densities and thicknesses were used.

2 EXPERIMENTAL SET-UP

Separate batch drying experiments were done using

sheets of polyester with densities of 200 g/m

, 800

g/m

and 2000 g/m

. The sheets were 1.3 mm thick,

5.2 mm thick and 15.8 mm thick respectively.

Thermocouples were imbedded at separate locations

across the thickness of the web. They permitted the

continuous measurements of the internal temperature

during the drying process. At given times, samples

of material were removed locally at specific depths

of the web to determine the average water content.

Surface temperature of the web was measured using

both surface thermocouples and infrared optical

pyrometers (Ircon). Humidity at the surface of the

web was also measured using high-frequency

humidity meters (Labtec). Infrared flux

measurement was done using a Schmidt-Boelter

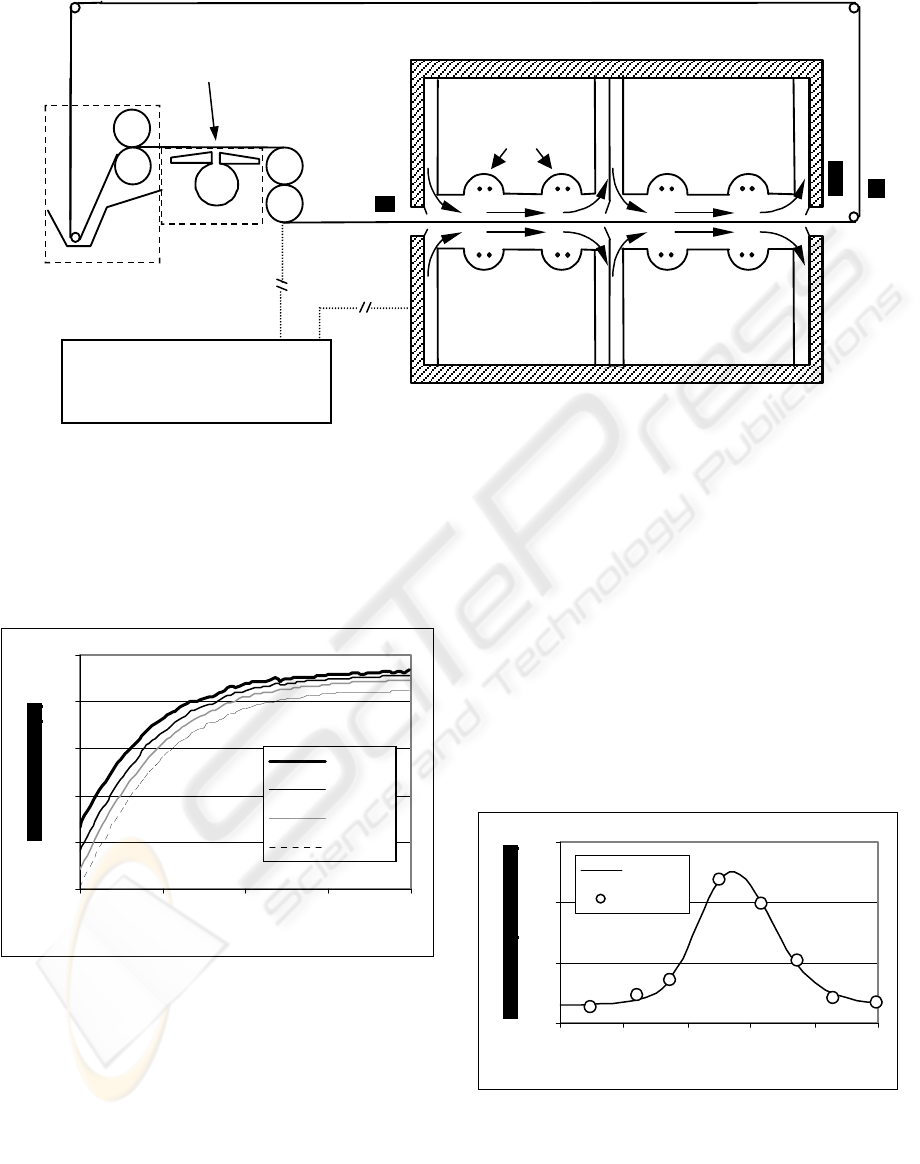
type flux meter. Figure 1 illustrates the experimental

set-up.

3 RESULTS

All of the drying experiments were made on

stationary sheets in the oven. Evolutions of

temperature at different depths across the web

thickness were followed as a function of time.

324

Thérien N., Broadbent A. and Pérez S. (2005).

A MODEL BASED HYBRID NUMERICAL CONTROL ALGORITHM FOR THE CONTINUOUS DRYING OF A THICK WEB IN AN INFRARED DRYER.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 324-327

DOI: 10.5220/0001160103240327

 SciTePress

Separate experiments were done using electrical

power ranging from 1300 watts to 2180 watts.

Results are reported for the 15,6 mm thick polyester

sheet having a density of 2000 g/m

. Figure 2

illustrates the results obtained when operating the

oven at 1740 watts. At each separate location, the

temperature tends to level off until the water is fully

evaporated. When this occurs, about one hour after

start-up, the temperature will rise sharply (not shown

on Figure 1). Also, the humidity of the sheet at

different depths of the web was determined at

specific times after start-up. Figure 3 illustrates the

humidity profile observed after 3000 seconds.

Radiant energy is furnished on both sides of the web

and a very nearly symmetrical humidity profile is

observed. During drying the water content is always

highest at the web mid-depth and lowest at the top

and bottom of the web. Similar results were obtained

with sheets of different densities and thicknesses

when operating the oven at other electrical power

levels in the range indicated. The humidity patterns

observed show similarities to the ones reported by

(Jones, 1969) during contact drying of a thick sheet

of paper.

Nonetheless, it is impossible to measure the

internal humidity and temperature of the web during

continuous drying as the web travels inside the oven.

The only measurements possible are the external

humidity and temperature at the surface of the web

0 250 500 750 1000

TIME (SEC)

2,6 mm

3,8 mm

5,2 mm

7,6 mm

Figure 2: Evolution of temperature at different depths

of a 2000g/m

polyester sheet - 1740 watts

0,4

0,6

0,8

03691215

DEPTH (M M )

MODEL

DATA

Figure 3: Humidity inside a 15,6 mm thick 2000g/m

polyester sheet after 3000 seconds - 1740 watts

INFRARED OVEN

WEB

COMPUTER SYSTEM

CONTROL ALGORITHM

P : PYROMETER

RADIANT

EMITTERS

WETTING BATH

VACUUM SLOT

AIR

H : HUMIDITY METER

Figure 1: Infrared dryer system.

Figure 1: Infrared dryer system

A MODEL BASED HYBRID NUMERICAL CONTROL ALGORITHM FOR THE CONTINUOUS DRYING OF A

THICK WEB IN AN INFRARED DRYER

325

under these conditions. Moreover, this can only be

done at the outlet of the oven considering the radiant

flux of energy inside the oven. A way of dealing

with this problem is to relate ultimately the humidity

and temperature at the web surface to the internal

humidity and temperature of the web using a model.

A phenomenological model for the radiant drying of

thick sheet of porous material derived by Kuang et

al. (1994) considering the many transport

phenomena involved during drying offered the

potential of doing that. Unfortunately, the

mathematical solution of this partial differential

model is too time intensive and the formulation does

not lead itself easily to implementation for real time

control. This is especially true when operating the

oven at higher electrical power levels for which

much shorter drying time responses would be

observed. However, further analysis of the results

obtained during the set of experiments done here has

indicated drying characteristics that can be used to

profit in a control algorithm.

First, as illustrated in Figure 4, results have

indicated that the time interval required such that the

core temperature at the mid-depth of the web

achieves 100 ºC (a completely dry condition) is a

linear function of the electrical power used in the

oven. Also, as indicated in Figure 5, results have

shown that the temperature at the external surface of

the web, corresponding to a internal temperature

reaching 100 ºC at mid-depth of the web, is also a

linear function of the electrical power used in the

oven. These characteristics have been shown to hold

with webs of different densities and thicknesses in

the range of the electrical power indicated.

4 MODEL BASED CONTROL

The experimental results have shown that the surface

temperature of the web T

at the outlet of the oven

is linearly related to the electrical power used:

= A

. P + B

. θ (1)

Also, the residency time required to achieve a given

temperature T

at mid-depth across the thickness of

the web at the outlet of the oven was shown to be

linearly related to the electrical power used. In a

more general fashion :

= A

. P + B

. θ (2)

In both cases, A

, A

, B

and B

are scalars whose

values depend generally on the humidity of the web

inlet

at the inlet of the oven and must be determined

through experimentation (Slitine et al., 2001).

Generally, this would need to be done for a range of

humidity (water content of the web) typical of the

ones existing at the point of entry to the oven.

Fortunately, the humidity of the web entering the

oven is often limited to a small range of values. In

effect, excess water has normally been removed

since the material entering the oven is generally

passed through a free water removing device rollers

or vacuum slot (see Figure 1). Nevertheless, the

scalars A

, A

, B

and B

need be determined

specifically for each type of material (density and

thickness) considered for drying. For a given

residency time in the oven, Equation (2) may be

used to compute the a priori electrical power

required to achieve a desired core temperature T

mid-depth across the thickness of the web :

P = (T

/ A

) - (B

/ A

) . θ (3)

Also, through equations (1) and (2) T

is related to

and P in the following manner:

= (B

). T

+ B

. P (4)

275

300

325

350

375

1000 1500 2000 2500

ELECTRICAL POWER (WATTS)

Figure 4: Time required achieving 100 ºC at mid-

depth of a 15,6 mm thick 2000g/m

polyester sheet as

a function of power input

150

175

200

225

250

1000 1500 2000 2500

ELECTRICAL POWER (WATTS)

Figure 5: Surface temperature of a 15,6 mm thick

2000g/m

polyester sheet when reaching 100 ºC at

mid-depth as a function of power input

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

326

Therefore, the set point for the surface temperature

at the outlet of the oven achieving a given core

temperature of the web at mid-depth, reflecting a

chosen drying condition, may be computed by

equation (4). Although choosing T

= 100 ºC will

ensure full and rapid drying of the web, this is not a

requirement and may even not be desirable. In

effect, such a choice will lead to a much higher

temperature at the surface of the web (see Figure 5)

that could adversely affect the surface quality of the

material. Results shown in Figure 2 and results from

other drying experiments with thick sheets of

material in an IR oven (Thérien, 1997) have

indicated that much lower values of T

can be used

to produce satisfactory results.

Based on the previous relationships it is possible

to design a hybrid control strategy for the drying of

thick webs in an IR oven. The basic structure of the

control strategy is illustrated in Figure 6. The

following algorithm gives the necessary steps

required to implement it:

1) Reading of the web velocity V in the oven

2) Computation of the residency time θ of the web

in the oven of length L, θ = L/V

3) Reading of the web humidity H

inlet

at the oven

inlet

4) Computation of coefficients A

, B

and B

corresponding to H

inlet

5) Computation from equation (3) of the electrical

power required P (feedforward action) for a

chosen value of T

6) Computation from equation (4) of the set point

for T

7) Measurement of T

at the oven outlet

8) Adjustment of P (feedback mode) through a

given controller (PID, Dahlin, etc) to correct for

the model prediction error (feedforward action)

in step 5

5 CONCLUSION

Drying experiments of thick webs in an IR oven

have shown linear relationships between the surface

temperature of the web and the core temperature at

mid-depth across the thickness of the web and the

electrical power used for drying. These relationships

have permitted the elaboration of a hybrid

feedforward-feedback control strategy for the drying

of thick sheets of material in an IR oven.

REFERENCES

Dhib, R., N. Thérien and A.D. Broadbent, 1999. Model-

based Multivariable Control of the Drying of a Thin

Sheet of Fibers in a Continuous Infrared Dryer, Can. J.

Chem. Eng., 77, A7 (6), 1055-1064.

Jones, G., 1969. The hot surface drying of fibre mats,

Ph.D. Thesis, University of Manchester, 222 pages.

Kuang, H.D., Thibault, J. and B. P. A. Granjean, 1994.

Study of heat and mass transfer during IR drying of

paper, Drying technology, 12 (3), 545-575.

Slitine, D.S., Thérien, N. and A.D. Broadbent, 2001. Real-

Time Parameter Identification for a Control-Oriented

Model of the Continuous Drying of a Wet Fabric,

Textile Research Journal, 71 (1), 31-37.

Thérien, N., 1997. Modélisation des nappes épaisses par

rayonnement infrarouge. Rapport final. LTÉÉ.

Shawinigan, Québec. 76 pages + Annex.

INFRARED OVEN

INLET WEB

HUMIDITY

SET POINT

FOR TSS

(EQUATION 4)

ERROR

SET POINT

FOR TCC

FEEDBACK

CONTROLLER

FEEDFORWARD

COMPUTATION OF P

(EQUATION 3)

TSS

Figure 6: Hybrid feedforward and feedback control scheme.

Figure 6: Hybrid feedforward and feelback control scheme

A MODEL BASED HYBRID NUMERICAL CONTROL ALGORITHM FOR THE CONTINUOUS DRYING OF A

THICK WEB IN AN INFRARED DRYER

327