
AN EXPLORATION MEASURE OF THE DIVERSITY
VARIATION IN GENETIC ALGORITHMS
G. A. Papakostas, Y. S. Boutalis
Democritus University of Thrace, Department of Electrical and Computer Engineering, 67100 Xanthi, Hellas
D. A. Karras
Chalkis Institute of Technology, Automation Dept. and Hellenic Open University, Ano Iliupolis, Athens 16342, Hellas
B. G. Mertzios
Thessaloniki Institute of Technolog, Department of Automation, Laboratory of Control Sys. and Comp. Intell., Hellas
Keywords: Genetic Algorithms, Diversity, Clustering.
Abstract: In this paper, a novel measure of the population diversity of a Genetic Algorithm (GA) is presented.
Chromosomes diversity plays a major role for the successfully operation of a GA, since it describes the
number of the different candidate solutions that the algorithm evaluates, in order to find the optimal one, in
respect to a performance index, called objective function. In a well defined algorithm, the diversity of the
current population should be measurable, in order to estimate the performance of the algorithm. The resulted
observation, that is, the measuring of the diversity, can then be used to real-time adjust the factors that
determine the chromosomes variety (P
c
, P
m
), during the execution of the GA. It is shown, that a simple
chromosomes clustering into the search space, by using the well known k-means algorithm, can give a
useful picture of the population’s distribution. Thus, by translating the problem of finding the best solution
to a GA-based problem into an iterative clustering process, and by using the scatter matrices (S
w
, S
b
), which
describe completely the candidate’s solutions topology, one could define a novel formula that gives the
population diversity of the algorithm.
1 INTRODUCTION
Evolutionary Algorithms (EAs) have been used in
many applications through the years, due to its
stochastic mechanism for finding solutions that
optimize single or multiple objective problems.
Genetic Algorithms (Holland, 2001, Mitchell, 2002)
are considered the most popular kind of EAs since
they are characterized by a high degree of parallism
and natural behaviour.
Genetic Algorithms (GAs) are used as
optimization methods to solve difficult and complex
problems in a range of scientific fields, such as
image processing (Mirmehdi, 1997, Papakostas,
2003), robust control (Jamshidi, 2003, Papakostas,
2004), pattern
classification (Bandyopadhyay, 1995)
etc. Their popularity can be justified by their ability
to overcome possible local optima, and to converge
to the global solution of a problem, with high
probability.
However, there are some cases in which the
global optimum is quite far from the derived
solution that the algorithm converged to. This
undesirable situation is called premature
convergence (Mitchell, 2002). When this
phenomenon appears, the population chromosomes
are all the same. In other words, the population
diversity has been lost. Of course, the diversity
would be also lost in the case of the algorithm
converging to the global optimum. The ill-posed
situation is when the diversity
decreases quickly and
stays to low level for many generations.
Therefore, in order to prevent this situation, it is
needed to measure the diversity variation through
the generations, and adjust the algorithm parameters
off-line, in the initial calibration or online during the
execution of the algorithm.
260
A. Papakostas G., S. Boutalis Y., A. Karras D. and G. Mertzios B. (2005).
AN EXPLORATION MEASURE OF THE DIVERSITY.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 260-265
Copyright
c
SciTePress
In the present paper, a clustering method for
exploring the distribution of the chromosomes and
the scatter matrices, S
b
– between class scatter
matrix and S
w
– within class scatter matrix of the
resulted clusters for measuring the level of the
current diversity, are being used.
The paper is organized as follows: the proposed
method is described in section 2, by analyzing the k-
means algorithm and the way it is used for this paper
purpose, while the effectiveness of the method is
examined through appropriate simulations in the
third section. Finally, conclusions that may derive
from the previous discussion are highlighted in the
last section.
2 THE PROPOSED METHOD
The main idea of the proposed method, for
measuring the population diversity of a GA, is based
on viewing the process to find the optimal solution
of a problem, as a clustering one. Let us consider the
algorithm’s chromosomes for an n-dimensional
problem
)...(...,),...(
321
11
3
1
2
1
11
m
n
mmm
mn
xxxxChxxxxCh
where Ch
i
is the i
th
chromosome, and
i
j
x is the j
th
variable of the i
th
chromosome. In the above
formulation, the population size is equal to m.
These chromosomes can be considered as n-
dimensional vectors with coordinates (x
1
,x
2
,…,x
n
),
and thus can be considered as single points into the
n-dimensional variable space (search space). To
visualize these points in the search space, one can
produce the scatter plot of them, as depicted in the
following figure, where the points correspond to the
initial population in the case of a 2-D problem.
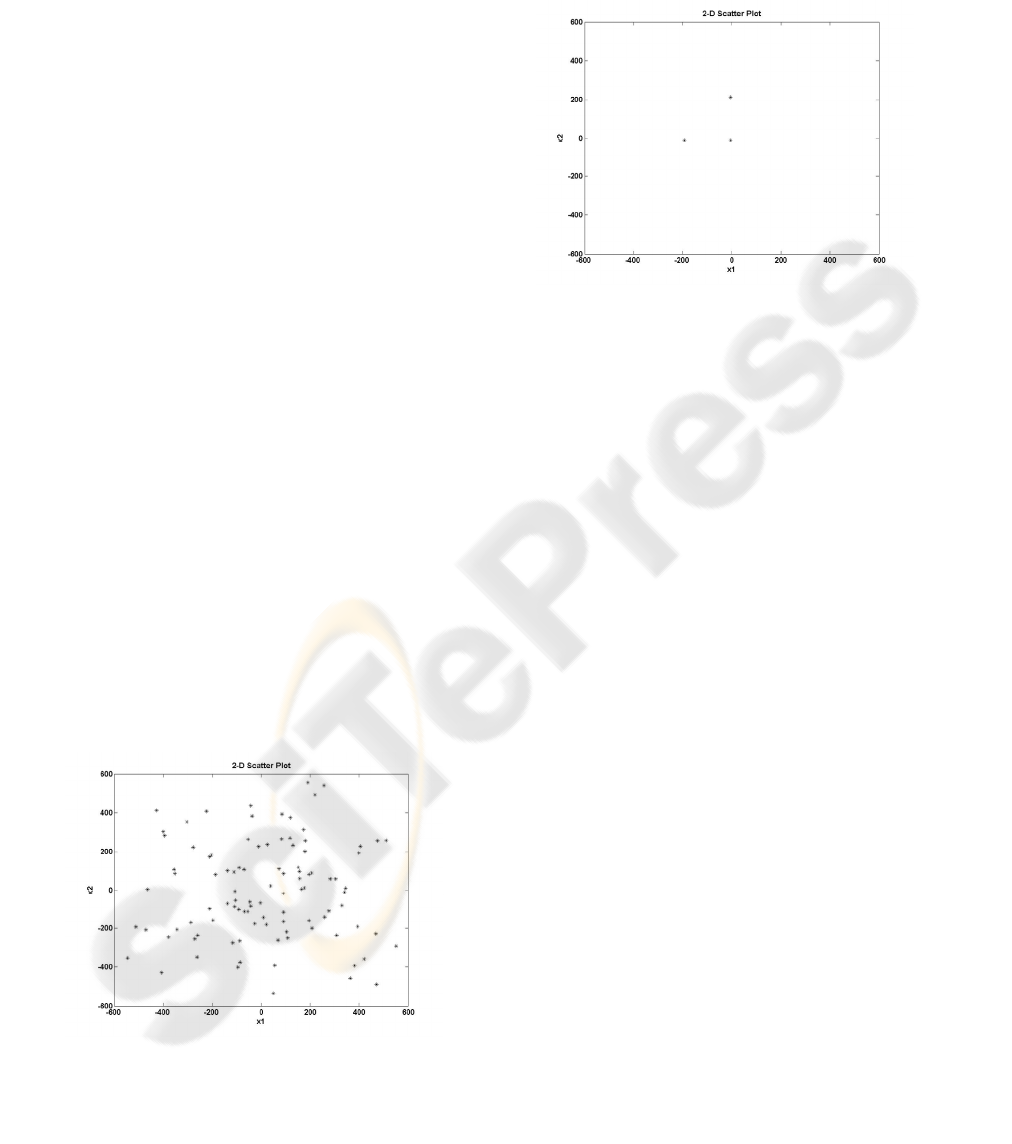
Figure 1: 2-D scatter plot of the initial algorithm’s
population
Assuming that the above figure represents the
location of the initial population of the algorithm,
during the operation of the GA all the chromosomes
tend to converge to the same point of the search
space. As the algorithm converges to an optimum
(global or local), the form of the scatter plot will be
similar to the one of Figure 2.
Figure 2: 2-D scatter plot of the final algorithm’s
population
As can be seen in Figure 2, the diversity of the
final population has significantly decreased over the
generations, since there are only three different
chromosomes. If the solution given by the algorithm
is the global optimum, then the diversity reduction is
acceptable. However, in most of the cases where the
problem to be solved is quite complex, the global
optimum is unknown. It is therefore desirable to
keep the diversity in high levels during the
optimization procedure, in order to explore the
search space as much as possible. Such a strategy
can guarantee the suitability of the current solution,
by high probability.
In the current work, a clustering method is
applied, in order to investigate the location of the
entire population inside the variable space, and the
diversity of the population is measured by means of
the scatter matrices of the resulted chromosome
clusters.
In the next section a brief description of the k-
means clustering algorithm, is taking place, while
the proposed diversity measure is defined, later.
2.1 k-means Algorithm
Clustering methods have many applications in the
engineering science, where data analysis is involved.
In the following, a short definition, of what
clustering stands for, is presented.
Definition 1. Clustering of a given data set, in N-
dimensional space, is the process that partitions
these data into a number of groups (clusters) by
means of a similarity or dissimilarity metric
(Fukunaga, 1990).
AN EXPLORATION MEASURE OF THE DIVERSITY VARIATION IN GENETIC ALGORITHMS
261

One of the most used clustering algorithms is the
k-means one (Looney, 1997), which can be
described in the following steps:
Step 1: Choose K initial cluster centers, C
1
, C
2
… C
k
.
Step 2: Classify each point of the data set to a cluster
according to the following statement: point x
belongs to cluster i
th
with center C
i
, if
jiKji
tCxtCx
ji
≠=∀
−≤−
,,...,2,1,
,)()(
Step 3: Compute the new cluster centers according
to
Kix
N
tC
i
Cx
i
i
,...,2,1,
1
)1( ==+
∑
∈
where N
i
is the number of points belong to the i
th
cluster
.
Step 4: If C
i
(t+1)=C
i
(t), for i=1,2,..,K, then
algorithm is terminated, otherwise goes to step 2.
It must be noted, that the initialization of the
cluster centers, play major role to the performance
and the fast convergent of the algorithm.
In the proposed method, the k-means algorithm
is applied in each generation to cluster the
population chromosomes. In our approach, two
essential assumptions about this algorithm have been
made:
Assumption 1: The initial number K of the cluster
centers are chosen to be equal to the population
size.
Assumption 2: In each iteration of the k-means
algorithm, the empty clusters are being discarded.
Assumption 1 is being justified by Remark 1 of
the next section, while assumption 2 is made to
prevent the increasing of the clusters number, by
keeping the empty ones, which stay empty until the
end of the algorithm.
2.2 Diversity Measure
Once the clustering is applied on each generation of
the GA, a number of clusters are obtained. The
number and the relative location of these clusters
can be used to measure the diversity of the
algorithm.
A high diversity is presented by a population
which covers the search space as much as possible,
while the low diversity is presented by a population
with all chromosomes being the same. These main
concepts can be declared by Remark 1 and 2
respectively, in terms of clustering.
Remark 1: The highest diversity appears when each
chromosome constitutes the center of a cluster with
one member, the chromosome itself and they are
equally spaced, with maximum permit able distance
over the search space (Figure 3).
Remark 2: The lowest diversity appears when all
the chromosomes of the population are the same.
This means that there is one cluster with all the
chromosomes being the center (Figure 4).
Figure 3: 2-D Maximum Diversity, by optimal
chromosomes arrangement
Figure 4: 2-D Minimum Diversity
The above figures correspond to the extreme
situations a GA can be found. In practice, the
algorithm, never presents the diversity illustrated in
Figure 3, but it begins with a random chromosomes
arrangement (Figure 1) and it decreases its diversity
generation by generation. When, the algorithm
terminates, its diversity looks like this of Figure 2, or
this of Figure 4 for full convergence.
To measure these variations of the chromosomes
diversity, the scatter matrices S
w
and S
b
(Fukunaga,
1990), are used, when the clustering has finished.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
262
Between clusters scatter matrix S
b
, describes
how the data clusters, obtained by clustering, are
distributed along the search space, and can be
calculated by using the following equation
()()
∑
=
−−=
K
i
T
iib
mmmmS
1
where K is the number of clusters obtained from k-
means algorithm, m
i
is the mean value of the
chromosomes belong to cluster i, and m the mean
value of the entire population.
Within clusters scatter matrix, S
w
, measures the
distribution of the chromosomes inside the clusters
that they belong, and is described by the equation
()()
T
ij
K
i
N
j
ijw
mChmChS
j
−−=
∑∑
−=11
where N
j
is the number of chromosomes belonging
to the cluster i and Ch
j
the j
th
chromosome. The
remaining symbols are the same as in S
b
.
In the previous equations the quantities are
vectors in
n
ℜ
, according to the problem’s
dimensionality.
Keeping in mind the above definitions of the
scatter matrices, Remark 1 and 2, can be restated as
Remark 3 and 4, below
Remark 3: High diversity occurs when the between
clusters scatter matrix S
b
, takes its optimal value for
a number of clusters equal to the population size,
and simultaneously the within clusters scatter matrix
S
w
, is zero.
Remark 4: Low diversity occurs when the between
clusters scatter matrix S
b
, is zero meaning that the
number of clusters is equal to one, and
simultaneously the within clusters scatter matrix S
w
,
is zero.
Remark 5 is a direct consequent of the above
remarks:
Remark 5: All the intermediate cases are
characterized by random values of S
b
, S
w
and
number of clusters.
In order to represent the situations described by
Remark 1 and 2, by a measurable quantity, the
following measure diversity is introduced.
()
(
)
()()
1log1log +++=
w
N
b
StrStrDiversity
cl
where N
cl
is the number of clusters obtained by the
clustering algorithm and tr() the trace of the matrix .
This measure takes high values as N
cl
and tr(S
b
)
increases, while tr(S
w
) decreases, thus the Remark 3
is satisfied.
The minimum value of this measure appears in
the case presented in Figure 4, and is equal to zero,
since S
b
=0, and S
w
=0.
The above measure has been applied to explore
the diversity of the population, which is being used
to optimize a benchmark function, over the
generations.
The simulations being presented in the next
section, establish the novel diversity measure, a
significant measure to investigate and visualize the
variety of the algorithm population.
3 SIMULATION RESULTS
The experimental results presented here, justify the
usefulness of the proposed diversity measure, in
supervising the progress of a GA.
The previous figures are generated by the
optimization of a known benchmark function, the
Griewangk’s function (Digalakis2000). This
function has the following form for two variables
600600
cos
4000
1
2
1
2
1
2
≤≤−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
∏
∑
=
=
i
i
i
i
i
x
i
xx
f
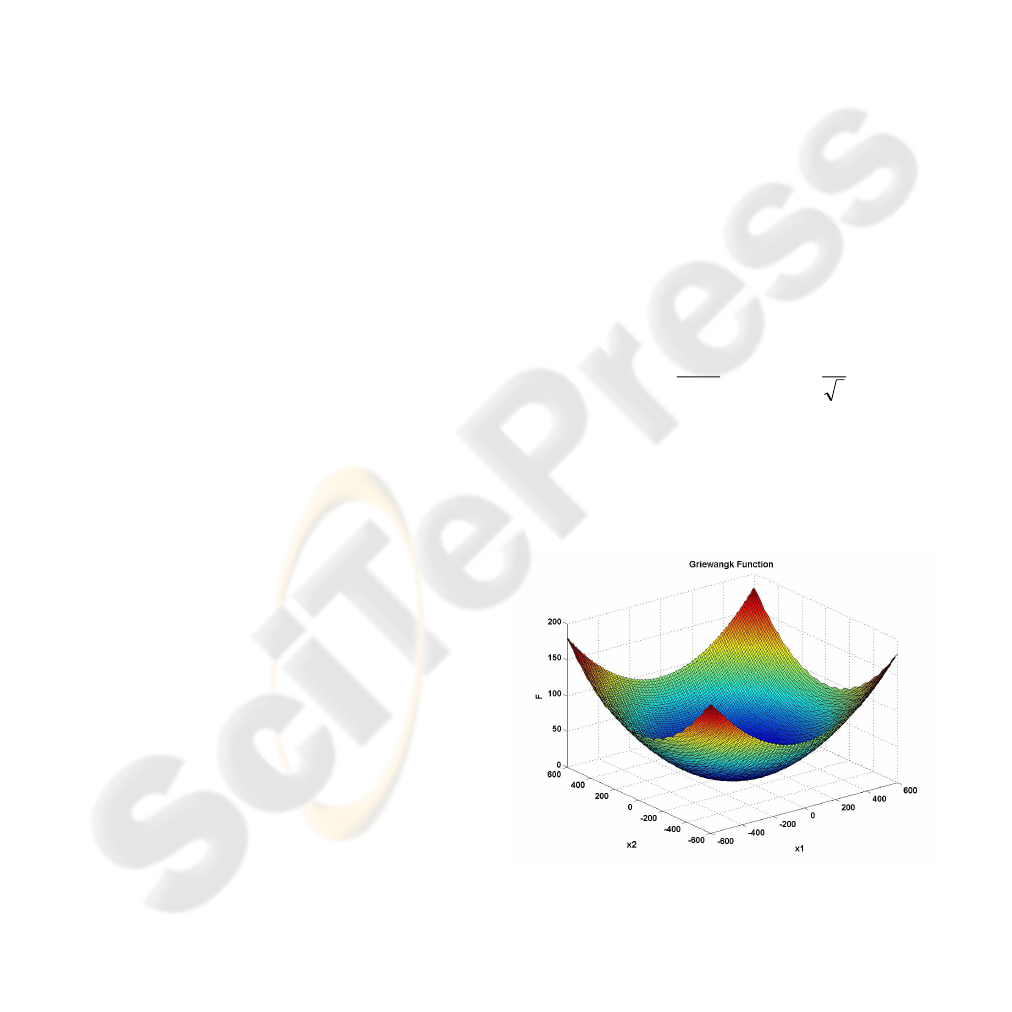
Griewangk’s function is multimodal, but the
location of the minima are regularly distributed, as
illustrated in Figure 5,
Figure 5: Griewangk’s function for 2 dimensions
The algorithm used for these experiments is
configured according to the following Table 1.
AN EXPLORATION MEASURE OF THE DIVERSITY VARIATION IN GENETIC ALGORITHMS
263
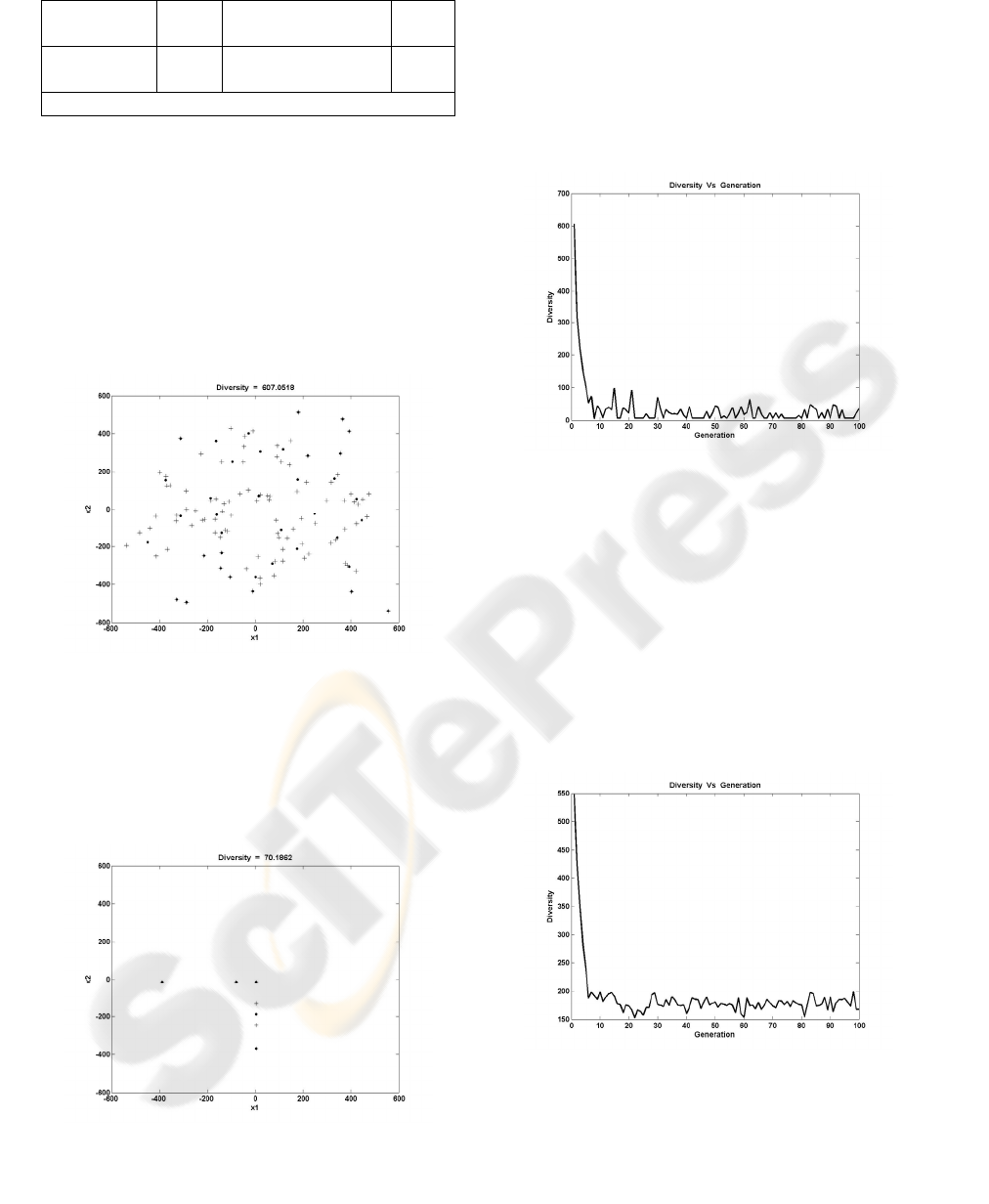
Table 1: GA Parameters
Population
Size
100 Crossover
Probability (P
c
)
0.8
Selection
Method
SUS Mutation
Probability (P
m
)
0.01
Generations 100
The simulations are based on the observations of
the minimization process of the above function,
using a simple real-valued GA. During the
execution, the population diversity in each
generation is measured by using, the previously
introduced formula.
Let us investigate the progress of the GA, in
optimizing the Griewangk’s function. The algorithm
starts with a random population and diversity
measure, as depicted in Figure 6.
Figure 6: Initial population with Diversity = 607.0518
As the above figure shows, the cluster centers
(dots) and the chromosomes (plus signs) cover a
large area of the search space, and thus they provide
high diversity measure.
In Figure 7, the scatter plot of the 30
th
generation’s population is presented.
Figure 7: 30
th
generation’s population Diversity = 70.1862
It is obvious from the above Figures 6-7, that the
diversity of the population has been lost, after 30
generations. If the minimum has been reached, the
goal has been achieved. In the specific case, the
minimum after 30 generations is 0.5115, quite far
from the global minimum, which is 0.
Thus, the measured diversity can be useful in
changing the crossover and mutation probabilities, in
order to converge to the global minimum.
Figure 8, shows the variation of the diversity
through the generations
Figure 8: Diversity variation of the algorithm (Pm=0.01)
For the rest of the generations, the diversity is
varied in low levels, decreasing the probability to
find the global optimum. If the diversity stays in
high levels this probability is increased.
Therefore, the diversity measure proposed in this
paper seems to have the ability to describe the
evolution of the algorithm’s population.
It is very interesting to investigate, the behaviour
of the algorithm in terms of the diversity, by
changing the crossover and mutation probabilities P
c
and P
m
, respectively.
Figure 9, presents the diversity variation, for
P
m
=0.1.
Figure 9: Diversity variation of the algorithm (P
m
=0.1)
Mutation probability (P
m
) controls the
appearance of the search space points that might
have not been presented before. In other words, it
manages to generate all the possible search space
points, by some probability. Thus, it tries to keep the
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
264

diversity in high levels, a fact that is proved by the
form of the diversity variation of Figure 9. As, can
be seen from this figure, the diversity fluctuates
between 100 and 200, while in the case of P
m
=0.01,
it varies between 5 and 50.
On the other hand, crossover probability (P
c
),
defines the probability by which the chromosomes
interchange their information, in order to produce
better individuals. This probability is changed to 0.5,
in the initial algorithm and the measured diversity is
drawing in Figure 10
.
Figure 10: Diversity variation of the algorithm (P
c
=0.5)
Crossover probability determines the population
diversity, by a high degree, as displayed in Figure
10, since a reduction of the crossover probability has
led to premature convergence.
It must be noted that, each one of these
experiments is executed for 100 times, and the mean
diversity has been presented in the above figures.
Additionally, Figures 9 and 10 have been obtained
by applying only one of the operators (crossover,
mutation) each time, during the algorithm execution.
These simulations demonstrates, that the
behaviour of the GA and the impact the crossover
and mutation probabilities have, can be represented
by the diversity measure introduced in this paper.
4 CONCLUSIONS
An innovative formula, which measures the diversity
of GA’s population, has been introduced in the
previous sections. The diversity measure is based on
the statistical quantities that describe the
chromosome clusters obtained by applying the k-
means algorithm to the chromosomes population
.
The resulted measurement can be used to
calibrate the GA by choosing the appropriate
crossover P
c
and mutation P
m
probabilities.
Additionally this measurement will be useful in
adjusting the probabilities on-line during the
execution of the algorithm, in order to keep the
diversity in high levels.
Appropriate experiments have shown that the
proposed measure describes the evolution of the
algorithm’s population. This measure can also be
used to any population-based algorithm, since it uses
the statistical properties of the population’s
distribution over the search space.
Future work must be carried out in order to use
this measure to adaptively adjust the crossover and
mutation probabilities. Additional experiments with
more complex optimization problems such as Neural
Networks training by using GAs must be done. The
training phase of a Neural Network is a process that
is quite blind, because the only measure that one
may have is the approximation error, and due to the
high dimensionality the investigation of the weights
evolution is not possible.
REFERENCES
Bandyopadhyay, S., Murthy, C.A., Pal, S.K., 1995,
Pattern Classification with Genetic Algorithms,
Pattern Recognition Letters, (16), pp. 801-808.
Digalakis, J.G., Margaritis, K.G., 2000, On Benchmarking
Functions for Genetic Algorithms, Int. Journal
Computer Math., Vol.00, pp. 1-27.
Fukunaga, K., 1990, Introduction to Statistical Pattern
Recognition, 2
nd
edition, Academic Press.
Holland, J.H., 2001, Adaptation in Natural and Artificial
Systems, 6
th
edition, MIT Press.
Jamshidi, M., Coelho, L.S., Krohling, R.A., Fleming, P.J.,
2003. Robust Control Systems with Genetic
Algorithms, CRC Press.
Looney, C.G., 1997, Pattern Recognition using Neural
Networks, Theory and Algorithms for Engineers and
Scientists, Oxford University Press.
Mirmehdi, M., Palmer, P.L., Kittler, J.,1997, Genetic
Optimisation of the Image Feature Extraction Process,
Pattern Recognition Letters (18), pp. 355-365.
Mitchell, M., 2002, An Introduction to Genetic
Algorithms, 8
th
edition, MIT Press.
Papakostas, G.A., Kosmidou, O.I., Antonakis, I.E., 2004,
An LMI-Based Genetic Algorithm For Guaranteed
Cost Control, 1
st
International Conference on
Informatics in Control, Automation and Robotics
(ICINCO’04), Setubal, Portugal
Papakostas, G.A., Boutalis Y.S., Mertzios B.G., 2003,
Evolutionary Selection of Zernike Moment Sets in
Image Processing, 10
th
International Workshop on
Systems, Signals and Image Processing (IWSSIP’03),
Prague, Czech Republic.
AN EXPLORATION MEASURE OF THE DIVERSITY VARIATION IN GENETIC ALGORITHMS
265
